Similar presentations:
Моделирование параметров и процессов технологических машин
1.
Дисциплина«МОДЕЛИРОВАНИЕ ПАРАМЕТРОВ И
ПРОЦЕССОВ ТЕХНОЛОГИЧЕСКИХ
МАШИН»
Разработал: профессор, д.т.н. Мясищев Д.Г.
2.
Рекомендуемая литература1. Основные источники:
1. Александров В.А., Александров А.В. Моделирование технологических
процессов лесных машин: Учебник для вузов / СПб.: ГЛТА, 2009. – 297 с.
2. Мясищев Д.Г. Моделирование и оптимизация параметров компонентов лесных
машин: учебное пособие / Архангельск, ИД САФУ, 2014. – 104 с.
3. Мясищев Д.Г. Статистическая динамика машин и оборудования лесного
комплекса (в примерах): учебное пособие / Д.Г.Мясищев; Сев. (Арктич.) федер. Ун-т им.
М.В.Ломоносова. - Архангельск: САФУ, 2017. – 115 с.
2. Дополнительные источники:
1.
Александров В.А., Александров А.В. Вибронагруженность операторов
валочно-пакетирующих машин / СПб.: ГЛТУ, 2017. – 317 с.
2. Гоберман В.А., Гоберман Л.Н. Технология научных исследований – методы,
модели, оценки: учебное пособие. 2-е изд. Стереотипное. – М.: МГУЛ, 2002. – 390 с.
3. Питухин А.В., Шиловский В.Н., Костюкевич В.М. Надежность
лесозаготовительных машин и оборудования: Учебное пособие. - СПб.: Издательство
«Лань», 2010, - 288 с.
3.
ЛЕКЦИЯ №1Тема: Цель дисциплины, предмет ее
изучения. Классификация методов
моделирования.
4.
Цель дисциплины и ее предметполучить
элементарные
знания
и
навыки,
компетентность
в
рассматриваемом предмете, - процессе нахождения наиболее эффективных
(оптимальных)
условий,
образов
действия
и
значений
конкретных
параметров с учетом выбранных ограничений, а именно:
адекватно определить проблему в понятиях, составляющих ее суть, то
есть сформулировать проблему, к решению которой приступают;
трансформировать решаемую задачу с языка физических и технических
терминов на язык математики;
найти искомое решение аналитически;
осуществить анализ найденного решения с точки зрения его возможной
практической реализации.
5.
Определение моделирования• Моделированием называется исследование на специальных объектах
(например: материальных – экспериментальный образец, модель
машины и пр. и идеальных – математическая модель в виде
дифференциальных уравнений, регрессионная зависимость и пр.),
называемых моделями, различных процессов, явлений или свойств
реальной действительности. При этом моделью называется некоторый
нетождественный исследуемому объекту аналог, но заменяющий его
по основным свойствам, процессам. Модель всегда выполняется в
форме, диктуемой конкретной задачей исследования, свойствами
реального объекта, имеющимися материальными средствами для
исследования.
6.
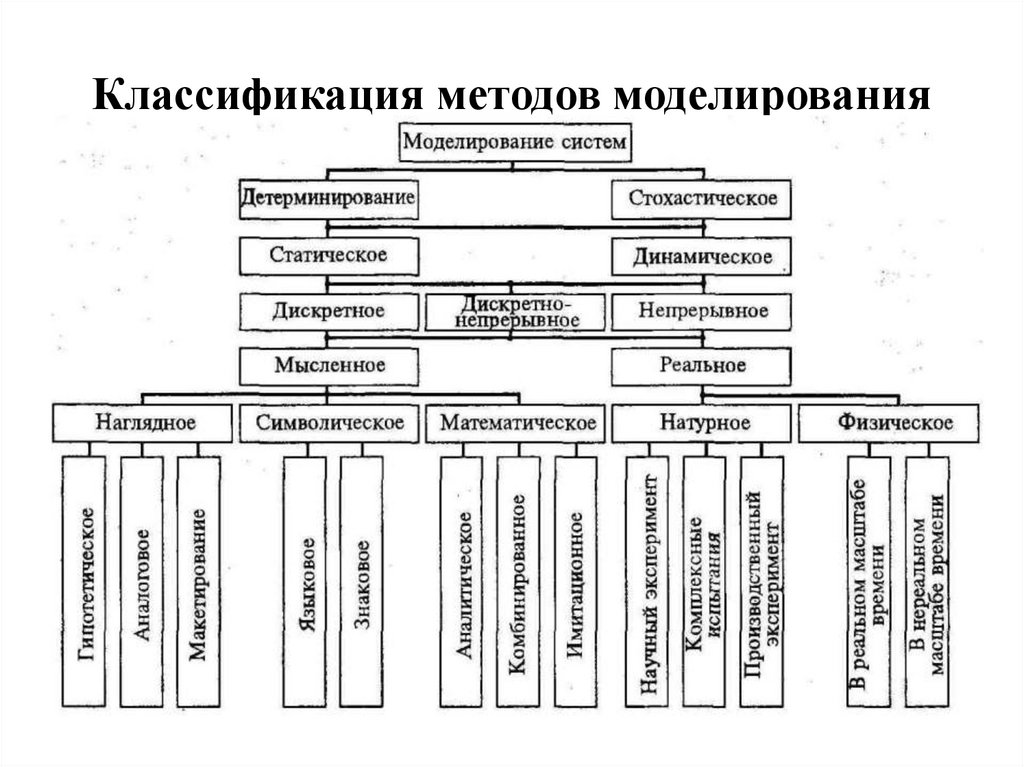
Классификация методов моделирования7.
Наиболее характерные видымоделирования
• Натурное моделирование – как разновидность
экспериментальных
исследований,
предполагает
исследование
действующем
объекте
специально
на
разработанной
по
программе,
отличающейся от режима обычного нормального
функционирования. Его важная роль быть “судьей”
между теорией и практикой, но и быть “донором”
для теории.
8.
Наиболее характерные видымоделирования
• Математическое
универсальный,
моделирование
гибкий
и
наиболее
перспективный
метод
исследования.
• Математической
моделью
объекта
называется
изображение с помощью различных математических
средств наиболее существенных на данном этапе
исследования сторон объекта и выраженных в удобной
для исследования форме.
9.
Наиболее характерные видымоделирования
• Физическое моделирование – предполагает
использование теории подобия и основано на
исследовании специальной модели, имеющей
ту же физическую природу, что и сложный
исследуемый объект.
Метод
широко
применяется в авиации, судостроении и др.,
для технологической техники не характерно.
10.
ЛЕКЦИЯ №2Тема:. Принципы построения
математических моделей.
11.
Математическое моделирование имеетдостоинства:
А) использование однотипных
математических моделей для исследования
систем и процессов с разным физическим
содержанием;
Б) не требуется всеобъемлющей информации
о проектируемом объекте;
В) возможность заменить натурные
исследования и физическое моделирование,
т.е. уменьшить затраты.
12.
Пример схемы для математической модели1) эквивалентная схема одно
массовой упругой системы
13.
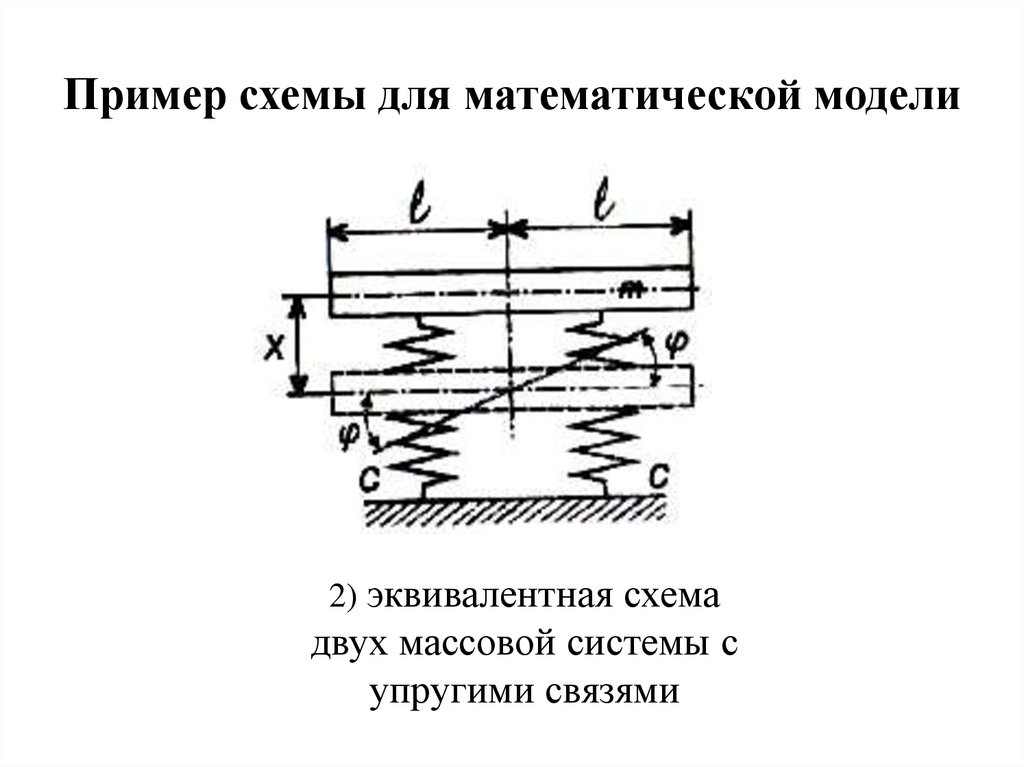
Пример схемы для математической модели2) эквивалентная схема
двух массовой системы с
упругими связями
14.
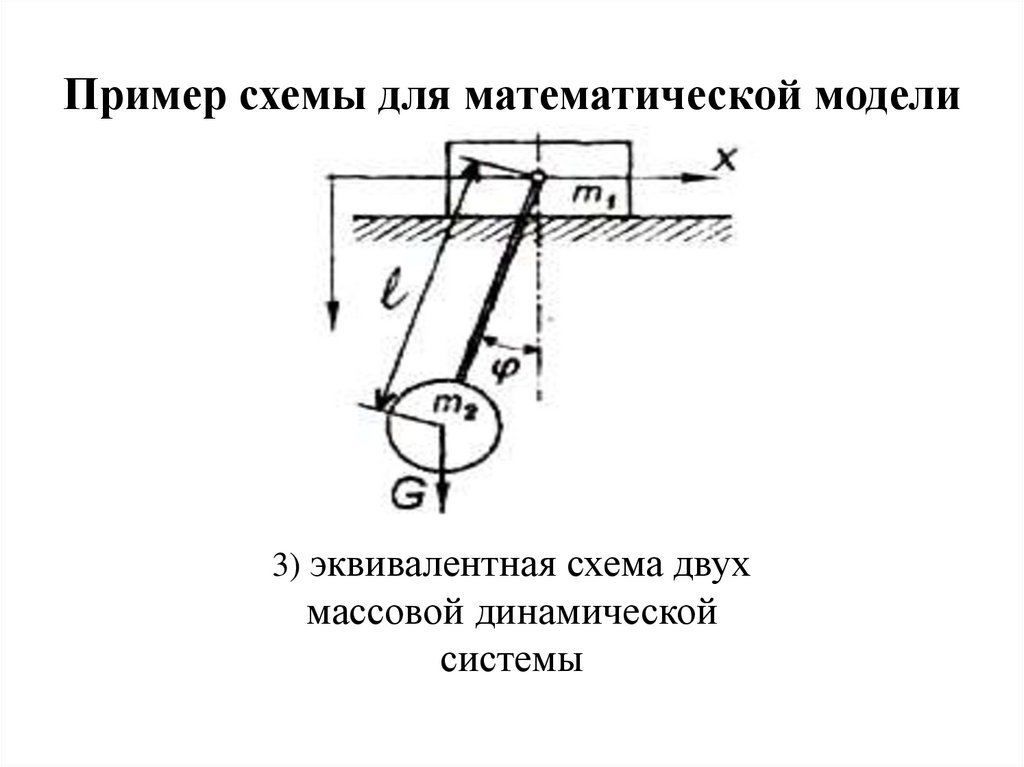
Пример схемы для математической модели3) эквивалентная схема двух
массовой динамической
системы
15.
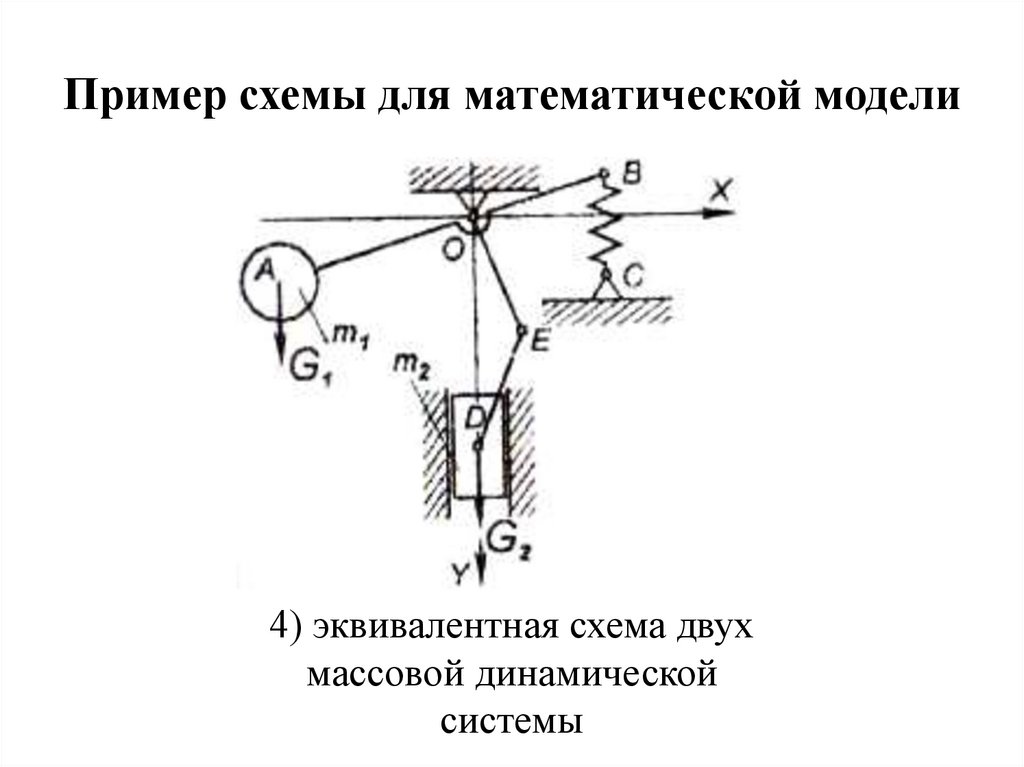
Пример схемы для математической модели4) эквивалентная схема двух
массовой динамической
системы
16.
Пример схемы для математической модели5) эквивалентная схема одно
массовой динамической
системы на двойном
упругом основании
17.
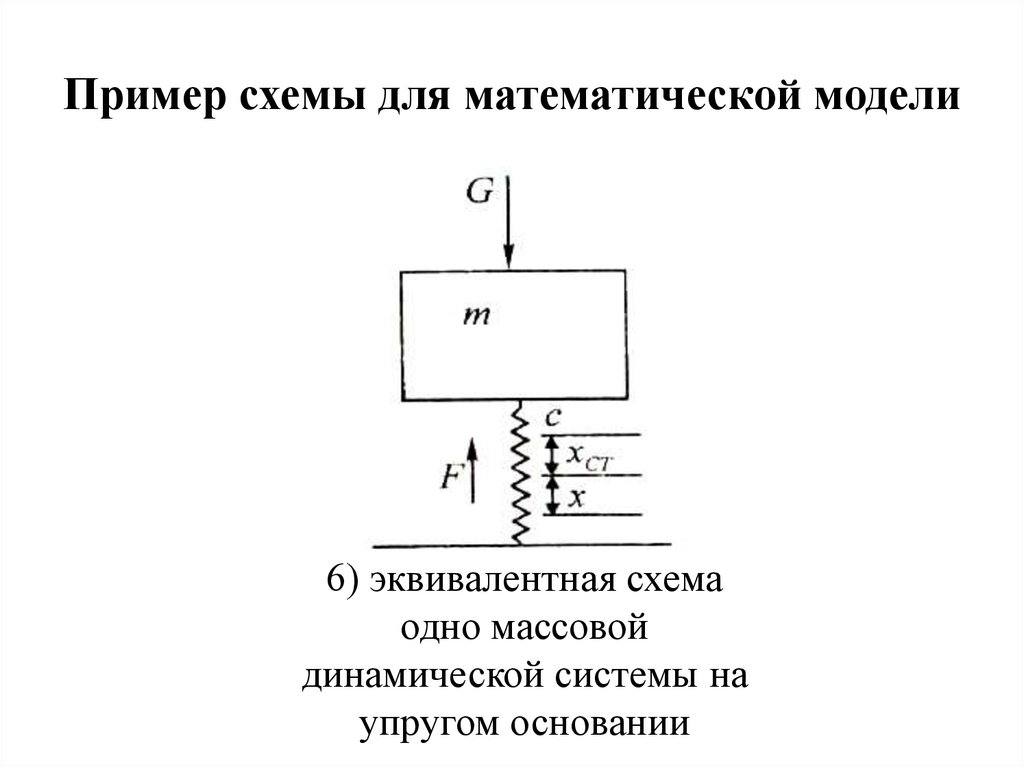
Пример схемы для математической модели6) эквивалентная схема
одно массовой
динамической системы на
упругом основании
18.
Эквивалентные преобразования систем ипроцессов
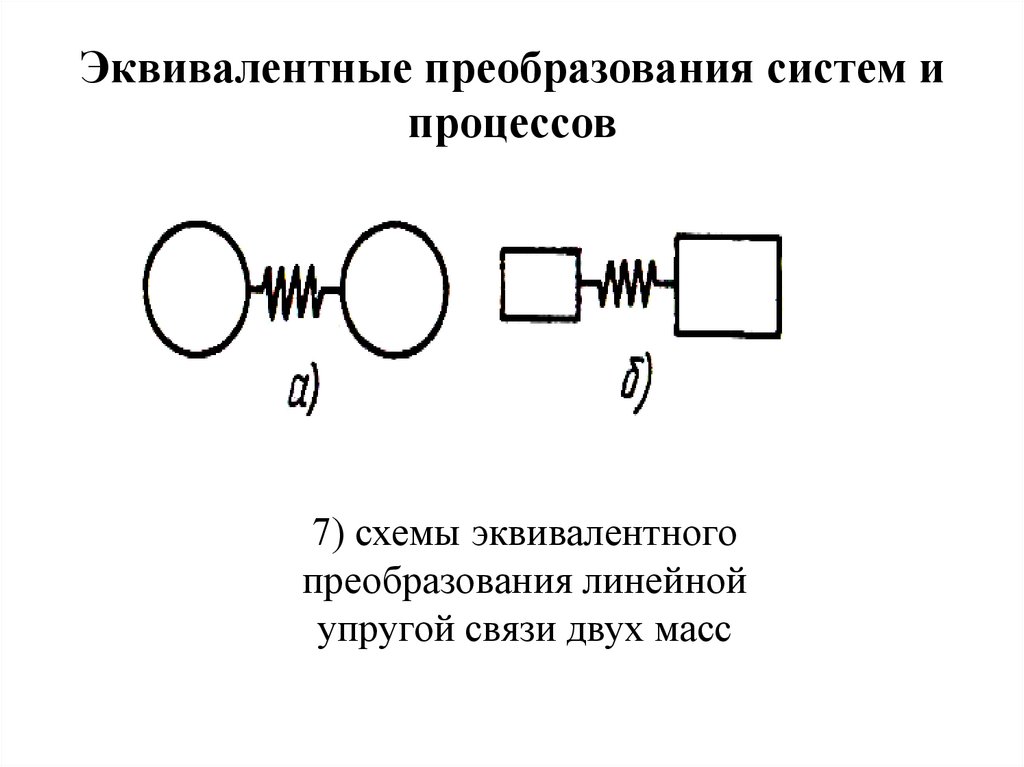
7) схемы эквивалентного
преобразования линейной
упругой связи двух масс
19.
Эквивалентные преобразования систем ипроцессов
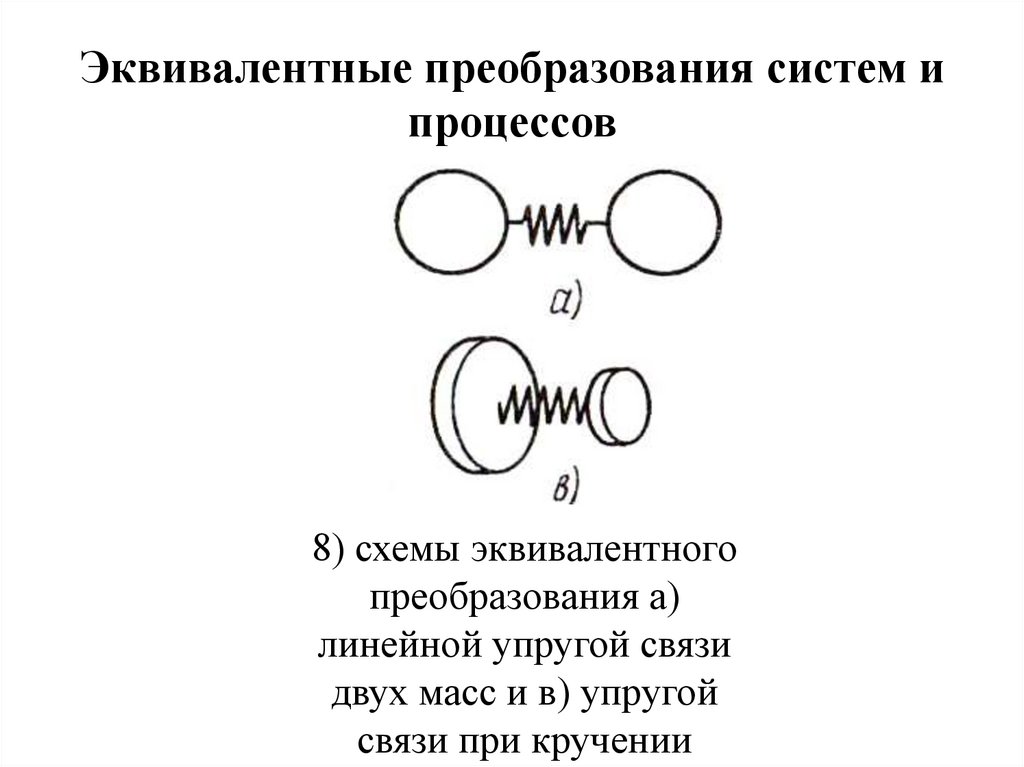
8) схемы эквивалентного
преобразования а)
линейной упругой связи
двух масс и в) упругой
связи при кручении
20.
Эквивалентные преобразования систем ипроцессов
9)схемы эквивалентного
преобразования б) линейной
упругой связи двух масс и г)
упругой связи при кручении
21.
Эквивалентные преобразования систем ипроцессов
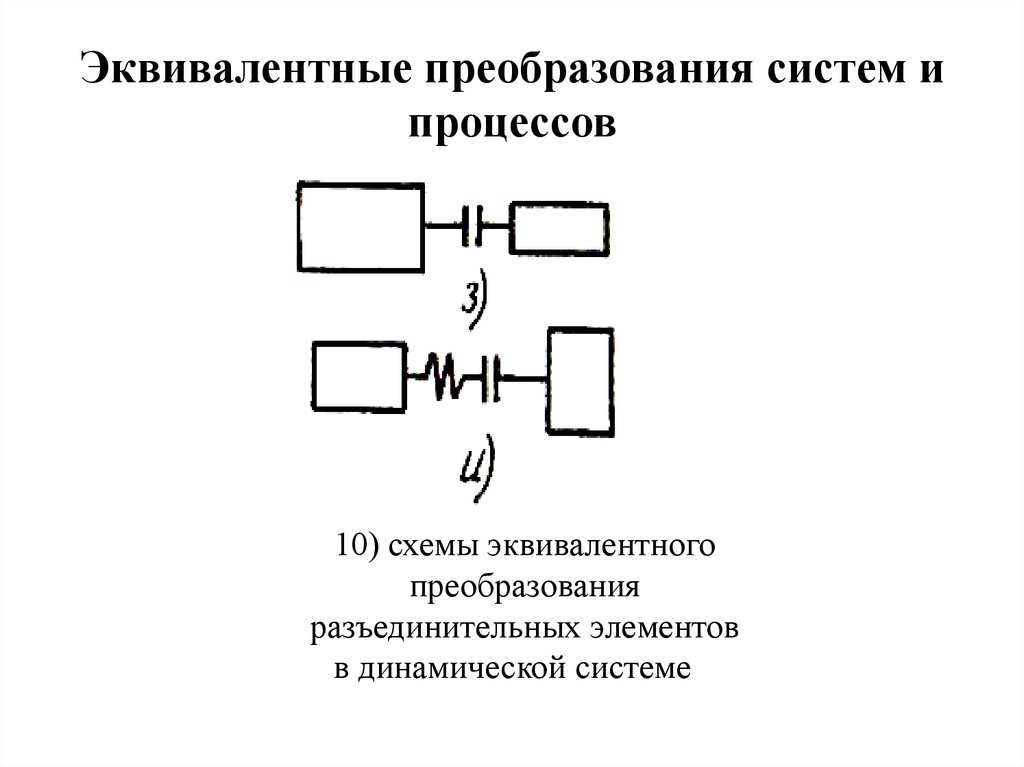
10) схемы эквивалентного
преобразования
разъединительных элементов
в динамической системе
22.
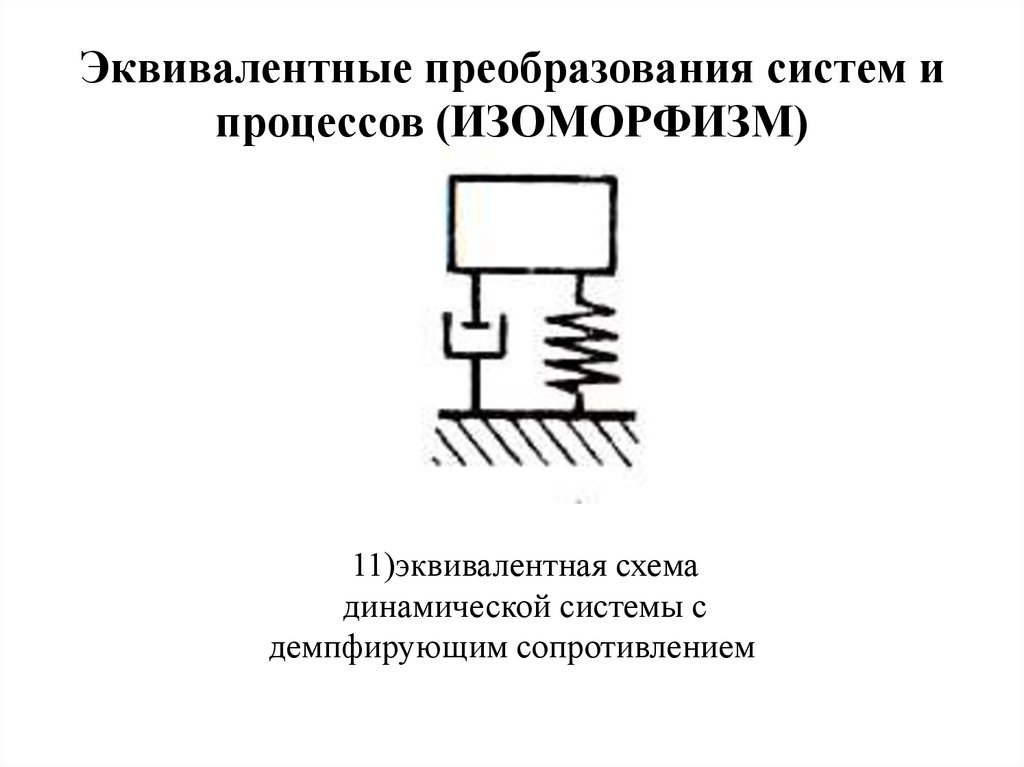
Эквивалентные преобразования систем ипроцессов (ИЗОМОРФИЗМ)
11)эквивалентная схема
динамической системы с
демпфирующим сопротивлением
23.
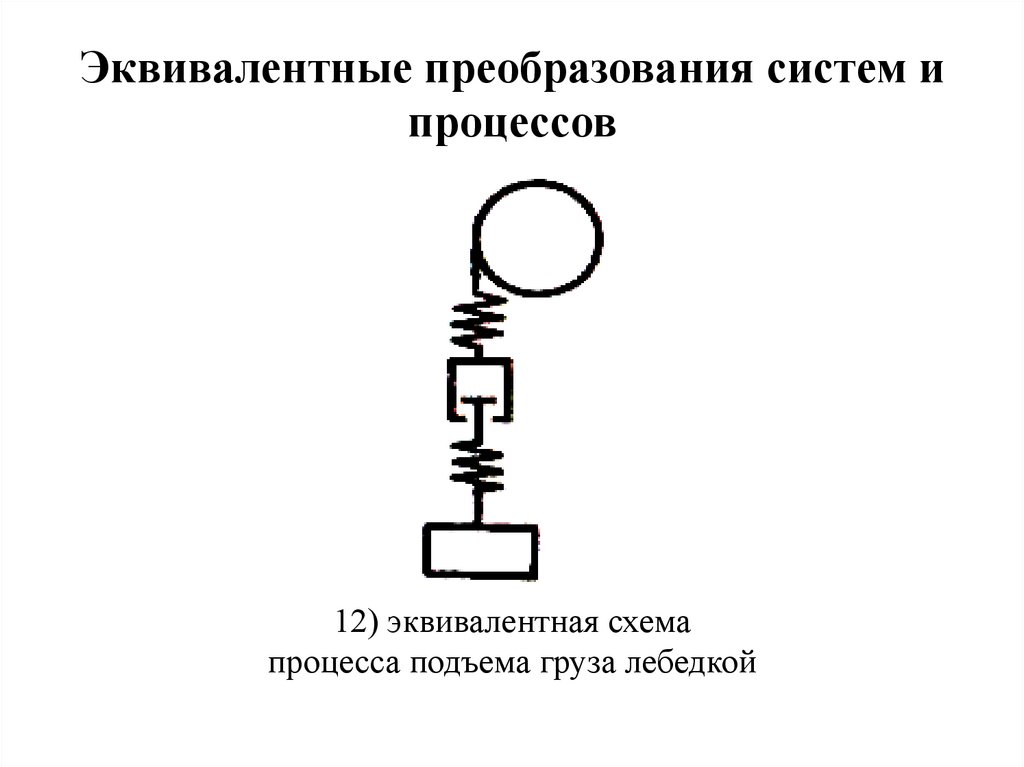
Эквивалентные преобразования систем ипроцессов
12) эквивалентная схема
процесса подъема груза лебедкой
24.
Определение приведенных параметровдинамических систем в механике
13) уравнение
приведения силы
14) уравнение приведения
момента
25.
Определение приведенных параметровдинамических систем в механике
15) уравнения баланса
кинетической энергии системы
26.
Определение приведенных параметровдинамических систем в механике
16) уравнение приведения массы
27.
Определение приведенных параметровдинамических систем в механике
17) уравнение приведения момента инерции
28.
Определение приведенных параметровдинамических систем в механике
18) уравнение приведения
жесткости ведущего элемента
динамической системы к
ведомому элементу при силовом
режиме функционирования
29.
Определение приведенных параметровдинамических систем в механике
19) уравнение приведения
жесткости ведомого элемента
динамической системы к
ведущему элементу при силовом
режиме функционирования
30.
Определение приведенных параметровдинамических систем в механике
20) суммарная приведенная
жесткость при последовательном
соединении упругих элементов
31.
Определение приведенных параметровдинамических систем в механике
21) суммарная приведенная
жесткость при параллельном
соединении упругих элементов
32.
Определение приведенных параметровдинамических систем в механике
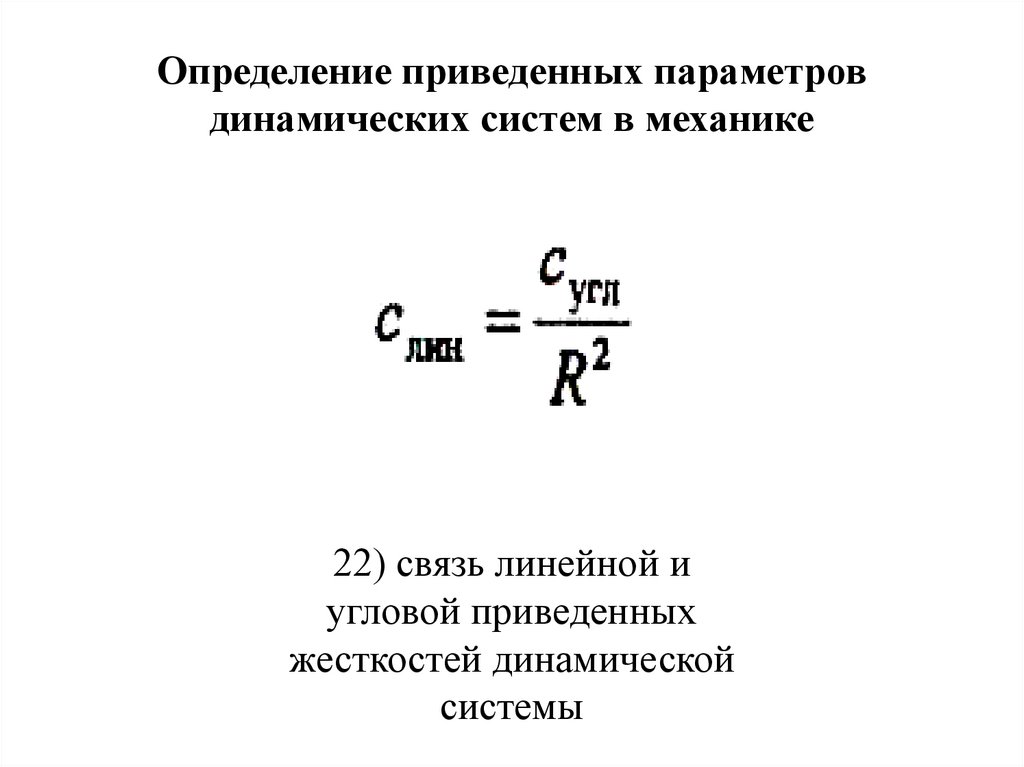
22) связь линейной и
угловой приведенных
жесткостей динамической
системы
33.
Определение приведенных параметровдинамических систем в механике
23) баланс демпфирования
силовой динамической
системы
34.
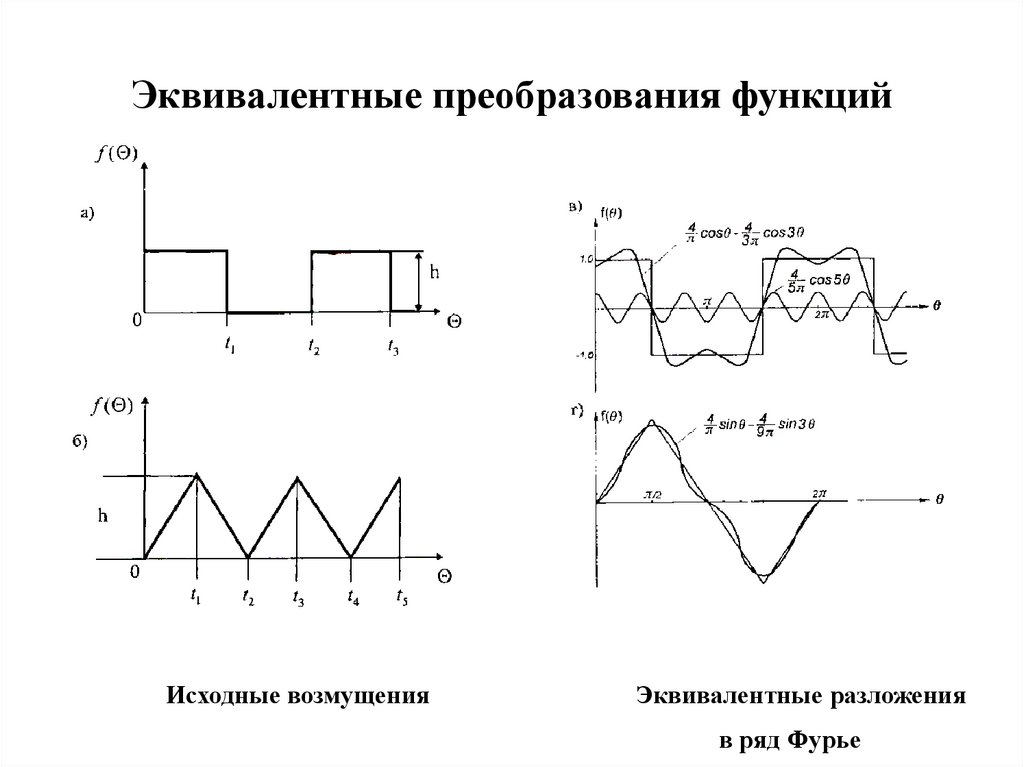
Эквивалентные преобразования функцийИсходные возмущения
Эквивалентные разложения
в ряд Фурье
35.
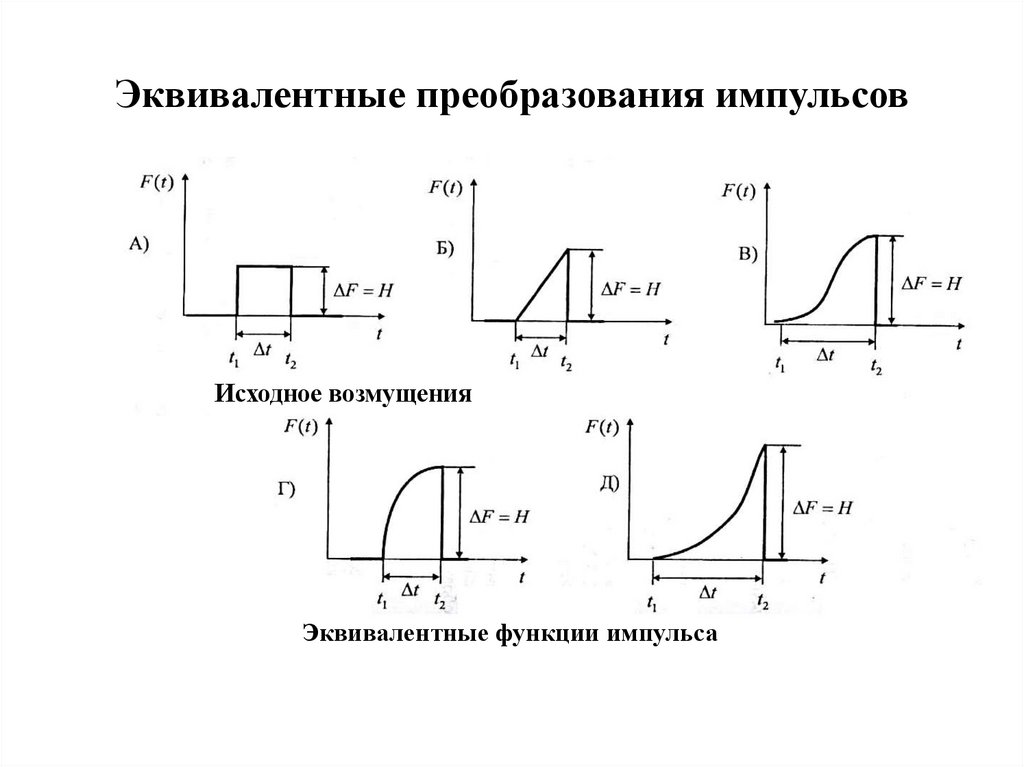
Эквивалентные преобразования импульсовИсходное возмущения
Эквивалентные функции импульса
36.
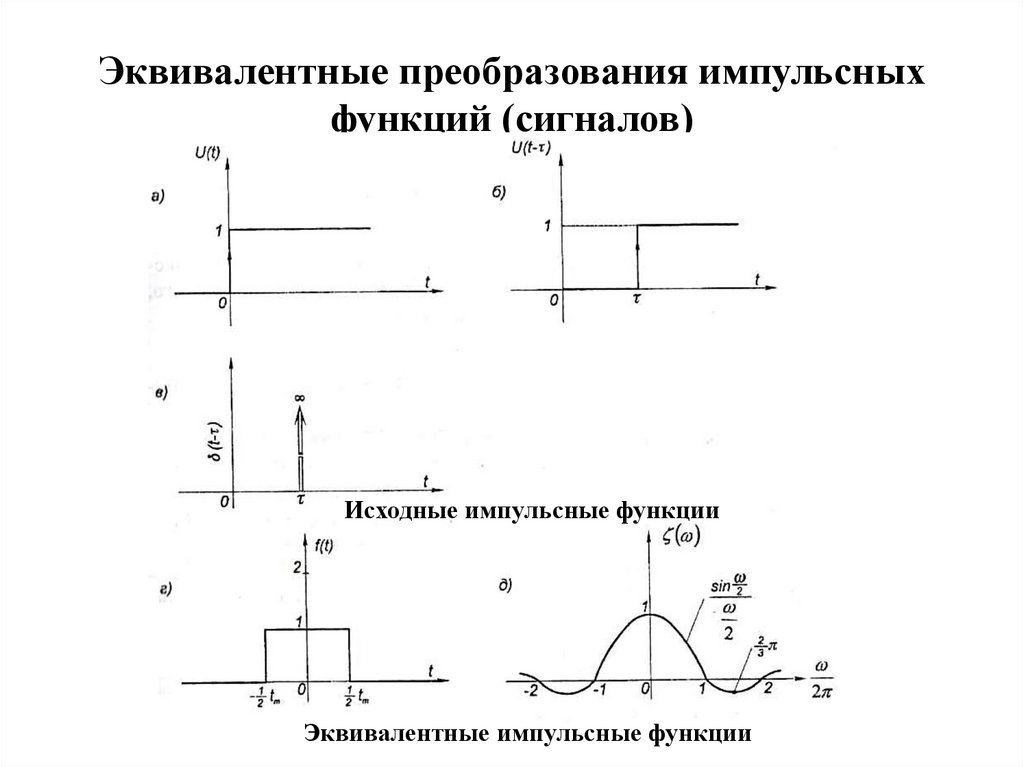
Эквивалентные преобразования импульсныхфункций (сигналов)
Исходные импульсные функции
Эквивалентные импульсные функции
37.
Математическое условие изоморфизма вэквивалентных преобразованиях
Если на входе системы действует величина X1, а на
выходе системы ей соответствует величина Y1, то при
замене X1 эквивалентной ей величиной X2,
соответствующая выходная величина Y2 должна быть
приблизительно равна величине Y1.
38.
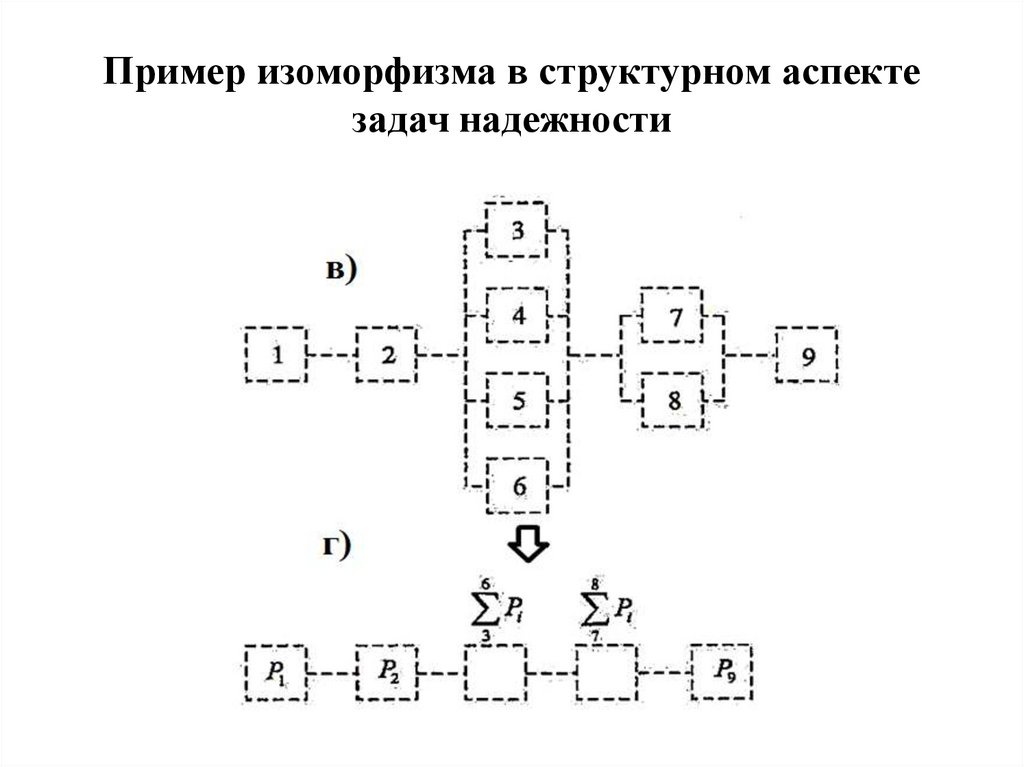
Пример изоморфизма в структурном аспектезадач надежности
39.
Пример изоморфизма в структурном аспекте задачнадежности (математическая интерпретация)
40.
ЛЕКЦИЯ № 3Тема:Построение математических моделей
механических систем
• математическое
моделирование
на
основе
обыкновенных дифференциальных уравнений;
• математическое
моделирование
передаточных функций;
в
виде
• математическое моделирование в виде параметров
функций случайных процессов
41.
Системы координат и связи в оценке динамикимеханических объектов
Величины, при помощи которых определяется положение
данной точки относительно другой токи, взятой за начало
отсчета, называют координатами (системами отсчета).
Неподвижную систему координат, связанную с землей,
называют инерционной системой координат.
Подвижные системы координат связывают с исследуемым
объектом и считают “вмороженным” в его тело, двигаясь
вместе с ним.
При рассмотрении динамических систем, совершающих
сложное движение, обычно применяют как неподвижные.
так и подвижные системы координат.
42.
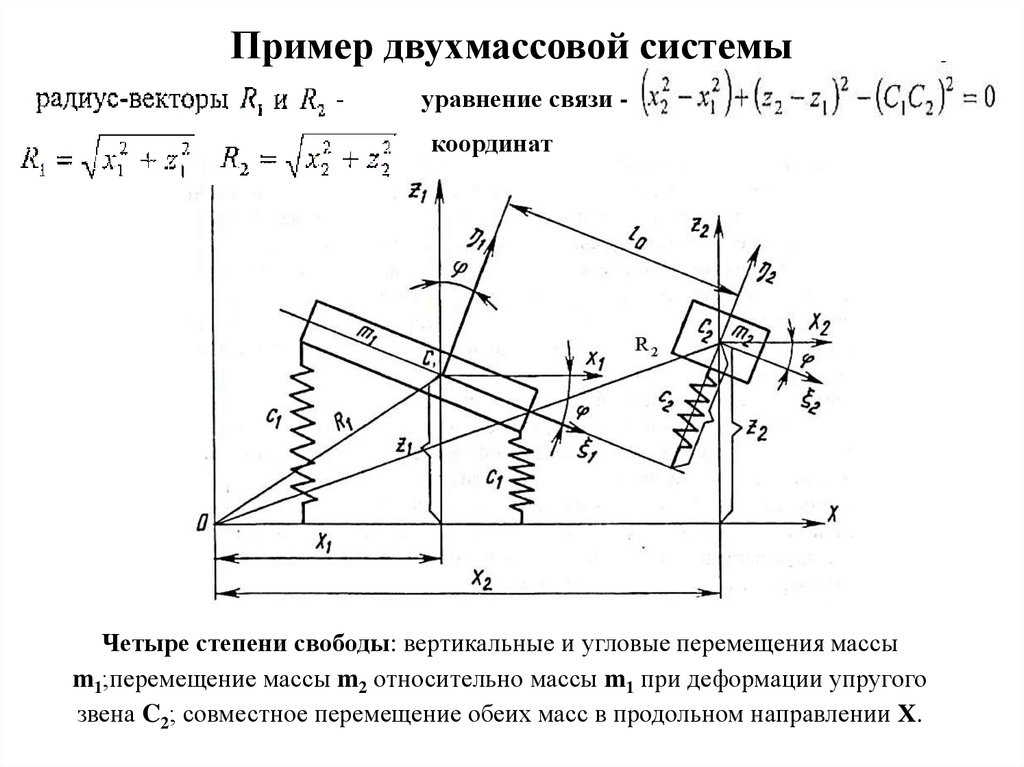
Пример двухмассовой системы-
уравнение связи координат
Четыре степени свободы: вертикальные и угловые перемещения массы
m1;перемещение массы m2 относительно массы m1 при деформации упругого
звена C2; совместное перемещение обеих масс в продольном направлении Х.
43.
Пример двухмассовой системы44.
Понятие связи в механических системах( голономные, неголономные -)
i – порядковый номер уравнения связи, n – число точек системы
45.
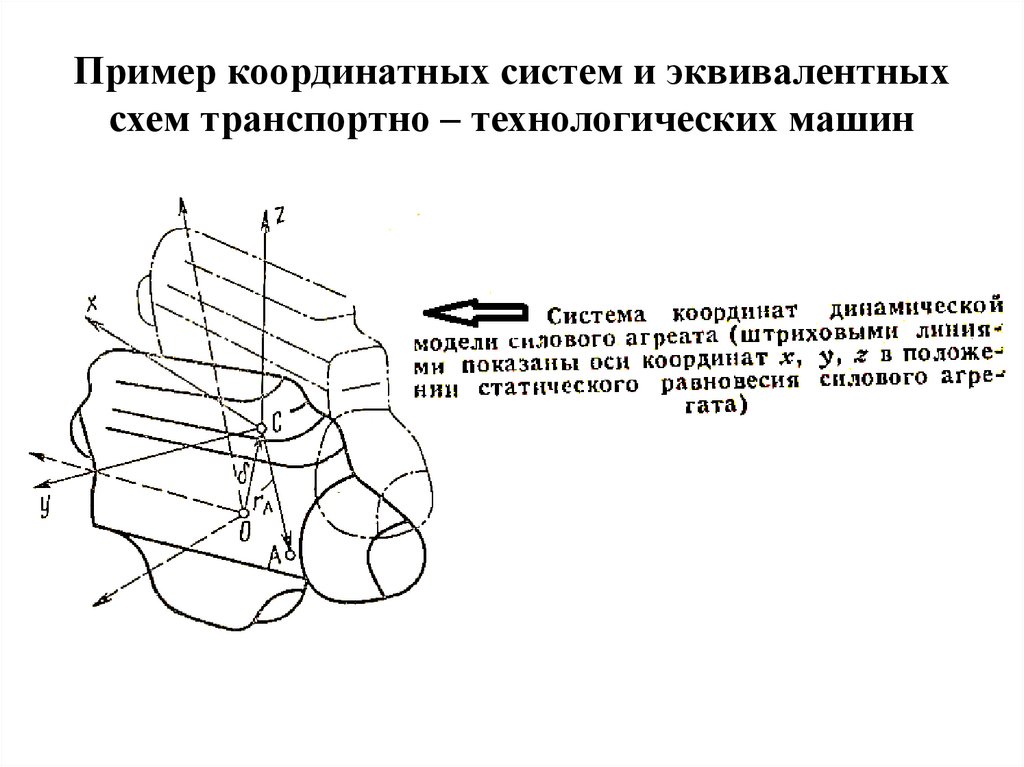
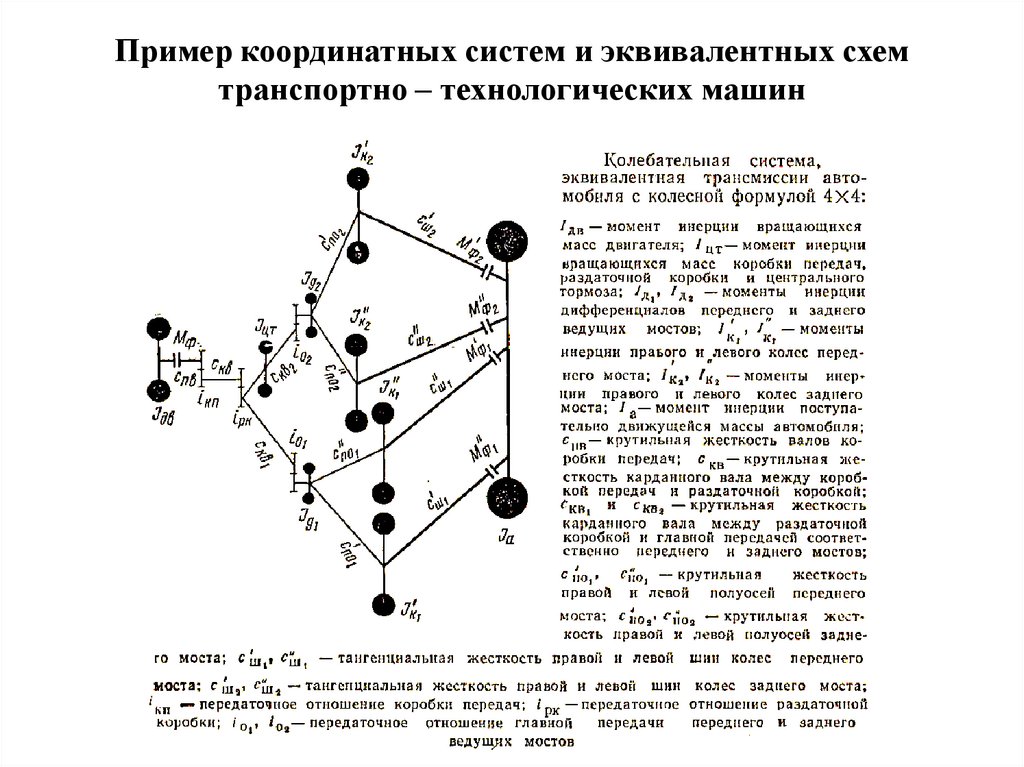
Пример координатных систем и эквивалентныхсхем транспортно – технологических машин
46.
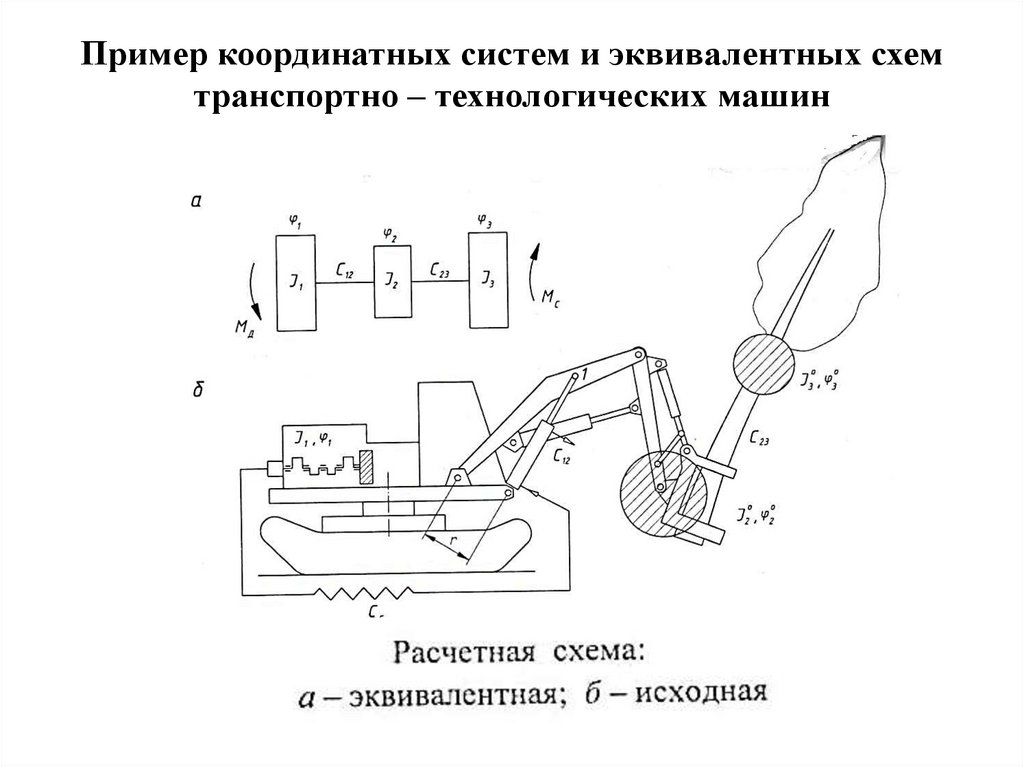
Пример координатных систем и эквивалентныхсхем транспортно – технологических машин
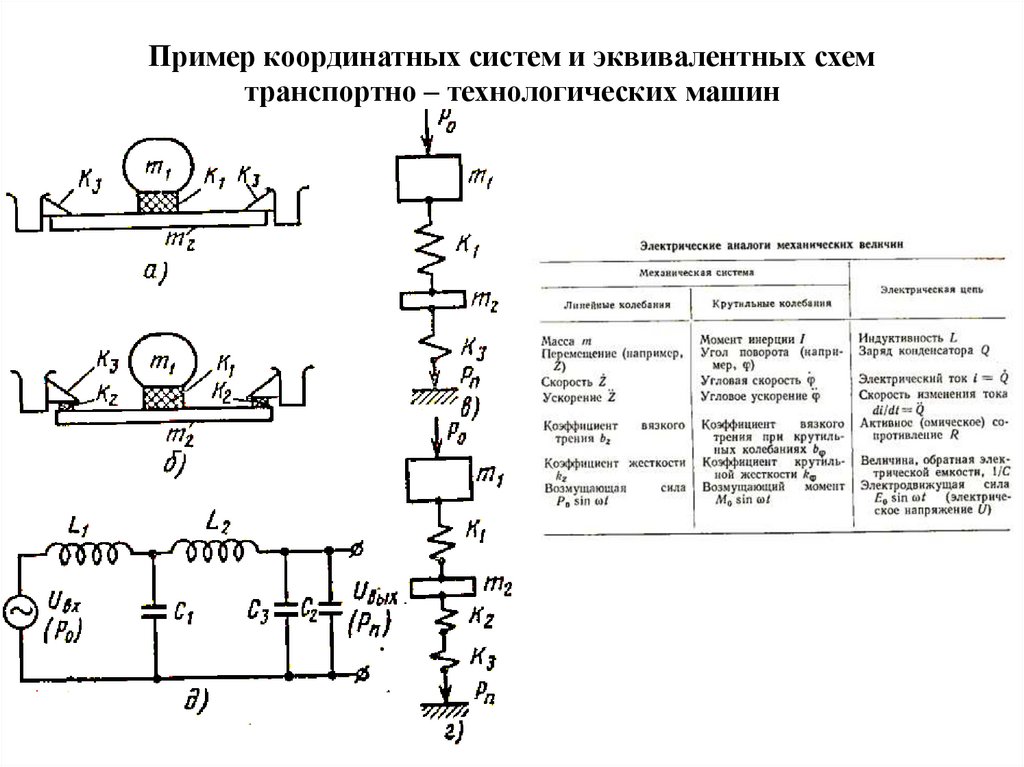
47.
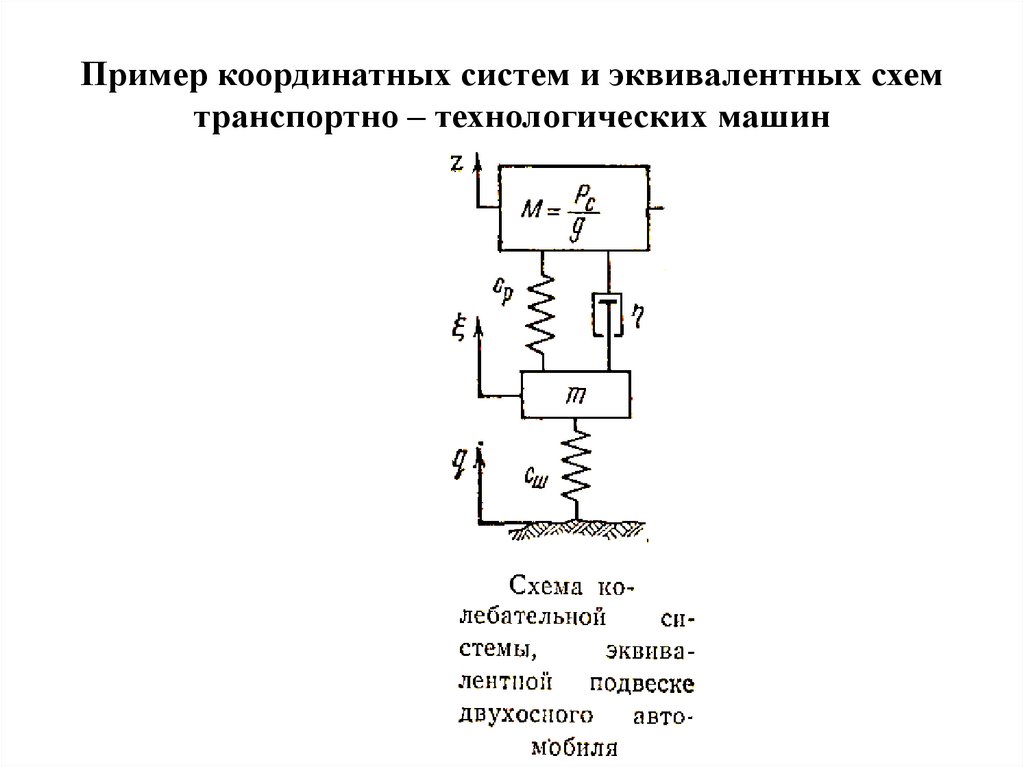
Пример координатных систем и эквивалентных схемтранспортно – технологических машин
48.
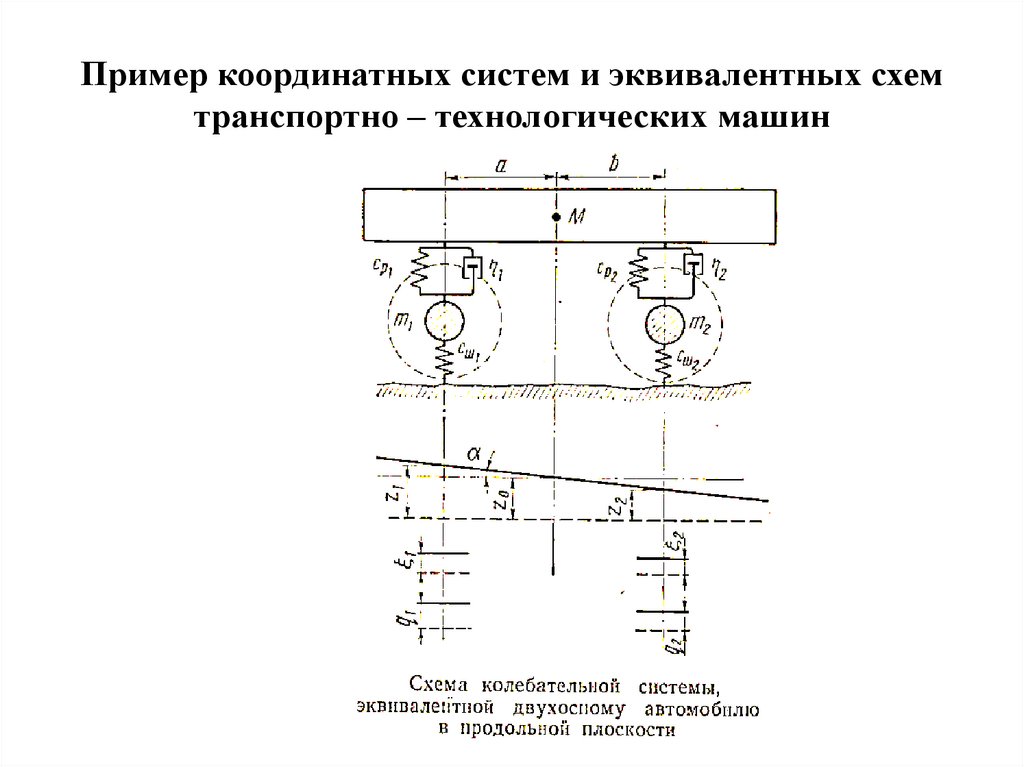
Пример координатных систем и эквивалентных схемтранспортно – технологических машин
49.
Пример координатных систем и эквивалентных схемтранспортно – технологических машин
50.
Пример координатных систем и эквивалентных схемтранспортно – технологических машин
51.
Пример координатных систем и эквивалентных схемтранспортно – технологических машин
52.
Виртуальные (возможные) перемещения приматематическом моделировании динамики
механических систем
53.
Виртуальные (возможные) перемещения приматематическом моделировании динамики механических
систем
54.
55.
Основные уравнения моделирования динамикимеханических систем (принцип Даламбера,
общее уравнение динамики, уравнения Лагранжа
второго рода)
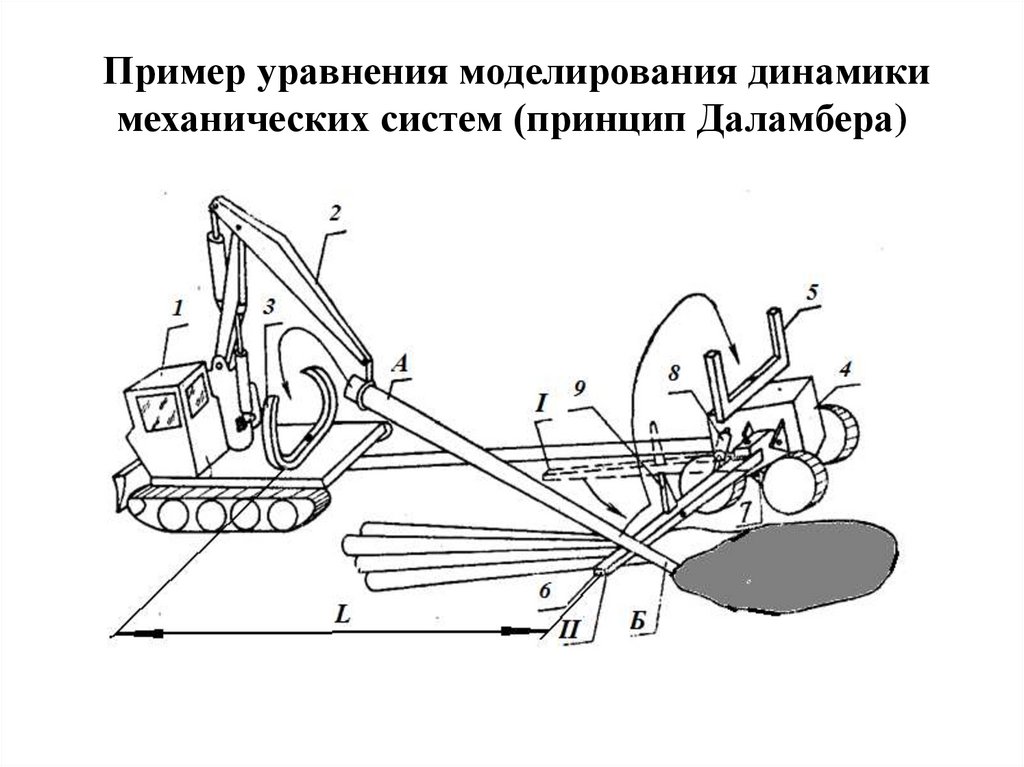
56.
Пример уравнения моделирования динамикимеханических систем (принцип Даламбера)
57.
ПОЛИГОННЫЕ ИСПЫТАНИЯ ПТМ58.
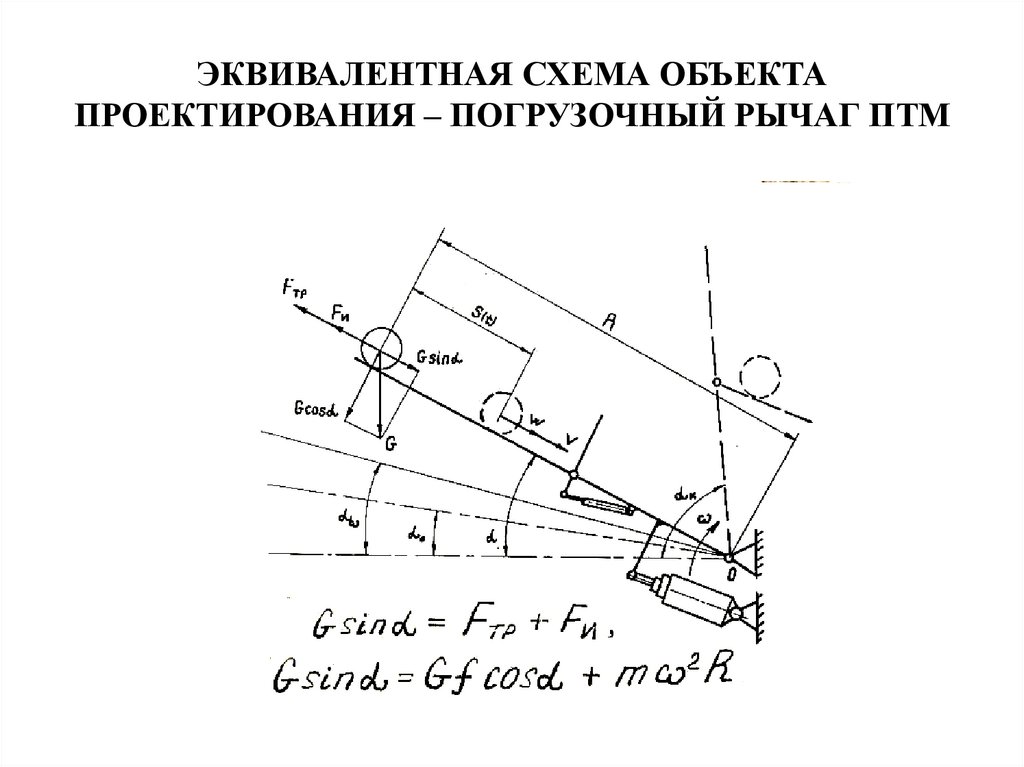
ЭКВИВАЛЕНТНАЯ СХЕМА ОБЪЕКТАПРОЕКТИРОВАНИЯ – ПОГРУЗОЧНЫЙ РЫЧАГ ПТМ
59.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА СКОЛЬЖЕНИЯСТВОЛА ПО РЫЧАГУ ПРИ ПОГРУЗКЕ
60.
Общее уравнение динамики, как основамоделирования динамических систем
61.
Уравнение Лагранжа второго рода62.
Пример уравнения Лагранжа второго родадля системы с двумя степенями свободы
63.
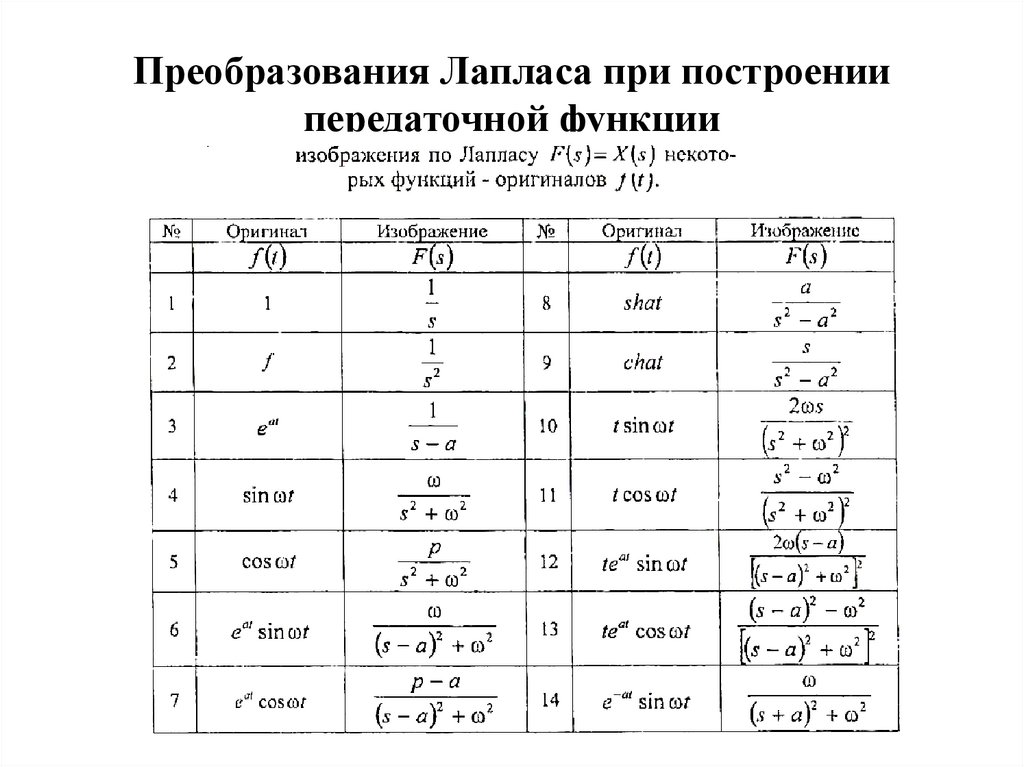
Преобразования Лапласа при построениипередаточной функции
64.
Преобразования Лапласа при построениипередаточной функции
65.
Преобразования Лапласа при построениипередаточной функции
66.
Частотная характеристика передаточной функциидетерминированной динамической системы
67.
Уравнение частотной характеристикидинамической системы
68.
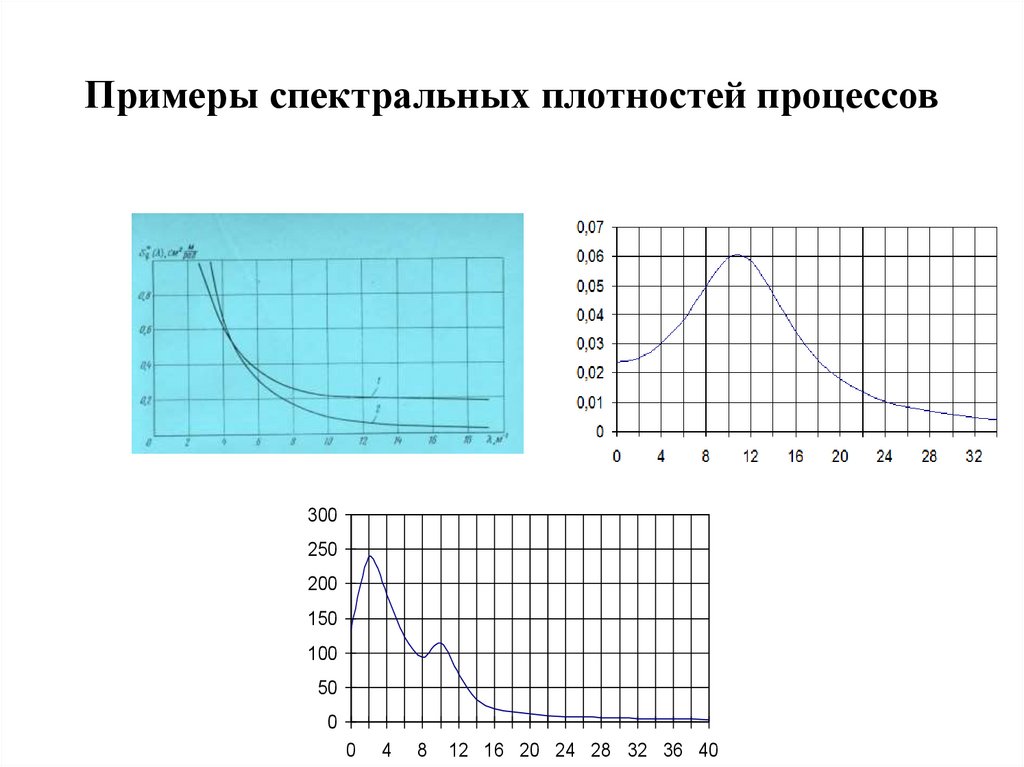
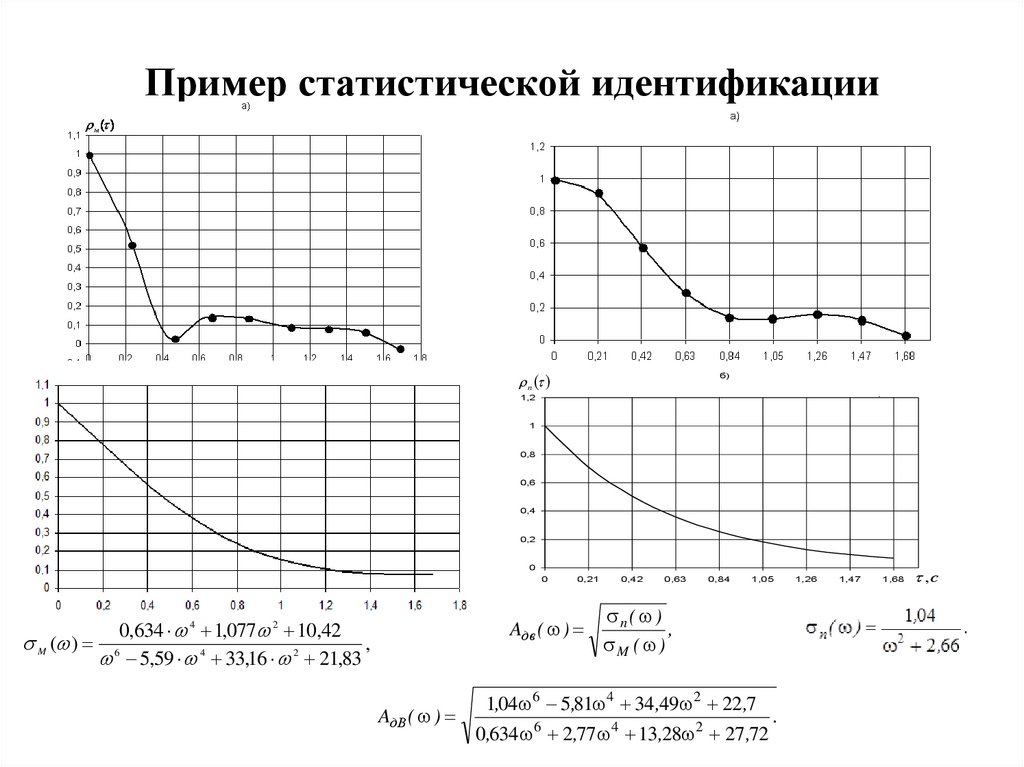
Моделирование модуля передаточной функциистатистической динамической системы (амплитудночастотной характеристики)
• Теорией случайных процессов
называется математическая наука, изучающая закономерности случайных
явлений в динамике их развития.
Случайные процессы являются удобной математической моделью
функций времени, значения которых случайные величины.
Запись случайного процесса будем называть реализацией случайного
процесса.
Совокупность всех реализаций случайного процесса называется
ансамблем реализаций.
Можно сказать, что случайный процесс – это однопараметрическое
семейство случайных величин, заданных на одном и том же
пространстве элементарных событий, зависящих от значений параметра
t.
• Часто случайный процесс f(ω, t) обозначается как f(t), где аргумент t
имеет смысл времени.
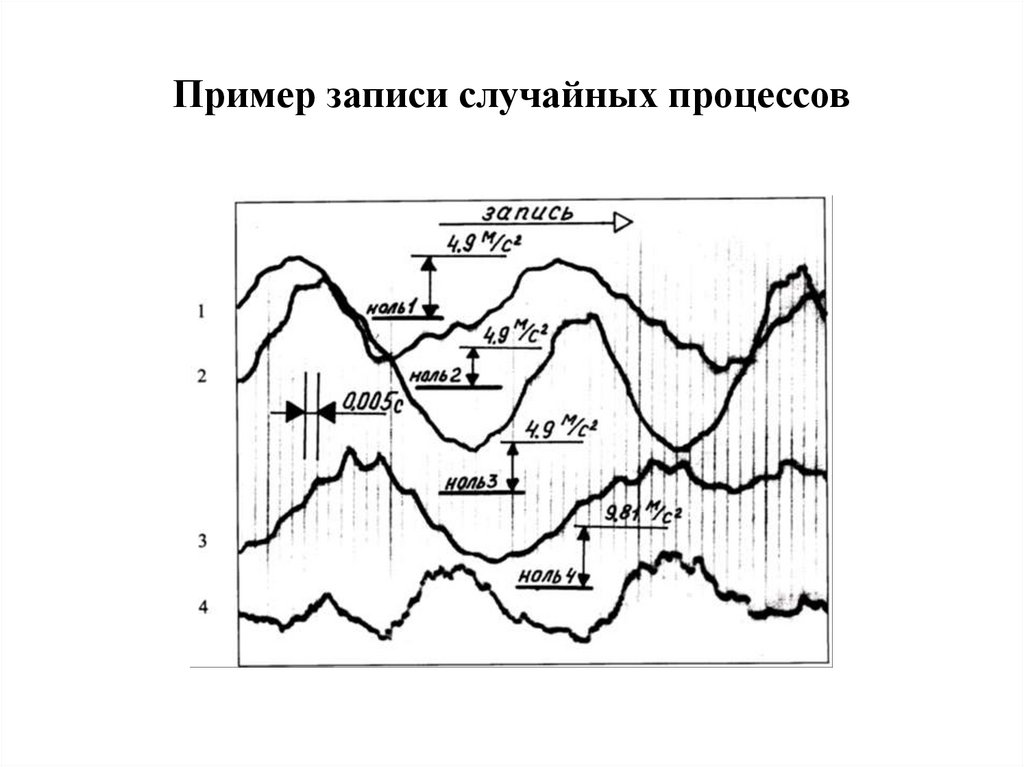
69.
Пример записи случайных процессов70.
Характеристики и свойства однородныхэргодичных случайных процессов
• Математическим ожиданием случайного процесса или его средним
значением называется неслучайная функция m х(t), t принадлежит
времени реализации T.
• Дисперсией случайного процесса D (t) называется неслучайная
неотрицательная функция D х(t) , которая при любом значении
аргумента t равна дисперсии соответствующего сечения случайного
процесса.
• Среднеквадратическим или стандартным отклонением
случайного процесса называют неслучайную функцию равную корню
квадратному из дисперсии.
• Центрированный случайный процесс – процесс равный разнице
между его текущим значением и мат. ожиданием процесса.
71.
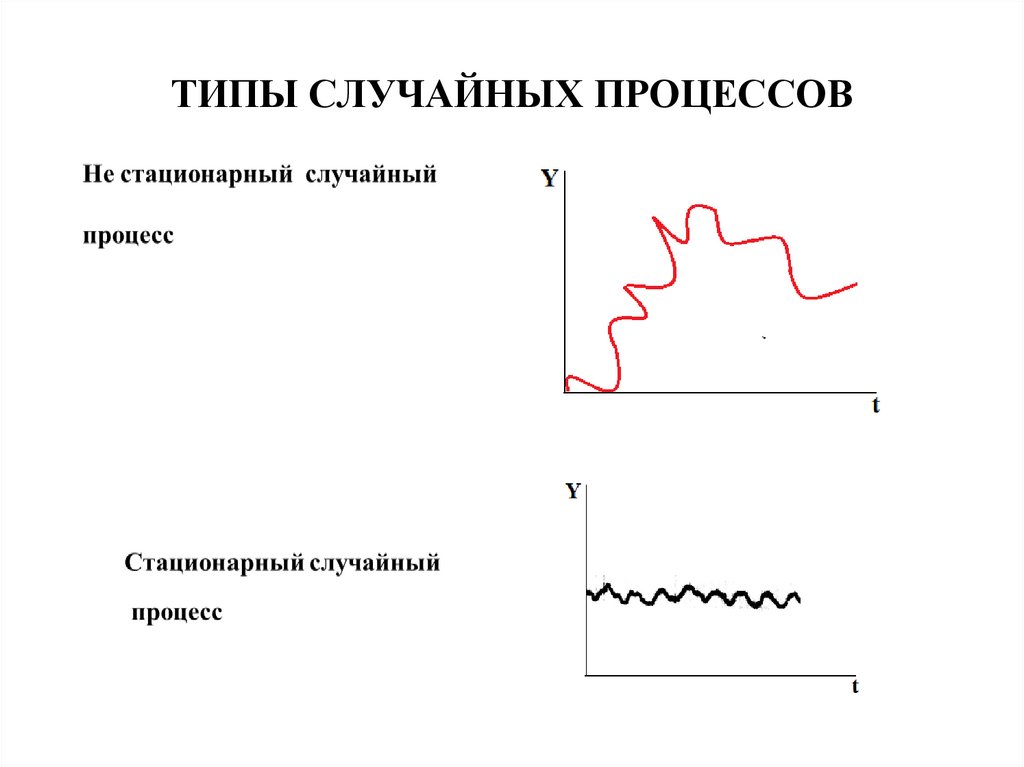
ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ72.
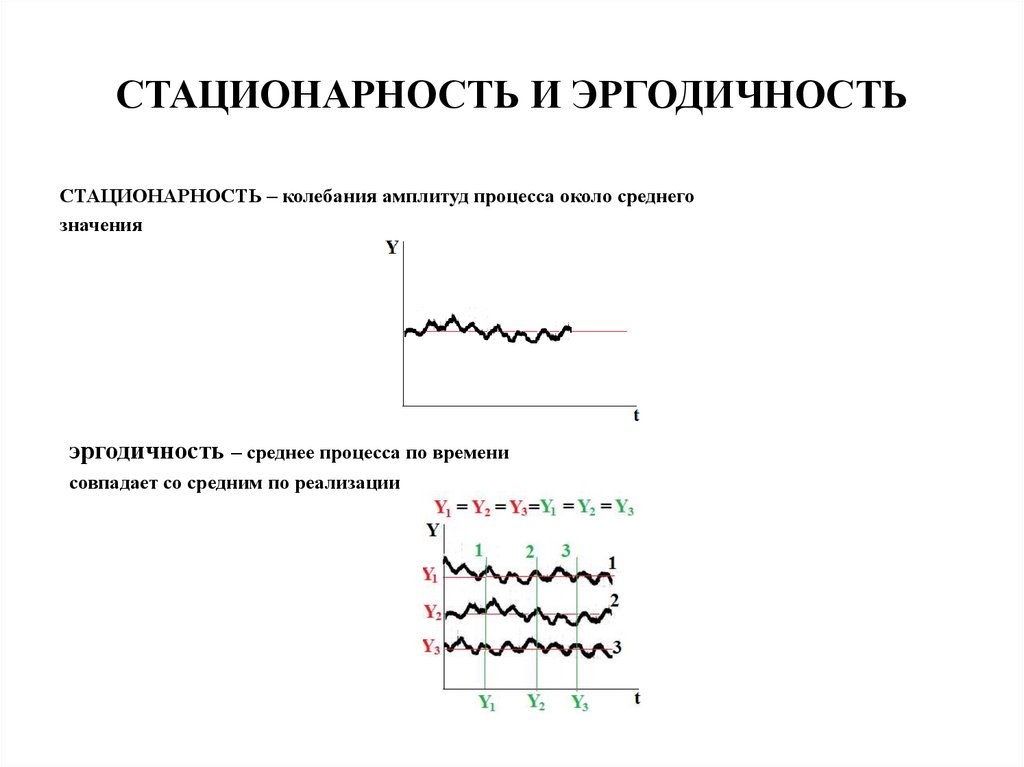
СТАЦИОНАРНОСТЬ И ЭРГОДИЧНОСТЬСТАЦИОНАРНОСТЬ – колебания амплитуд процесса около среднего
значения
эргодичность – среднее процесса по времени
совпадает со средним по реализации




































































 industry
industry








