Методы моделирования систем и процессов управления

1. МЕТОДЫ МОДЕЛИРОВАНИЯ СИСТЕМ И ПРОЦЕССОВ УПРАВЛЕНИЯ

Конспект лекций
в схемах

2.

Содержание занятия
1.
2.
3.
4.
5.
6.
7.
Понятие модели.
Назначение моделей.
Виды моделей.
Уровни моделирования.
Классификации методов моделирования систем.
Аналитические и статистические методы.
Математическая логика.

3. МОДЕЛЬ

Модель – (французское modele, от латинского modulus - мера, образец).
1. Устройство, воспроизводящее, имитирующее строение и действие какого-либо другого
(«моделируемого») устройства в научных, производственных (при испытаниях) или спортивных целях.
2. В широком смысле – любой образ, аналог (мысленный или условный: изображение, описание,
схема, чертеж, график, план, карта и т.п.) какого-либо объекта, процесса или явления («оригинала»
данной модели), используемый в качестве его «заместителя», «представителя».
3. В математике и логике моделью какой-либо системы аксиом называют любую совокупность
(абстрактных) объектов, свойства которых и отношения между которыми удовлетворяют данным
аксиомам, служащим тем самым совместным (неявным) определением такой совокупности.
4. Модель в языкознании - абстрактное понятие эталона или образца какой-либо системы
(фонологической, грамматической и т.п.), представление самых общих характеристик какого-либо
языкового явления; общая схема описания системы языка или какой-либо его подсистемы

4.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Модель
это объект любой природы, который, отображая или воспроизводя исследуемый
объект, способен замещать его так, что изучение замещающего объекта позволяет
получить новую информацию о замещаемом объекте.
Оригинал
Замещаемый при моделировании объект.
Моделирование
метод изучения сложного объекта путем его замены более удобным для
исследования объектом, сохраняющим существенные черты изучаемого объекта, а
также процесс построения замещающего объекта.
Подобие
сходство объектов одной физической природы.
Аналогия
сходство объектов различной физической природы.

5.

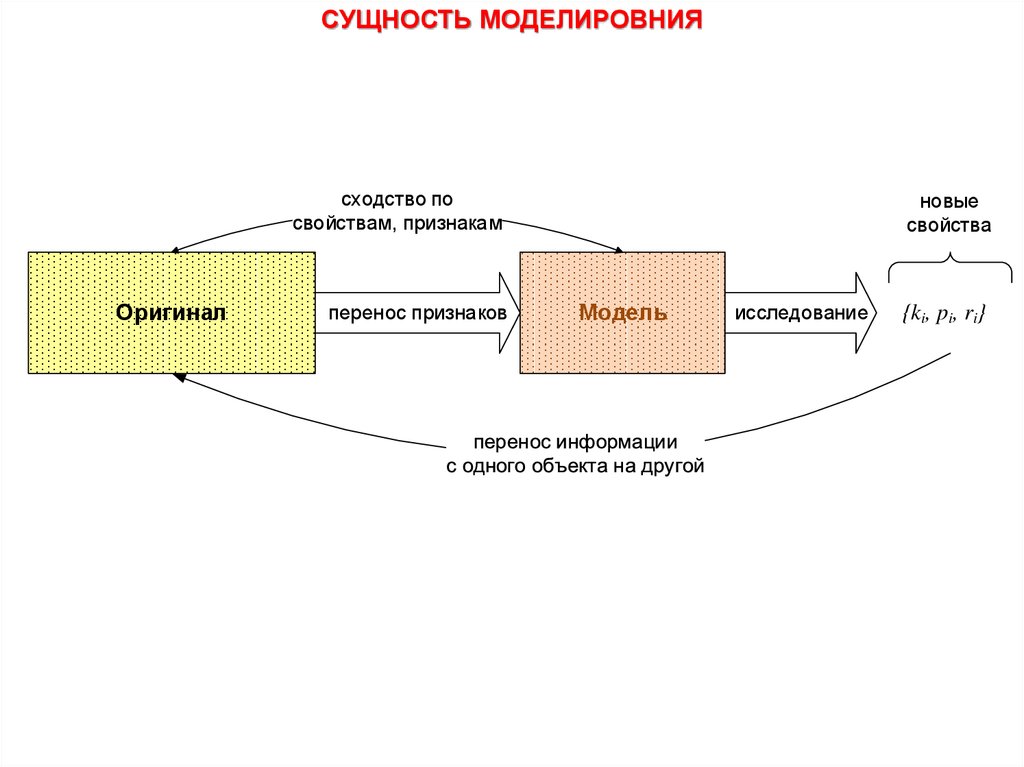
СУЩНОСТЬ МОДЕЛИРОВНИЯ
сходство по
свойствам, признакам
Оригинал
перенос признаков
новые
свойства
Модель
исследование
{ki, pi, ri}

6.

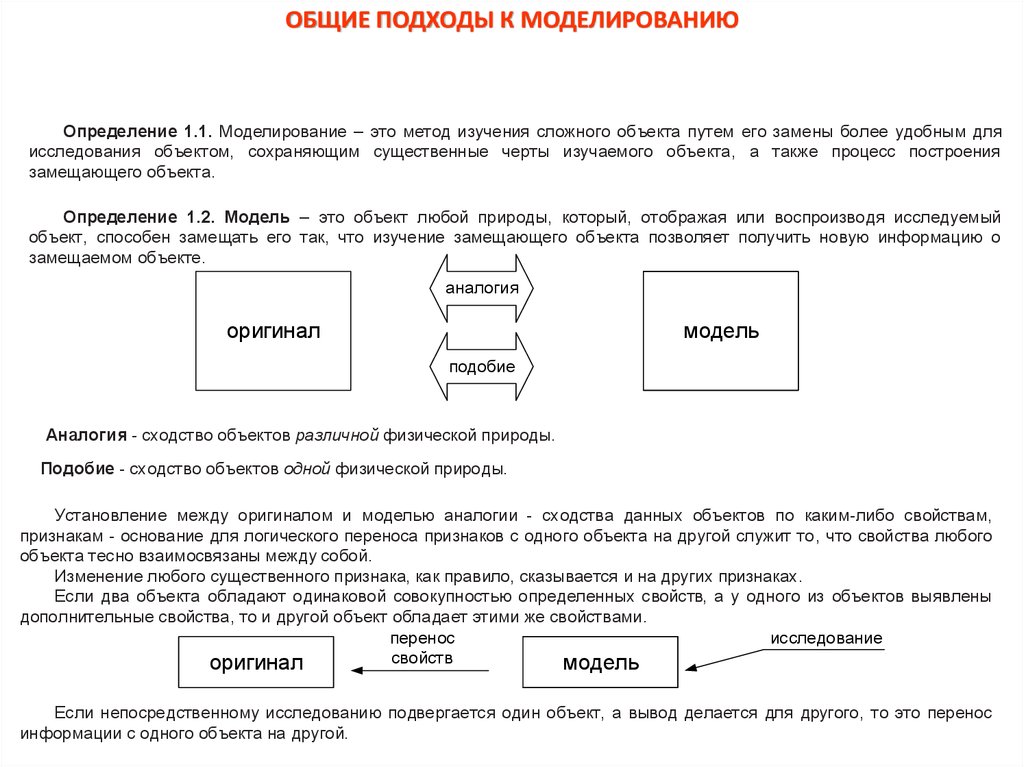
ОБЩИЕ ПОДХОДЫ К МОДЕЛИРОВАНИЮ
Определение 1.1. Моделирование – это метод изучения сложного объекта путем его замены более удобным для
исследования объектом, сохраняющим существенные черты изучаемого объекта, а также процесс построения
замещающего объекта.
Определение 1.2. Модель – это объект любой природы, который, отображая или воспроизводя исследуемый
объект, способен замещать его так, что изучение замещающего объекта позволяет получить новую информацию о
замещаемом объекте.
аналогия
оригинал
модель
подобие
Аналогия - сходство объектов различной физической природы.
Подобие - сходство объектов одной физической природы.
Установление между оригиналом и моделью аналогии - сходства данных объектов по каким-либо свойствам,
признакам - основание для логического переноса признаков с одного объекта на другой служит то, что свойства любого
объекта тесно взаимосвязаны между собой.
Изменение любого существенного признака, как правило, сказывается и на других признаках.
Если два объекта обладают одинаковой совокупностью определенных свойств, а у одного из объектов выявлены
дополнительные свойства, то и другой объект обладает этими же свойствами.
исследование
перенос
свойств
оригинал
модель
Если непосредственному исследованию подвергается один объект, а вывод делается для другого, то это перенос
информации с одного объекта на другой.

7.

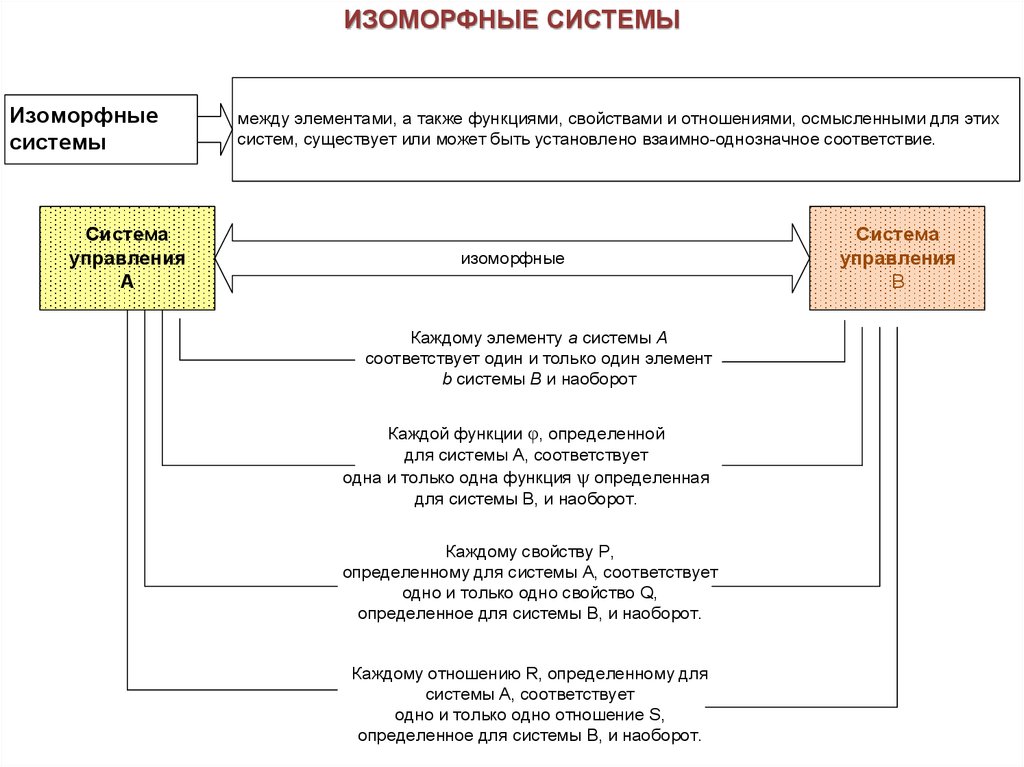
ИЗОМОРФНЫЕ СИСТЕМЫ
Изоморфные
системы
Система
управления
А
между элементами, а также функциями, свойствами и отношениями, осмысленными для этих
систем, существует или может быть установлено взаимно-однозначное соответствие.
изоморфные
Каждому элементу а системы A
соответствует один и только один элемент
b системы B и наоборот
Каждой функции φ, определенной
для системы А, соответствует
одна и только одна функция ѱ определенная
для системы B, и наоборот.
Каждому свойству P,
определенному для системы A, соответствует
одно и только одно свойство Q,
определенное для системы B, и наоборот.
Каждому отношению R, определенному для
системы A, соответствует
одно и только одно отношение S,
определенное для системы B, и наоборот.
Система
управления
В

8.

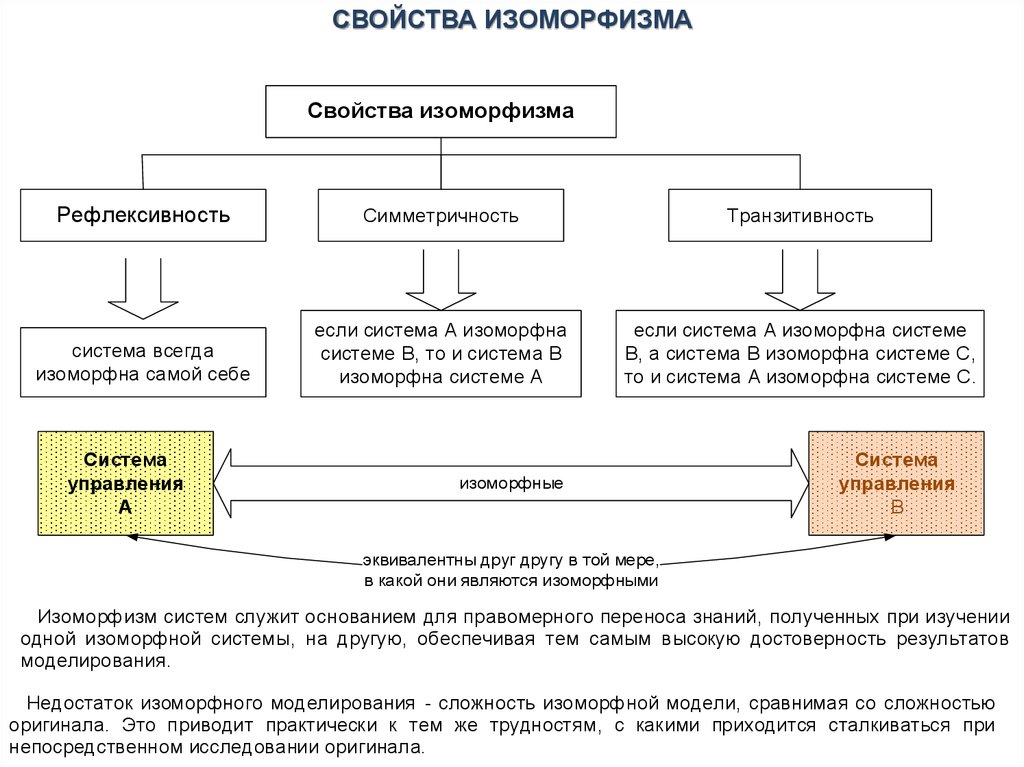
СВОЙСТВА ИЗОМОРФИЗМА
Свойства изоморфизма
Рефлексивность
Симметричность
Транзитивность
система всегда
изоморфна самой себе
если система А изоморфна
системе B, то и система B
изоморфна системе А
если система А изоморфна системе
B, а система B изоморфна системе С,
то и система А изоморфна системе С.
Система
управления
А
изоморфные
Система
управления
В
эквивалентны друг другу в той мере,
в какой они являются изоморфными
Изоморфизм систем служит основанием для правомерного переноса знаний, полученных при изучении
одной изоморфной системы, на другую, обеспечивая тем самым высокую достоверность результатов
моделирования.
Недостаток изоморфного моделирования - сложность изоморфной модели, сравнимая со сложностью
оригинала. Это приводит практически к тем же трудностям, с какими приходится сталкиваться при
непосредственном исследовании оригинала.

9.

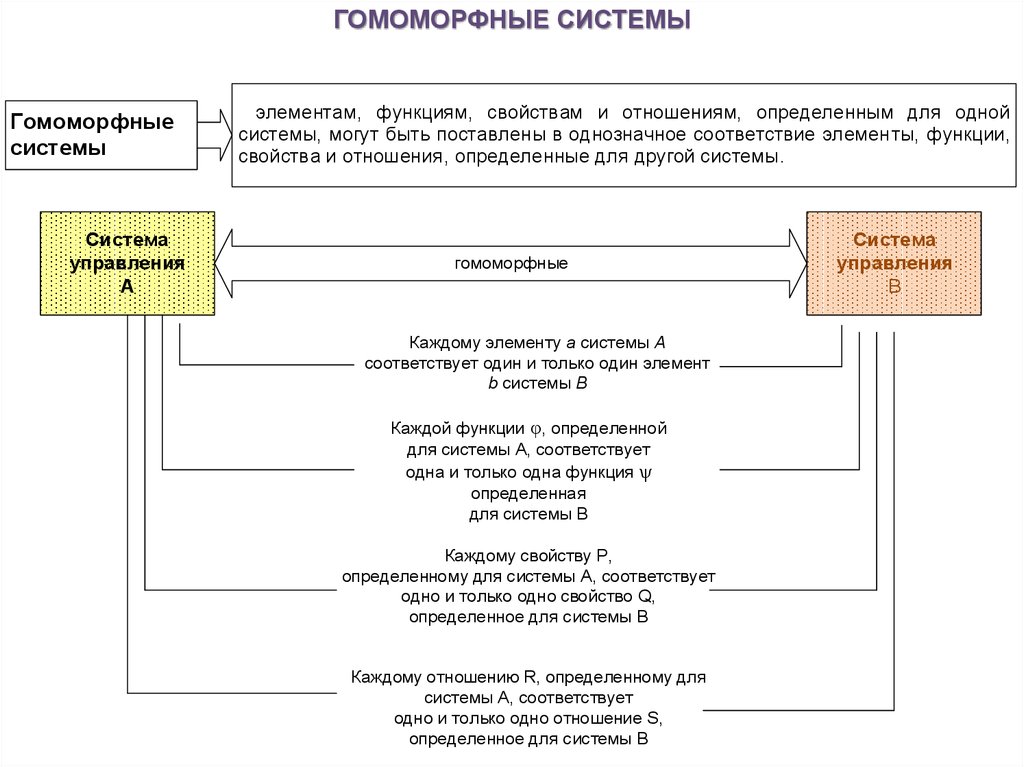
ГОМОМОРФНЫЕ СИСТЕМЫ
Гомоморфные
системы
Система
управления
А
элементам, функциям, свойствам и отношениям, определенным для одной
системы, могут быть поставлены в однозначное соответствие элементы, функции,
свойства и отношения, определенные для другой системы.
гомоморфные
Каждому элементу а системы A
соответствует один и только один элемент
b системы B
Каждой функции φ, определенной
для системы А, соответствует
одна и только одна функция ѱ
определенная
для системы B
Каждому свойству P,
определенному для системы A, соответствует
одно и только одно свойство Q,
определенное для системы B
Каждому отношению R, определенному для
системы A, соответствует
одно и только одно отношение S,
определенное для системы B
Система
управления
В

10.

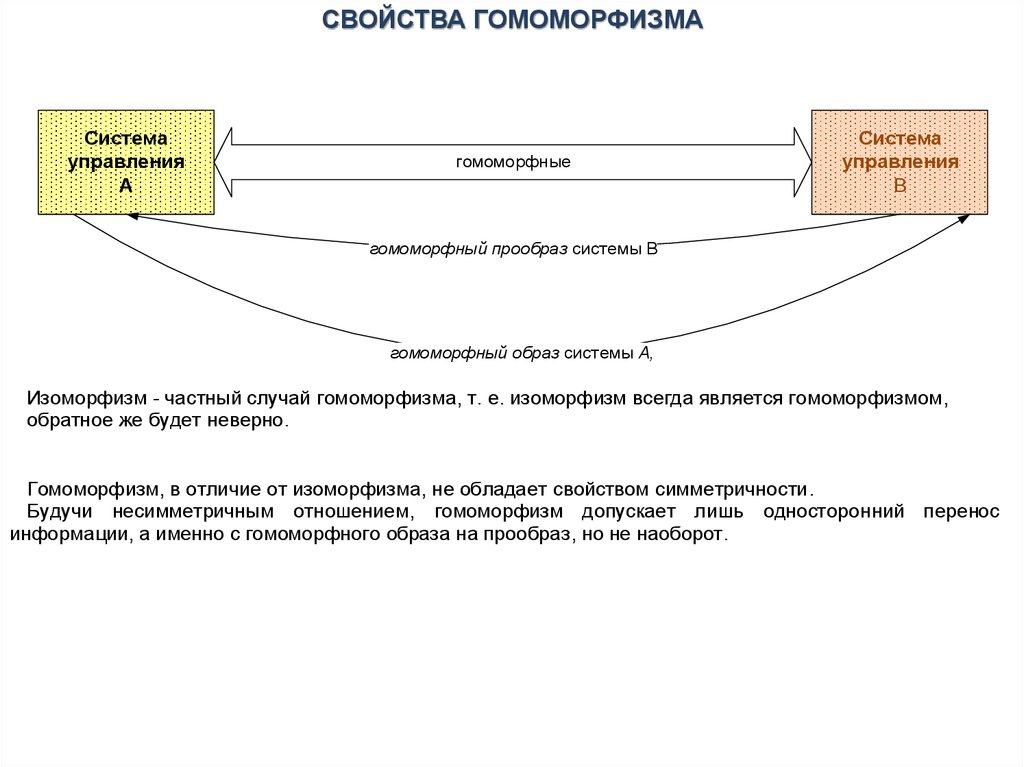
СВОЙСТВА ГОМОМОРФИЗМА
Система
управления
А
гомоморфные
Система
управления
В
гомоморфный прообраз системы B
гомоморфный образ системы А,
Изоморфизм - частный случай гомоморфизма, т. е. изоморфизм всегда является гомоморфизмом,
обратное же будет неверно.
Гомоморфизм, в отличие от изоморфизма, не обладает свойством симметричности.
Будучи несимметричным отношением, гомоморфизм допускает лишь односторонний перенос
информации, а именно с гомоморфного образа на прообраз, но не наоборот.

11.

ПОДХОДЫ ПРИ МОДЕЛИРОВАНИИ ГОМОМОРФНЫМИ МОДЕЛЯМИ
Подходы к гомоморфным моделям
Первый подход
Второй подход
Исключение из рассмотрения несущественных
элементов, функций, свойств и отношений
исследуемой системы (оригинала).
В результате получают более простую систему
(модель), пространство состояний которой имеет
размерность
меньшую,
чем
пространство
состояний исходной системы.
При этом каждому состоянию исходной
системы будет соответствовать только одно
состояние упрощенной системы, обратное будет
неверно.
Объединении некоторого множества состояний
исследуемой системы в одно, например, путем
перехода от рассмотрения всех состояний из
данного множества к рассмотрению только
принадлежности состояния к множеству.
В результате также получают более простую
систему с пространством состояний, меньшей
размерности, чем у исходной, и однозначным
соответствием состояний исходной системы
состояниям упрощенной.
Обратное соответствие будет неоднозначным.

12.

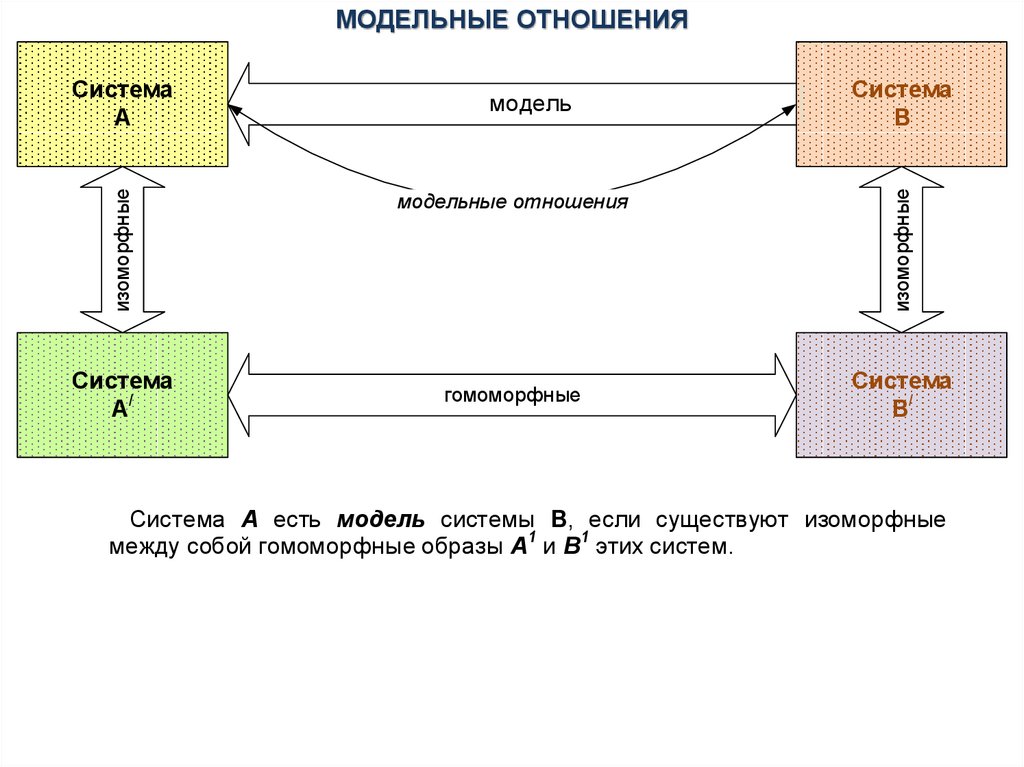
МОДЕЛЬНЫЕ ОТНОШЕНИЯ
Система
А/
модель
модельные отношения
гомоморфные
Система
В
изоморфные
изоморфные
Система
А
Система
В/
Система A есть модель системы B, если существуют изоморфные
между собой гомоморфные образы A1 и B1 этих систем.

13.

ОСНОВНЫЕ ЦЕЛИ И ПРИНЦИПЫ МОДЕЛИРОВАНИЯ
Основные цели моделирования
- описание строения и поведения системы;
- построение теорий и гипотез, объясняющих
наблюдаемое строение и поведение системы;
- прогнозирование
будущего
строения
и
поведения системы.
Основные принципы моделирования
- целенаправленность моделирования;
- "удобство"
модели
для
проведения
исследований;
- соответствие степени адекватности модели
целям моделирования.
Принцип целенаправленности моделирования означает, что модель
должна быть средством достижения целей, ради которых осуществляется моделирование.
Принцип "удобства" модели говорит о том, что проведение исследований на модели должно быть
проще и удобнее, чем на оригинале, а получаемые результаты исследований - допускать достаточно
простую интерпретацию.
Принцип соответствия степени адекватности модели целям моделирования предполагает, что
требуемая адекватность модели оригиналу определяется целями исследования. Если адекватность
модели будет ниже требуемой, то результаты моделирования будут недостаточно достоверными, чтобы
обеспечить достижение цели моделирования. Если же адекватность модели оригиналу будет выше
требуемой, то сложность модели может не обеспечить выполнения принципа "удобства" модели, т. е.
модель может оказаться сравнимой по сложности с оригиналом, либо результаты моделирования могут
не поддаваться интерпретации. В этом случае цели моделирования также не будут достигнуты.

14.

ТРЕБОВАНИЯ К МОДЕЛЯМ
Требования к моделям
- объективно соответствовать моделируемому объекту;
- позволять замещать изучаемый объект на определенных этапах исследования;
- давать в ходе исследования новую информацию, допускающую опытную проверку;
- содержать совокупность достаточно четких правил перехода от модельной информации
к информации о моделируемом объекте.
Модель должна быть:
- простой и понятной пользователю;
- целенаправленной;
- надежной в смысле гарантии от получения абсурдных результатов;
- удобной в обращении;
- полной с точки зрения достижения основных целей;
- адаптивной, т. е. допускающей изменение и развитие модели по мере получения
дополнительной информации;
- повторяемой.

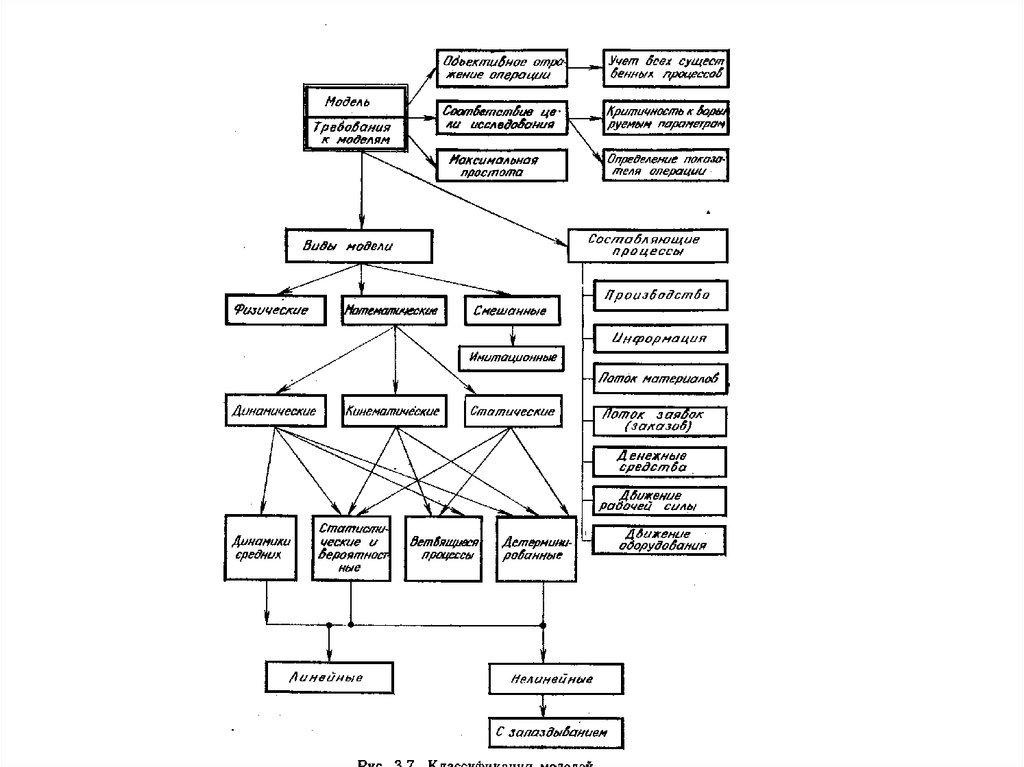
15.

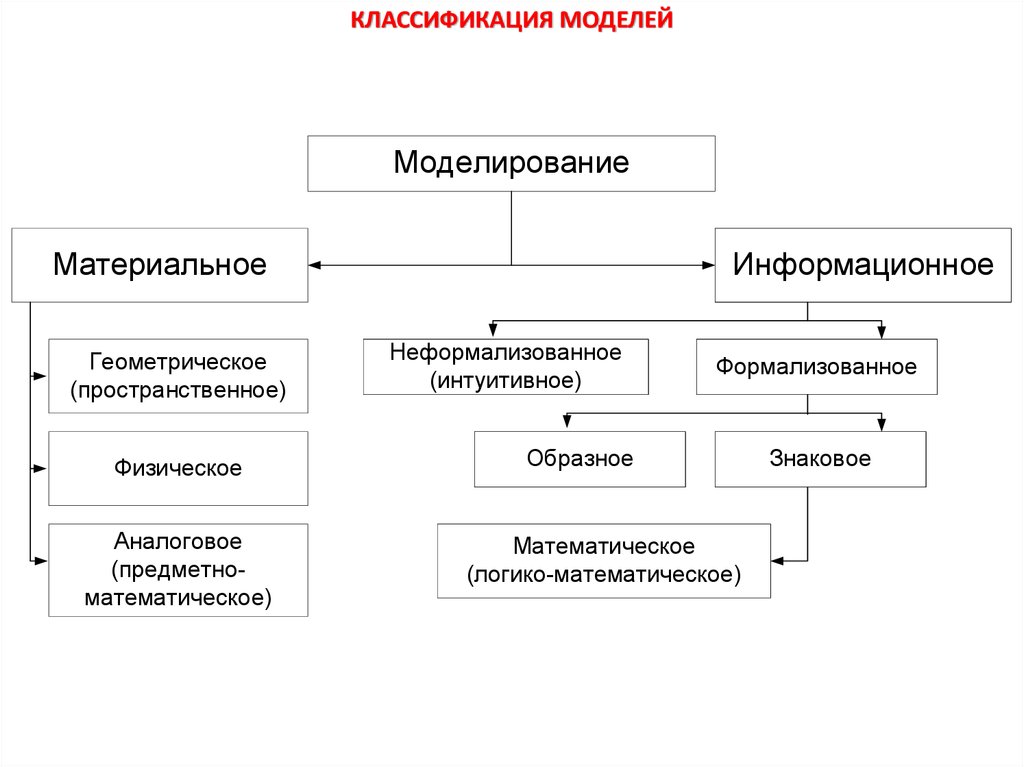
КЛАССИФИКАЦИЯ МОДЕЛЕЙ
Моделирование
Материальное
Геометрическое
(пространственное)
Физическое
Аналоговое
(предметноматематическое)
Информационное
Неформализованное
(интуитивное)
Формализованное
Образное
Математическое
(логико-математическое)
Знаковое

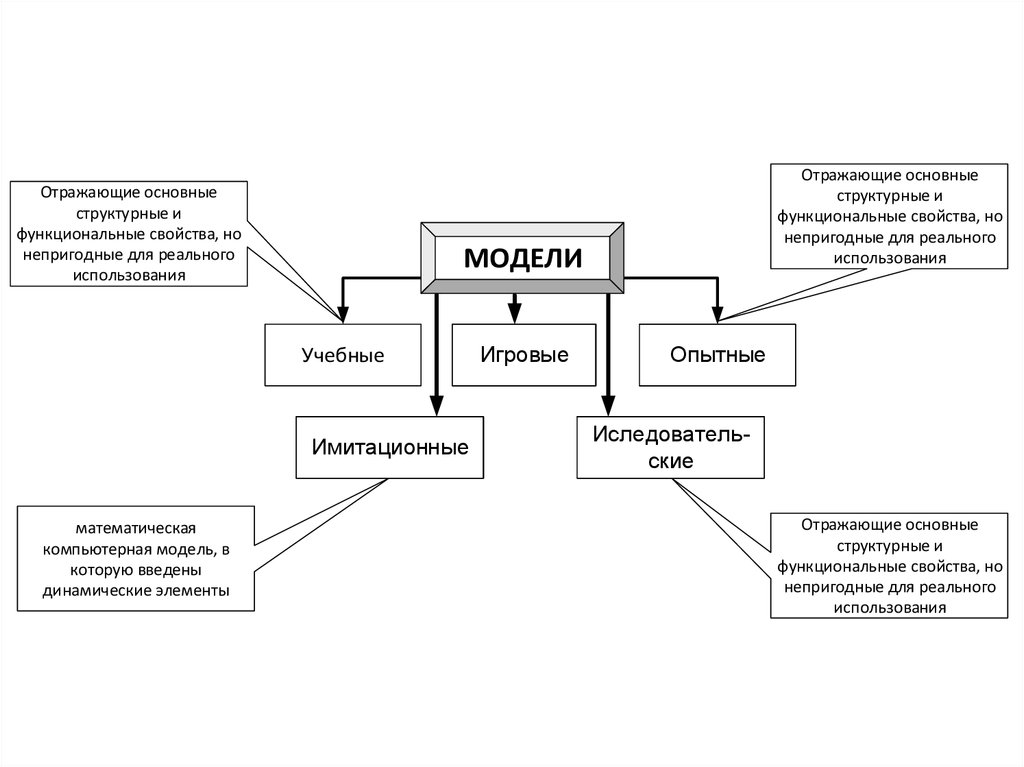
16.

Отражающие основные
структурные и
функциональные свойства, но
непригодные для реального
использования
МОДЕЛИ
Учебные
Имитационные
математическая
компьютерная модель, в
которую введены
динамические элементы
Отражающие основные
структурные и
функциональные свойства, но
непригодные для реального
использования
Игровые
Опытные
Иследовательские
Отражающие основные
структурные и
функциональные свойства, но
непригодные для реального
использования

17.

18.

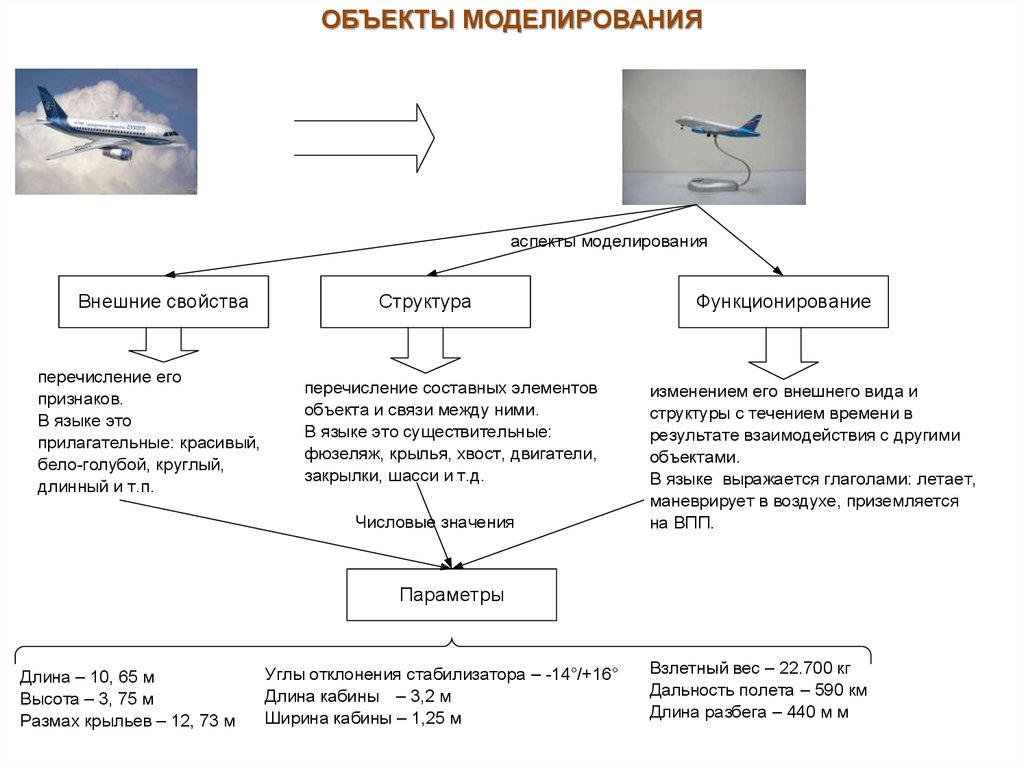
ОБЪЕКТЫ МОДЕЛИРОВАНИЯ
аспекты моделирования
Внешние свойства
перечисление его
признаков.
В языке это
прилагательные: красивый,
бело-голубой, круглый,
длинный и т.п.
Структура
перечисление составных элементов
объекта и связи между ними.
В языке это существительные:
фюзеляж, крылья, хвост, двигатели,
закрылки, шасси и т.д.
Числовые значения
Функционирование
изменением его внешнего вида и
структуры с течением времени в
результате взаимодействия с другими
объектами.
В языке выражается глаголами: летает,
маневрирует в воздухе, приземляется
на ВПП.
Параметры
Длина – 10, 65 м
Высота – 3, 75 м
Размах крыльев – 12, 73 м
Углы отклонения стабилизатора – -14°/+16°
Длина кабины – 3,2 м
Ширина кабины – 1,25 м
Взлетный вес – 22.700 кг
Дальность полета – 590 км
Длина разбега – 440 м м

19.

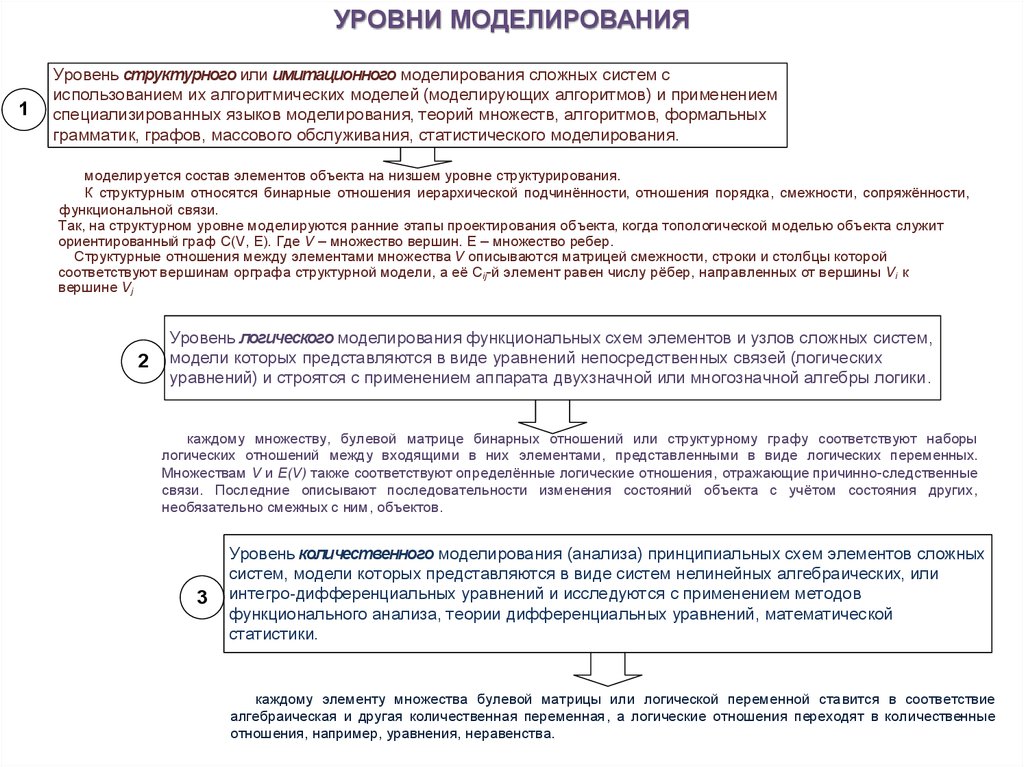
УРОВНИ МОДЕЛИРОВАНИЯ
1
Уровень структурного или имитационного моделирования сложных систем с
использованием их алгоритмических моделей (моделирующих алгоритмов) и применением
специализированных языков моделирования, теорий множеств, алгоритмов, формальных
грамматик, графов, массового обслуживания, статистического моделирования.
моделируется состав элементов объекта на низшем уровне структурирования.
К структурным относятся бинарные отношения иерархической подчинённости, отношения порядка, смежности, сопряжённости,
функциональной связи.
Так, на структурном уровне моделируются ранние этапы проектирования объекта, когда топологической моделью объекта служит
ориентированный граф C(V, E). Где V – множество вершин. E – множество ребер.
Структурные отношения между элементами множества V описываются матрицей смежности, строки и столбцы которой
соответствуют вершинам орграфа структурной модели, а её Cij-й элемент равен числу рёбер, направленных от вершины Vi к
вершине Vj
2
Уровень логического моделирования функциональных схем элементов и узлов сложных систем,
модели которых представляются в виде уравнений непосредственных связей (логических
уравнений) и строятся с применением аппарата двухзначной или многозначной алгебры логики.
каждому множеству, булевой матрице бинарных отношений или структурному графу соответствуют наборы
логических отношений между входящими в них элементами, представленными в виде логических переменных.
Множествам V и E(V) также соответствуют определённые логические отношения, отражающие причинно-следственные
связи. Последние описывают последовательности изменения состояний объекта с учётом состояния других ,
необязательно смежных с ним, объектов.
3
Уровень количественного моделирования (анализа) принципиальных схем элементов сложных
систем, модели которых представляются в виде систем нелинейных алгебраических, или
интегро-дифференциальных уравнений и исследуются с применением методов
функционального анализа, теории дифференциальных уравнений, математической
статистики.
каждому элементу множества булевой матрицы или логической переменной ставится в соответствие
алгебраическая и другая количественная переменная, а логические отношения переходят в количественные
отношения, например, уравнения, неравенства.

20.

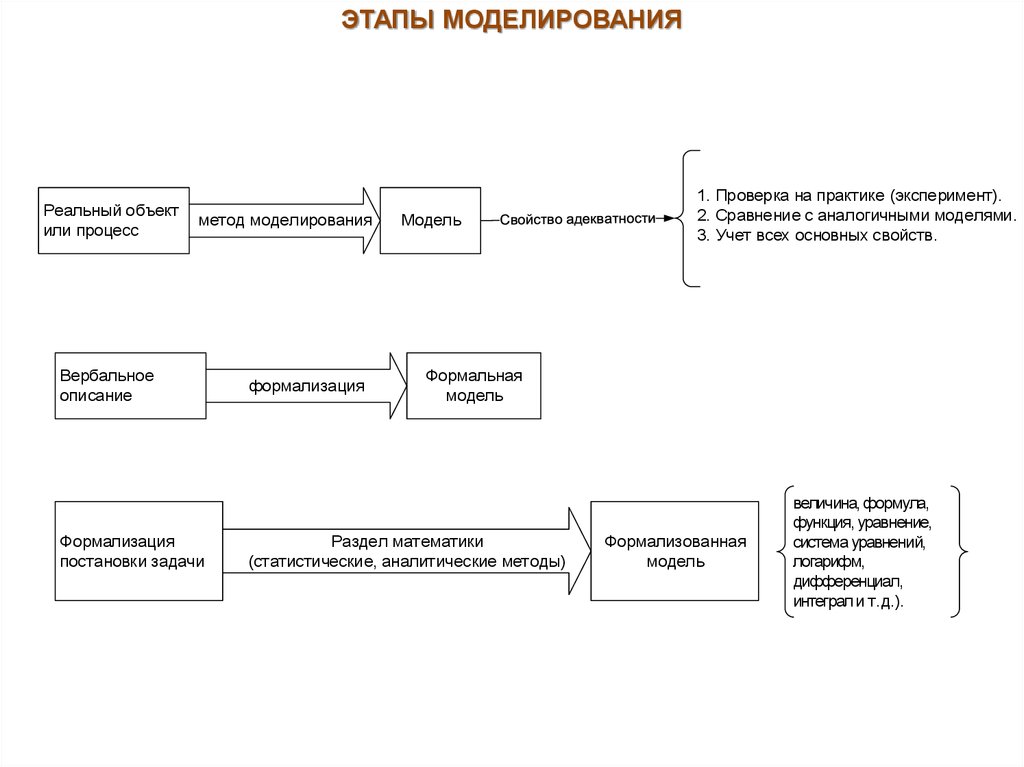
ЭТАПЫ МОДЕЛИРОВАНИЯ
Реальный объект
или процесс
метод моделирования
Вербальное
описание
Формализация
постановки задачи
формализация
Модель
1. Проверка на практике (эксперимент).
2. Сравнение с аналогичными моделями.
3. Учет всех основных свойств.
Формальная
модель
Раздел математики
(статистические, аналитические методы)
Формализованная
модель
величина, формула,
функция, уравнение,
система уравнений,
логарифм,
дифференциал,
интеграл и т.д.).

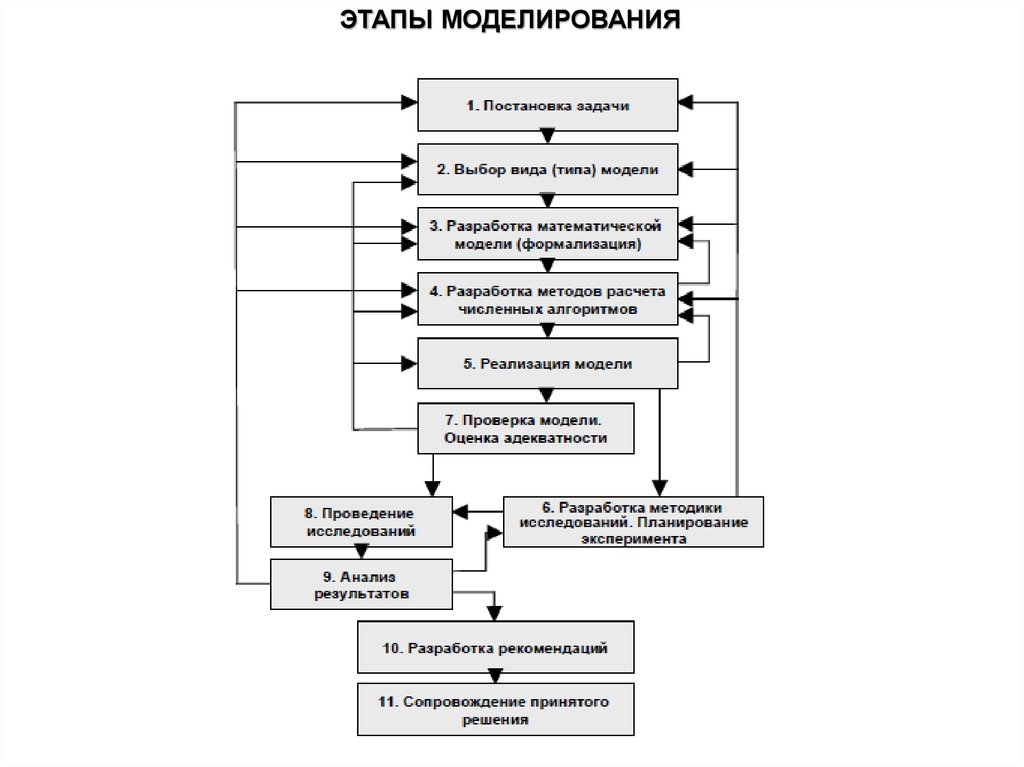
21.

ЭТАПЫ МОДЕЛИРОВАНИЯ

22.

Вербальное описание
Мозговая
атака
Сценарий
Формальное описание
Экспертные
оценки
Дерево
целей
Математиче Теория Статистичес Аналитическ
ская логика множеств кие методы ие методы
Методы моделирования
систем
Методы, направленные на
активизацию интуиции и опыта
специалистов (МАИС)
Методы организации
сложных экспертиз
Экспертные оценки
Морфологические
методы
Методы структуризации
(типа «дерева целей»,
сети и др.
Методы типа «Дельфи»
Методы типа сценариев
Методы типа «мозговой
атаки» или коллективной
генерации идей (КГИ)
Специальные методы
моделирования систем.
Методики постепенной
формализации целей
Имитационное
динамическое
моделирование
Структурнолингвистическое
моделирование
Ситуационное
моделирование
Методы
формализованного
представления
структур (МФПС)
Графические
Семиотические
Лингвистические
(математическая
лингвистика)
Логические
(математическая
логика)
Комплекси
рованные
методы
Графосемиотическое
моделирование
Топология
Теоретикомножественные
Статистические
Аналитические
Комбинаторика

23.

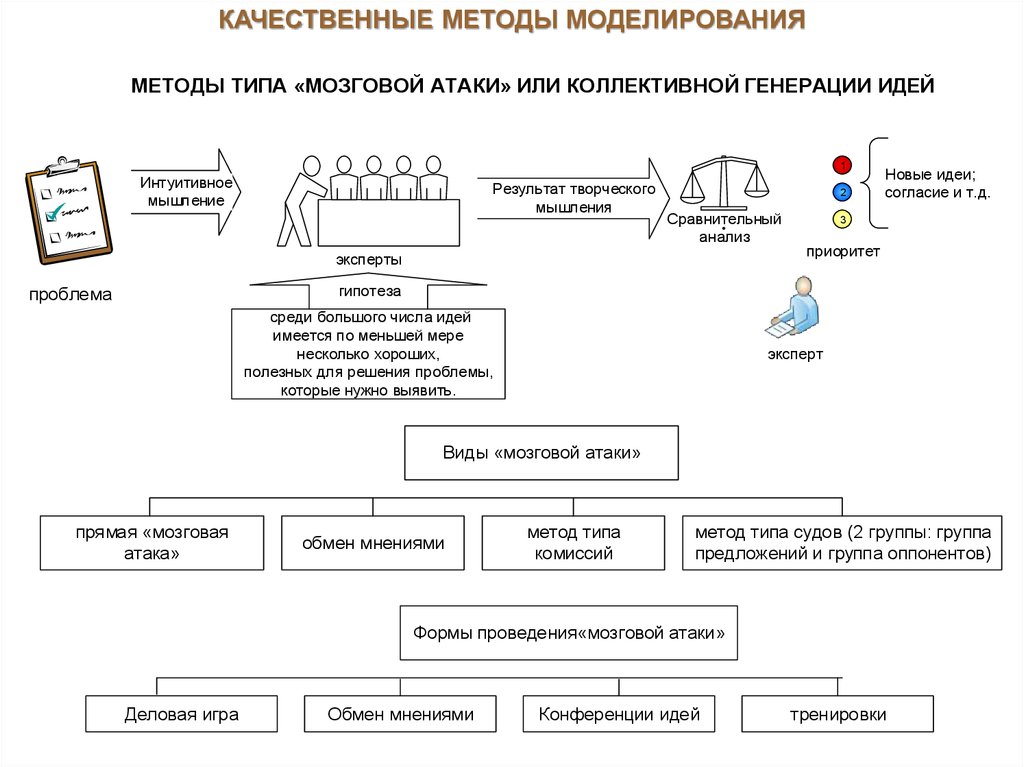
КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
МЕТОДЫ ТИПА «МОЗГОВОЙ АТАКИ» ИЛИ КОЛЛЕКТИВНОЙ ГЕНЕРАЦИИ ИДЕЙ
1
Интуитивное
мышление
Результат творческого
мышления
2
Сравнительный
анализ
эксперты
Новые идеи;
согласие и т.д.
3
приоритет
гипотеза
проблема
среди большого числа идей
имеется по меньшей мере
несколько хороших,
полезных для решения проблемы,
которые нужно выявить.
эксперт
Виды «мозговой атаки»
прямая «мозговая
атака»
обмен мнениями
метод типа
комиссий
метод типа судов (2 группы: группа
предложений и группа оппонентов)
Формы проведения«мозговой атаки»
Деловая игра
Обмен мнениями
Конференции идей
тренировки

24.

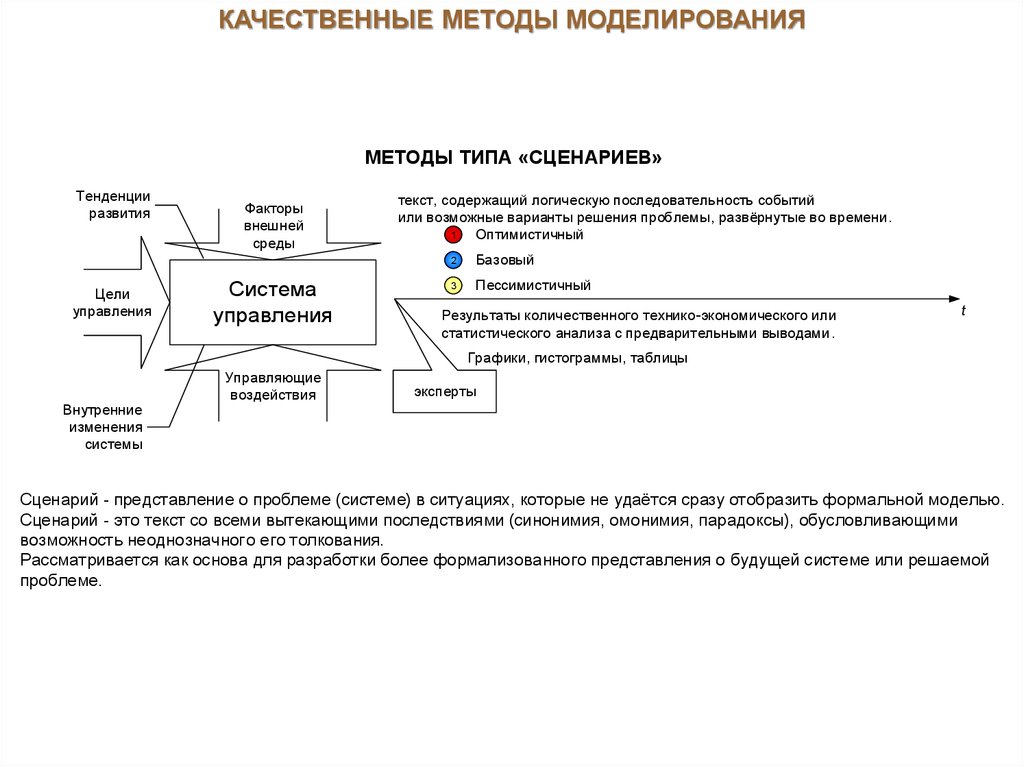
КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
МЕТОДЫ ТИПА «СЦЕНАРИЕВ»
Тенденции
развития
Цели
управления
Факторы
внешней
среды
Система
управления
текст, содержащий логическую последовательность событий
или возможные варианты решения проблемы, развёрнутые во времени.
1
Оптимистичный
2
Базовый
3
Пессимистичный
Результаты количественного технико-экономического или
статистического анализа с предварительными выводами.
t
Графики, гистограммы, таблицы
Внутренние
изменения
системы
Управляющие
воздействия
эксперты
Сценарий - представление о проблеме (системе) в ситуациях, которые не удаётся сразу отобразить формальной моделью.
Сценарий - это текст со всеми вытекающими последствиями (синонимия, омонимия, парадоксы), обусловливающими
возможность неоднозначного его толкования.
Рассматривается как основа для разработки более формализованного представления о будущей системе или решаемой
проблеме.

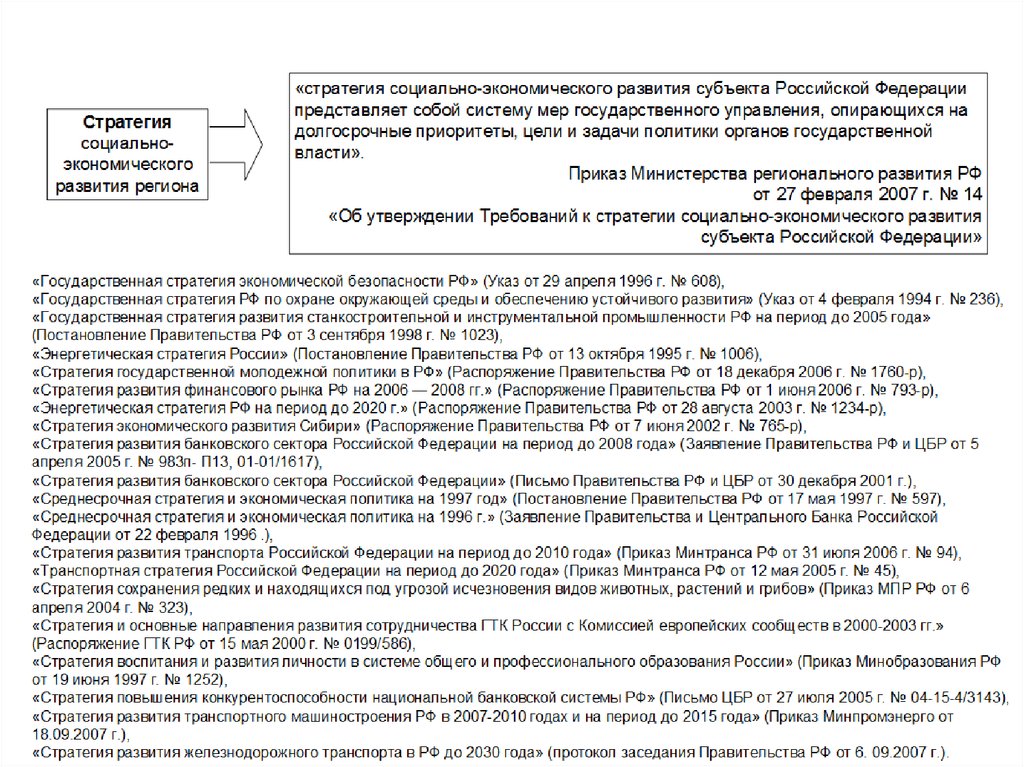
25.

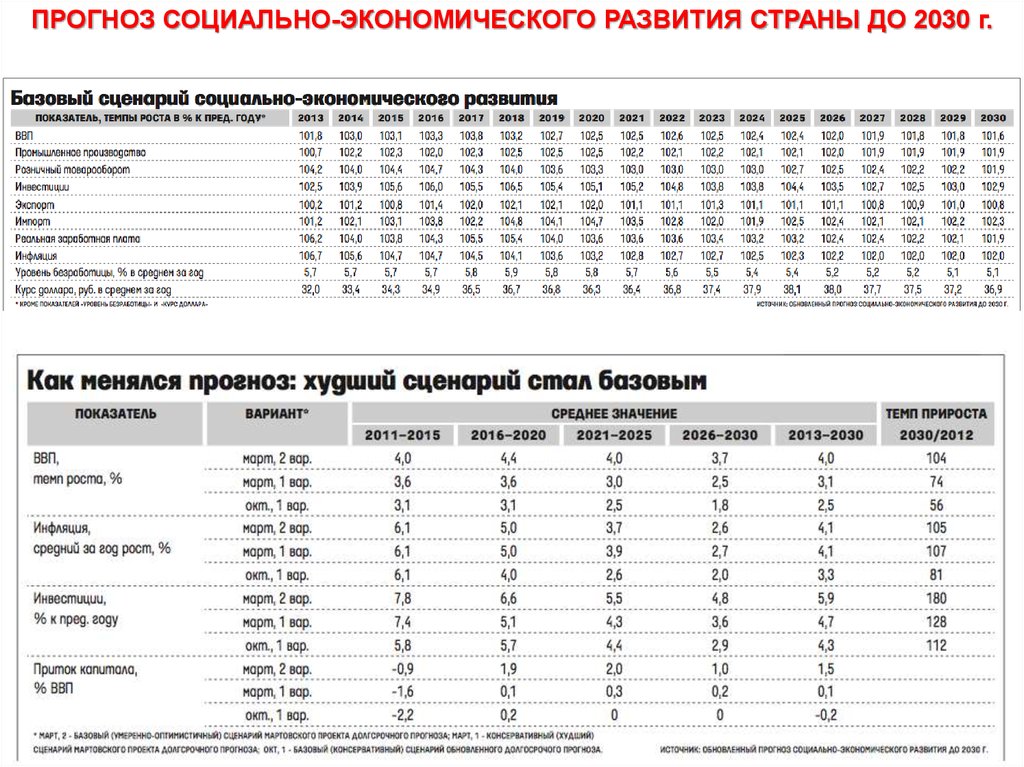
ПРОГНОЗ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ СТРАНЫ ДО 2030 г.

26.

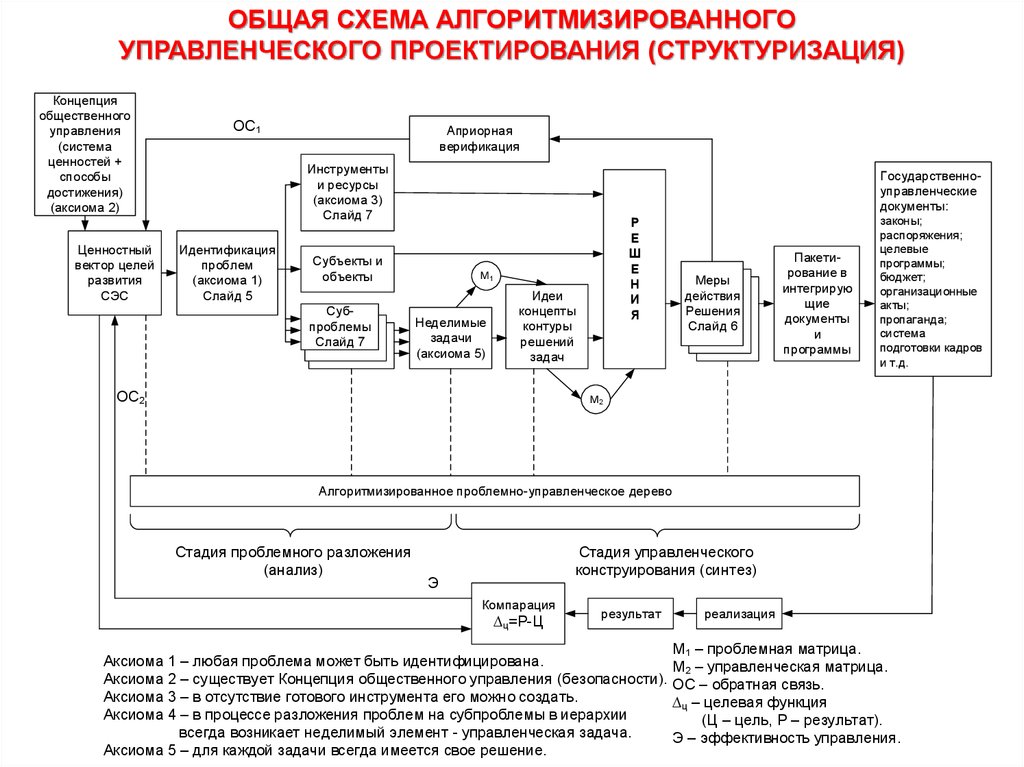
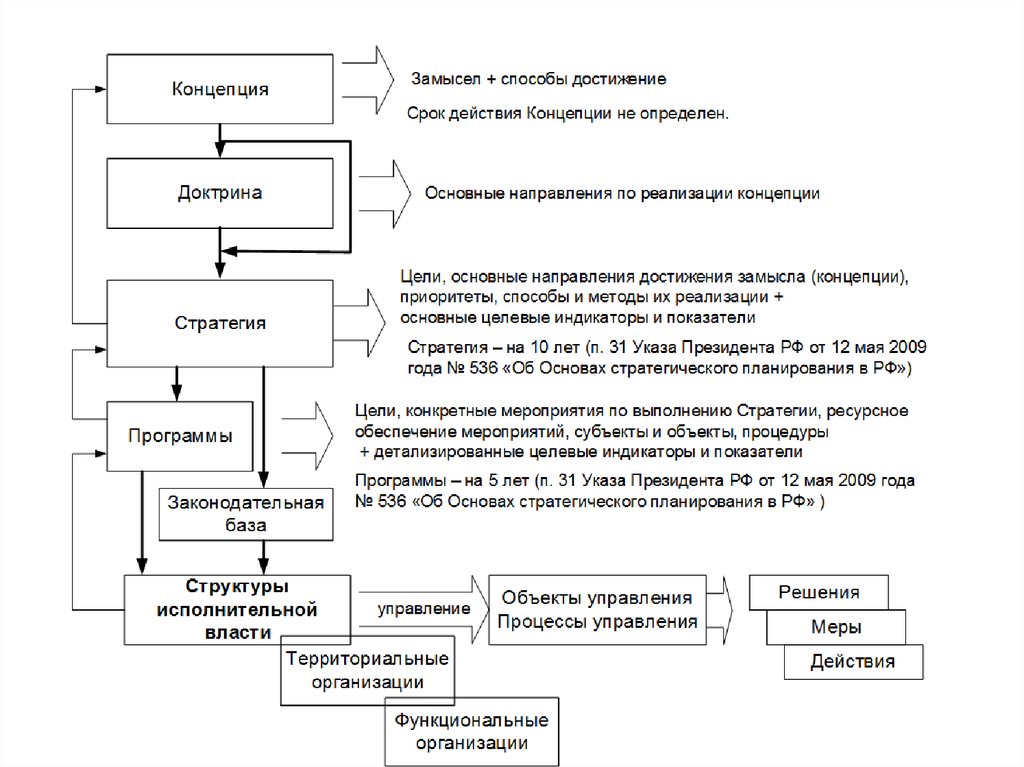
ОБЩАЯ СХЕМА АЛГОРИТМИЗИРОВАННОГО
УПРАВЛЕНЧЕСКОГО ПРОЕКТИРОВАНИЯ (СТРУКТУРИЗАЦИЯ)
Концепция
общественного
управления
(система
ценностей +
способы
достижения)
(аксиома 2)
Ценностный
вектор целей
развития
СЭС
ОС1
Априорная
верификация
Инструменты
и ресурсы
(аксиома 3)
Слайд 7
Идентификация
проблем
(аксиома 1)
Слайд 5
Государственноуправленческие
документы:
Субъекты и
объекты
Субпроблемы
Слайд 7
Р
Е
Ш
Е
Н
И
Я
М1
Неделимые
задачи
(аксиома 5)
Идеи
концепты
контуры
решений
задач
ОС2
Меры
действия
Решения
Слайд 6
Пакетирование в
интегрирую
щие
документы
и
программы
законы;
распоряжения;
целевые
программы;
бюджет;
организационные
акты;
пропаганда;
система
подготовки кадров
и т.д.
М2
Алгоритмизированное проблемно-управленческое дерево
Стадия проблемного разложения
(анализ)
Стадия управленческого
конструирования (синтез)
Э
Компарация
ц=Р-Ц
результат
реализация
М1 – проблемная матрица.
Аксиома 1 – любая проблема может быть идентифицирована.
М2 – управленческая матрица.
Аксиома 2 – существует Концепция общественного управления (безопасности). ОС – обратная связь.
Аксиома 3 – в отсутствие готового инструмента его можно создать.
ц – целевая функция
Аксиома 4 – в процессе разложения проблем на субпроблемы в иерархии
(Ц – цель, Р – результат).
всегда возникает неделимый элемент - управленческая задача.
Э – эффективность управления.
Аксиома 5 – для каждой задачи всегда имеется свое решение.

27.

ПРОБЛЕМНО-УПРАВЛЕНЧЕСКОЕ ДЕРЕВО
Ценностный вектор целей
развития СЭС (СПб)
Проблемы
I
II
N
...
А
Н
А
Л
И
З
Cубпроблемы
1-го уровня
2-го уровня
n-го уровня
неделимые
задачи
решения
...
...
...
...
Пакеты
решений
Программа
действий
t
С
И
Н
Т
Е
З

28.

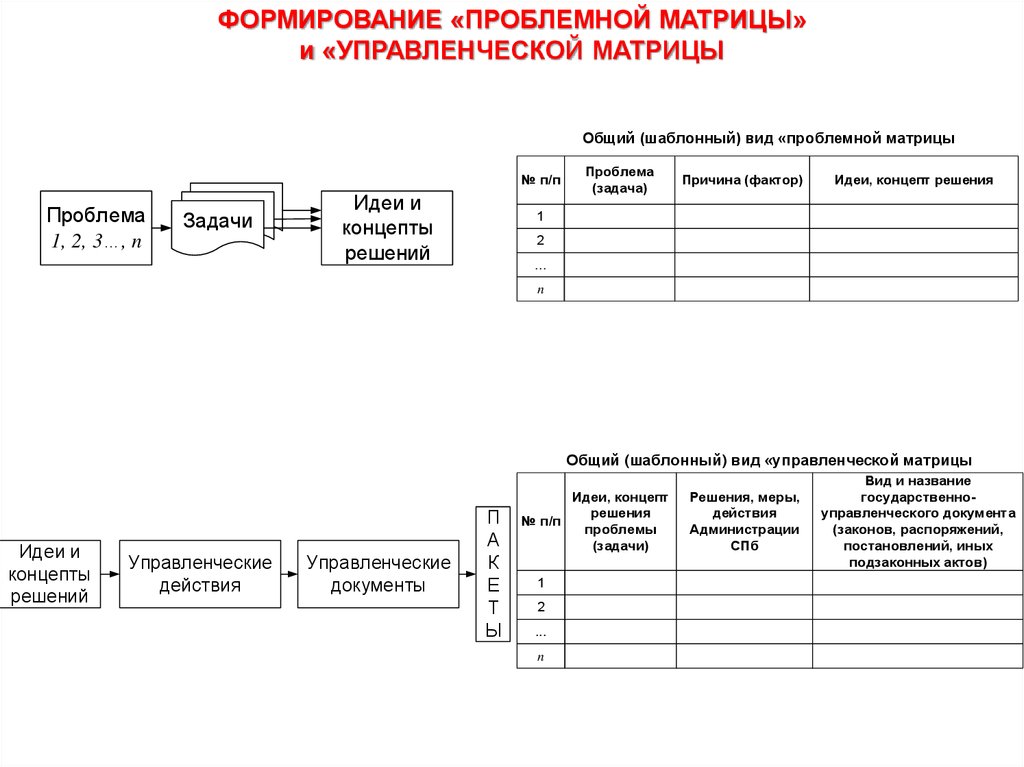
ФОРМИРОВАНИЕ «ПРОБЛЕМНОЙ МАТРИЦЫ»
и «УПРАВЛЕНЧЕСКОЙ МАТРИЦЫ
Общий (шаблонный) вид «проблемной матрицы
п/п
Проблема
1, 2, 3 , n
Задачи
Идеи и
концепты
решений
Проблема
(задача)
Причина (фактор)
Идеи, концепт решения
1
2
...
n
Общий (шаблонный) вид «управленческой матрицы
Идеи и
концепты
решений
Управленческие
действия
Управленческие
документы
П
А
К
Е
Т
Ы
Идеи, концепт
решения
п/п
проблемы
(задачи)
1
2
...
n
Решения, меры,
действия
Администрации
СПб
Вид и название
государственноуправленческого документа
(законов, распоряжений,
постановлений, иных
подзаконных актов)

29.

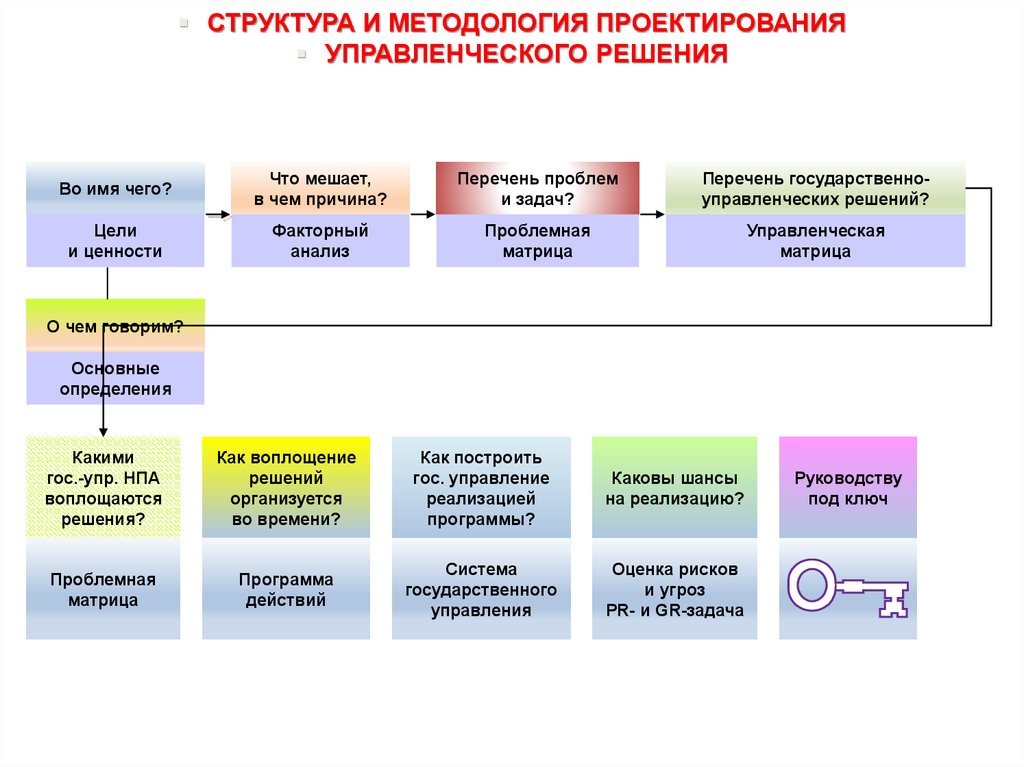
СТРУКТУРА И МЕТОДОЛОГИЯ ПРОЕКТИРОВАНИЯ
УПРАВЛЕНЧЕСКОГО РЕШЕНИЯ
Во имя чего?
Что мешает,
в чем причина?
Перечень проблем
и задач?
Перечень государственноуправленческих решений?
Цели
и ценности
Факторный
анализ
Проблемная
матрица
Управленческая
матрица
О чем говорим?
Основные
определения
Какими
гос.-упр. НПА
воплощаются
решения?
Как воплощение
решений
организуется
во времени?
Как построить
гос. управление
реализацией
программы?
Каковы шансы
на реализацию?
Проблемная
матрица
Программа
действий
Система
государственного
управления
Оценка рисков
и угроз
PR- и GR-задача
Руководству
под ключ

30.

31.

32.

33.

КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
МЕТОДЫ ЭКСПЕРТНЫХ ОЦЕНОК
формирования экспертных групп, включая:
- требования к экспертам;
- размеры группы;
- вопросы тренировки экспертов;
- оценки их компетентности.
1
2
3
4
5
формы экспертного опроса:
- разного рода анкетирования;
- интервью;
- смешанные формы опроса и методики организации опроса:
- методики анкетирования,
- мозговая атака,
- деловые игры и т.п.
подходы к оцениванию:
- ранжирование;
- нормирование;
- различные виды упорядочения, в том числе методы предпочтений, попарных сравнений
и др.);
методы обработки экспертных оценок;
- способы определения согласованности мнений экспертов, достоверности экспертных оценок:
- статистические методы оценки дисперсии,
- оценки вероятности для заданного диапазона изменений оценок,
- оценки ранговой корреляции Кендалла, Спирмена, коэффициента конкордации
- методы повышения согласованности оценок путём соответствующих способов обработки результатов
экспертного опроса.

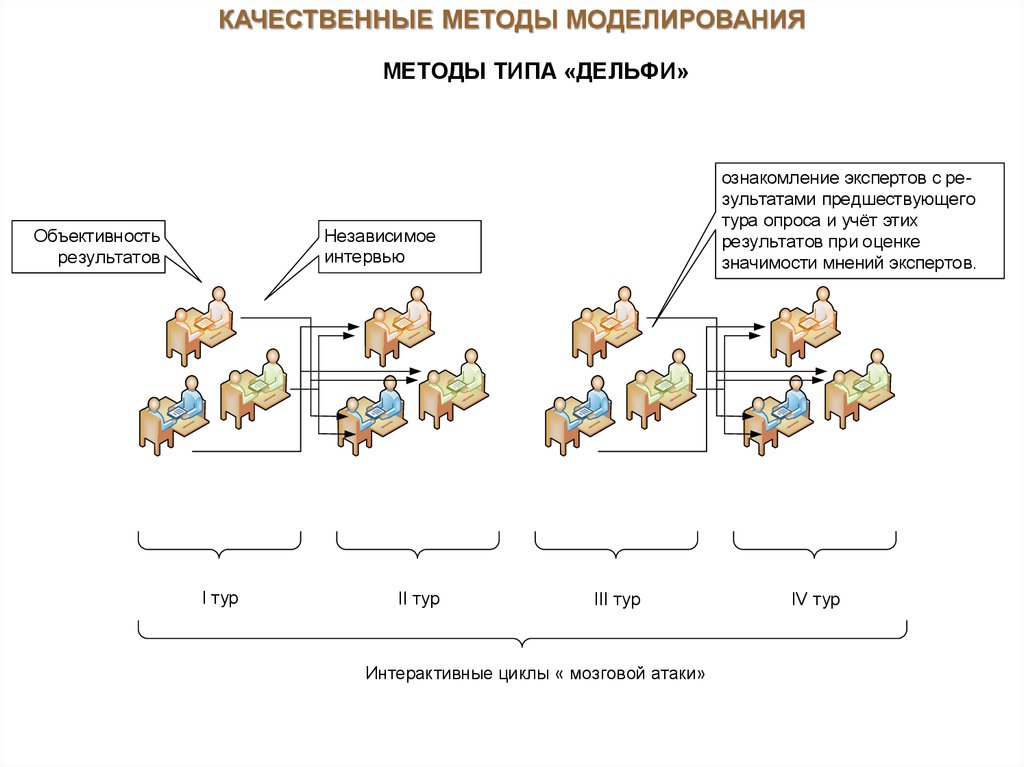
34.

КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
МЕТОДЫ ТИПА «ДЕЛЬФИ»
ознакомление экспертов с результатами предшествующего
тура опроса и учёт этих
результатов при оценке
значимости мнений экспертов.
Независимое
интервью
Объективность
результатов
I тур
II тур
III тур
Интерактивные циклы « мозговой атаки»
IV тур

35.

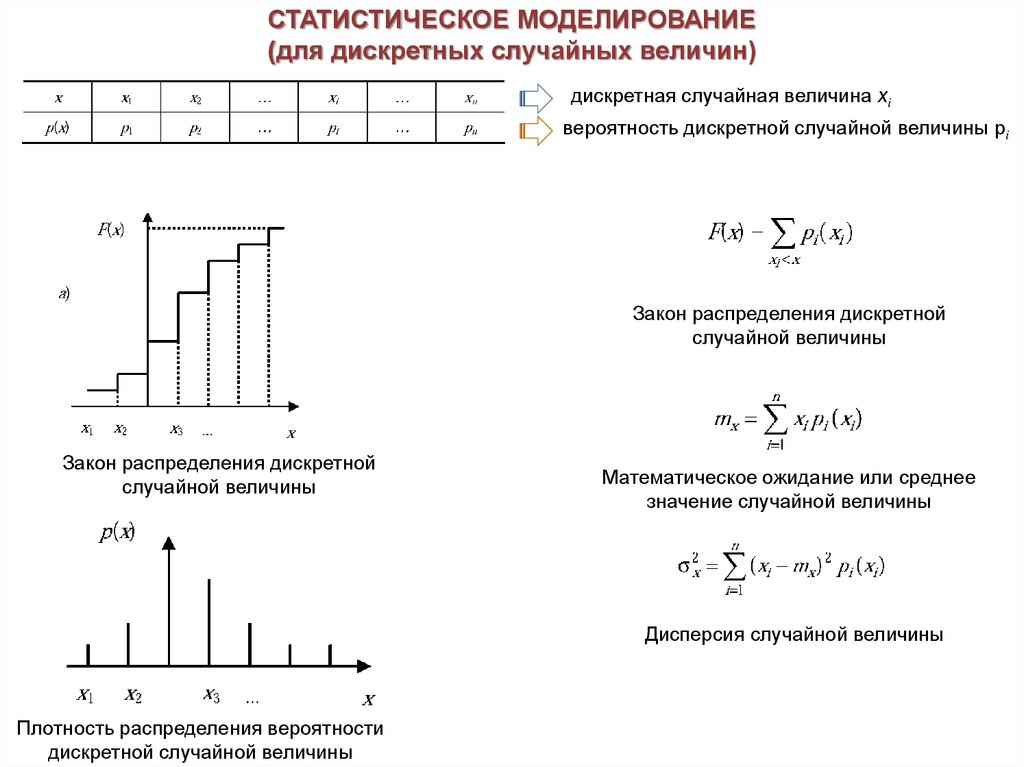
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
(для дискретных случайных величин)
дискретная случайная величина хi
вероятность дискретной случайной величины pi
Закон распределения дискретной
случайной величины
Закон распределения дискретной
случайной величины
Математическое ожидание или среднее
значение случайной величины
Дисперсия случайной величины
Плотность распределения вероятности
дискретной случайной величины

36.

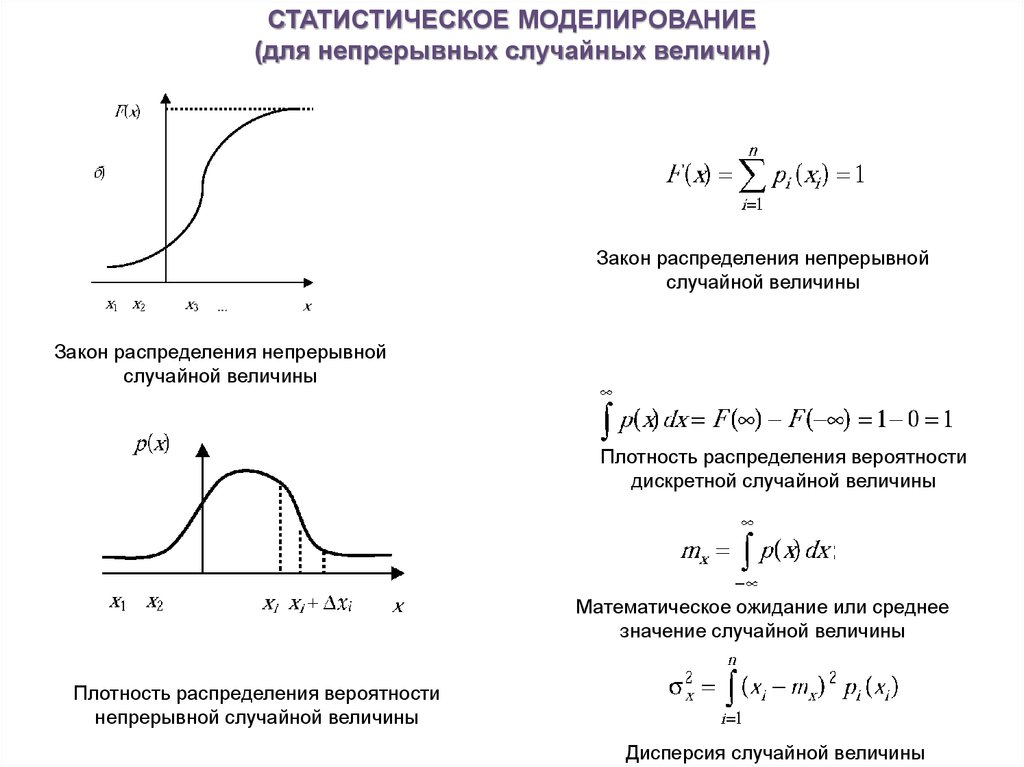
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
(для непрерывных случайных величин)
Закон распределения непрерывной
случайной величины
Закон распределения непрерывной
случайной величины
Плотность распределения вероятности
дискретной случайной величины
Математическое ожидание или среднее
значение случайной величины
Плотность распределения вероятности
непрерывной случайной величины
Дисперсия случайной величины

37.

АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Процессы функционирования системы записываются в виде некоторых функциональных соотношений:
алгебраических, дифференциальных, интегральных уравнений.
Аналитическая модель может быть исследована следующими методами:
1) аналитическим, когда стремятся получить в общем виде явные зависимости для характеристик систем;
2) численным, когда не удается найти решение уравнений в общем виде и их решают для конкретных
начальных данных;
3) качественным, когда при отсутствии решения находят некоторые его свойства.

38.

ТЕОРЕТИКО-МНОЖЕСТВЕННОЕ ПРЕДСТАВЛЕНИЕ
Понятия: множество, элементы множества, отношения на множествах.
Понятие множество относится к числу интуитивно постигаемых понятий, которым трудно дать
определение.
Это понятие содержательно эквивалентно понятиям «совокупность», «собрание», «ансамбль»,
«коллекция», «семейство», «класс» и другим обобщающим понятиям.
Множества могут задаваться следующими способами:
1. Списком, перечислением (интенсиональным путём);
или
2. Путём указания некоторого характеристического свойства А (экстенсионально).
Например, «множество натуральных чисел», «множество рабочих данного завода», «множество
планет солнечной системы», «множество А» и т.д.
или
свертывание

39.

МНОЖЕСТВО И ПОДМНОЖЕСТВО
Схема представлений
теоретико-множественных моделей
Пустое множество - множество, в котором в данный момент нет ни одного элемента: D=Ø.

40.

ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ