Четыре способа построения графиков

1.

Не боги горшки обжигают
Математика не так страшна
Как ею пугают

2. Четыре способа построения графиков

1)На основании определения модуля.
2) С помощью геометрических преобразований
графиков.
3)Метод вершин
4) Путём сложения ординат графиков функций
соответствующих одним и тем же абсциссам

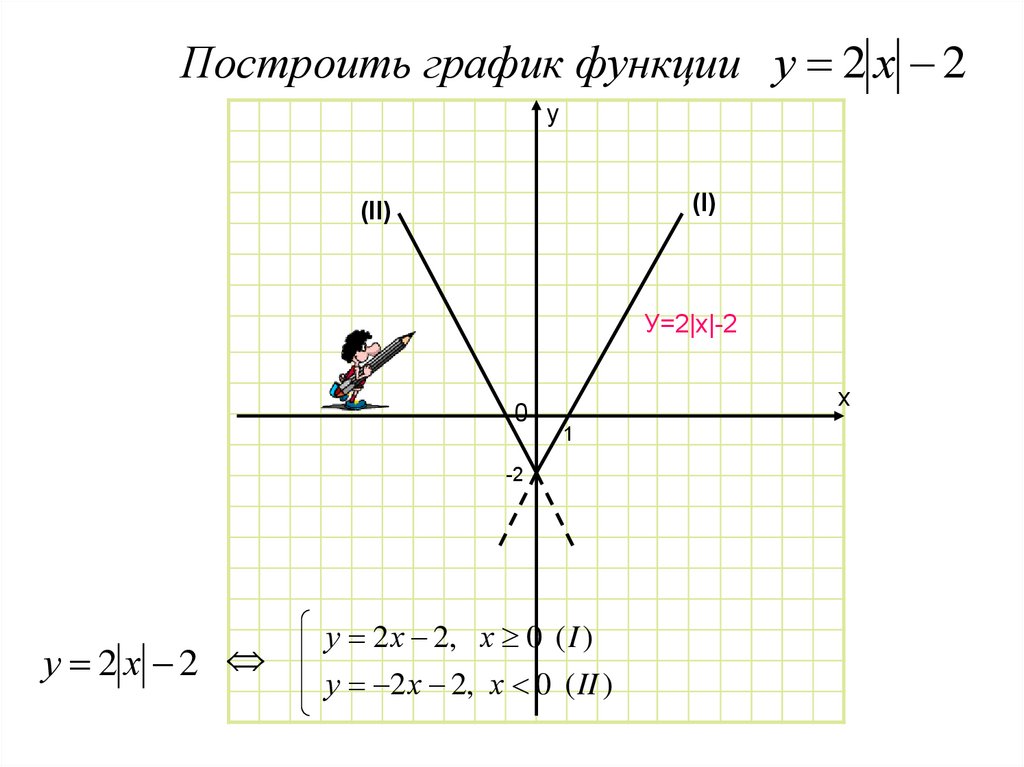
3. Построить график функции

у 2 х 2
у
(I)
(II)
У=2|х|-2
0
х
1
-2
у 2х 2
у 2 х 2, х 0 ( I )
у 2 х 2, х 0 ( II )

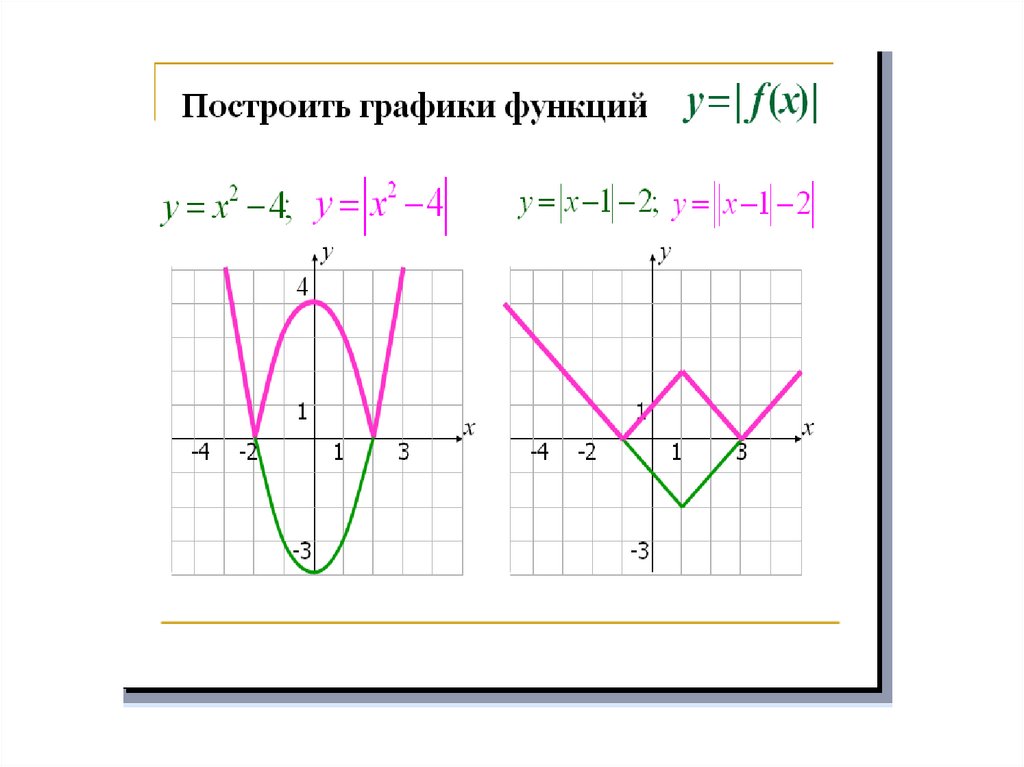
4. Построение графика функции у=|f(x)|.

f (x)
f ( x), при f ( х) 0,
f ( x), при f ( х) 0.
Получаем алгоритм построения графиков
функции у f (x) .
1. Строим график функции f (х) .
2. Часть графика у f (x) , лежащая над осью ОХ,
сохраняется, часть его, лежащая под осью ОХ,
отображается симметрично относительно оси ОХ.

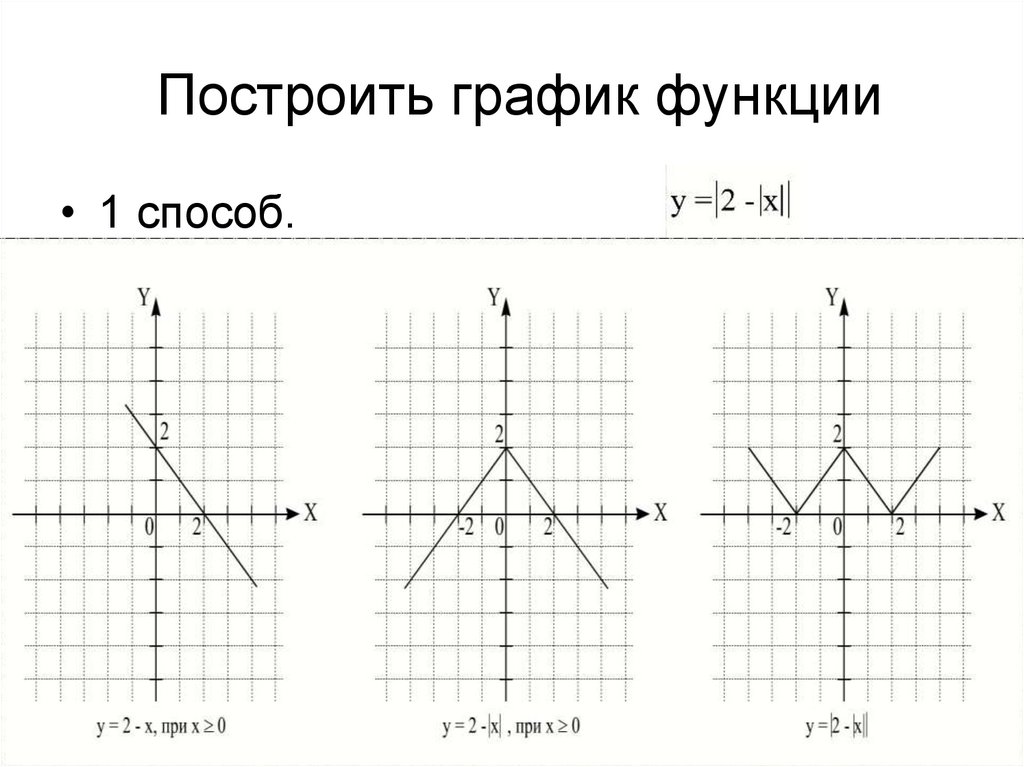
5. Построить график функции

• 1 способ.

6.

7. График функции

у f1 ( x) f 2 ( x) ... f n ( x)
Графиком непрерывной кусочно-линейной функцией является
ломаная линия с двумя бесконечными крайними звеньями.
1-ый способ: на основании определения модуля.
у x 1 x 3
Пример:
числовую ось на 3 промежутка.
1. x ≤ 1 y=1-x+3-x=4-2x
2. 1≤x ≤3 y=x-1+3-x=2
3. x>3 y=x-1+x-3=2x-4
Точки x=1 и x=3 разбивают

8.

у = |х - а| + |х - в|.
k=-2
k=2
b-a
x
a
b
«Корыто»

9.

y
4
2
1
-1
3
x

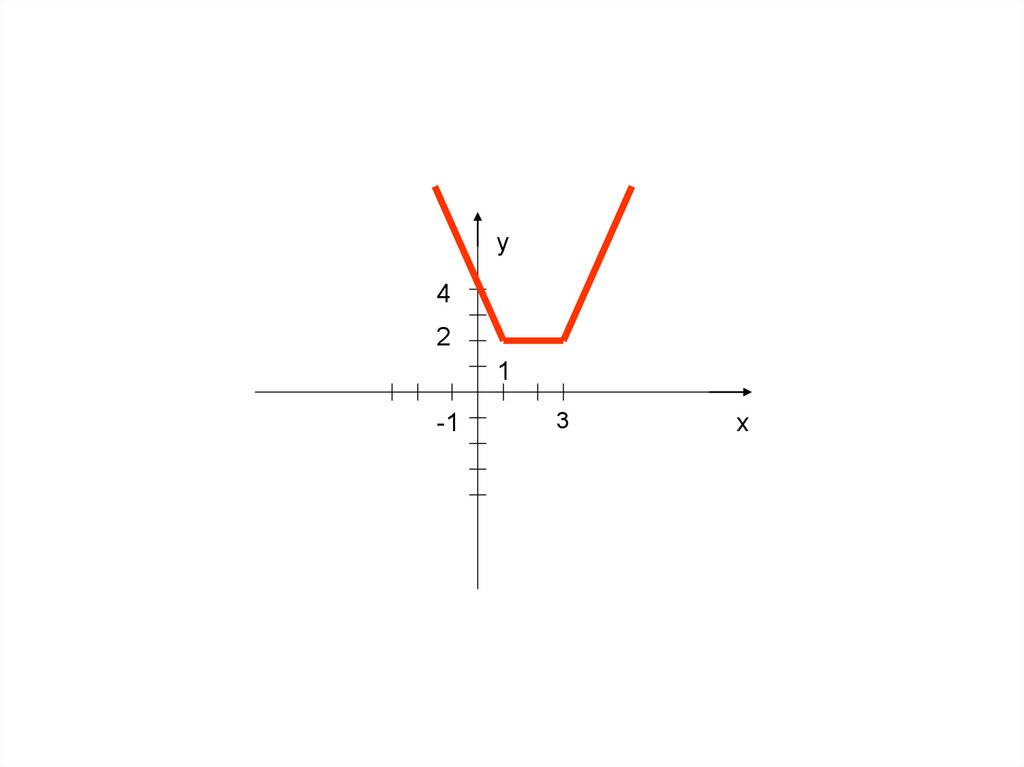
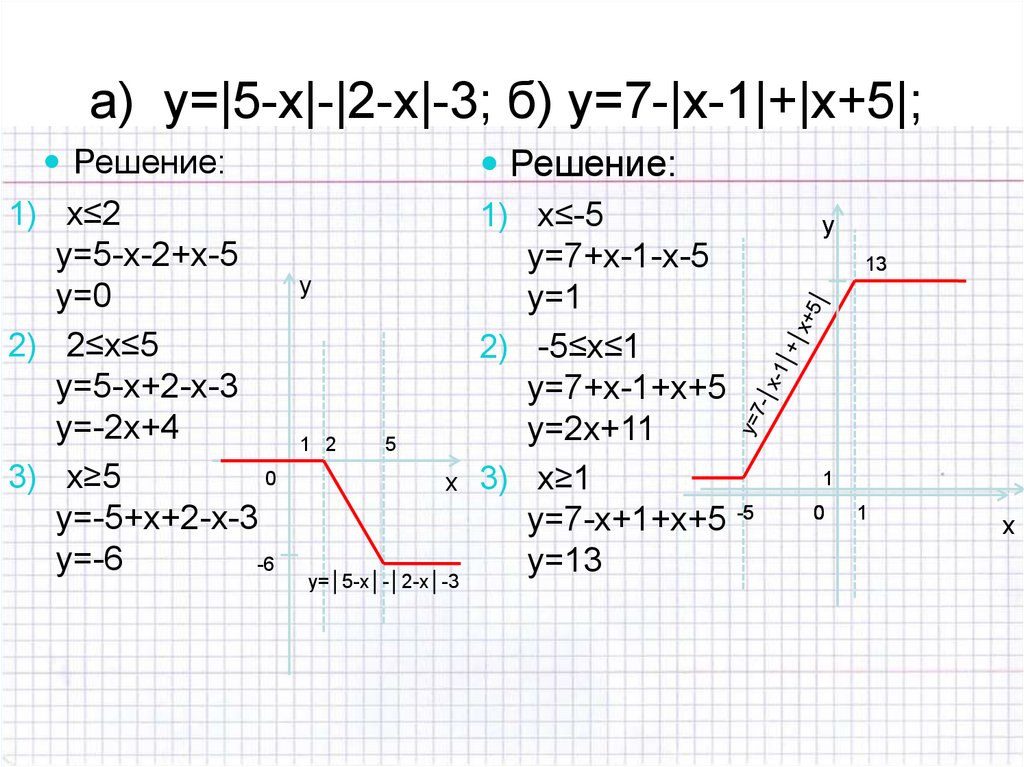
10. а) y=|5-х|-|2-х|-3; б) y=7-|х-1|+|х+5|;

Решение:
1) х≤2
y=5-х-2+х-5
y=0
2) 2≤х≤5
y=5-х+2-х-3
y=-2х+4
0
3) x≥5
y=-5+х+2-х-3
y=-6
-6
y
1 2
5
x
y=│5-x│-│2-x│-3
Решение:
1) х≤-5
y=7+х-1-х-5
y=1
2) -5≤х≤1
y=7+х-1+х+5
y=2х+11
3) x≥1
y=7-х+1+х+5 -5
y=13
y
13
1
0
1
x

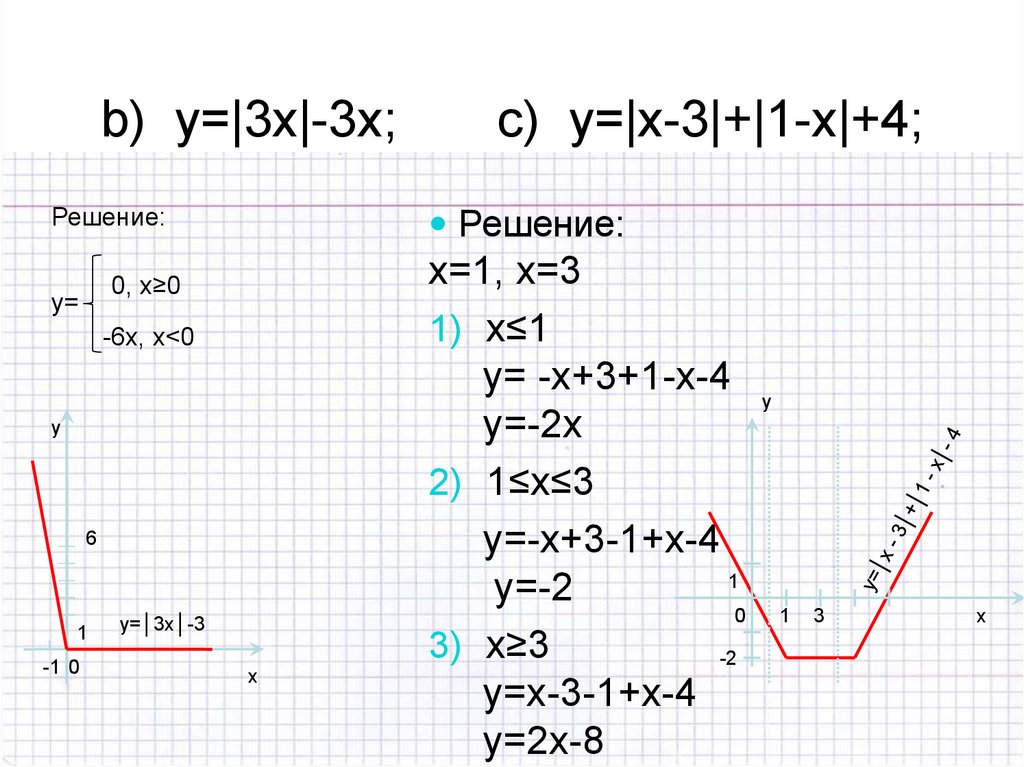
11. b) y=|3х|-3х; c) y=|х-3|+|1-х|+4;

b) y=|3х|-3х;
Решение:
Решение:
0, х≥0
y=
-6х, х<0
y
6
1
-1 0
c) y=|х-3|+|1-х|+4;
y=│3x│-3
x
х=1, х=3
1) x≤1
y= -x+3+1-x-4
y=-2x
2) 1≤x≤3
y=-x+3-1+x-4
1
y=-2
0
3) x≥3
-2
y=x-3-1+x-4
y=2x-8
y
1
3
x

12. График функции

13. Преобразование графиков функций. Графики функций, содержащих модуль.

у
y = f(x)
график исходной
функции
y =|f(x)|
y = f(x)
0
х
y =|f(x)|
часть графика,
лежащая над осью Ох,
сохраняется, часть,
лежащая ниже оси Ох,
симметрично
отображается
относительно оси Ох

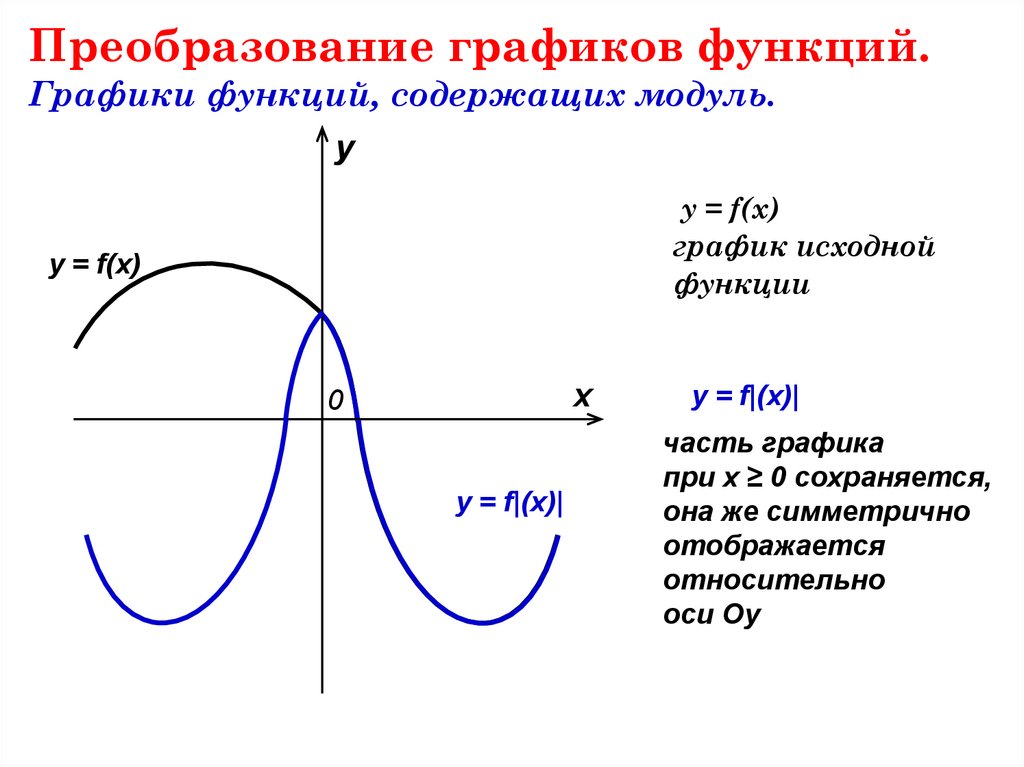
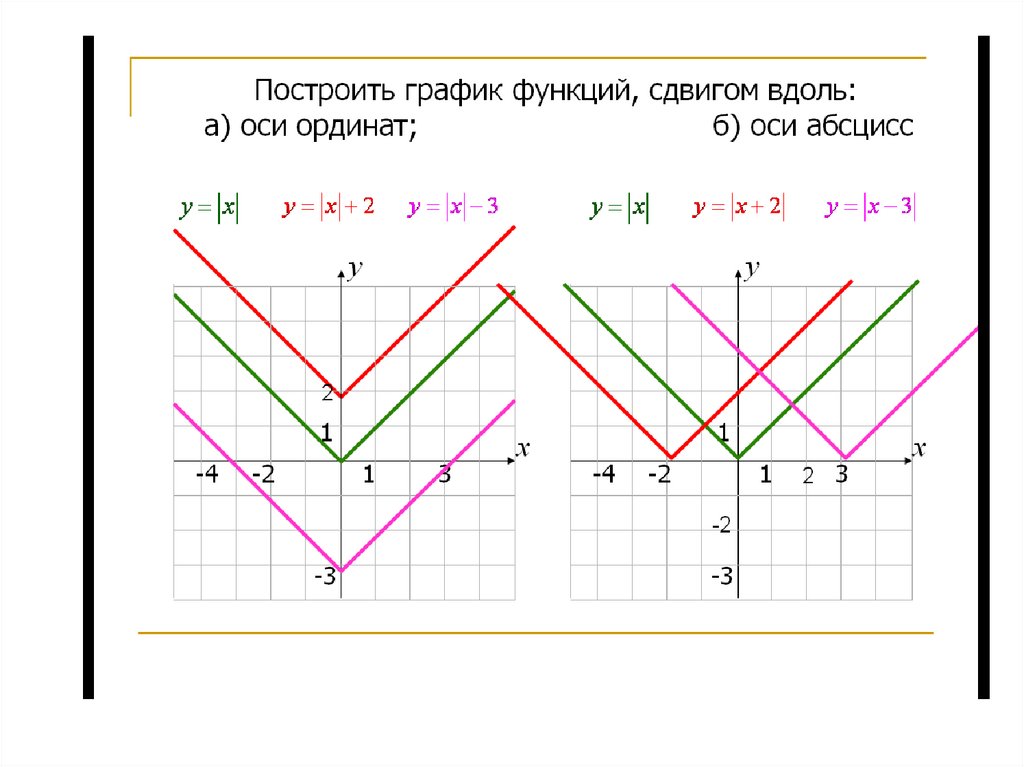
14. Преобразование графиков функций. Графики функций, содержащих модуль.

у
y = f(x)
график исходной
функции
y = f(x)
х
0
y = f|(x)|
y = f|(x)|
часть графика
при х ≥ 0 сохраняется,
она же симметрично
отображается
относительно
оси Оу

15. Если в модуль берется аргумент функции, график будет симметричен относительно оси ординат. Если в модуль берутся значения

Если в модуль берется аргумент
функции, график будет симметричен
относительно оси ординат.
y f
x
Если в модуль берутся значения функции,
график будет симметричен относительно
оси абсцисс.
y f x
Если в модуль берется все уравнение,
выражающее функцию, график
отражается в верхнюю полуплоскость
относительно оси абсцисс.
29.01.2024 16:57
y f x
15

16.

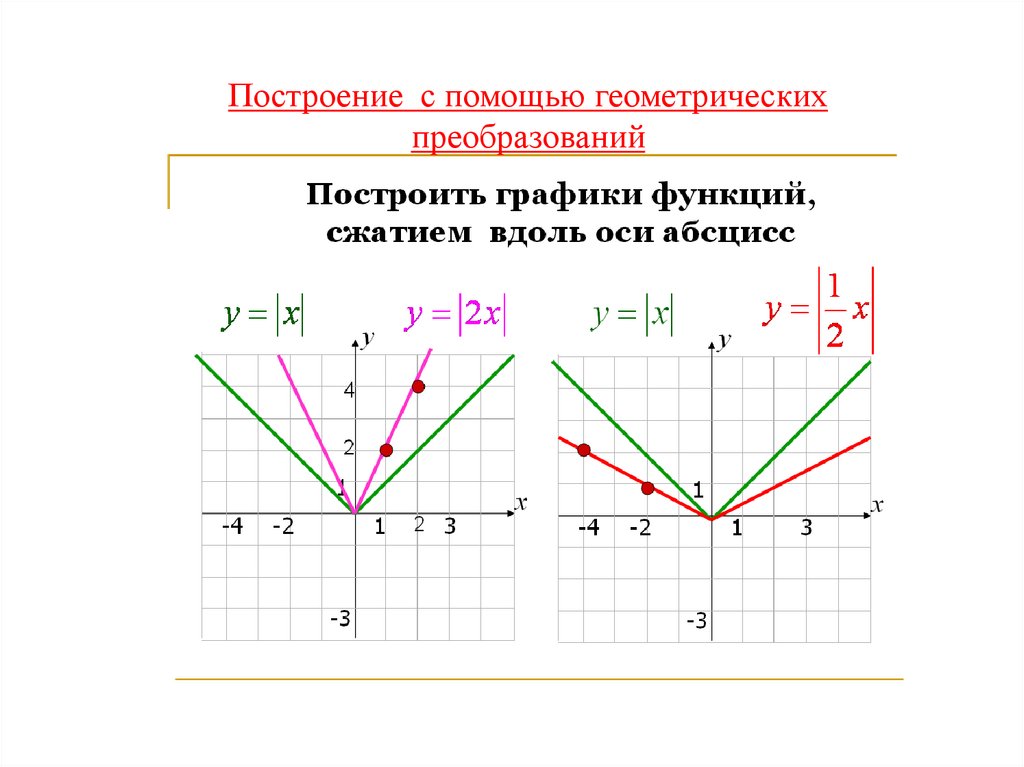
Построение с помощью геометрических
преобразований

17.

18.

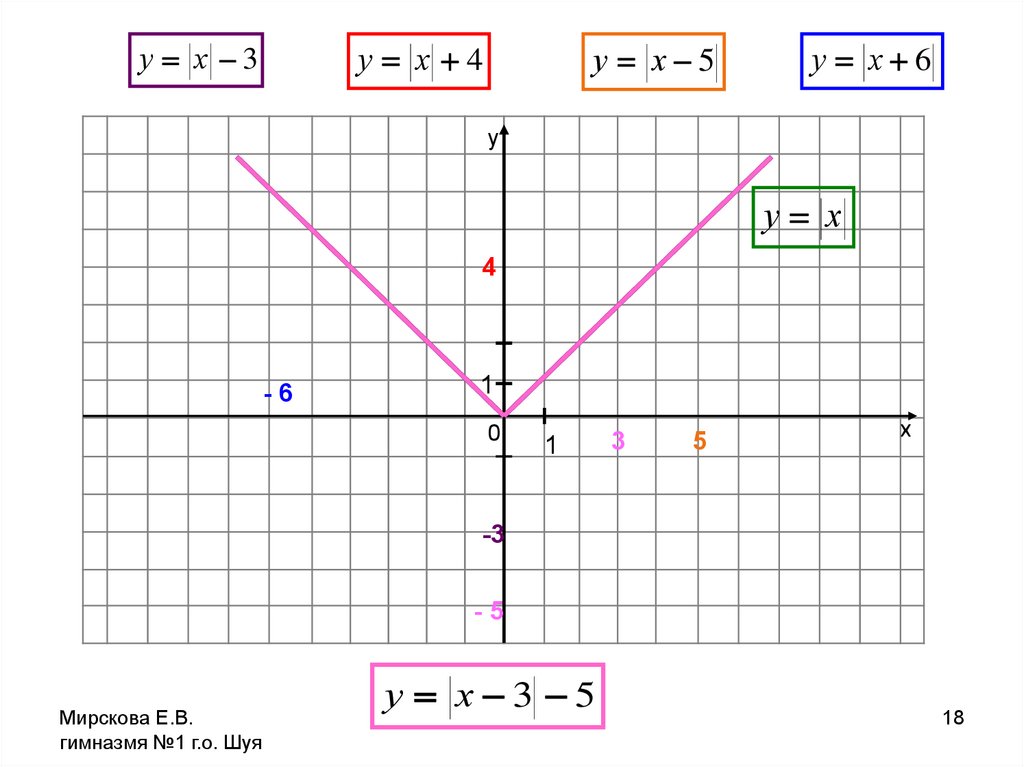
у х 3
у х 4
у х 5
у х 6
у
у х
4
-6
1
0
1
3
5
х
-3
-5
Мирскова Е.В.
гимназмя №1 г.о. Шуя
у х 3 5
18

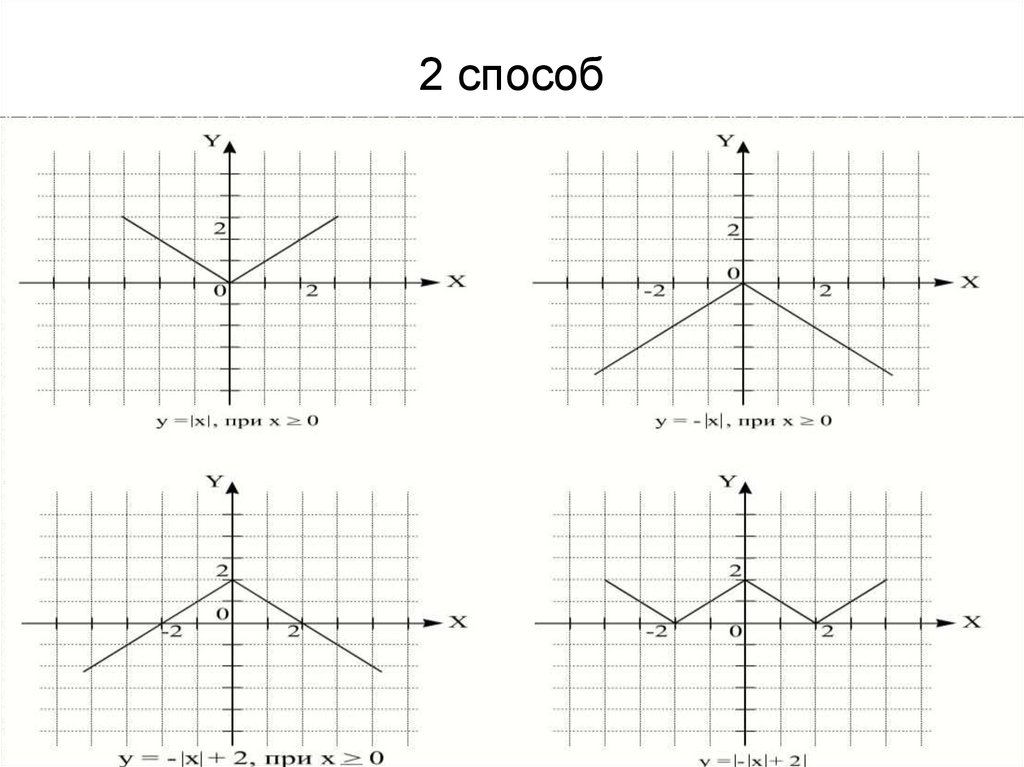
19. 2 способ

20.

21.

У₁= |х|
у₂=|х-1|
у₃= у₂-2
у₄= |у₃|
У=||х-1|-2|

22.

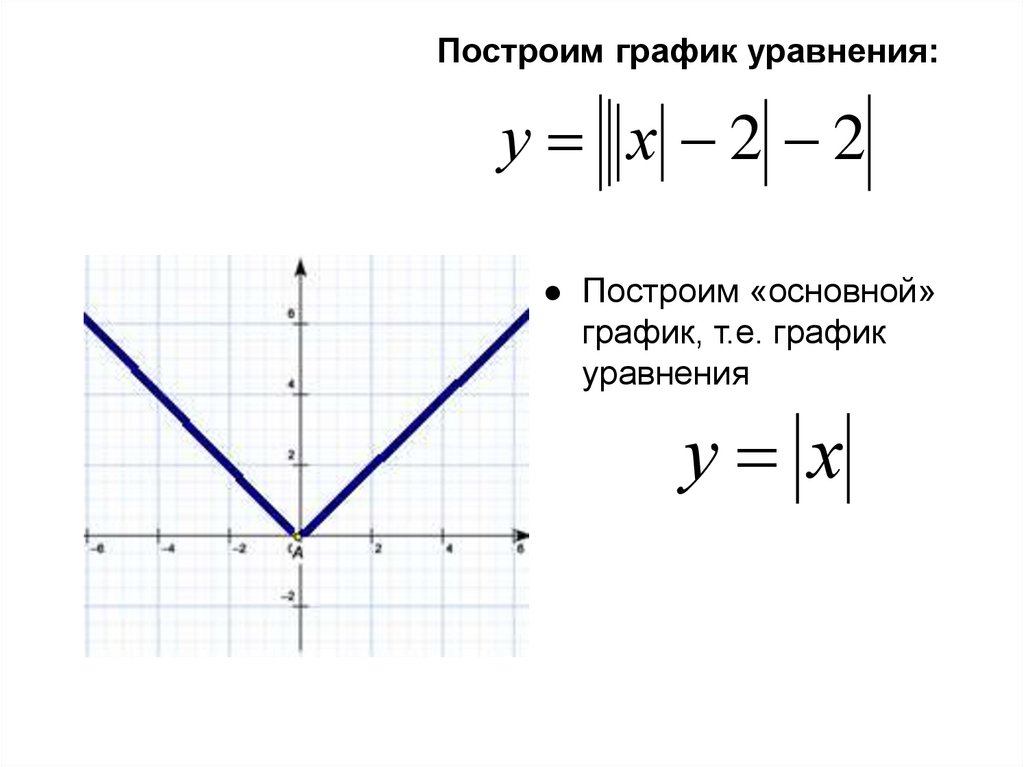
Построим график уравнения:
у х 2 2
Здесь при построении графика
удобно использовать сдвиги
вдоль осей координат. Будем
действовать по следующему
плану:

23.

Построим график уравнения:
у х 2 2
Построим «основной»
график, т.е. график
уравнения
у х

24.

Построим график уравнения:
у х 2 2
• Сдвинем построенный
график на 2 единицы
вниз; получится
график уравнения
у х 2

25.

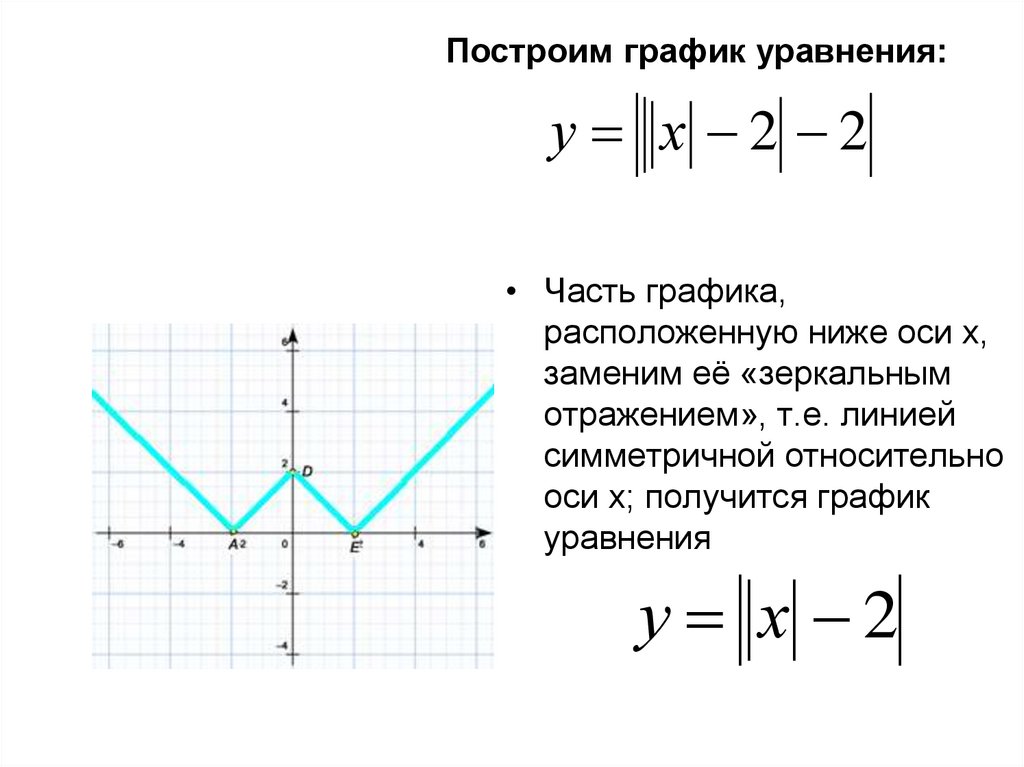
Построим график уравнения:
у х 2 2
• Часть графика,
расположенную ниже оси х,
заменим её «зеркальным
отражением», т.е. линией
симметричной относительно
оси х; получится график
уравнения
у х 2

26.

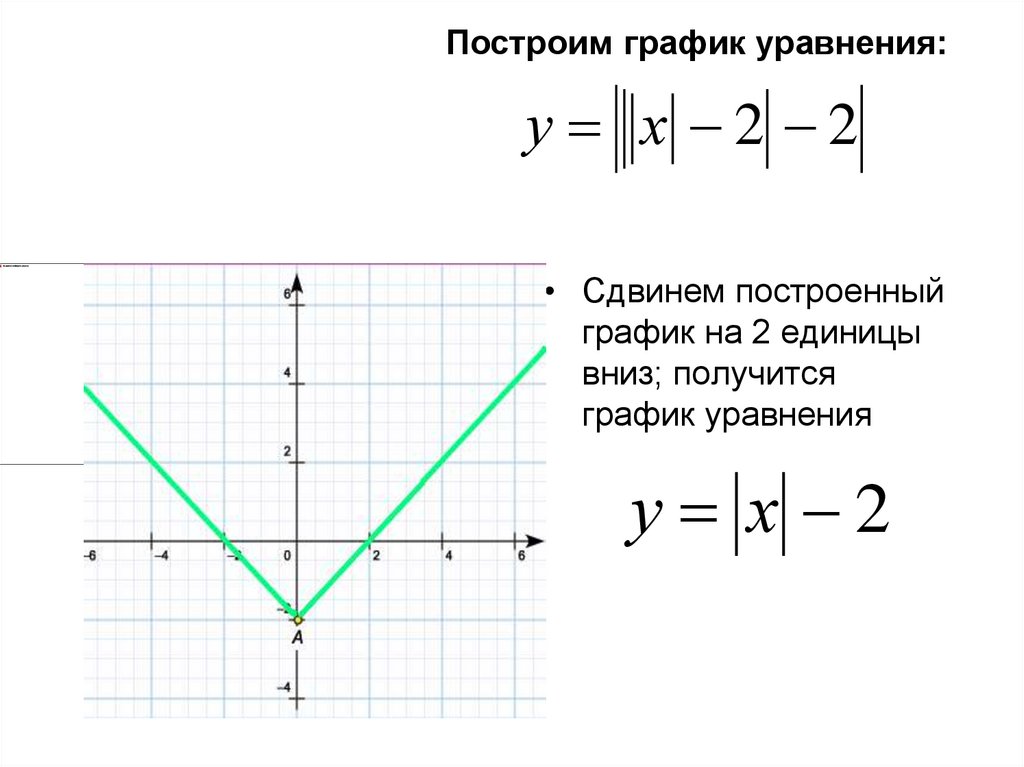
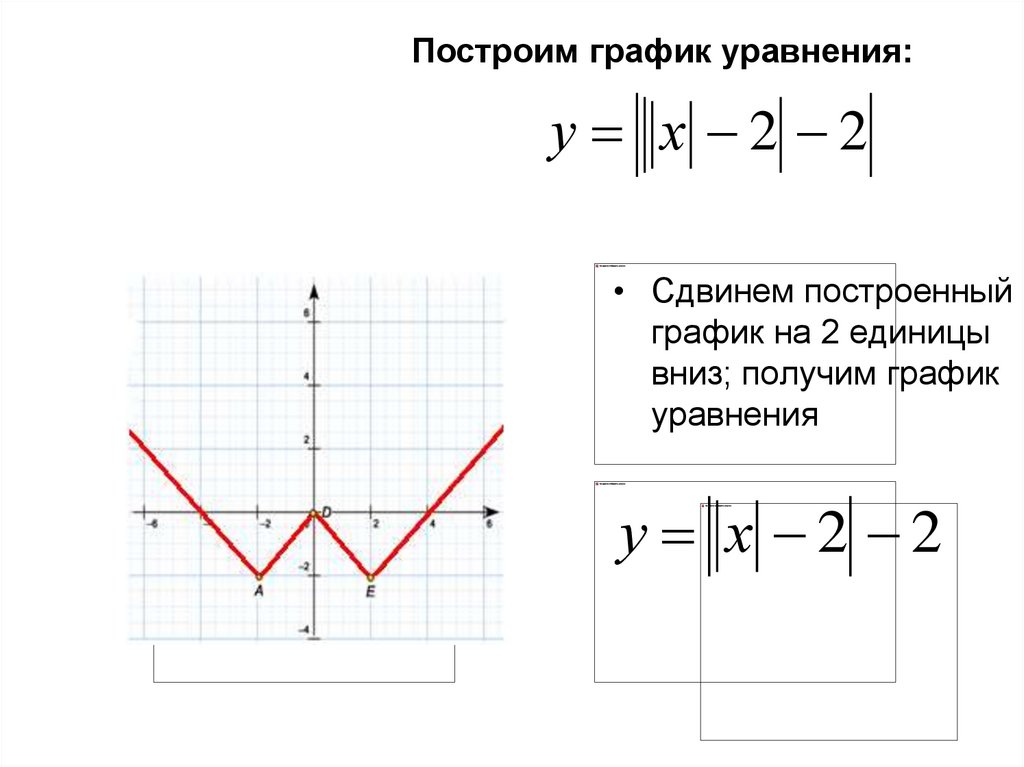
Построим график уравнения:
у х 2 2
у х 2 2
• Сдвинем построенный
график на 2 единицы
вниз; получим график
уравнения
у х 2 2

27.

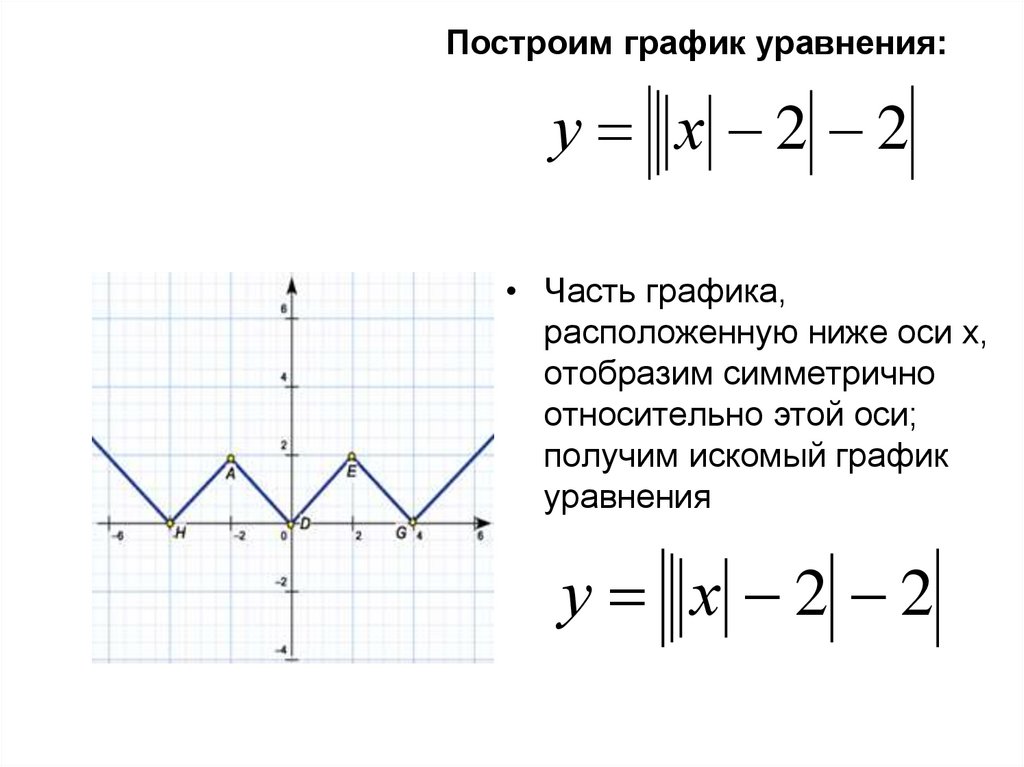
Построим график уравнения:
у х 2 2
• Часть графика,
расположенную ниже оси х,
отобразим симметрично
относительно этой оси;
получим искомый график
уравнения
у х 2 2

28.

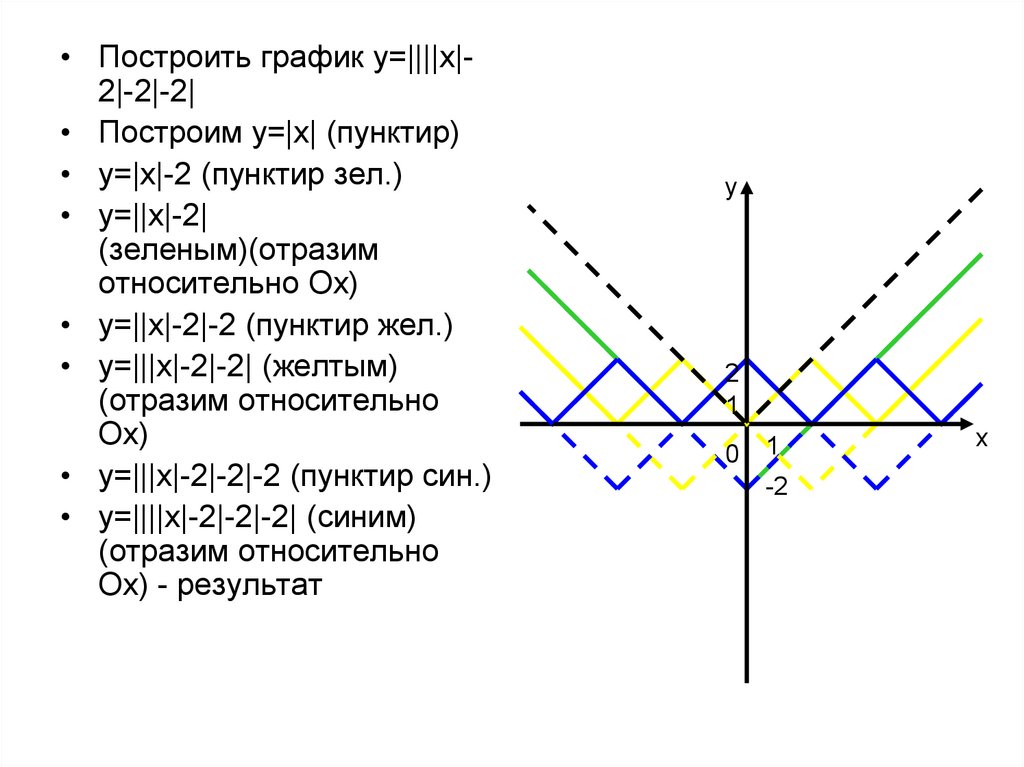
• Построить график y=||||x|2|-2|-2|
• Построим y=|x| (пунктир)
• y=|x|-2 (пунктир зел.)
• y=||x|-2|
(зеленым)(отразим
относительно Ох)
• y=||x|-2|-2 (пунктир жел.)
• y=|||x|-2|-2| (желтым)
(отразим относительно
Ох)
• y=|||x|-2|-2|-2 (пунктир син.)
• y=||||x|-2|-2|-2| (синим)
(отразим относительно
Ох) - результат
y
2
1
0
1
-2
x

29.

y=Ix+3I
y=IxI+3
y=-2IxI-2
y=6-Ix-5I
y=1/3Ix-6I-3

30. 3 способ. Метод вершин

Алгоритм:
1.находим нули подмодульных выражений.
2.Составим таблицу, в которой кроме этих
нулей записывается по одному целому
значению х слева и справа от них.
3.Наносим эти точки на координатной
плоскости и соединяем последовательно,
точки перелома и есть вершины ломаной.

31.

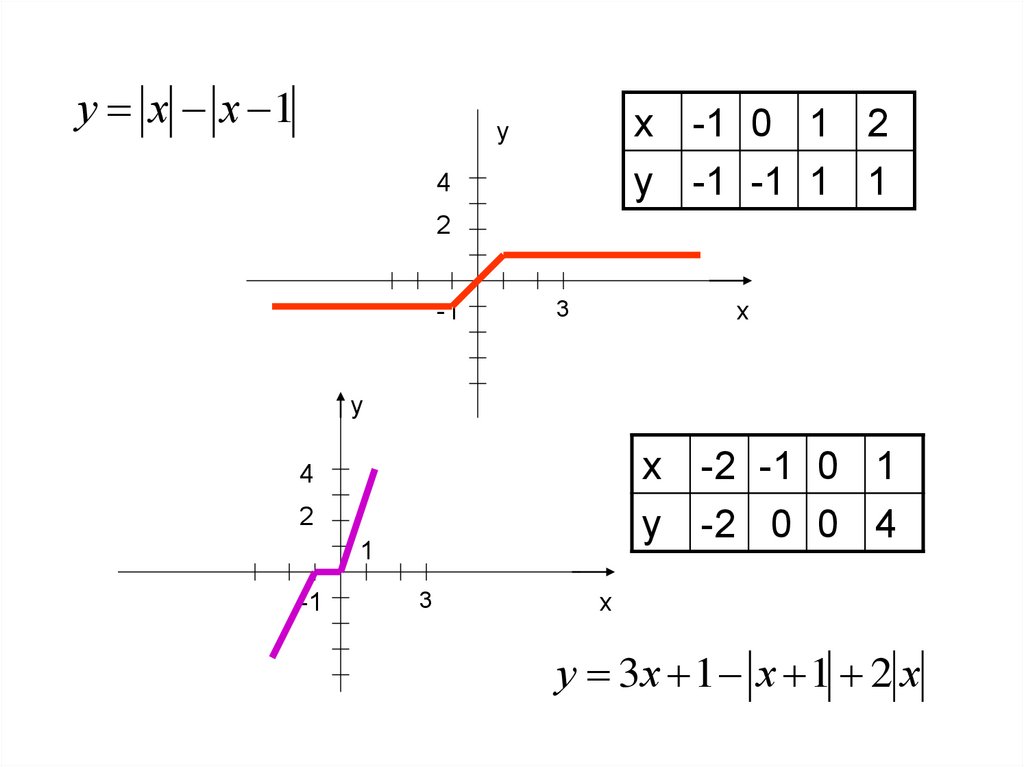
у х х 1
х -1 0 1 2
у -1 -1 1 1
y
4
2
-1
3
x
у
х -2 -1 0 1
у -2 0 0 4
4
2
1
-1
3
x
у 3х 1 х 1 2 х

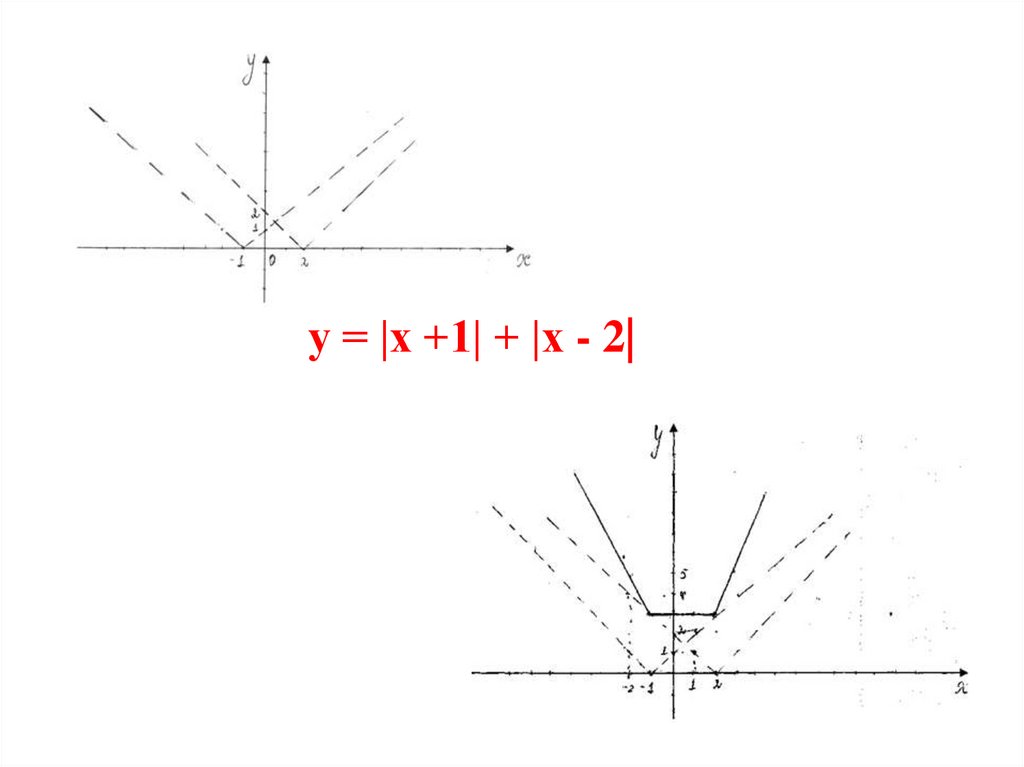
32. 4 способ. Путём сложения ординат графиков функций соответствующих одним и тем же абсциссам Пример: y=|x+1|+|x-2|

у
3
Y=|x+1|
Y=|x-2|
0
-1
х
2

33.

у = |х +1| + |х - 2|

34.

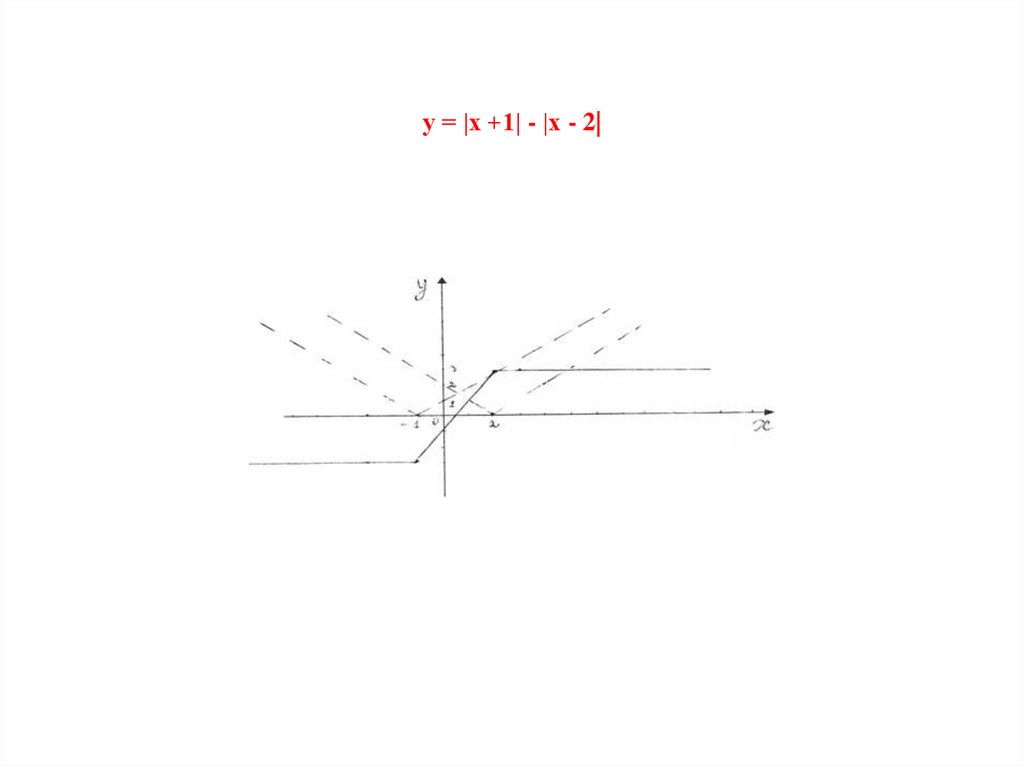
у = |х +1| - |х - 2|

35.

Постройте графики функции
у =|х-4|+|х+4|
у=|х+3|-|х-1|