Модель Леонтьева

1.

МОДЕЛЬ ЛЕОНТЬЕВА

2.

Пусть весь производственный сектор народного
хозяйства разбит на n чистых отраслей.
Чистая
отрасль
–
условное
понятие
(экономическая абстракция) – некоторая часть
народного хозяйства, относительно цельная.
Например, электроэнергетика (совокупность
электростанций,
независимо
от
их
ведомственной
принадлежности),
машиностроение, с/х и т.п.

3.

Будем считать, что каждая отрасль выпускает
продукт только одного типа и разные отрасли
выпускают разные продукты. Таким образом,
в рассматриваемой нами производственноэкономической системе выпускается n видов
продуктов.
В процессе производства своего вида продукта
каждая отрасль нуждается в продукции других
отраслей.

4.

Пусть в некоторый момент времени (в году Т0)
составлен балансовый отчет по народному
хозяйству по следующей форме:
№
отрасли
1
2
…
n
Валовый
выпуск
Конечное
потребление
1
…
производит 1-я
отрасль
2
…
производит 2-я
отрасль
…
n
…
…
…
…
…
…
…
производит n-я
отрасль

5.

- количество продукции i-ой отрасли,
израсходованное j-ой отраслью;
- общий объем продукции (валовой выпуск)
i-ой отрасли;
- продукция i-ой отрасли, не потребленная
другими отраслями, пошедшая на создание
запасов, потребленная во внепроизводственной
сфере.
или

6.

Единицы измерения указанных величин
либо натуральные, либо стоимостные. В
зависимости
от
этого
различают
натуральный,
либо
стоимостной
межотраслевой баланс.
Перейдем к безразмерным величинам,
разделив все элементы i-ой строки на .
- относит. количество единиц
продукции
i-ой
отрасли,
необходимое для производства единицы
продукции j-ой отрасли.

7.

- доля продукции i-ой отрасли,
пошедшая на непроизводственное
потребление.
Числа
называют коэффициентами прямых
затрат
или
технологическими
коэффициентами,
они
характеризуют
технологию отраслей (народного хозяйства).

8.

Матрица
(матрица прямых затрат или
технологическая
матрица)
характеризует
структуру
межотраслевых
связей,
существующую технологию общественного
производства.
Сравнивая такие матрицы в разные моменты
времени, можно проследить направление
изменения развития технологий в стране.
Еще
более
интересные
возможности
открываются при использовании матрицы А
для текущего и долгосрочного планирования и
прогнозирования.

9.

Сделаем 2 предположения:
сложившуюся
технологию
производства
считаем неизменной в рассматриваемом
промежутке времени, т.е. матрица А
постоянна;
линейность существующей технологии, т.е.
для производства хj единиц продукции j-ой
отрасли необходимы затраты
продукции
i-ой отрасли.

10.

Таким
образом,
матрица
А
описывает
технологию при единичной интенсивности
работы всех отраслей.
Пусть Х=(х1,х2,…,хn) – вектор объемов
производства
в
отраслях
(вектор
интенсивности), т.е. i-ая отрасль работает с
интенсивностью хi. Тогда,
– это потребленные объемы
продукции по отраслям для
производства Х. Вне производства остается
C=X-AX (*).

11.

Основной
вопрос,
возникающий
при
планировании производства: при заданном
векторе потребности
непроизводственной
сферы определить необходимый вектор Х
валового выпуска. Очевидно, что с учетом
этой интерпретации, этот вектор должен быть
больше либо равный нулю.
Уравнение
(*)
с
учетом
изложенной
интерпретации матрицы А и векторов Х и С
называют моделью Леонтьева.

12.

Продуктивность модели
Леонтьева

13.

Определение. Модель Леонтьева, задаваемая
технологической матрицей A, продуктивна,
если для любого неотрицательного вектора
конечного
спроса
С
существует
неотрицательный вектор X, такой, что
В этом случае технологическая матрица A также
называется продуктивной.

14.

Теорема 1.
Матрица
продуктивна тогда и только
тогда, когда существует матрица
Доказательство.
Необходимость. Пусть матрица A неотрицательна и
продуктивна. Рассмотрим столбцы единичной матрицы.

15.

Возьмём в качестве вектора
.
Так как матрица A продуктивна, то матричное
уравнение
имеет неотрицательное
решение. Пусть это решение
.
Возьмем в качестве вектора
. Тогда решением
будет
.
И так далее. При
решением будет
.
Таким образом мы получим матрицу
размерности nxn.
Что и требовалось доказать.

16.

Достаточность.
Пусть существует
Докажем, что матрица A продуктивна.
Возьмём любой неотрицательный вектор C.
Рассмотрим
Тогда
Элементы матриц
и C неотрицательны.
Тогда элементы X неотрицательны. Получается,
что для любого неотрицательного С нашелся
неотрицательный X :
Значит,
А – продуктивна. Что и требовалось доказать.

17.

Пример 1.
Продуктивна или нет следующая матрица:
Решение:

18.

Матрица A продуктивна.

19.

Пример 2.
Даны вектор непроизводственного потребления
и матрица межотраслевого баланса
Найти
вектор
валового
выпуска,
обеспечивающий данный вектор потребления.

20.

Решение:

21.

Ответ:

22.

Лемма
Если ряд матриц
сходится, то его сумма будет равна
Доказательство.
Пусть данный ряд сходится, тогда
(необходимое условие сходимости ряда).
Рассмотрим матричное тождество:
Покажем, что матрица
существует.
.

23.

Предположим противное:
Рассмотрим СЛАУ
(1)
У нее существует бесконечное множество решений,
значит существует ненулевое решение X.
Противоречие (по условию Х ненулевой вектор).
Значит существует матрица

24.

Рассмотрим последовательность частичных сумм
Поэтому
Что и требовалось доказать.

25.

Матрица полученная из единичной некоторой
перестановкой её столбцов называется
перестановочной, т.е. у перестановочной
матрице в каждом столбце одна единица,
остальные нули.
Матрица A называется неразложимой, если не
существует такой перестановочной матрицы
Р, что
где
- квадратные матрицы.

26.

Теорема 2 (Фробениуса-Перрона).
Для любой неразложимой матрицы
существует собственное число
,
(называемое числом Фробениуса матрицы A),
такое, что для любого собственного числа
матрицы А выполняется
,и
существует единственный (с точностью до
множителя) собственный вектор
,
отвечающий собственному числу
(называемый вектором Фробениуса матрицы
A). Причем, если A>0, то
и

27.

- собственное число матрицы А.
- собственный вектор матрицы А,
соответствующий собственному числу .
- характеристический многочлен матрицы А.
Собственные числа матрицы А являются
корнями характеристического многочлена.

28.

Пример:

29.

Для
:

30.

Для
:

31.

Лемма
Для любых векторов x и y размерности n и
любой квадратной матрицы А порядка n
(скалярное произведение).
Доказательство.

32.

Теорема 3.
Матрица
продуктивна
Пример 1.
При каких a>0 матрица A продуктивна?

33.

Решение.

34.

Пример 2.
При каких a матрица A продуктивна?

35.

Теорема 4.
Матрица
продуктивна тогда и только
тогда, когда сходится ряд
Следствие.
Если сумма элементов каждого столбца (строки)
матрицы
строго меньше 1, то матрица А
продуктивна.
Давайте вернемся к примерам 1 и 2.

36.

Матрица полных материальных затрат
Матрица
называется матрицей
полных материальных затрат.

37.

Пример.
Имеется матрица МОБ в отчетном периоде:
1
2
ci
vi
1
200
300
500
1000
2
300
1500
1200
3000
Усл.-чист.
продукция (zi)
500
1200
Затраты труда
(Li)
100
150
ОПФ (Фi)
10000
30000
1700
1700

38.

Задание.
1. Определить коэффициенты прямых и полных
материальных затрат, прямой фондоемкости и
трудоемкости по отраслям.
2. Определить валовый выпуск продукции в
плановом периоде, если конечная продукция
первой отрасли выросла на 10%, а второй
отрасли снизилась на 10%.
3. Составить МОБ в плановом периоде.

39.

Решение.
Напомним, что УЧП=А+ЗП+П=V-M, поэтому
Основное балансовое соотношение:
1.

40.

Коэффициенты
прямой
(показывают затраты труда
продукции данной отрасли):
трудоемкости
на единицу
Коэффициенты прямой фондоемкости:

41.

2.
3.
1
2
ci
vi
1
207,03
278,13
550
1035,1
2
310,54
1390,65
1080
2781,3
Усл.-чист.
продукция (zi)
517,53
1112,52
Затраты труда
(Li)
103,51
139,07
ОПФ (Фi)
10351
27813
1630
1630

42.

43.

44.

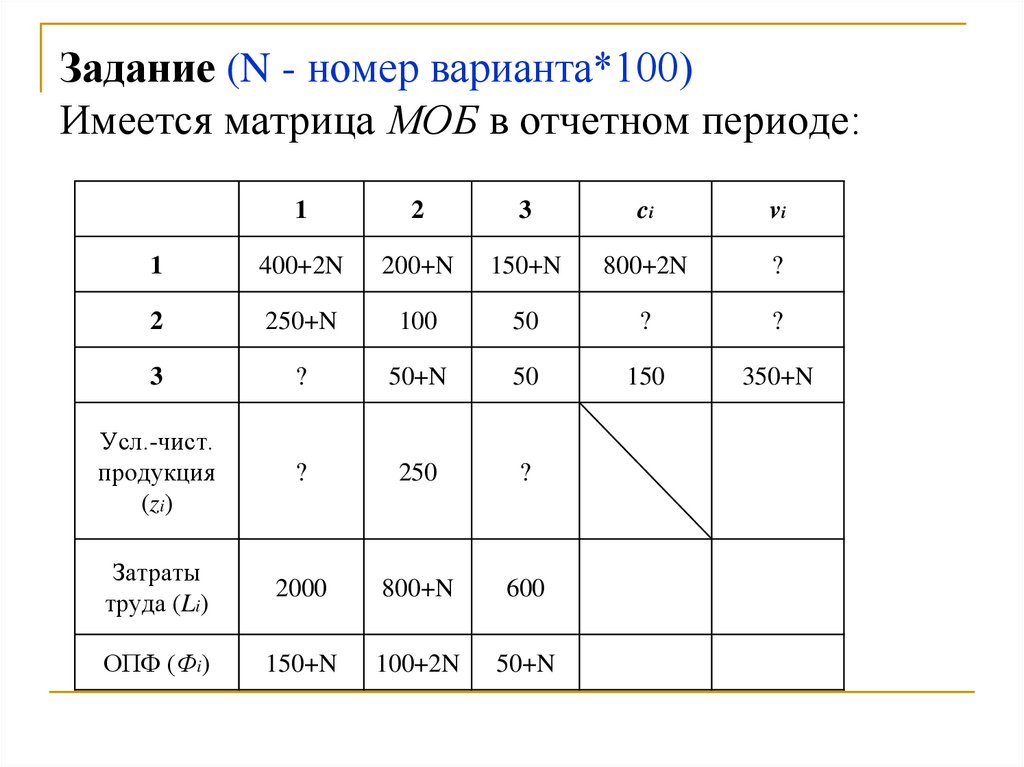
Задание (N - номер варианта*100)
Имеется матрица МОБ в отчетном периоде:
1
2
3
ci
vi
1
400+2N
200+N
150+N
800+2N
?
2
250+N
100
50
?
?
3
?
50+N
50
150
350+N
Усл.-чист.
продукция
(zi)
?
250
?
Затраты
труда (Li)
2000
800+N
600
ОПФ (Фi)
150+N
100+2N
50+N

45.

Задание.
1. Найти недостающие элементы МОБ.
1. Определить коэффициенты прямых и полных
материальных затрат, прямой фондоемкости и
трудоемкости по отраслям.
2. Определить валовый выпуск продукции в
плановом периоде, если конечная продукция
выросла в первой отрасли на 10%, во второй
отрасли на 5%, в третьей отрасли на 3%.
3. Составить МОБ в плановом периоде.