Релятивистская механика

1.

Курс общей физики НИЯУ МИФИ
Добро пожаловать в Физику!
Welcome to Physics!
Zapraszamy do Fizyki!
Fizik`e hoş geldiniz!
Chào mừng bạn đến Vật lý!
Bienvenido a la física!
পদার্বিদযা
থ
স্বাগতম!
Willkommen in Physik!
Лектор: Доцент, кандидат физ.-мат. наук, Андрей ОЛЬЧАК
Lecturer: Andrey OLCHAK, Professor Associate, DSc

2.

Общая Физика
Лекция 13
Механика больших скоростей
(Special Relativity Theory)
Лектор:
доцент НИЯУ МИФИ, к.ф.-м.н.,
Ольчак Андрей Станиславович

3.

С чего начинается физика?
Физика начинается с двух догадок.
1. Покой и движение – понятия не абсолютные, а
относительные. Все зависит от того кто и из какой
системы отсчета наблюдает.
- это принцип относительности, который был вполне осознан
только в XVII веке (Коперник, Галилей, и – в окончательной
формулировке - Ньютон
2. Если наблюдать за движением тела из «правильной»
(инерциальной) системы отсчета, и если на тело не
действуют никакие реальные физические силы, то такое
тело будет двигаться с постоянной по величине и
направлению скоростью, либо покоиться. - это т.н. Первый
закон механики Ньютона.

4.

С чего начинается физика?
ЛОГИЧЕСКИЕ СЛЕДСТВИЯ принципа относительности и Первого
закона механики.
• Состояние покоя = состояние движения с неизменной по величине и
направлению скоростью. Недвижимость (состояние с нулевой
скоростью) ничем физически не отличается от состояния равномерного
прямолинейного движения с НЕ нулевой скоростью
• Все «правильные» наблюдатели (системы отсчета), движущиеся
друг относительно друга равномерно и прямолинейно, физически
равноправны. Во всех «правильных» (инерциальных) системах отсчета
если нет сил – скорость не меняется, а если есть – то меняется.
• Логично предположить, что чем больше сила – тем быстрее меняется
скорость. Это умозаключение выражается формулой
F = mdv/dt

5.

Сложение скоростей.
Преобразования Галилея
Y’
Y
чч:мм:сс
v’ = v - u
V
V’
-u
0’
0
Z’
u
Z
чч:мм:сс
x(t)
x’(t’)
X, X’
x’ = x - ut
t’ = t
x’
t’
1 –u
= 0 1
Матричное умножение - красивая и компактная форма
записи простых и очевидных преобразований Галилея.
Беда в том, что в электродинамике тоже есть формулы
преобразований. Очень похожие, да не совсем…
γ(u) = (1 - u2/c2)-½
1 –u
Ey’
= γ(u) -u/c2 1
Bz’
x
t
Galileo GALILEI
1564-1642
Ey
LORENTZ
с – скорость распространенияHendrik
1853-1928
Bz электромагнитных волн (света)

6.

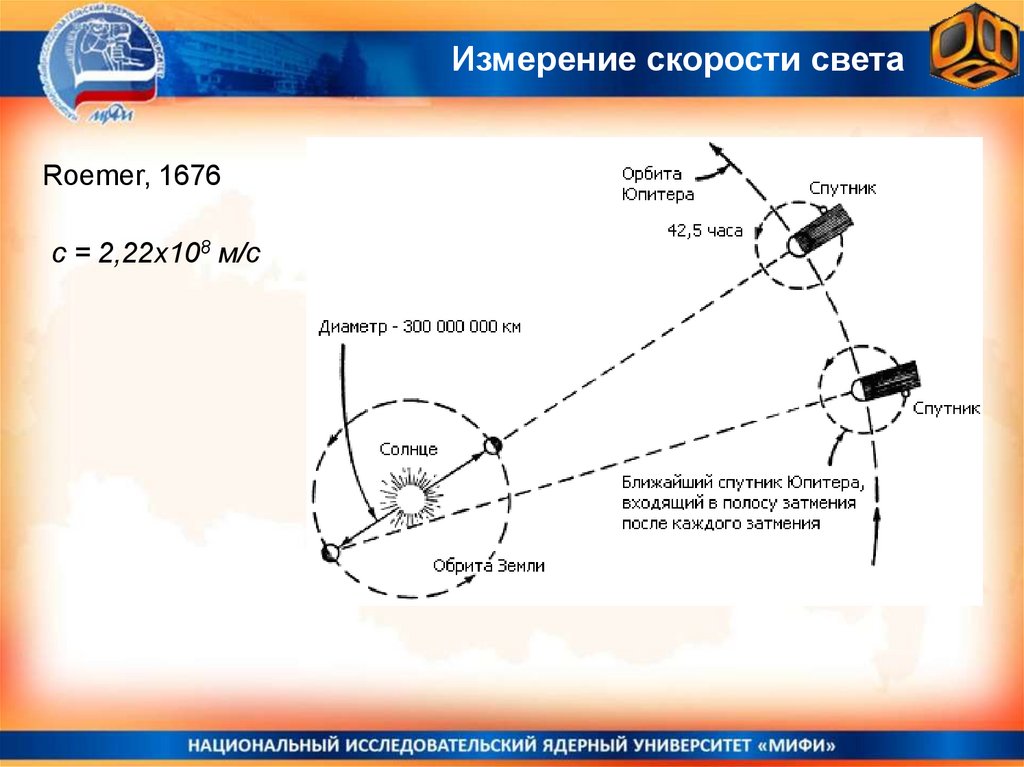
Измерение скорости света
Roemer, 1676
с = 2,22х108 м/с

7.

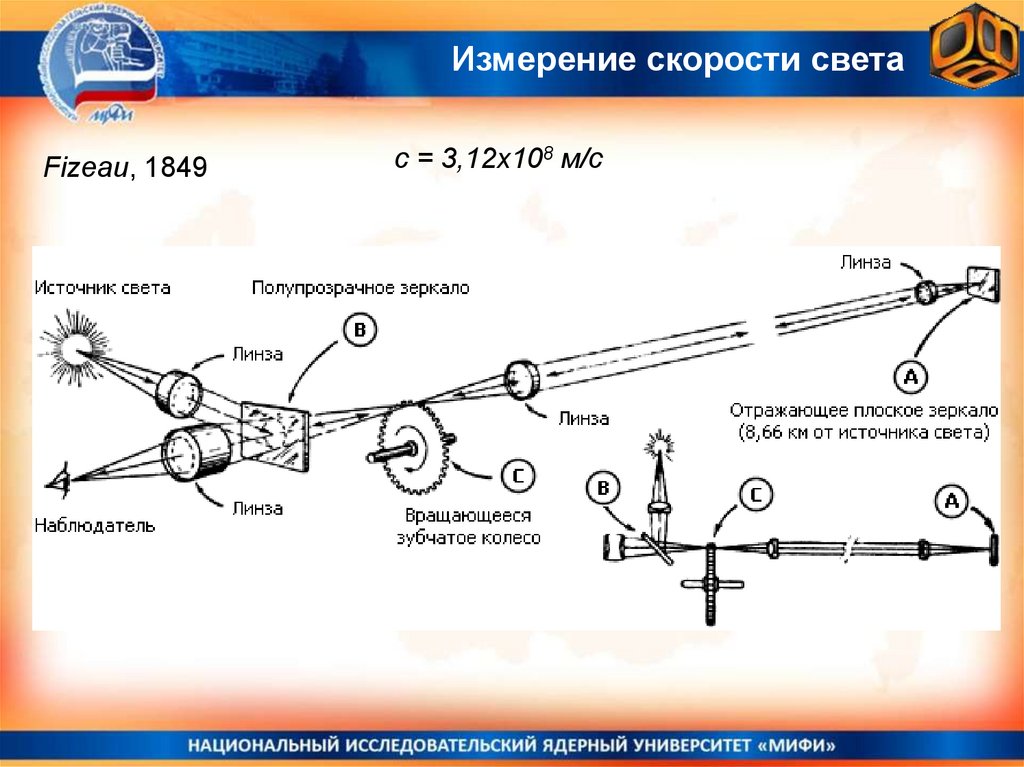
Измерение скорости света
Fizeau, 1849
с = 3,12х108 м/с

8.

Постоянство скорости света
Michelson & Morley, 1887
Опыт Майкельсона-Морли и
последующие опыты Миллера
показали, что скорость света не
зависит ни от направления
движения Земли, ни от
направления распространения
света.
http://www.lightandmatter.com/html_books/6mr/
ch01/ch01.html
А. Майкельсон
Э. Морли

9.

Постоянство скорости света
Опыты Майкельсона-Морли, последующие опыты Миллера, деСиттера, наблюдения двойных звезд показали, что скорость света не
зависит ни от скорости источника, ни от скорости наблюдателя
и всегда равна
с = 3 · 108 м/с
Наиболее точно измеренное значение скорости света в вакууме
(в единицах системы СИ, 1983):
с = 299 792 458 м/с

10.

Сложение скоростей.
Преобразования Галилея и Лоренца
Y’
Y
чч:мм:сс
v’ = v - u
V
V’
-u
0’
0
Z’
u
Z
чч:мм:сс
1 –u
Ey’
= γ(u) -u/c2 1
Bz’
x(t)
x’(t’)
X, X’
x’ = x - ut
t’ = t
x’
t’
1 –u
= 0 1
x
t
Galileo GALILEI
1564-1642
γ(u) = (1 - u2/c2)-½
Ey
с – скорость распространения
Bz электромагнитных волн (света)
В чем проблема» В преобразованиях Галилея нет никаких
ограничений на скорости движения систем отсчета, а у
Лоренца скоростей u>c Быть не может в принципе (!?).
Hendrik LORENTZ
1853-1928

11.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
Y’
Y
0’ 0
Z
u
X, X’
Y
0
Y’
0’
Z
Z’
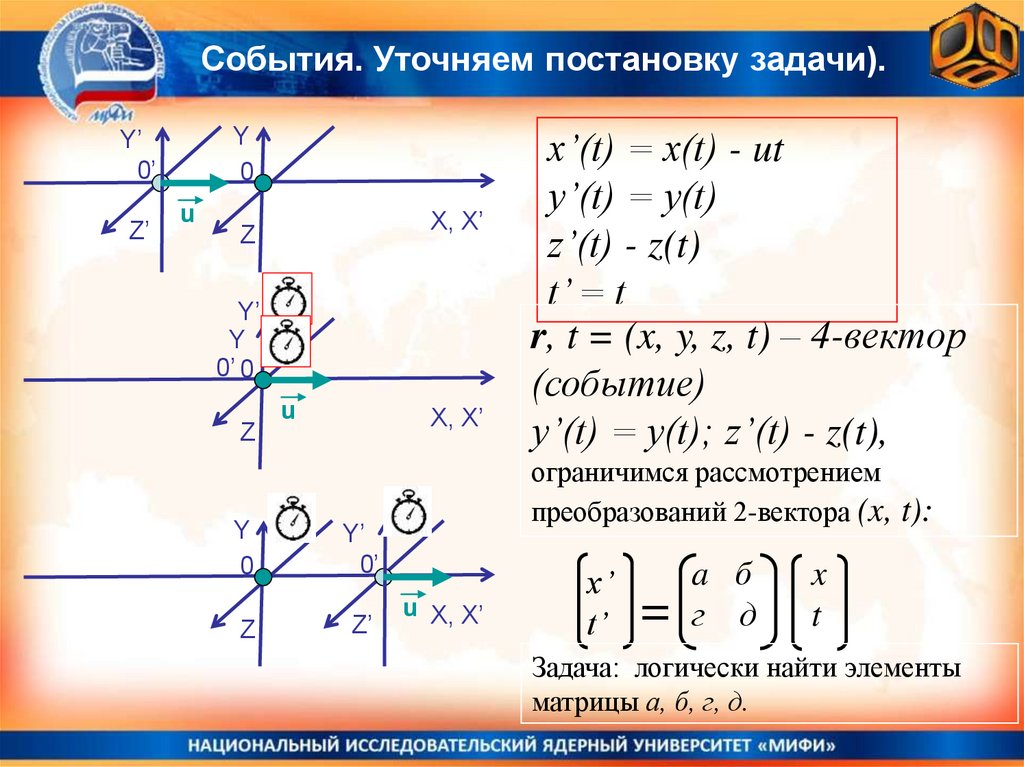
x’(t) = x(t) - ut
y’(t) = y(t)
z’(t) - z(t)
t’ = t
r, t = (x, y, z, t) – 4-вектор
(событие)
y’(t) = y(t); z’(t) - z(t),
ограничимся рассмотрением
преобразований 2-вектора (x, t):
u X, X’
x’
t’
a б
= г д
x
t
Задача: логически найти элементы
матрицы а, б, г, д.

12.

Идея Эйнштейна - Пуанкаре
Идея А. Эйнштейна и А. Пуанкаре (~1905):
Y
применить преобразования типа Лоренца к
механике.
x’
t’
1 –v
= 0 1
x
t
=>
X, X’
0’
0
v
Z
1 –v
x’
=
γ(v)
-v/c2 0
t’
1
Y’
Z’
x(t)
x’(t’)
x
t
γ(v) = (1 - v2/c2)-½
Albert Einstein
1879-1955
Henri Poincare
1854-1912

13.

Идея Эйнштейна - Пуанкаре
Идея А. Эйнштейна и А. Пуанкаре: применить
Y
преобразования типа Лоренца к механике.
x’
t’
1 –v
= 0 1
x
t
=>
Y’
X, X’
0’
0
v
Z
x(t)
x’(t’)
Z’
1 –v
x’
x
2/c2)-½
γ(v)
=
(1
v
=
γ(v)
-v/c2 0 t
t’
1
При v<<c => γ ~= 1, -v/c2 -> 0 преобразования Лоренца
превращаются в преобразования Галилея.
Если время и координаты выражаются друг через друга – это означает
их неразрывную связь. В дальнейшем мы будем использовать термин
пространство-время (space- time)

14.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
Y’
Y
0’ 0
Z
u
X, X’
Y
0
Y’
0’
Z
Z’
x’(t) = x(t) - ut
y’(t) = y(t)
z’(t) - z(t)
t’ = t
r, t = (x, y, z, t) – 4-вектор
(событие)
y’(t) = y(t); z’(t) - z(t),
ограничимся рассмотрением
преобразований 2-вектора (x, t):
u X, X’
x’
t’
γ б
= г д
x
t
Задача: логически найти элементы
матрицы а, б, г, д.

15.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
γ(u) б(u)
= г(u) д(u)
x
t
Задача: логически найти элементы матрицы
γ, б, г, д. Это можно сделать разными
способами. Например
Y’
Y
0’ 0
Z
x’
t’
Шаг 1. Следим из системы К за точкой x’=0.
X, X’ По определению ее координата x = ut, а из
преобразования: 0 = γx + бt = γut + бt =>
u
Y
0
Y’
0’
Z
Z’
б = - γu
Шаг 2. Следим из системы К’ за точкой x=0.
По определению ее координата x’ = -ut’, а
u X, X’ из преобразования: -ut’ = - γut ; t’ = дt =>
д=γ
Шаг 3. γ(u)=γ(-u) – не должно зависеть от
направления скорости

16.

События. Уточняем постановку задачи).
Y
0
Y’
0’
Z’
u
X, X’
Z
γ(u) -uγ(u)
= г(u) γ(u)
x
t
Это вид матрицы после первых трех шагов.
Осталось найти γ(u)= γ (четная функция) и
г(u). Шаг 4: обратное преобразование
Y’
Y
0’ 0
Z
x’
t’
u
X, X’
Y
0
Y’
0’
Z
Z’
x
t
=
γ(u) uγ(u)
г(-u) γ(u)
x'
t'
γ
uγ γ
-uγ
г(-u) γ г(u) γ
u X, X’
=>
1 0
= 0 1
γ2+uγг(u)=1 ; -uγ2 +uγ2 =0
γг(-u)+γг(u)=0 ; γ2- uγг(-u)=1
Вывод: г(и) – функция нечетная

17.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
γ(u) -uγ(u)
= г(u) γ(u)
x
t
Это вид матрицы после первых 4-х шагов.
Шаг 5. Сделаем замену переменной г(u)= Kuγ
(нечетная функция)
Y’
Y
0’ 0
Z
x’
t’
u
X, X’
Y
0
Y’
0’
Z
Z’
1 -u
x'
t' = γ Ku 1
x
t
Учтем (шаг 4), что γ2+uγг(u)=1 => .
u X, X’
=>
γ2+Ku2γ2 =1 => γ = (1 + Ku2)-1/2
остается неясно, что такое K (константа
или, может быть, четная функция от u).
Можно доказать, что константа
(доказательство громоздкое, опускаю…)

18.

Преобразования координат событий.
Y’
0’
Z’
u
Y
0
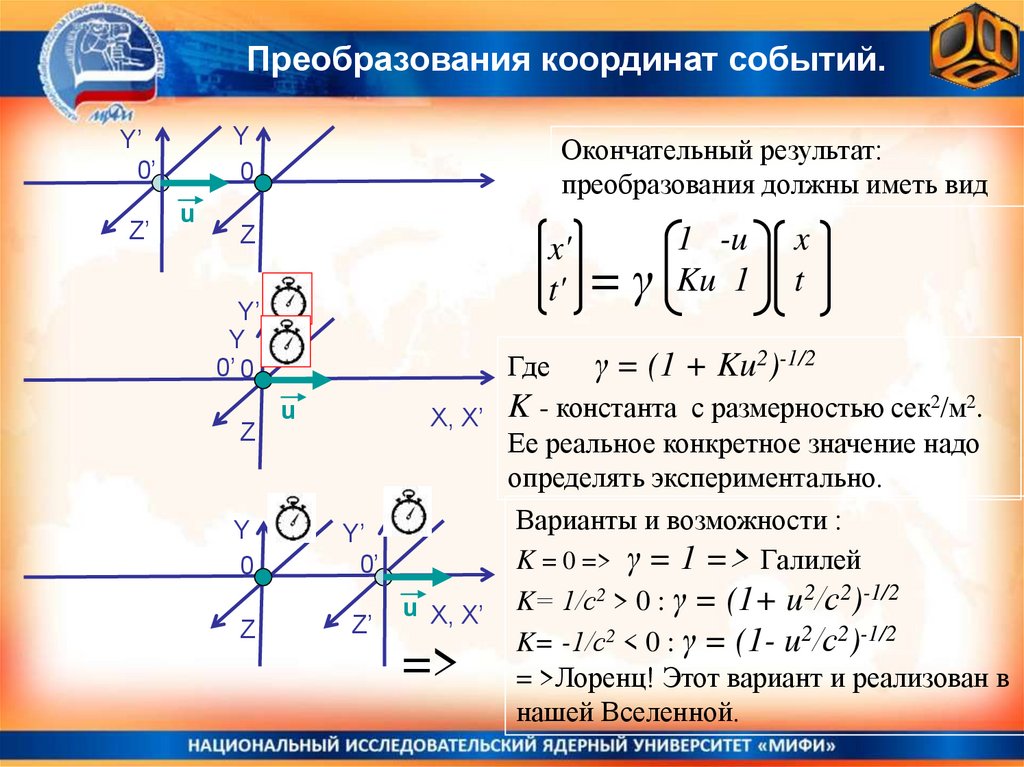
Окончательный результат:
преобразования должны иметь вид
Z
1 -u
x'
t' = γ Ku 1
Y’
Y
0’ 0
Z
Y
0
Z
u
x
t
Где
γ = (1 + Ku2)-1/2
2/м2.
K
константа
с
размерностью
сек
X, X’
Ее реальное конкретное значение надо
определять экспериментально.
Варианты и возможности :
Y’
K = 0 => γ = 1 => Галилей
0’
2 2 -1/2
2
u X, X’ K= 1/с > 0 : γ = (1+ u /с )
Z’
K= -1/с2 < 0 : γ = (1- u2/с2)-1/2
= >Лоренц! Этот вариант и реализован в
нашей Вселенной.
=>

19.

Преобразования Лоренца
x’ = γ (x – ut)
t’ = γ (t - xu/c2)
1
-u
x'
2
t' = γ -u/c 1
γ = (1 - u2/c2 )-1/2
x
t
1
V2
1 2
c
При u << c преобразования Лоренца совпадают с преобразованиями
Галилея. Старая Ньютонова механика была и остается правильной!
При u >c преобразования Лоренца теряют физический смысл => величина с
является предельной скоростью движения и распространения чего-бы то ни
было в природе! Найти конкретное значение с можно экспериментально.
При u < ~ c преобразования Лоренца существенно отличаются от
преобразований Галилея и сильно меняют законы механики. Меняются
правила сложения скоростей, определения импульса и кинетической
энергии.

20.

4-х мерные преобразования Лоренца для механики
В механике при больших
скоростях движения следует
применять преобразования
Лоренца:
Y’
Y’’
Y
X, X’,
0’
0
v
Z
x’ = γ(v) (x - vt)
1
y’ = y
V2
z’ = z
1 2
c
t’ = γ(v)(t - xv/c2)
x’ = γ(v) (x - vt)
t’ = γ(v)(t - xv/c2)
Z’

21.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
1
V2
1 2
c
1. Ход времени в разных системах отсчёта
t’ = γ(v)(t - xv/с 2)
Y
t0= γ(v)(t – v2t/с 2) = t / γ(v)
t = γ(v)t0 > t0 t t0
V2
1 2
c
0
Y’
X=0, Vt, 2Vt, …;
t’ = 0, t0, 2t0…
0’
v
Z
Z’
В движущейся системе отсчета время течет медленнее.
Но какую систему считать движущейся?
x(t)
x’(t’)

22.

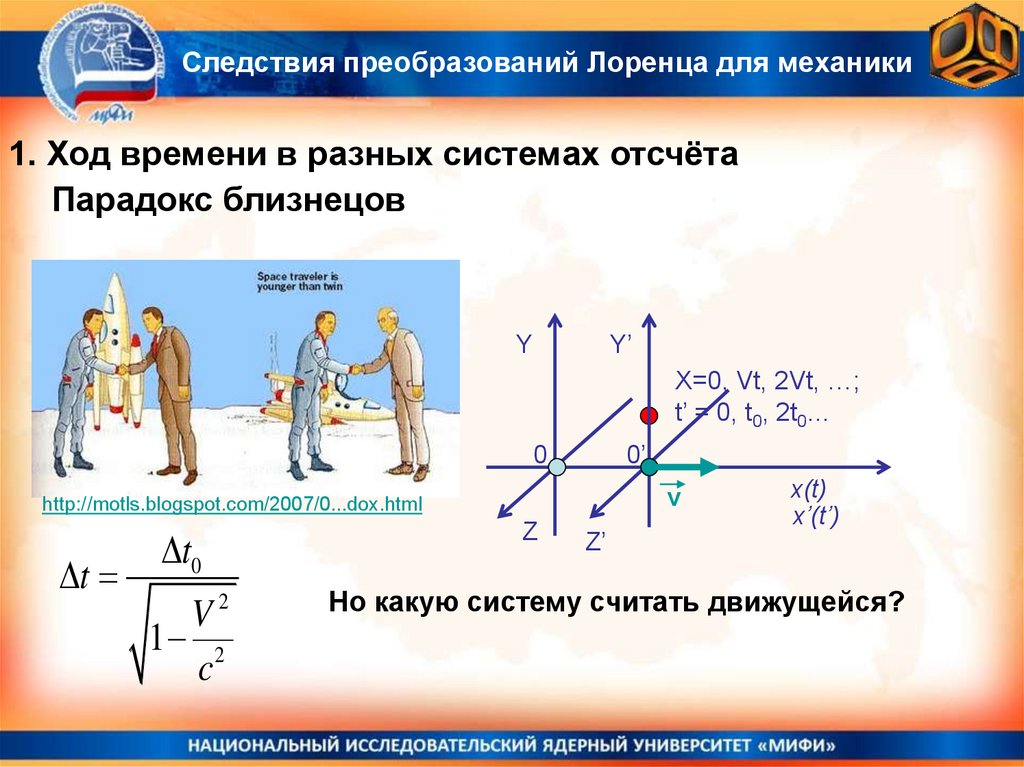
Следствия преобразований Лоренца для механики
1. Ход времени в разных системах отсчёта
Парадокс близнецов
Y’
Y
X=0, Vt, 2Vt, …;
t’ = 0, t0, 2t0…
0
0’
v
http://motls.blogspot.com/2007/0...dox.html
t
t0
V2
1 2
c
Z
Z’
x(t)
x’(t’)
Но какую систему считать движущейся?

23.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
1
V2
1 2
c
2. Неодновременность событий в разных системах
Y’ X= vt, t = t
отсчёта
X=0, t = t Y
t1’ = γ(v)t
X’=0, t2’= ?
X’ = -vt’, t1’= ?
t2’= γ(v)(t – v2t/с2) = t/γ(v)< t1’
0’
0
v
Z
Z’
x(t)
x’(t’)
Если в одной системе отсчета два события кажутся одновременными – в
другой они могут показаться произошедшими в разные моменты времени

24.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
1
V2
1 2
c
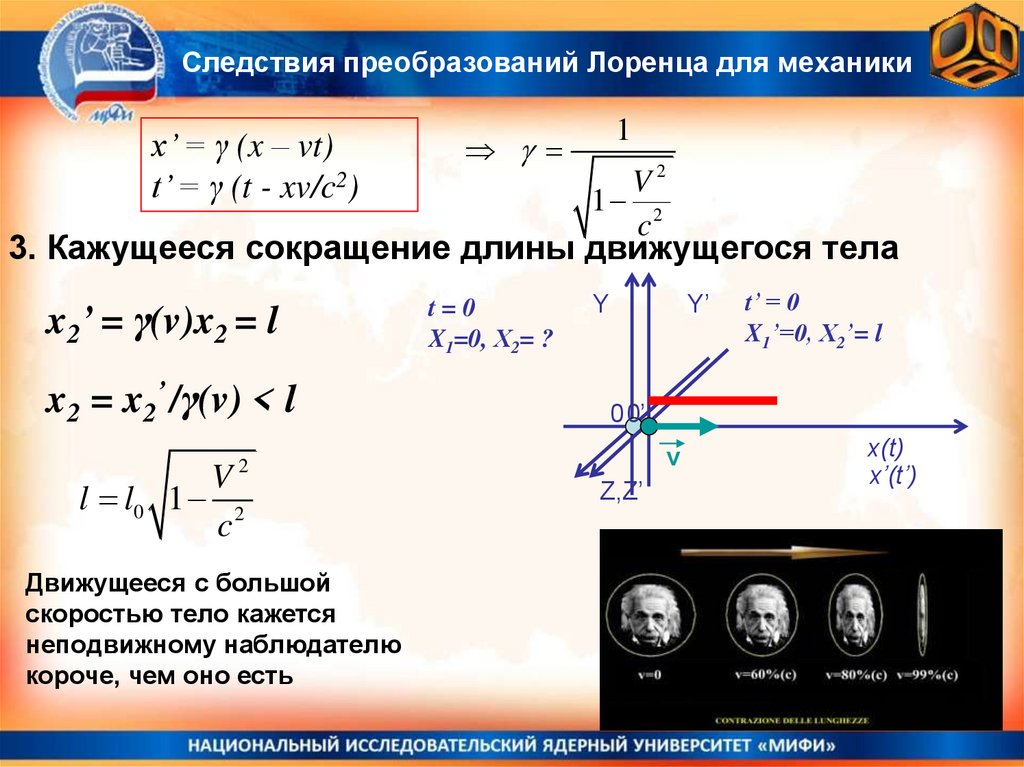
3. Кажущееся сокращение длины движущегося тела
x2’ = γ(v)x2 = l
x2 = x2’ /γ(v) < l
2
V
l l0 1 2
c
Движущееся с большой
скоростью тело кажется
неподвижному наблюдателю
короче, чем оно есть
t=0
X1=0, Х2= ?
Y’
Y
t’ = 0
X1’=0, Х2’= l
0 0’
v
Z,Z’
x(t)
x’(t’)

25.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
Относительная скорость
двух частиц
1
V2
1 2
c
vrel
4. Удивительное сложение скоростей
Y’
Y
Y’’
v3
Y’
Y’’
v1
Y
0’
0
0’’
v1
Z
Z’
v2
0’
0
v2
Z’’
v2 x v1x
,
v1x v2 x
1 2
c
V
Z
Z’
v3 = (v1 + v2)/(1 + v1v2 /с 2) < c
ПРИМЕР: v1 = 0,9c; v2 = 0,9c
cv1 + cv2 < c2 + v1v2
Vrel = (0,9c+0,9c)/(1+0,9 * 0,9)=
=1,8 c/ 1,81 = 0,995c
0 < c2-cv1 –cv2+v1v2 =(c-v1)(c–v2) >0

26.

Преобразования для скоростей
x’ = γ(v) (x - Vt)
y’ = y
z’ = z
t’ = γ(v)(t - xV/c2)
x = γ(v) (x’ + Vt)
y = y’
Y
z = z’
t = γ(v)(t’ + x’/V/c2) 0
γ(v) = (1 - v2/с 2)-1/2
dx dx Vdt
V
dt dt 2 dx
c
dy dy , dz dz
Y’
Y’’
v1
v2
0’
V
Z
dx dy dz
v , , ,
dt dt dt
dx dy dz
v ,
,
dt dt dt
Z’
Относительная скорость
двух частиц
v2 x v1x
vrel
,
v v
1 1 x 22 x
c
2
2
v
1
V
c
v z 1 V 2 c 2
vx V
y
vx
, vy
, vz
,
v xV
v xV
v xV
1 2
1 2
1 2
c
c
c

27.

Инварианты преобразований Лоренца. Интервал.
Точечные события:
P1 x1 , y1 , z1 , t1 , P2 x2 , y2 , z2 , t2
s c t1 t2 r ,
2
12
2
2
2
12
где
r x1 x2 y1 y2 z1 z2
2
12
2
2
Интервал инвариант преобразований Лоренца, т.е.
Y’
Y
t = 0, x=0
t’=0, x’=0
0 0’
v
Z,Z’
2
2
s122 s12
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
x=r, t = t
x’= γ(r-vt)
t’= γ(t-vr/c2)
s12 = c2t2 – r2 = c2γ2(t-vr/c2)2 – γ2(r-vt)2=
= γ2((ct-vr/c)2 –(r-vt)2) =
x(t) = γ2(c2t2-2vrt +v2r2/c2 – r2+2rvt-v2t2) =
x’(t’)
= c2 t 2 – r2

28.

Экспериментальные подтверждения
специальной теории относительности
Эксперимент Хафеле (J.C. Hafele) и Китинга (Richard E. Keating), октябрь 1971
Разность показаний путешествовавших и остававшихся на месте часов, наносекунды
предсказанная
гравитационный вклад
(общая теория относительности)
кинематический вклад
(специальная теория относительности)
измеренная
Всего
на восток
144 ± 14
−184 ± 18
−40 ± 23
−59 ± 10
на запад
179 ± 18
96 ± 10
275 ± 21
273 ± 7

29.

Классические представления
о пространстве и времени
1.
Существует отдельно пространство и независимое от него время.
Пространство является евклидовым, т.е. справедливы аксиомы Евклида.
2.
Существуют инерциальные системы отсчёта, в которых выполняются
второй и третий законы Ньютона.
3.
Справедлив принцип относительности Галилея, который гласит, что во всех
инерциальных системах отсчёта одинаковы все законы механики, а также
свойства пространства и времени.
4.
Справедливы преобразования Галилея координат и времени и абсолютный
характер одновременности событий. Выполняется классический закон
сложения скоростей.

30.

Новые (релятивистские) представления
о пространстве и времени
1. Пространство и время являются двумя проявлениями единой сущности –
пространства-времени. Геометрия пространства-времени не является Евклидовой и
подлежит экспериментальному и теоретическому исследованию.
2. Существуют инерциальные системы отсчёта, в которых, если на тело не действуют
реальные физические силы – оно движется равномерно и прямолинейно.
3. Справедлив принцип относительности Галилея, который гласит, что во всех
инерциальных системах отсчёта одинаковы все законы механики, а также свойства
пространства и времени.
4.
Справедливы
преобразования
Лоренца
для
координат
инвариантом преобразований Лоренца является интервал
и
времени,
причем

31.

Постулаты СТО
Постулаты механики:
1.Все законы природы во
всех ИСО одинаковы
(И. Ньютон).
2) Экспериментальный
факт: существует
максимально возможная
скорость распространения
взаимодействий (скорость
света в вакууме), которая
одинакова во всех
направлениях и не зависит
от скоростей источника и
приемника
(А. Эйнштейн)
Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light
Alexander POPE (1688-1744)
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.
(С. Маршак)
It did not last; the devil, howling
"Ho! Let Einstein be!" restored the status quo.
John Squire (1884 -1958)
Но очень скоро чёрт пролаял «Нет!.
Явись. Эйнштейн!» – и снова гаснет
свет…

32.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Thank you for attention!
İlginiz için teşekkür ederiz!
আপনার মননান ানগর জনয আপনানে
ধনযিাদ!
Cảm ơn bạn đã quan tâm của bạn!
Gracias por su atención!
Dziękuję za uwagę!

33.

Пример матричного умножения векторов:
Преобразование координат при повороте СК:
x’ = x cos φ – y sin φ
y’ = x sin φ + y cos φ
x’
y’
cos φ –sin φ
= sin φ cos φ
y’
y
φ
x
0
x
y
x’
x’ = x cos φ – y sin φ + 0*z
y’ = x sin φ + y cos φ + 0*z
z’ = 0*x + 0*y
+z
x’
y’
z'
cos φ –sin φ 0
= sin φ cos φ 0
0
0
1
x
y
z
=>
Mx
Ixx Ixy Ixz
My = Iyx Iyy Iyz
Mz
Izx Izy Izz
ωx
ωy
ωz