Similar presentations:
Элементы релятивистской механики
1. Курс общей физики
КУРСОБЩЕЙ
ФИЗИКИ
ЛЕКЦИЯ 4
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ
2. ПОСТУЛАТЫ СТО
СТО основывается на следующих положениях:1. принцип относительности Эйнштейна: все законы
природы инвариантны при переходе от одной
инерциальной системы отсчета к другой.
2. принцип независимости скорости света в
инерциальных системах отсчета от скорости движения
источника и приемника (скорость света не может
превышать ~3∙108 м/с).
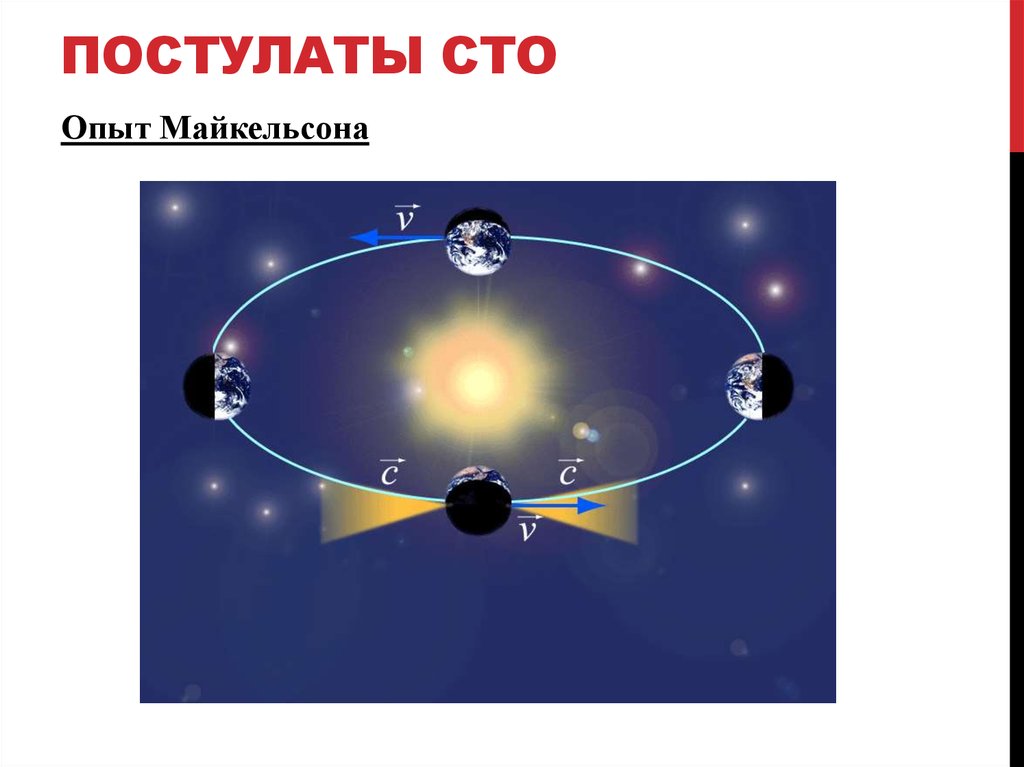
3. ПОСТУЛАТЫ СТО
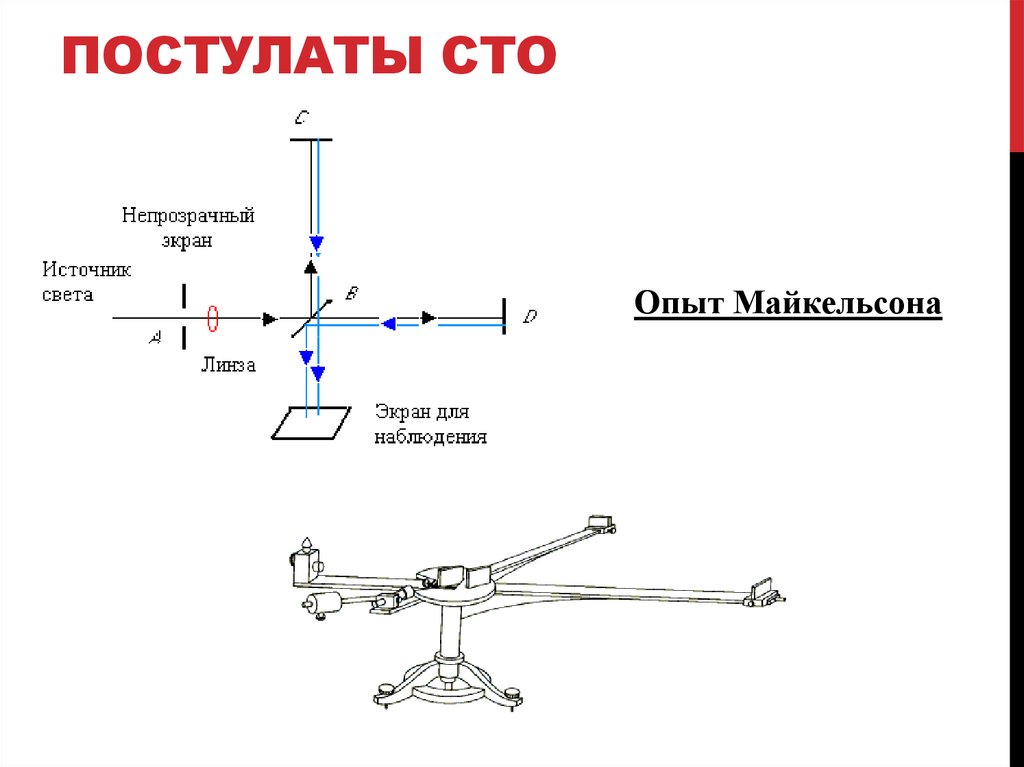
Опыт Майкельсона4. ПОСТУЛАТЫ СТО
Опыт Майкельсона5. Преобразования лоренца
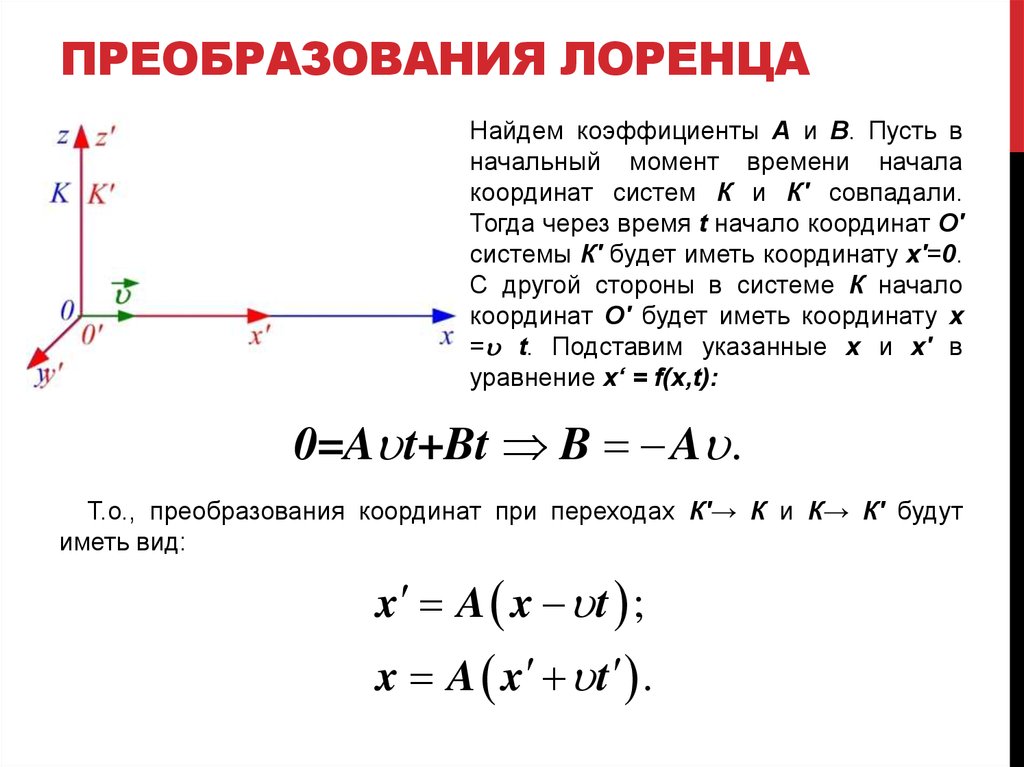
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦАРассмотрим инерциальные системы
отсчета K и K‘. Направим оси координат
этих систем отсчета как на рисунке.
Система К' движется со скоростью u
относительно
системы
К.
Пусть
происходит
некоторое
событие,
которому в системе К соответствуют
координаты x, y, z и время t, а в
системе К' - x', y', z' и время t'. Найдем
преобразования координат и времени
при переходе из одной инерциальной
системы отсчета в другую.
Так как системы координат К и К' равноправны, то преобразования
координат и времени должны быть такими, чтобы их можно было обращать
при переходе от преобразования К→К' к преобразованию К'→ К.
В связи с этим данные преобразования должны быть линейными
функциями. Значит функцию x‘ = f(x,t) можно представить в виде
x =Ax+Bt.
6. Преобразования лоренца
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦАНайдем коэффициенты А и B. Пусть в
начальный момент времени начала
координат систем К и К' совпадали.
Тогда через время t начало координат O'
системы К' будет иметь координату x'=0.
С другой стороны в системе К начало
координат O' будет иметь координату x
=u t. Подставим указанные x и x' в
уравнение x‘ = f(x,t):
0=Au t+Bt B Au .
Т.о., преобразования координат при переходах К'→ К и К→ К' будут
иметь вид:
x A x u t ;
x A x u t .
7. Преобразования лоренца
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦАДля нахождения коэффициента A снова
рассмотрим
начальный
момент
времени, когда начала координат О и О'
совпадали. Представим, что в данный
момент времени из начала координат
начинает
распространяться
свет.
Расстояния, которые свет пройдет в
системах отсчета К и К', будут равны
x x c t и x x c t ,
Подставим последние значения x и x' в преобразования x'→x и x→x'.
Получим
ct At c u ;
ct At c u .
8. Преобразования лоренца
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦАРешив данную систему относительно А
придём к
A
1
1 u c
2
.
Окончательно выражения для преобразований координат будут иметь вид
x
x ut
1 u c
2
; x
x u t
1 u c
2
.
9. Преобразования лоренца
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦАДалее найдем преобразование времени
для систем координат К и К'. Для этого
в
полученные
преобразования
координат подставим t и t' из выражений
x c t и x c t ,
t
t
ux
c
2
1 u c
2
; t
t
откуда
u x
c2
1 u c
2
.
Полученные преобразования координат и времени называются
преобразованиями Лоренца. В отличие от преобразований Галилея,
данные преобразования справедливы также и для движения тел со
скоростями, близкими к с скорости света.
10. Релятивистский закон сложения скоростей
РЕЛЯТИВИСТСКИЙ ЗАКОНСЛОЖЕНИЯ СКОРОСТЕЙ
Согласно преобразованиям Галилея
скорость тела U в системе K связана со
скоростью тела U' в системе K'
соотношением
U U u.
Данное преобразование противоречит положению СТО о независимости
скорости света от скорости источника и приемника света. Получим
релятивистский закон сложения скоростей.
Пусть в течении промежутка времени от t1 до t2 координаты тела
изменились от x1 до x2 в системе отсчета К . Тогда можно записать. что
t = t 2 t 1
t
u x
c2
1 u c
2
, x x2 x1
x u t
1 u c
2
.
11. Релятивистский закон сложения скоростей
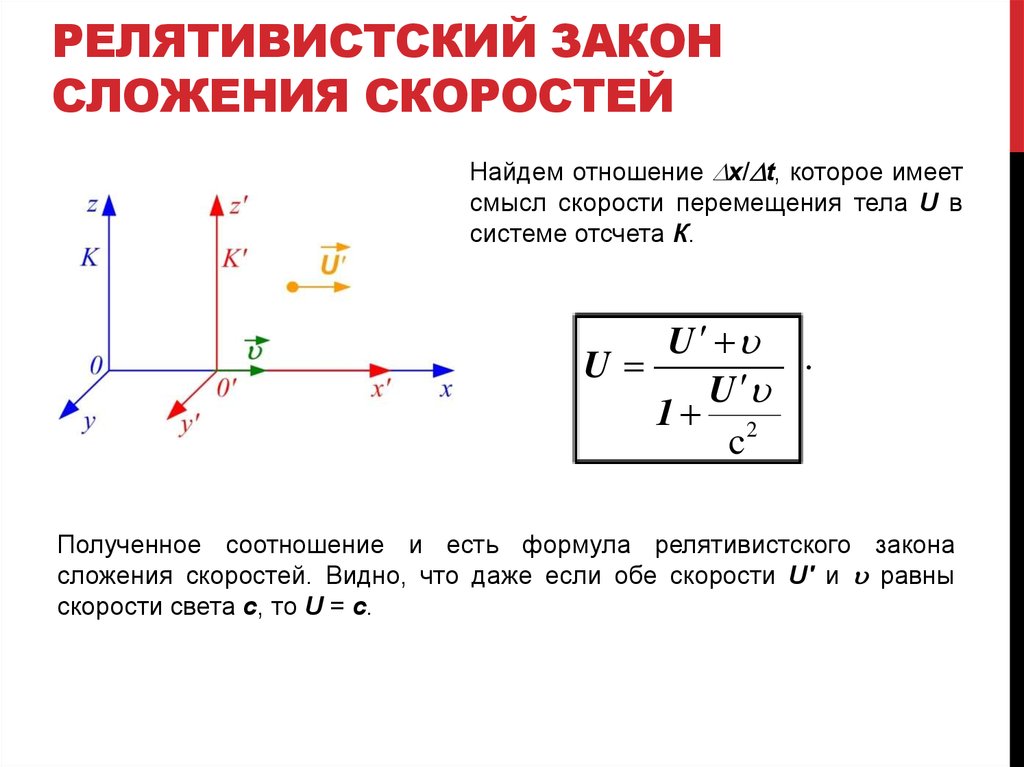
РЕЛЯТИВИСТСКИЙ ЗАКОНСЛОЖЕНИЯ СКОРОСТЕЙ
Найдем отношение x/ t, которое имеет
смысл скорости перемещения тела U в
системе отсчета К.
U u
U
U u
1 2
c
Полученное соотношение и есть формула релятивистского закона
сложения скоростей. Видно, что даже если обе скорости U' и u равны
скорости света c, то U = c.
12. Следствия преобразований лоренца
СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙЛОРЕНЦА
Относительность одновременности событий
Пусть
в
системе
К
происходят
последовательно два события. Этим
событиям
соответствуют
моменты
времени t1 и t2 и координаты x1 и x2
(координаты y и z совпадают). Если t1 = t2
(события происходят одновременно), то t
= 0. Найдем промежуток времени между
данными событиями в системе отсчета K':
t
x1 x 2
u
c 2 0.
1 u c
2
Т.о., оказывается, что одновременные события в одной инерциальной
системе отсчета не всегда одновременны в другой инерциальной системе
отсчета.
13. Следствия преобразований лоренца
СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙЛОРЕНЦА
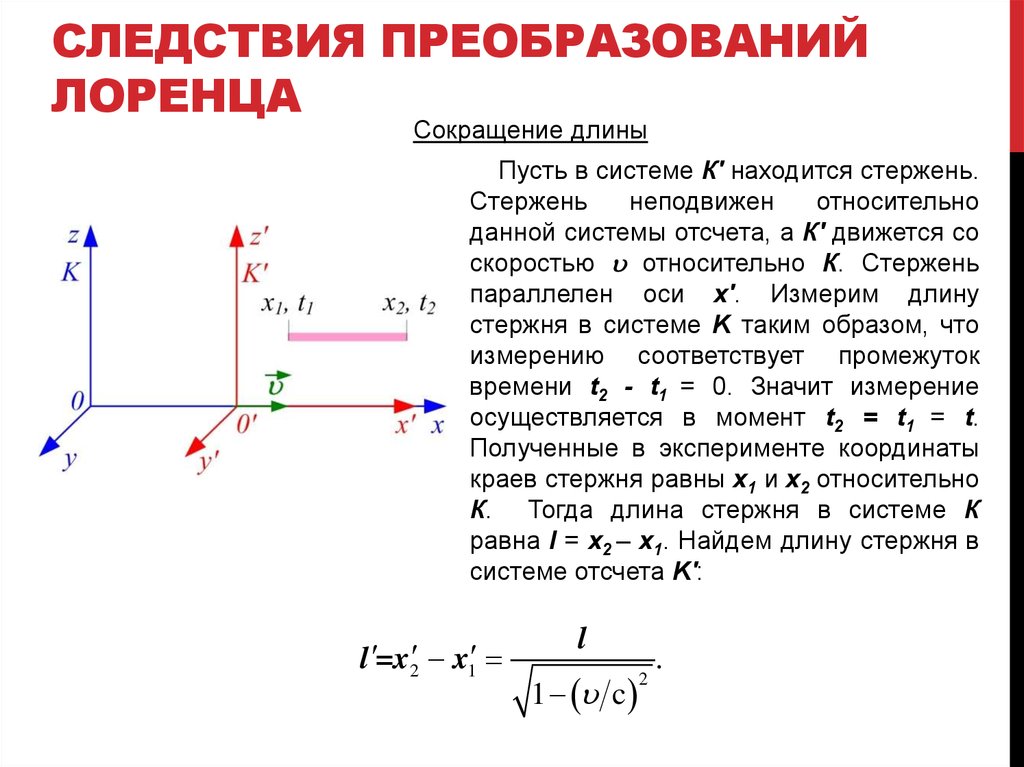
Сокращение длины
Пусть в системе К' находится стержень.
Стержень
неподвижен
относительно
данной системы отсчета, а К' движется со
скоростью u относительно К. Стержень
параллелен оси х'. Измерим длину
стержня в системе K таким образом, что
измерению соответствует промежуток
времени t2 - t1 = 0. Значит измерение
осуществляется в момент t2 = t1 = t.
Полученные в эксперименте координаты
краев стержня равны x1 и x2 относительно
К. Тогда длина стержня в системе К
равна l = x2 – x1. Найдем длину стержня в
системе отсчета K':
l =x2 x1
l
1 u c
2
.
14. Следствия преобразований лоренца
СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙЛОРЕНЦА
Сокращение длины
Учитывая, что длина стержня в
системе отсчета, относительно которой он
покоится, называется собственной и
обозначается l0, последнее выражение
записывается в виде
l=l0 1 u c .
2
Т.о., размеры тела в направлении движения сокращаются. В то
же время поперечные размеры (перпендикулярно направлению
движения) остаются неизменными.
15. Следствия преобразований лоренца
СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙЛОРЕНЦА
Длительность события
Пусть в системе К' в точке x'
происходит некоторое событие. Событию
соответствует интервал времени t'= t2' t1'. Найдем длительность события в
системе отсчета K:
t
t = t 2 t 1
.
2
1 u c
Интервал времени t' называется собственным временем события
(измерено в той системе отсчета, в которой событие происходит). Как
правило данное время обозначают t0. С учетом этого длительность
события t в системе К рассчитывается по формуле:
t =
t0
1 u c
2
.
Т.о., длительность события минимальна в той системе отсчета, в
которой событие происходит. И сокращение размеров тела и увеличение
длительности события есть кинематические эффекты, являются
проявлениями фундаментальных свойств пространства и времени.
16. Элементы релятивистской динамики
ЭЛЕМЕНТЫДИНАМИКИ
РЕЛЯТИВИСТСКОЙ
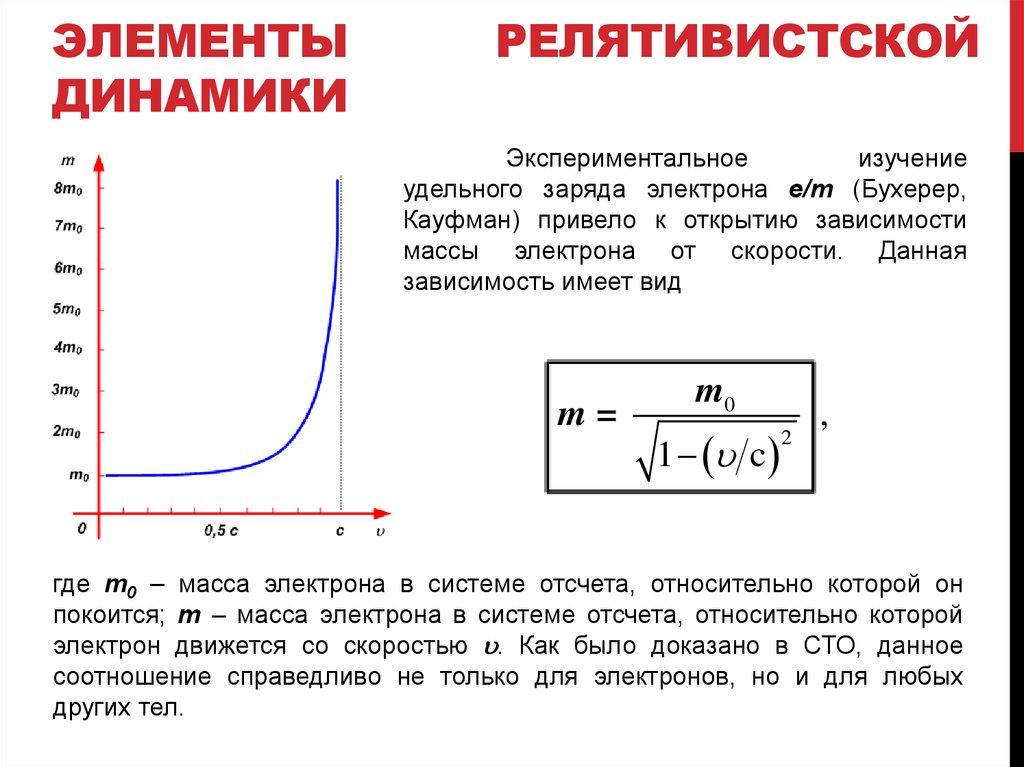
Экспериментальное
изучение
удельного заряда электрона e/m (Бухерер,
Кауфман) привело к открытию зависимости
массы электрона от скорости. Данная
зависимость имеет вид
m=
m0
1 u c
2
,
где m0 – масса электрона в системе отсчета, относительно которой он
покоится; m – масса электрона в системе отсчета, относительно которой
электрон движется со скоростью u. Как было доказано в СТО, данное
соотношение справедливо не только для электронов, но и для любых
других тел.
17. Элементы релятивистской динамики
ЭЛЕМЕНТЫДИНАМИКИ
РЕЛЯТИВИСТСКОЙ
Учитывая зависимость массы тела от скорости, релятивистский импульс
тела равен
p=mu =
m0 u
1 u c
2
.
Отсюда можно получить основное уравнение релятивистской динамики
d m0 u
F
dt 1 u c 2
.
18. Энергия в релятивистской механике
ЭНЕРГИЯМЕХАНИКЕ
В
РЕЛЯТИВИСТСКОЙ
Используем основное уравнение релятивистской динамики для
получения релятивистского выражения энергии тела. Умножим данное
выражение на u dt:
d m0 u
F u dt
dt 1 u c 2
u dt .
Выражение F u dt
равно dA - элементарной работе, совершаемой на
телом за время dt. Как известно, работа совершаемая над телом равна
приращению энергии тела:
dA dE .
Значит
m0 u
dE u d
1 u c 2
.
19. Энергия в релятивистской механике
ЭНЕРГИЯМЕХАНИКЕ
В
РЕЛЯТИВИСТСКОЙ
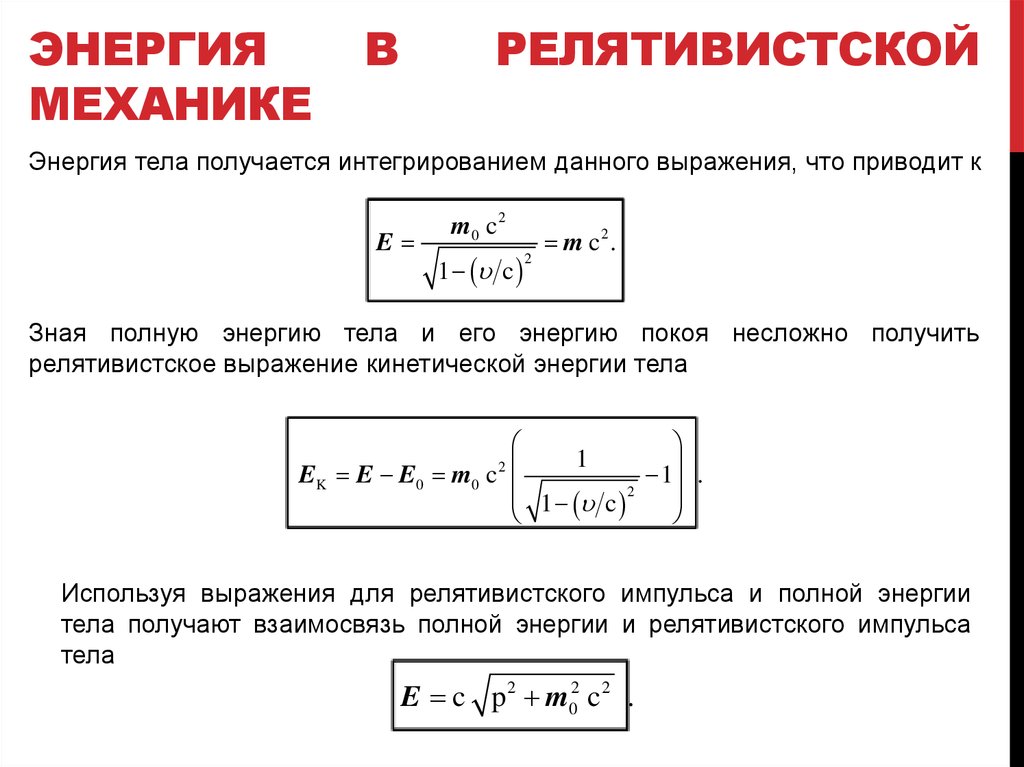
Энергия тела получается интегрированием данного выражения, что приводит к
E
m0 c 2
1 u c
2
m c2 .
Зная полную энергию тела и его энергию покоя несложно получить
релятивистское выражение кинетической энергии тела
1
E K E E 0 m0 c
1 .
1 u c 2
2
Используя выражения для релятивистского импульса и полной энергии
тела получают взаимосвязь полной энергии и релятивистского импульса
тела
E c p 2 m02 c 2 .












 physics
physics








