Similar presentations:
Задачи с параметром и методы их решения
1.
Задачи с параметром и методы ихрешения.
учитель математики
МАОУ «Лицей №37»
Г. Саратова
Летучева Марина
Анатольевна
2.
Методы решения задач с параметромАлгебраический метод
Функциональный метод
Функционально-графический метод
Геометрический метод
Комбинированный метод
3.
Алгебраический метод4.
5.
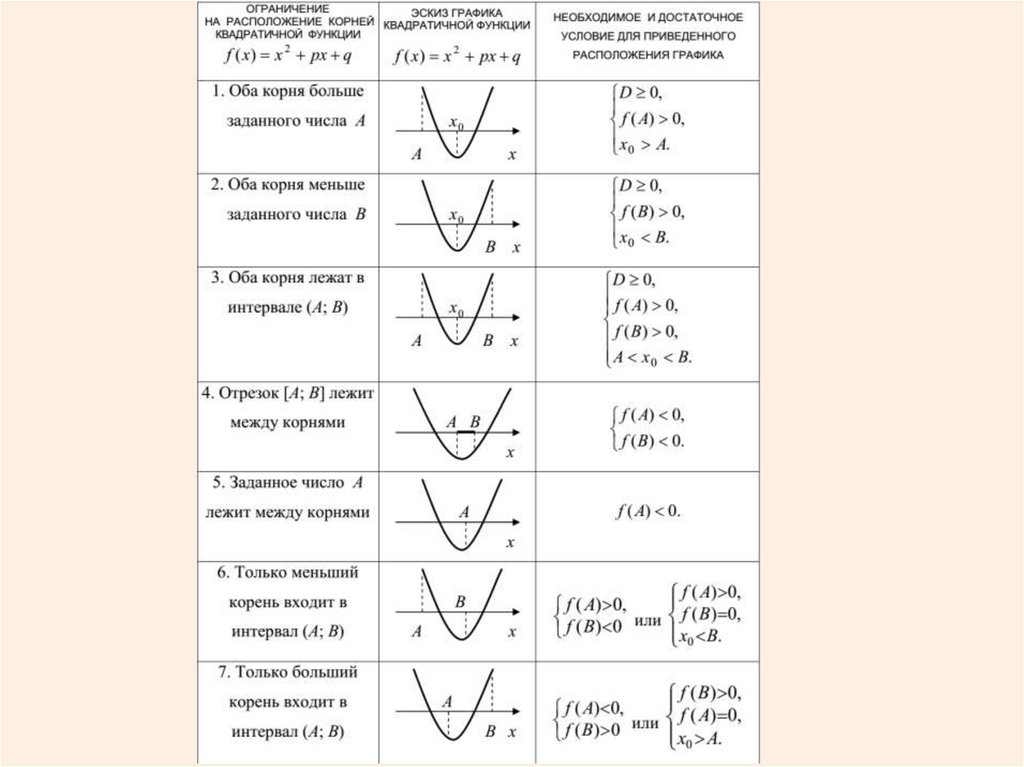
Задачи, сводящиеся к исследованиюквадратного трёхчлена
ПРИМЕР 2.Найдите все значения параметра а, при которых
уравнение
имеет ровно два различных корня.
Решение.
Исходное уравнение имеет два различных корня , если
уравнение
Имеет ровно один корень больше 1.
6.
1)7.
2) Уравнениеимеет два корня, один из
которых больше 1, а другой меньше 1, тогда и только тогда,
когда выполняется условие
т.е.
8.
Задачи, сводящиеся к исследованиюквадратного трёхчлена
ПРИМЕР 5.Найдите все значения параметра а, при которых
уравнение
имеет хотя бы одно решение.
Решение.
9.
Задачи, сводящиеся к исследованиюквадратного трёхчлена
10.
11.
Задачи, сводящиеся к исследованиюквадратного трёхчлена
12.
Функциональный метод13.
14.
Использование ограниченности функции.Метод оценки (минимаксные задачи)
15.
Использование ограниченности функции.Метод оценки (минимаксные задачи)
ЕГЭ 2013. Найдите все значения а, при каждом из которых
уравнение
имеет хотя бы один корень.
Решение.
Рассмотрим две функции
Поскольку
получаем
Функция
является кусочно-линейной, при
угловой коэффициент равен либо 3, либо 9, а при
угловой коэффициент равен либо -3, либо – 9. Значит функция
возрастает при
и убывает при
,
Поэтому
16.
Использование ограниченности функции.Метод оценки (минимаксные задачи)
Исходное уравнение имеет один корень тогда и только тогда,
когда
т.е.
Значит, 1)
2)
17.
Чётность нечётность функции.18.
При каких значениях а система имеетединственное решение? Найдите это
решение.
19.
Монотонность функцииЕГЭ 2014. Найти все значения параметра а, при которых
уравнение
имеет хотя бы
одно решение.
Решение.
Запишем уравнение в виде:
Рассмотрим функцию
Она возрастает на всей области
определения. Исходное уравнение имеет решение тогда и только
тогда, когда
следовательно
Функция
монотонно
возрастает на отрезке
и принимает на нем значения от 4
до 2. Значит уравнение
а с ним и исходное
уравнения имеют решение при
20.
Монотонность функции21.
При каких значениях а уравнение не имеетдействительных решений?
22.
Функционально- графический метод23.
Функционально- графический метод24.
Функционально- графический метод25.
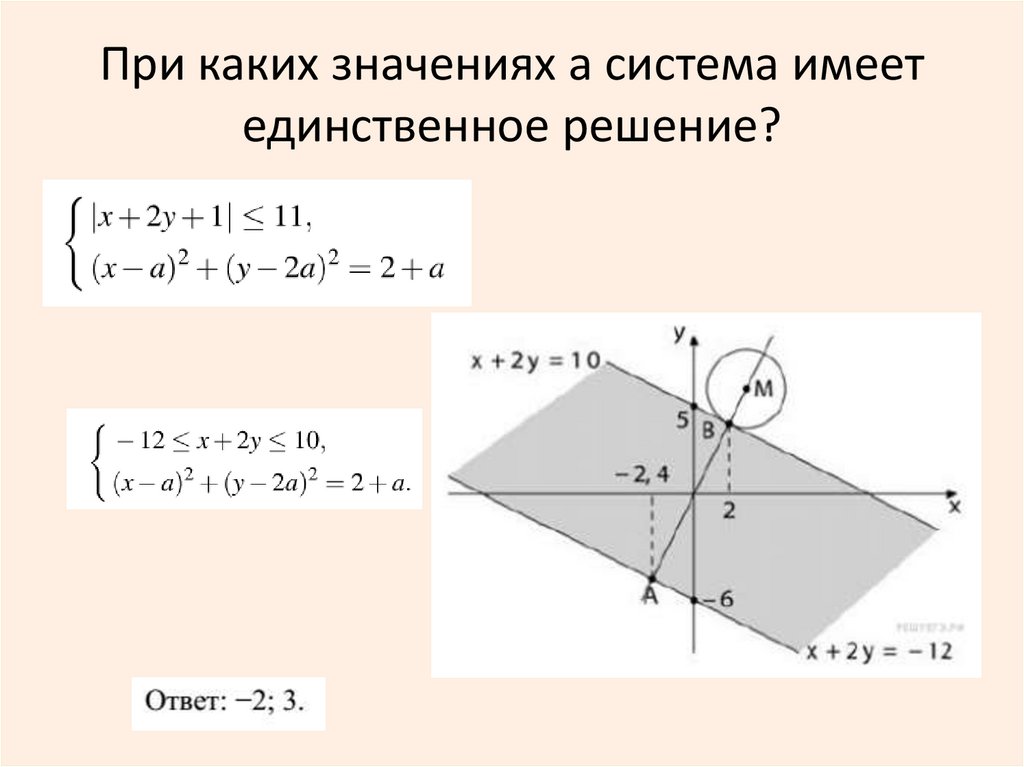
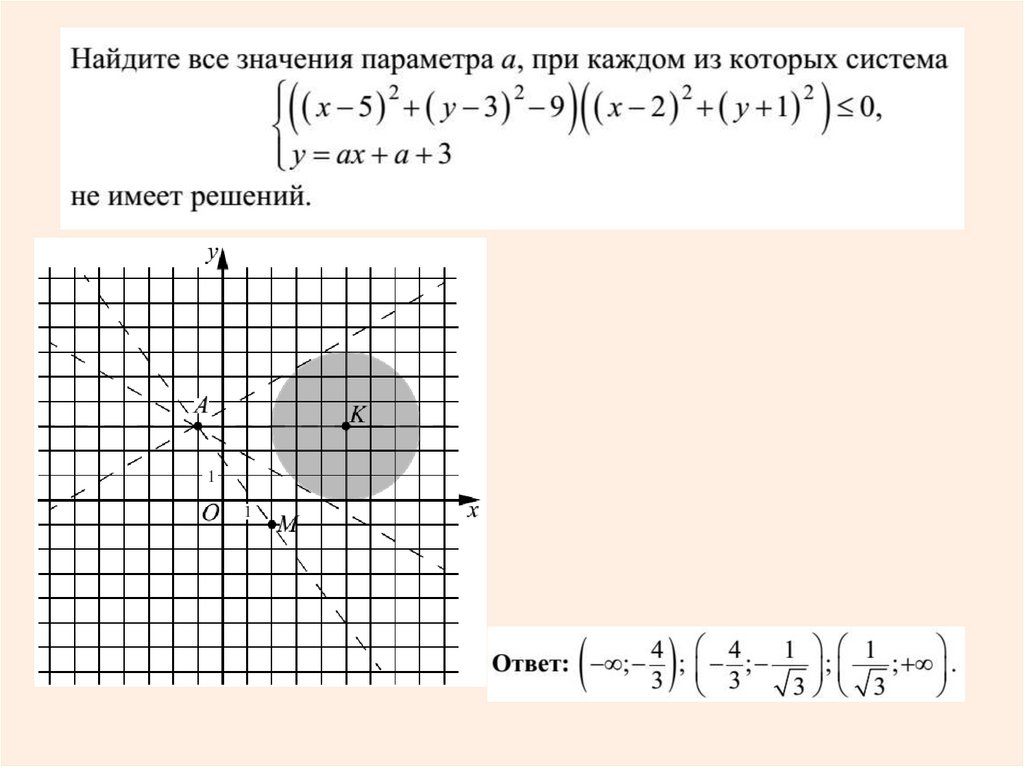
При каких значениях а система имеетединственное решение?
























 mathematics
mathematics








