Similar presentations:
Решение систем линейных алгебраических уравнений (СЛАУ)
1.
Решение систем линейных алгебраическихуравнений (СЛАУ)
1.
Постановка задачи
2.
Методы решения:
метод Гаусса
метод ортогонализации
метод простой итерации (МПИ),
метод Зейделя, метод Монте-Карло,
итерационная
схема
метода
ортогонализации.
2.
Постановка задачиВиды методов:
1. прямые (точные)
конечное число арифметических операций
метод Гаусса, метод Крамера, матричный метод,
метод ортогонализации.
2. итерационные (приближённые)
решение
передел
последовательных
приближений, вычисляемых по единой схеме
метод простой итерации (МПИ), метод Зейделя,
метод Монте-Карло, итерационная схема метода
ортогонализации.
3.
a11x1 a12 x2 ... a1n xn a1n 1 ;a x a x ... a x a ;
21 1 22 2
2n n
2 n 1
...
am1 x1 am 2 x2 ... amn xn amn 1.
(*)
4.
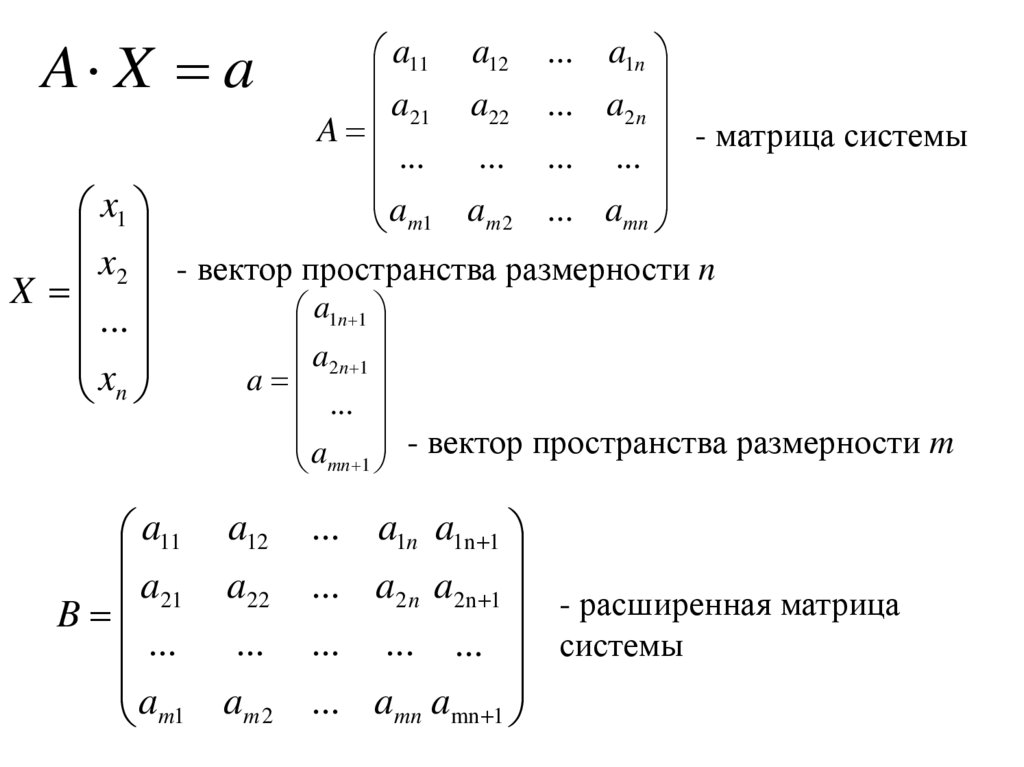
A X a... a1n
... a2 n
- матрица системы
... ...
x1
... amn
x2 - вектор пространства размерности n
X
...
x
n
a11 a12
a21 a22
A
...
...
a
m1 am 2
a1n 1
a2 n 1
a
...
a - вектор пространства размерности m
mn 1
a11 a12
a21 a22
B
...
...
a
m1 am 2
... a1n a1n 1
... a2 n a2n 1 - расширенная матрица
... ... ... системы
... amn amn 1
5.
Матричный метод1
A X a / A слева
1
1
A A X A a
E
1
E X A a
1
X A a
6.
Решение системы (*)- упорядоченная совокупность чисел
c1 , c2 , ..., cn
Равносильные системы уравнений
- решения одной являются решениями другой и
наоборот.
7.
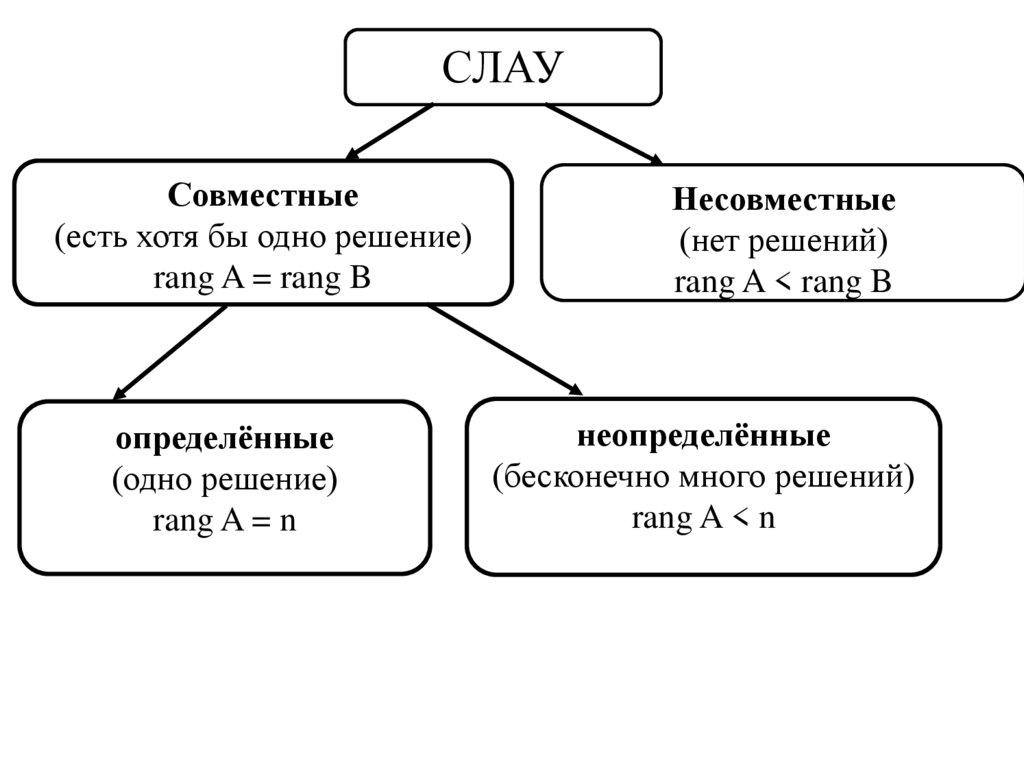
СЛАУСовместные
(есть хотя бы одно решение)
rang A = rang B
определённые
(одно решение)
rang A = n
Несовместные
(нет решений)
rang A < rang B
неопределённые
(бесконечно много решений)
rang A < n
8.
a11 x1 a12 x 2 ... a1n x n a1n 1 ;a x a x ... a x a ;
21 1
22 2
2n n
2 n 1
(1)
...
a n1 x1 a n 2 x 2 ... a nn x n a nn 1 .
9.
Квадратная матрица A невырожденная если |A|≠0Теорема. СЛАУ с n неизвестными, имеющая
невырожденную матрицу, совместна и имеет
единственное решение (т.е. является определённой).
A
T
транспонированная матрица
A AT Симметрическая матрица a ij a ji
A A E
T
A
1
Ортогональная матрица
обратная матрица
A A
1
1
A A E
10.
Метод Гауссаэтапы
прямой ход –
последовательное исключение неизвестных;
обратный
ход
–
последовательное
нахождение неизвестных, начиная с xn
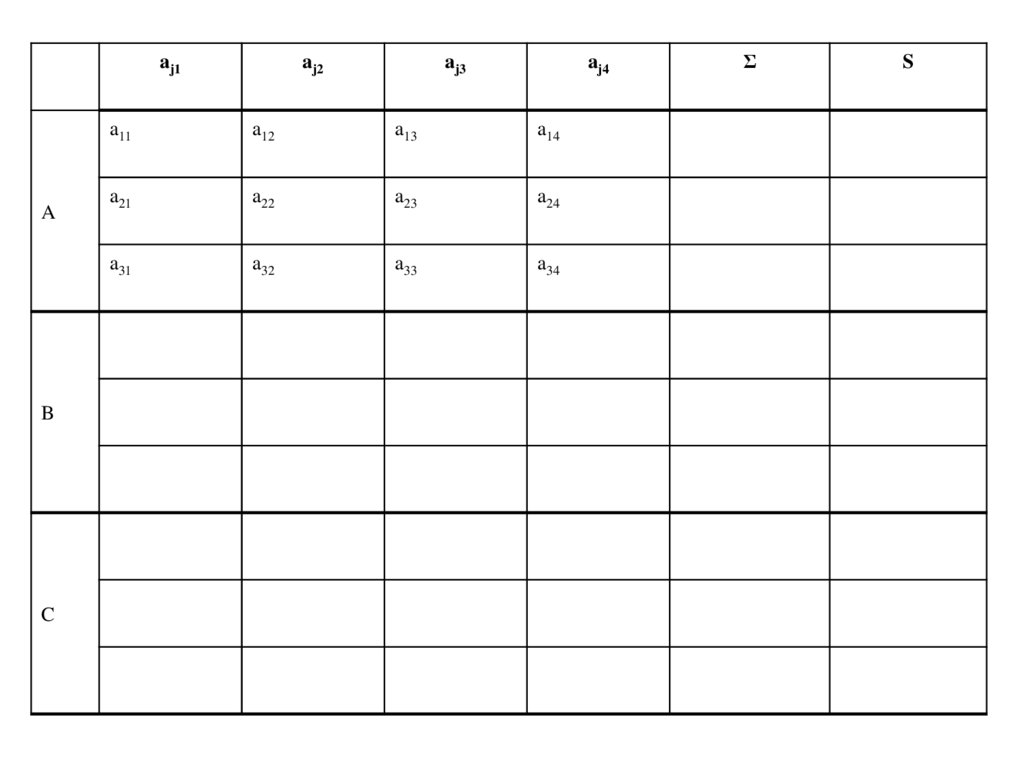
11.
aj1A
B
C
aj2
aj3
aj4
a11
a12
a13
a14
a21
a22
a23
a24
a31
a32
a33
a34
Σ
S


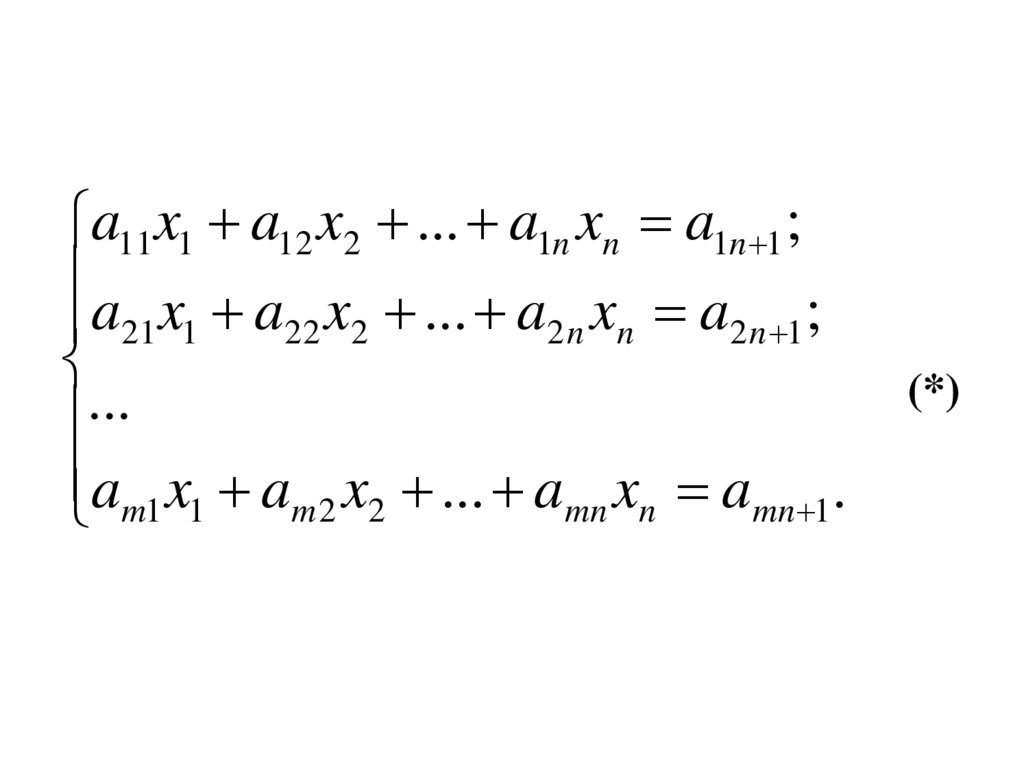
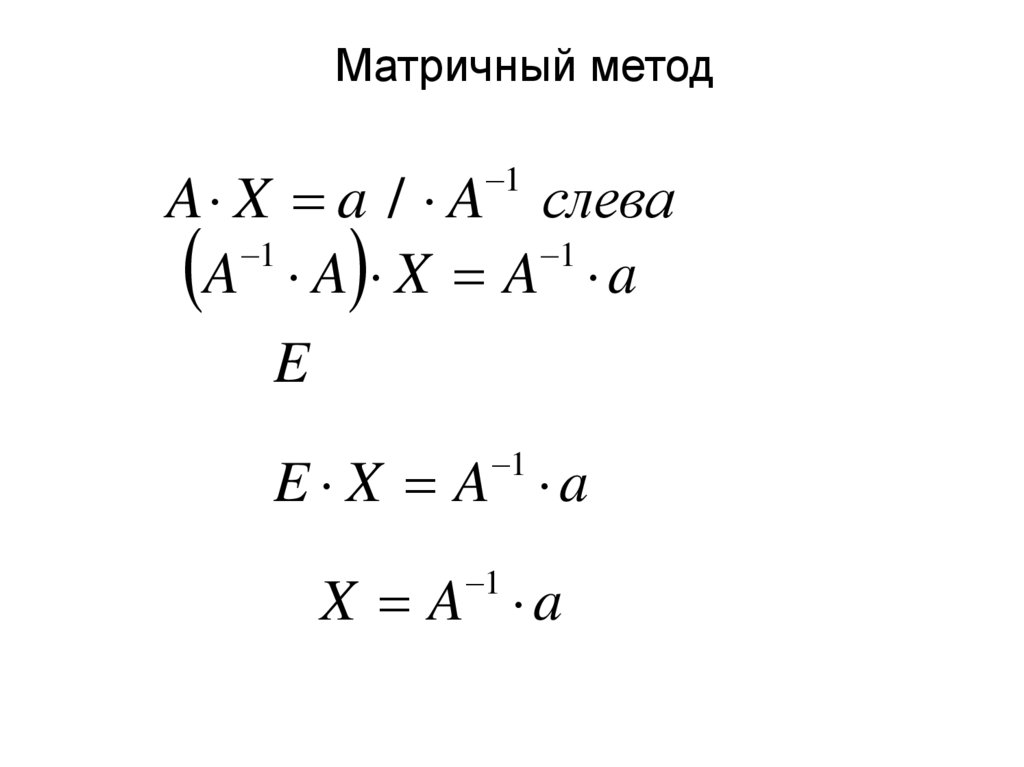

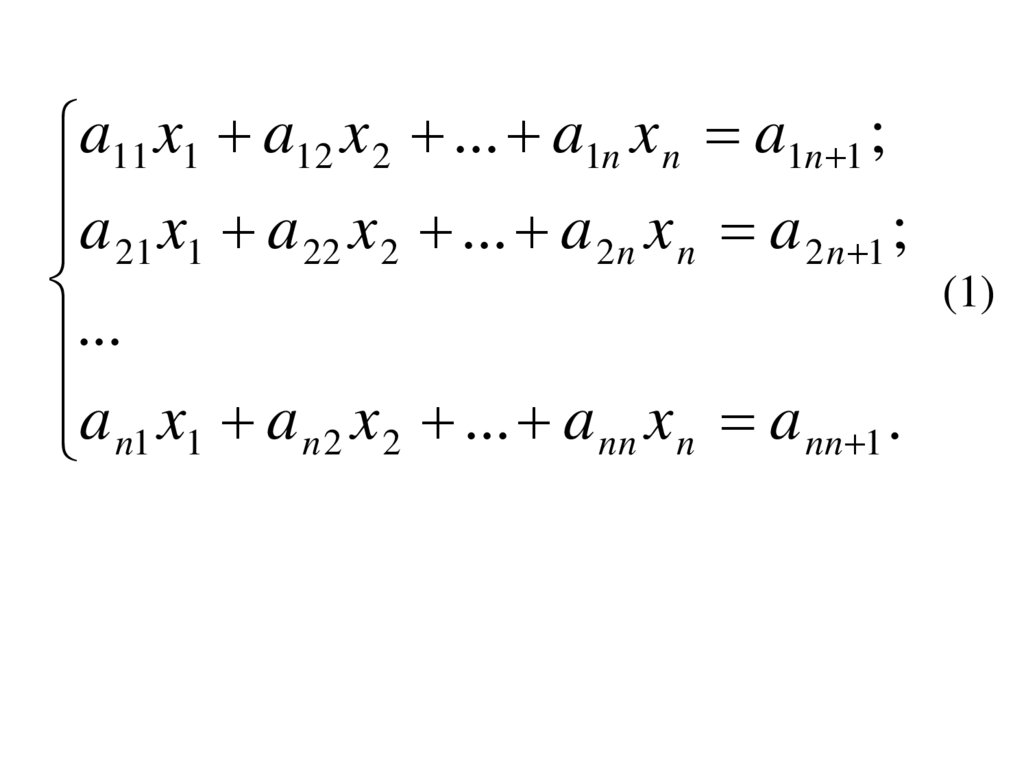


 mathematics
mathematics








