Similar presentations:
Понятие первообразной
1.
2.
Цели урока:-Сформировать
представление
о
понятии
"первообразная", способствовать формированию умений
применять полученные знания в новой ситуации.
Установить связь между производной и первообразной,
формировать умение проверять является ли данная
функция первообразной для другой, заданной на
некотором числовом промежутке функции.
-развивать навыки мыслительной деятельности при
анализе и структурировании учебного материала
-Способствовать привитию культуры умственного труда,
воспитывать организованность и сосредоточенность
3.
Устная работа1
сosх
sinх+12
4.
Устная работа5.
Используя определение производной функции,решают ряд задач в алгебре, физике, химии.
Рассмотрим физический смысл производной.
материальная
точка
s(t) закон
движения
6.
Задача:Точка движется прямолинейно по закону
s(t) = t3+ 2t ( где s(t) – измеряется в м).
Найдите скорость точки в момент времени t=2с.
Решение:
v(t) = 3t2 + 2
v(2) =
Ответ: 14 м/с.
7.
Что мы сделали за урок?Повторили определение производной функции и
формулы дифференцирования.
Решили задачу на применение производной:
зная закон движения, нашли скорость при
заданном времени.
В математике часто приходиться решать
обратную задачу:
зная скорость найти закон движения.
8.
Задача: По прямой движется материальная точка,скорость которой в момент времени t задается
формулой v(t) = 3t2. Найдите закон движения.
Решение: Пусть s(t) – закон движения
надо найти функцию,
производная которой
равна 3t2 .
Эта задача решена верно, но не полно.
Эта задача имеет бесконечное множество решений.
3t2
3t2
3t2
3t2
можно сделать вывод, что
любая функция вида
s(t)=t3+C является
решением данной задачи,
где C любое число.
9.
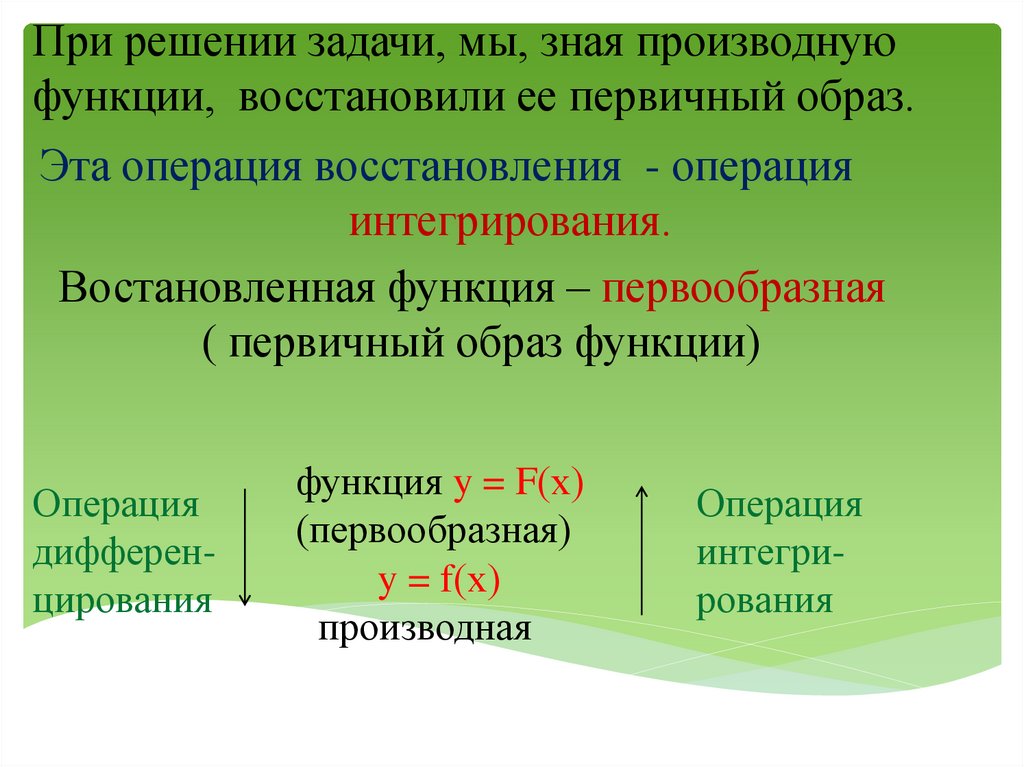
При решении задачи, мы, зная производнуюфункции, восстановили ее первичный образ.
Эта операция восстановления - операция
интегрирования.
Востановленная функция – первообразная
( первичный образ функции)
Операция
дифференцирования
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
10.
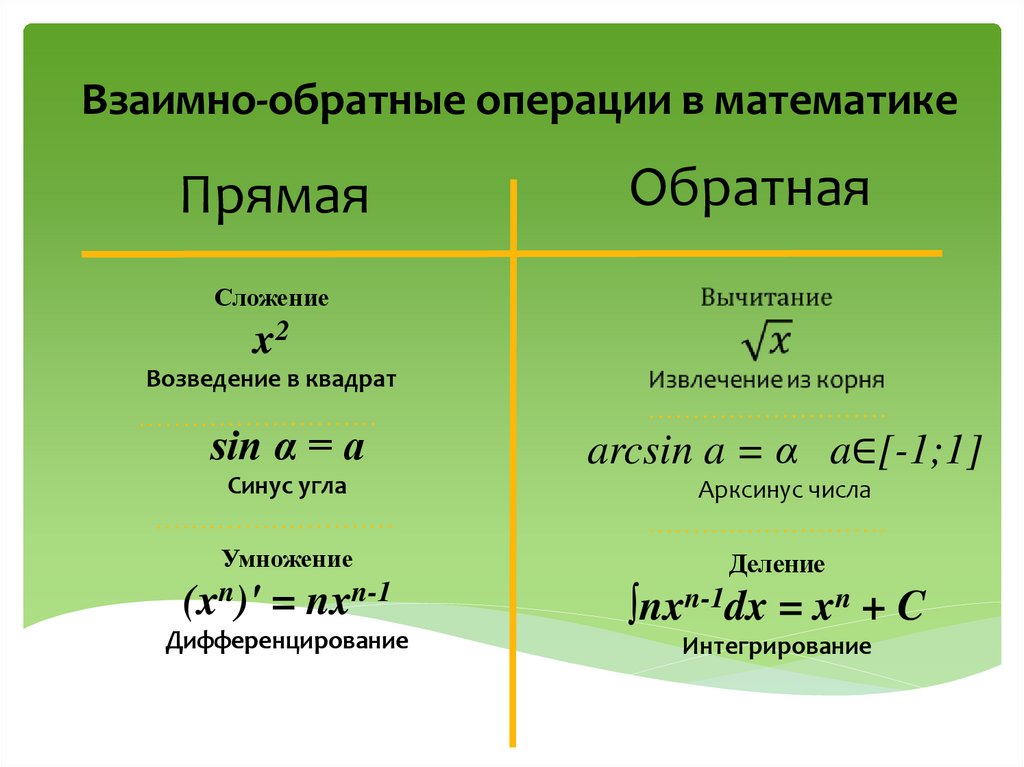
Взаимно-обратные операции в математикеПрямая
Обратная
Сложение
x2
Возведение в квадрат
sin α = a
arcsin a = α a∈[-1;1]
Синус угла
Арксинус числа
Умножение
Деление
(xn)' = nxn-1
∫nxn-1dx = xn + C
Дифференцирование
Интегрирование
11.
Пояснение в сравненииПроизводная
Первообразная
"Производит" новую
функцию
Первичный образ
дифференцирование
интегрирование
вычисление производной
восстановление функции из
производной
12.
Определениепервообразной
y = F(x) называют первообразной для y = f(x)
на промежутке X, если при x ∈ X
F'(x) = f(x)
13.
Запомните: Первообразная – это родительпроизводной:
14.
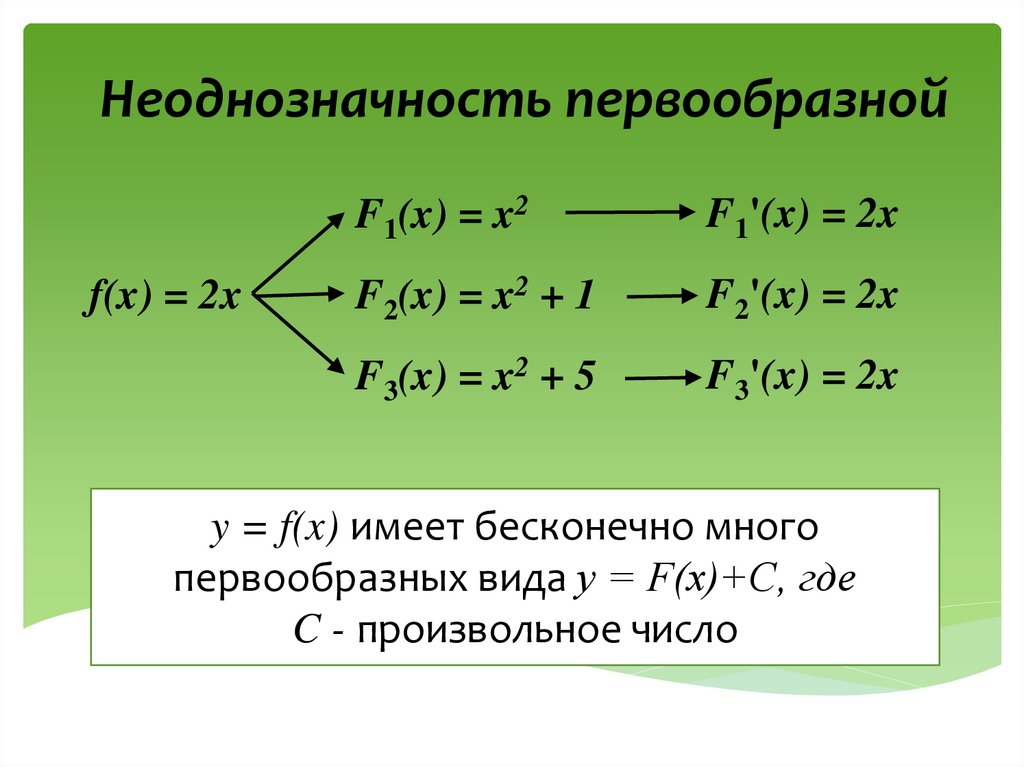
Неоднозначность первообразнойf(x) = 2x
F1(x) = x2
F1'(x) = 2x
F2(x) = x2 + 1
F2'(x) = 2x
F3(x) = x2 + 5
F3'(x) = 2x
y = f(x) имеет бесконечно много
первообразных вида y = F(x)+C, где
C - произвольное число
15.
Определение интегралаЕсли у функции y = f(x) на промежутке X есть
первообразная y = F(x), то все множества
функций вида y = F(x)+C называют
неопределенным интегралом от функции
y = f(x)
Обозначается как ∫f(x)dx
неопределенный интеграл f (эф) от x (икс) d (дэ) x (икс)
16.
Три правила нахождения первообразныхЕсли функции у=f(x) и у=g(x) имеют на
промежутке
первообразные соответственно у=F(x) и у=G(x), то
Функция
Первообразная
у = f(x) + g(x)
у = F(x) + G(x)
у =k f(x)
у =k F(x)
17.
Правила интегрирования18.
f(x)F(x)
1
k
kx+C
19.
Найти одну из первообразных дляследующих функций
1) f(x) = 4
1) F(x) = 4x
2) f(x) = -1
2) F(x) = -x
3) f(x) = x3




















 mathematics
mathematics








