Зачем нам нужен прямоугольный треугольник?

1.

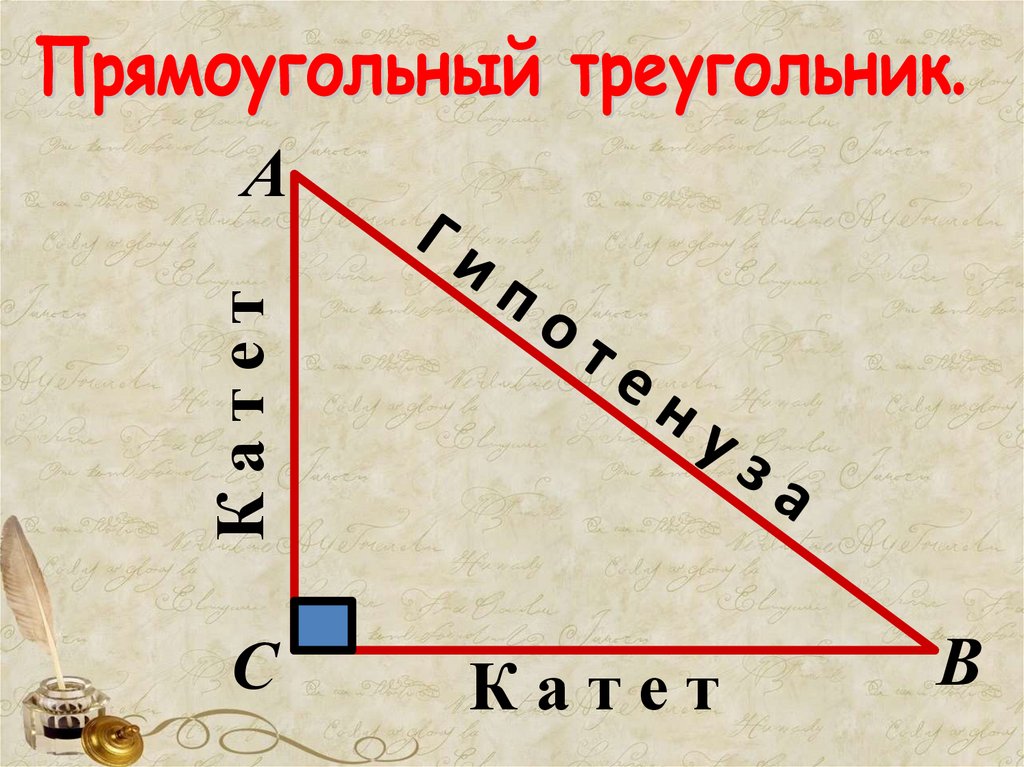
Катет
А
С
Катет
В

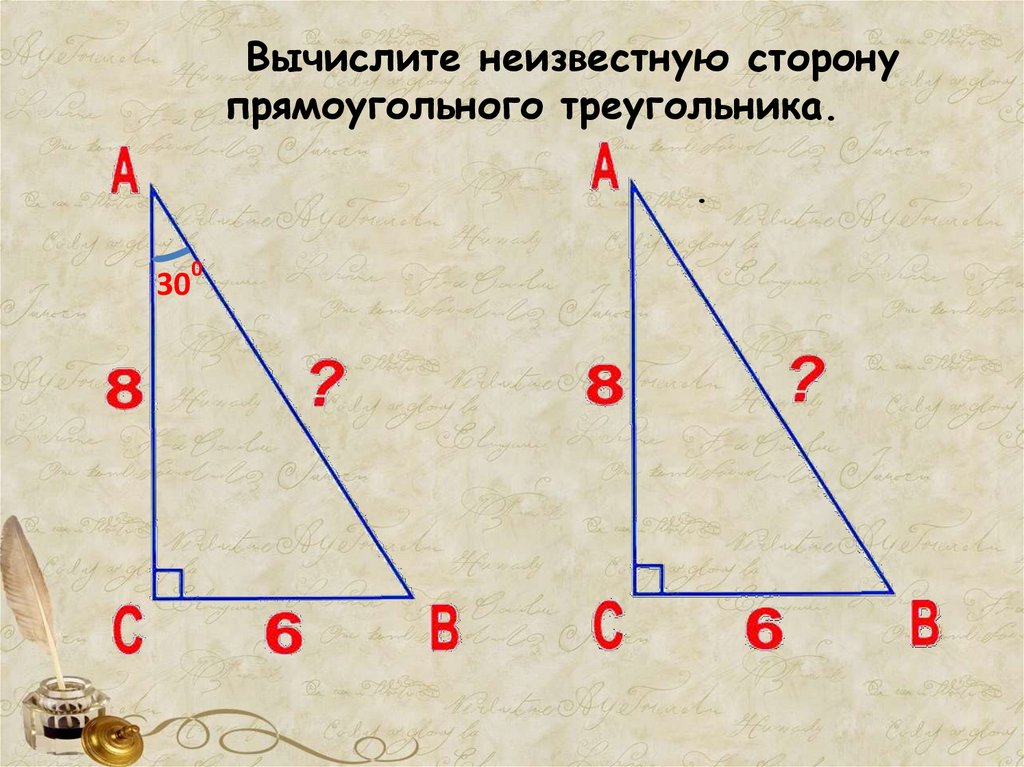
2. Вычислите неизвестную сторону прямоугольного треугольника.

.
0
30

3.

следили за светилами и по этим
наблюдениям вели календарь,
рассчитывали сроки сева,
время разлива рек;
корабли на море, караваны на
суше ориентировались в пути по
звездам.

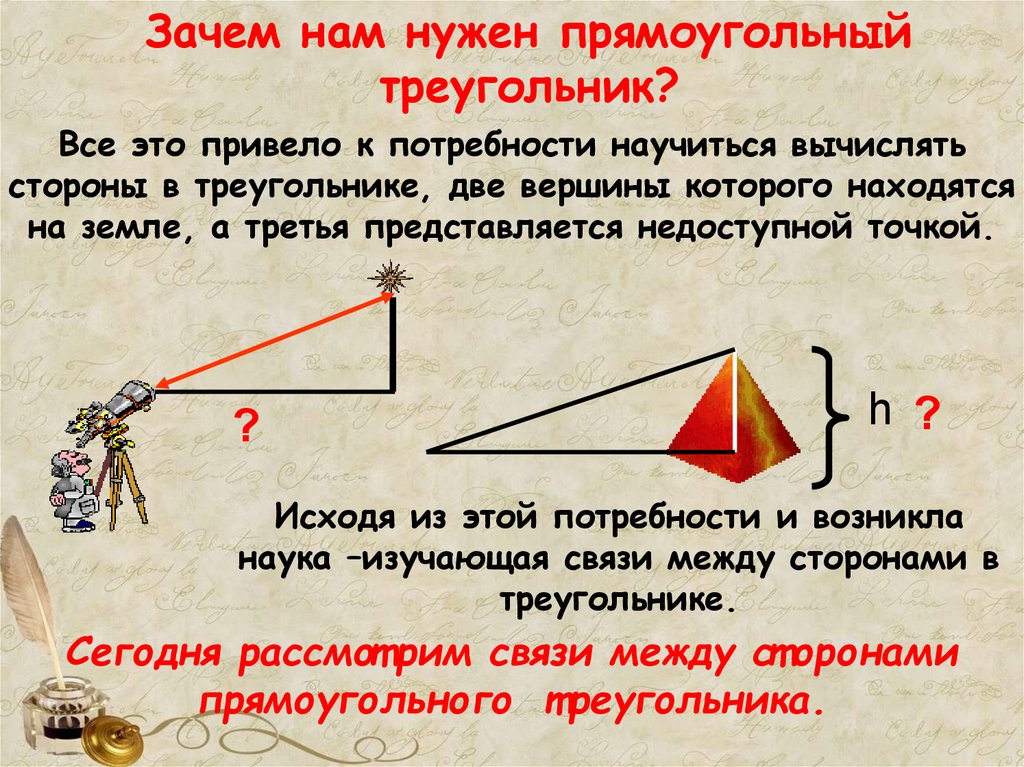
4. Зачем нам нужен прямоугольный треугольник?

Все это привело к потребности научиться вычислять
стороны в треугольнике, две вершины которого находятся
на земле, а третья представляется недоступной точкой.
?
h ?
Исходя из этой потребности и возникла
наука –изучающая связи между сторонами в
треугольнике.
Сегодня рассмот рим связи между ст оронами
прямоугольного т реугольника.

5.

МОУ СОШ № 5 г. Радужный

6.

" Все исследуй,
давай разуму
первое место".
Пифагор

7. Задачи урока:

Научиться формулировать
теорему Пифагора
Показать значимость теоремы
Пифагора при решении задач
Найти применение теоремы в
жизни человека

8. Исследовательская работа

Цель - установить
связь между сторонами
прямоугольного треугольника.
ЗАДАНИЕ:
Попробуйте найти связь между сторонами
прямоугольного треугольника и
сформулировать теорему Пифагора
Работа в парах
Время – 7 минут

9. Таблица квадратов

Х 2 3 4 5 6 7 8 9 10
2
Х 4 9 16 25 36 49 64 81 100

10. Инструкция

1) Исследовать прямоугольный треугольник с катетами
3см и 4см.
2) Измерить длину его гипотенузы
3) Внести в таблицу полученные данные квадратов
катетов и квадрата гипотенузы
4) Повторите ту же работу с двумя другими
треугольниками
5) Проанализируйте данные таблицы – сформулируйте
гипотезу
квадрат
катета 1
квадрат
катета 2
квадрат
гипотенузы
Связь между
сторонами
1.
9 см
16 см
25 см
9 + 16 = 25
2.
36 см
64 см
100 см
36 + 64=100
3.
25см
144 см
169см
25+ 144=169

11.

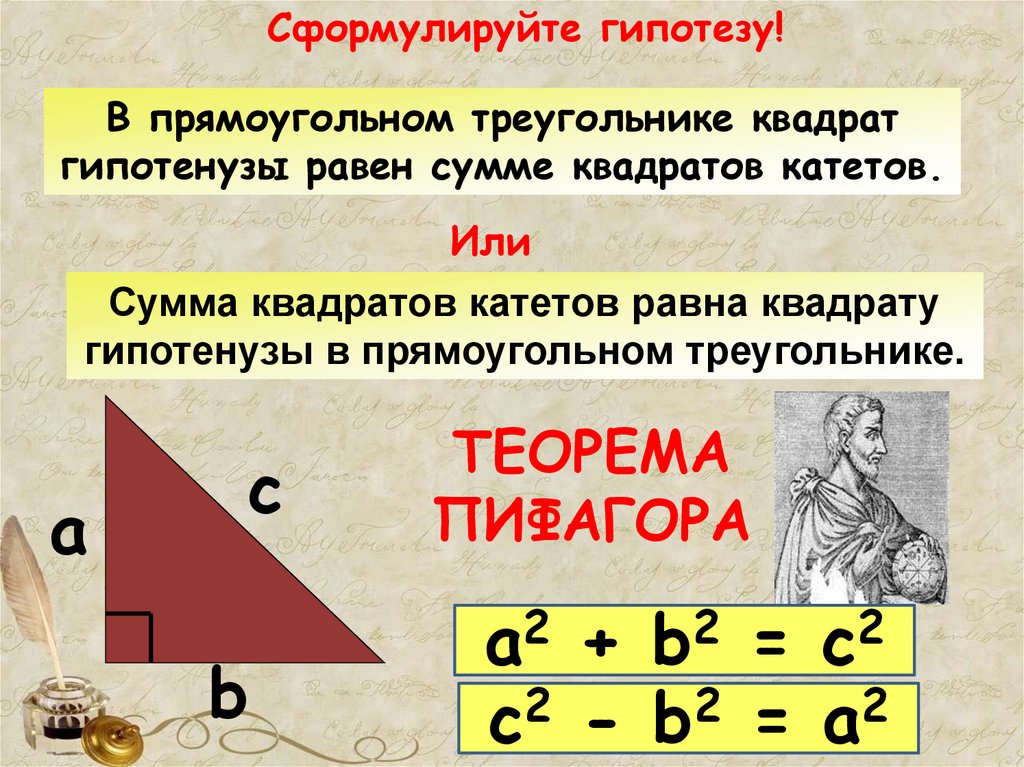
Сформулируйте гипотезу!
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Или
Сумма квадратов катетов равна квадрату
гипотенузы в прямоугольном треугольнике.
a
c
b
ТЕОРЕМА
ПИФАГОРА
a2 + b2 = c2
2
2
2
с - b = а

12. Лист самооценки

Выполнил
самостоятельно
Сформулировал
теорему
Пифагора
Решение задач
Практическое
применение
теоремы
Пифагора
3
С помощью
товарища
2
Только после
объяснения
учителя
1

13.

Немного истории
из жизни
Пифагора

14. Пифагор Самосский

Пифагор родился в 580г.
до н.э. на острове Самос,
в семье богатого
ювелира.
Знания, полученные им в
храмах Греции не давали
ответов на все
волнующие его вопросы,
и он отправился в
поисках мудрости в
Египет.

15.

В течение 22 лет он
проходил обучение в
храмах Египта, где
был посвящен в жрецы
Здесь он глубоко
изучил математику.
Около 530 года
Пифагор возвратился
в Грецию и вскоре
основал
Пифагорейский союз.

16.

Вот одна из заповедей:
Не делай никогда того,
что не знаешь, но
научись всему, что
следует знать, и тогда
будешь вести
спокойную жизнь

17.

Пифагорейцами было
сделано много важных
открытий в арифметике и
геометрии ,в том числе:
Теорема о сумме внутренних углов
треугольника
Построение правильных
многоугольников
Геометрические способы решения
квадратных уравнений
Создание математической теории
музыки
Около 40 лет Пифагор посвятил
созданной им школе, и в возрасте
80 лет по одной из версий он был
убит в уличной схватке во время
народного восстания

18. Решение задач

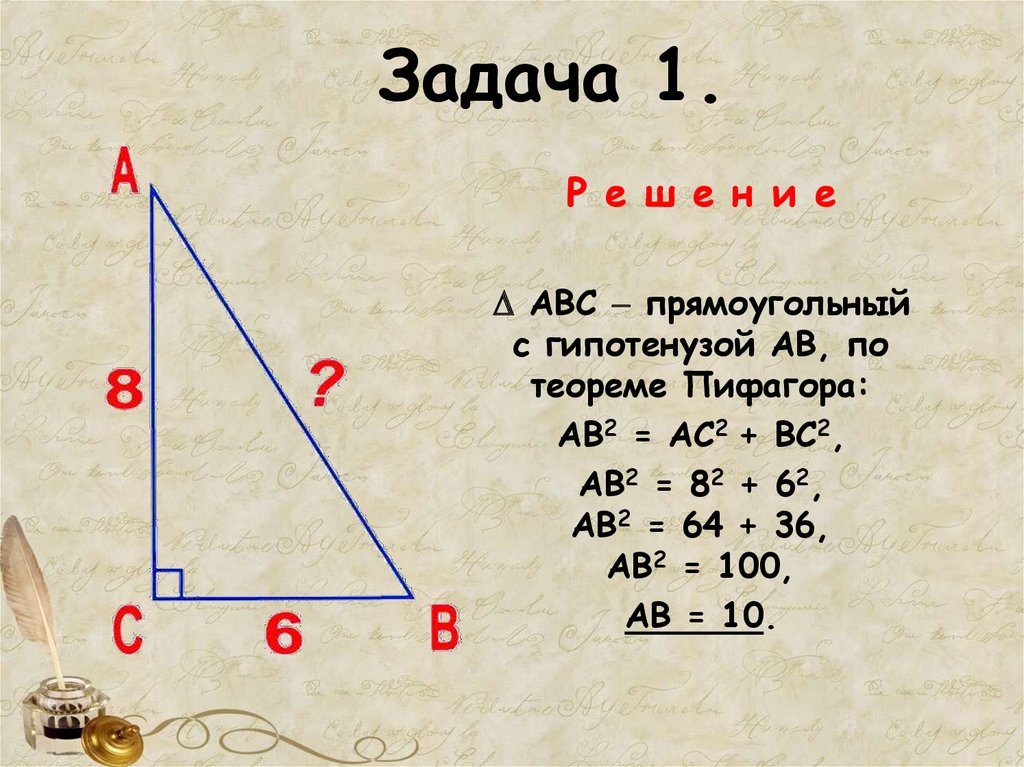
19. Задача 1.

Р е ш е н и е
АВС прямоугольный
с гипотенузой АВ, по
теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62,
АВ2 = 64 + 36,
АВ2 = 100,
АВ = 10.

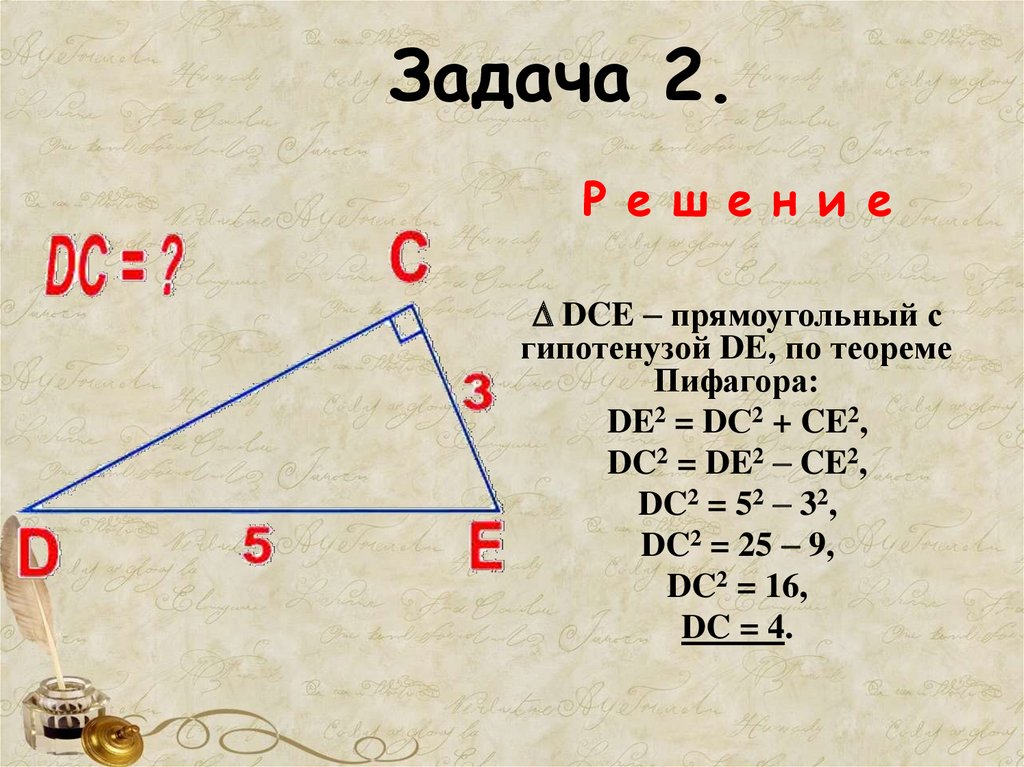
20. Задача 2.

Р е ш е н и е
DCE прямоугольный с
гипотенузой DE, по теореме
Пифагора:
DE2 = DС2 + CE2,
DC2 = DE2 CE2,
DC2 = 52 32,
DC2 = 25 9,
DC2 = 16,
DC = 4.

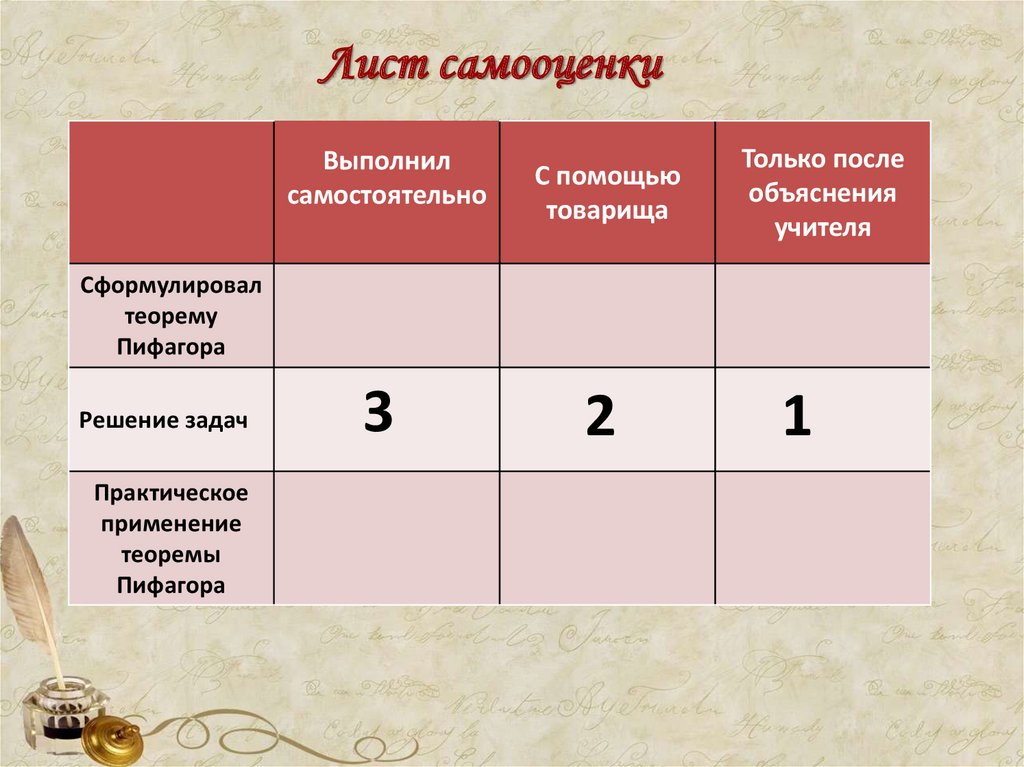
21. Лист самооценки

Выполнил
самостоятельно
С помощью
товарища
Только после
объяснения
учителя
Сформулировал
теорему
Пифагора
Решение задач
Практическое
применение
теоремы
Пифагора
3
2
1

22. Практическое применение теоремы Пифагора

23. Задача индийского математика XII века Бхаскары

На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

24.

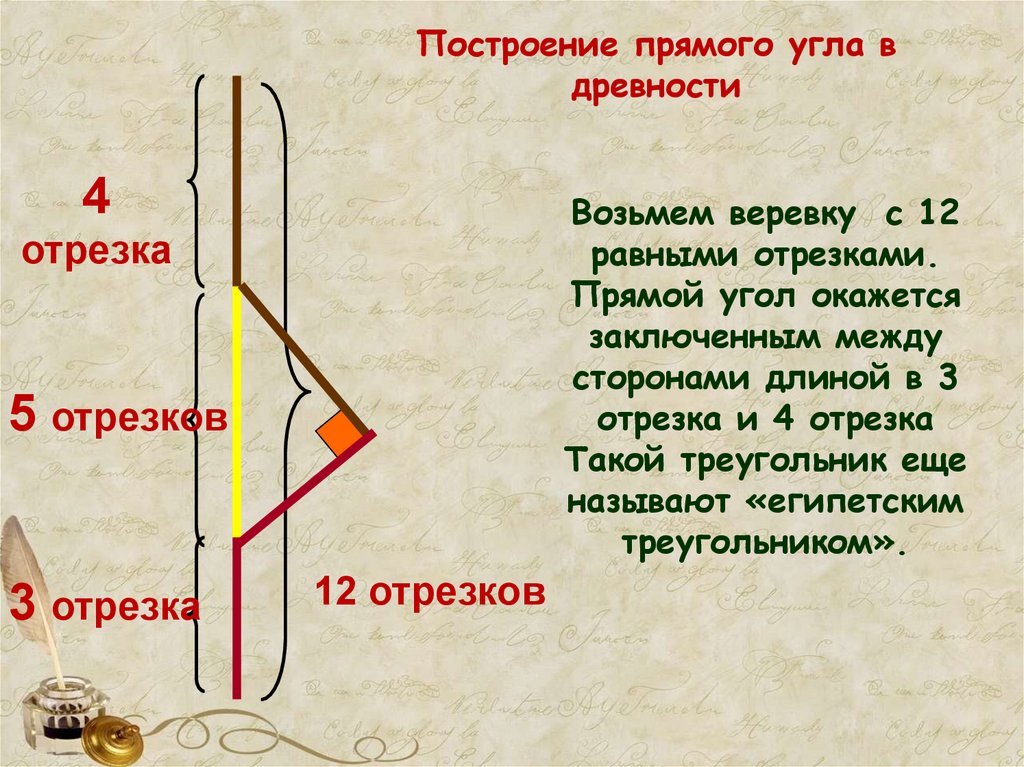
Построение прямого угла в
древности
4
Возьмем веревку с 12
равными отрезками.
Прямой угол окажется
заключенным между
сторонами длиной в 3
отрезка и 4 отрезка
Такой треугольник еще
называют «египетским
треугольником».
отрезка
5 отрезков
3 отрезка
12 отрезков

25. ПРОВЕРЬ СЕБЯ

26.

Египетский
треугольник
На веревке
отмеривались 3
последовательных
отрезка длиною в 3,
4 и 5 единиц
длины.
Если соединить
концы этой веревки
и натянуть ее на 3ем и 7-ом делении,
то получится
прямоугольный
треугольник.

27. Прямоугольные треугольники вокруг нас

28. Лист самооценки

Выполнил
самостоятельно
С помощью
товарища
Только после
объяснения
учителя
Сформулировал
теорему
Пифагора
Решение задач
Практическое
применение
теоремы
Пифагора
3
2
1

29. Теорема Пифагора - это одна из самых важных теорем геометрии.

Значение ее состоит в том, что из нее или с
ее помощью можно вывести большинство
теорем геометрии.
Теорема Пифагора - это первое
утверждение, связавшее длины сторон
треугольников.
Большинство задач решаются с помощью
теоремы Пифагора
Теорема Пифагора очень часто применяется
и в нашей реальной жизни: строительстве,
земледелии, астрономии, космонавтике и
т.д.

30. Подведем итоги:

31. Критерии оценки

Если ты набрал 8-9 баллов – оценка «5»
Если ты набрал 6-7 баллов - оценка «4»
Если ты набрал 3-5 баллов – оценка»3»

32. Домашнее задание

1.Познакомится с материалами
буклета
2.Попробовать решить несколько
исторических задач
3. Подготовить одно из 100
известных доказательств теоремы
Пифагора.

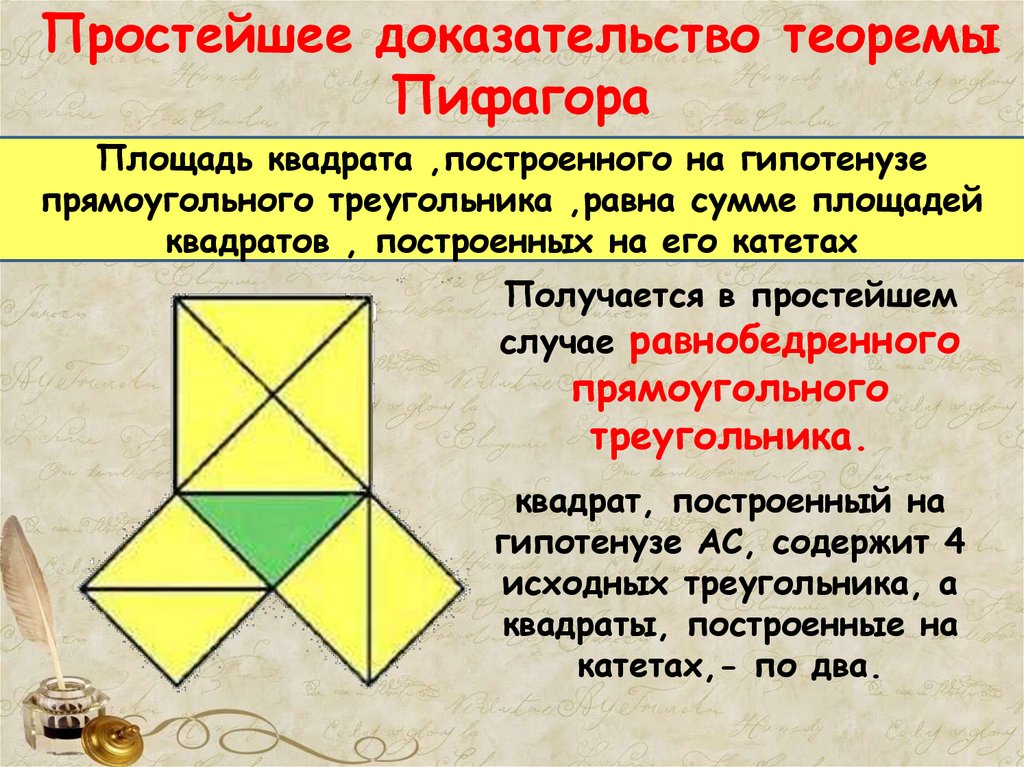
33. Простейшее доказательство теоремы Пифагора

Площадь квадрата ,построенного на гипотенузе
прямоугольного треугольника ,равна сумме площадей
квадратов , построенных на его катетах
Получается в простейшем
случае равнобедренного
прямоугольного
треугольника.
квадрат, построенный на
гипотенузе АС, содержит 4
исходных треугольника, а
квадраты, построенные на
катетах,- по два.

34.

В средние века знание теоремы Пифагора
говорило о хорошем уровне математических
знаний, а характерный чертеж к ней, который
школьниками превращается, например, в
облеченного в мантию профессора, становился
символом математики.

35. Популярность теоремы Пифагора столь велика , что ей посвящены стихи

Суть истины вся в том, что нам она – навечно
Когда хоть раз в прозрении ее увидим свет,
И теорема Пифагора через столько лет
Для нас , как для него, бесспорна,
безупречна…
(отрывок из стихотворения
А. Шамиссо)

36.

Спасибо
за урок!