Арифметические операции над числами в различных системах счисления

1. Арифметические операции над числами в различных системах счисления

Лекция № 2
Арифметические операции над
числами в различных системах
счисления
1

2. Сложение чисел

Правило № 6
При сложении двух чисел в системе счисления с
основанием q необходимо записать их столбиком одно над
другим так, чтобы соответствующие разряды одного
слагаемого располагался под соответствующими
разрядами другого слагаемого.
Сложение производится поразрядно справа налево,
начиная с младших разрядов слагаемых.
2

3. Сложение чисел (продолжение)

Рассмотрим сложение в разряде с номером i.
Введем обозначения: ai и bi - цифры соответственно первого и
второго слагаемых i-го разряда, pi -признак переноса единицы
из i - 1 разряда в i-ый разряд.
Признак переноса pi равен 1, если в i -1 разряде сформирована
единица переноса в i-ый разряд и равен 0 в противном случае.
Всегда: p0=0.
Найдем сумму: S = a+ b + pi;
a и b- десятичные числа, которые соответствуют цифрам ai и bi.
Сложение производиться в десятичной системе счисления.
3

4. Сложение чисел (окончание)

Возможны два случая:
1. S q.
Из S вычтем основание системы счисления q.
Сформируем признак переноса pi+1 в следующий i+1 разряд,
равный 1.
Разности, полученной в результате вычитания, поставим
в
соответствие цифру si системы счисления с основанием q.
2. S< q.
Сформируем признак переноса pi+1 в следующий i+1 разряд,
равный 0.
Поставим в соответствие десятичному числу S цифру si системы
счисления с основанием q.
Полученная цифра si является цифрой i-го разряда суммы.
Аналогично производится сложение в каждом разряде. 4

5. Пример сложения двоичных чисел

1
1
1
1
0
0
1
1
1
1
1
1
0
1
1
0
0
1
+
6
0
110
7
1
110
3
1
210
+
1
1
0
1
1
0
0
0
1
1
1
0
1
0
0
1
0
0
0
0
0
1
5

6. Пример сложения восьмеричных чисел

1
1
1
3
18
+
7
1
110
6
0
110
3
1
210
+
1
3
0
78
2
4
4
08
1
6

7. Пример сложения шестнадцатеричных чисел

1
1
2
5
916
+
7
1
110
6
0
110
3
1
210
+
2
с
716
5
2
016
1
7

8. Вычитание чисел в различных системах счисления

Правило № 7
(вычитаемое не больше уменьшаемого )
Для того чтобы вычесть числа в системе счисления
с основанием q, необходимо записать одно под другим
столбиком, чтобы разряды вычитаемого располагались
под соответствующими разрядами уменьшаемого.
Вычитание производиться поразрядно, начиная
с младшего разряда.
8

9. Вычитание чисел (продолжение)

Рассмотрим вычитание в i-ом разряде.
Введем обозначения:
ai и bi - цифры соответствующие уменьшаемому и вычитаемому
i-го разряда,
pi - признак единицы заёма i–го разряда.
Признак заёма pi равен -1, если возникла необходимость
в заёме единицы в предыдущем разряде
и признак pi равен 0 в противном случае.
Для нулевого разряда всегда выполняется p0 = 0.
9

10.

Вычитание чисел (продолжение)
Поставим в соответствии ai и bi
десятичные .числа a и b.
Найдем значение выражения
R = a b + pi.
10

11. Вычитание чисел (окончание)

Возможны два случая:
1. R 0.
Признаку заема присвоим значение равное –1: pi+1 = -1,
т.е. возникает заем единицы из следующего разряда.
Найдем сумму R + q.
Полученной сумме поставим в соответствие цифру
ri системы счисления с основанием q.
2. R 0.
Значению R необходимо поставить в соответствие цифру
r i.
Признаку заема присвоить значение равное нулю: pi+1 = 0.
Полученная цифра ri является цифрой i-го разряда разности.
11
Аналогично производится вычитание в каждом разряде.

12. Пример вычитания двоичных чисел

Необходимо вычесть из двоичного числа 1001011001
двоичное число 1011000111.
-1
-1
-1
-1
1
0
1
1
0
0
0
1
1
1
7
1
110
1
0
0
1
0
1
1
0
0
1
6
0
110
1
1
0
1
1
1
0
1
1
010
Итак, 1001011001 2 – 1011000111 2 = - 11011102
12

13. Пример вычитания восьмеричных чисел

-1
1
3
0
78
-
7
1
110
1
1
3
18
6
0
110
1
5
68
1
1
010
13

14. Пример вычитания шестнадцатеричных чисел

-1
2
с
716
_
7
1
110
_
2
5
916
6
0
110
6
е16
1
1
010
14

15. Умножение двоичных чисел (правило № 8)

Для того, чтобы умножить одно двоичное число
на другое необходимо записать их одно под другим,
чтобы разряды второго сомножителя располагался
под соответствующими разрядами первого сомножителя.
Назовем первый сомножитель - множимое,
а второй сомножитель - множитель.
15

16. Умножение двоичных чисел (продолжение)

Сформируем столбик чисел и расположим
его под записанными сомножителями.
Количество чисел столбика равно
количеству единиц множителя.
Каждое число столбика соответствует одной единице
множителя и образуется из записи множимого.
Множимое записывается в строке столбика
так, что его младший разряд располагается
под соответствующей единицей множителя.
Незаполненный элемент строки считается равным нулю.
16

17. Умножение чисел (окончание)

Образованный столбик чисел складывается.
При этом первоначально складываются первые два числа.
К результату сложения прибавляется третье число,
к очередному результату прибавляется четвертое число,
и т. д.
Полученная сумма является произведением
двух исходных чисел.
17

18. Пример умножения двоичных чисел

1
4
1
3
1
2
1
1
1
0
9
8
7
6
5
4
3
2
1
0
1
0
0
1
0
1
1
0
0
1
6
0
1
3
6
6
1
0
0
1
0
0
1
1
0
0
1
0
1
1
0
0
+
1
0
0
1
0
1
1
0
0
1
1
0
1
0
1
0
0
1
0
0
+
0
0
1
0
0
3
6
0
1
8
0
3
2
1
6
3
18
6

19. Деление двоичных чисел (правило № 9)

Для того, чтобы разделить одно двоичное число на другое
необходимо записать числа также как записываются числа
при делении в десятичной системе счисления (уголком).
1. Просматриваем делимое слева направо,
начиная со старшего разряда,
и определим минимальную по длине
последовательность нулей и единиц,
из которой можно образовать число не меньшее, чем
делитель.
19

20.

Деление двоичных чисел (продолжение)
2. Запишем под образованным числом делитель
таким образом, чтобы младший разряд делителя
располагался под младшим разрядом
образованного числа.
3. Выполним вычитание, т.е. из образованного
числа вычтем делитель и найдем разность.
4. В область частного запишем единицу.
Если в области частного имеется
последовательность цифр,
то единица приписывается
справа к последовательности цифр,
размещенной в области частного.
20

21. Деление двоичных чисел (продолжение)

5. Припишем справа к полученной разности разряд
делимого расположенный за образованным числом.
Если такой разряд отсутствует, то деление закончено
и образованное из разности
и возможно приписанных справа к разности ранее
разрядов делимого число является остатком от деления.
21

22.

Деление двоичных чисел (продолжение)
Если разряд делимого можно приписать к разности,
то возможны два случая:
5.1. Образованное число меньше делителя. В этом случае
в область частного необходимо справа приписать ноль и
повторить шаг 5.
5.2. Образованное число больше или равно делителя.
В этом случае следует вновь выполнить шаги 2, 3, 4, 5.
22

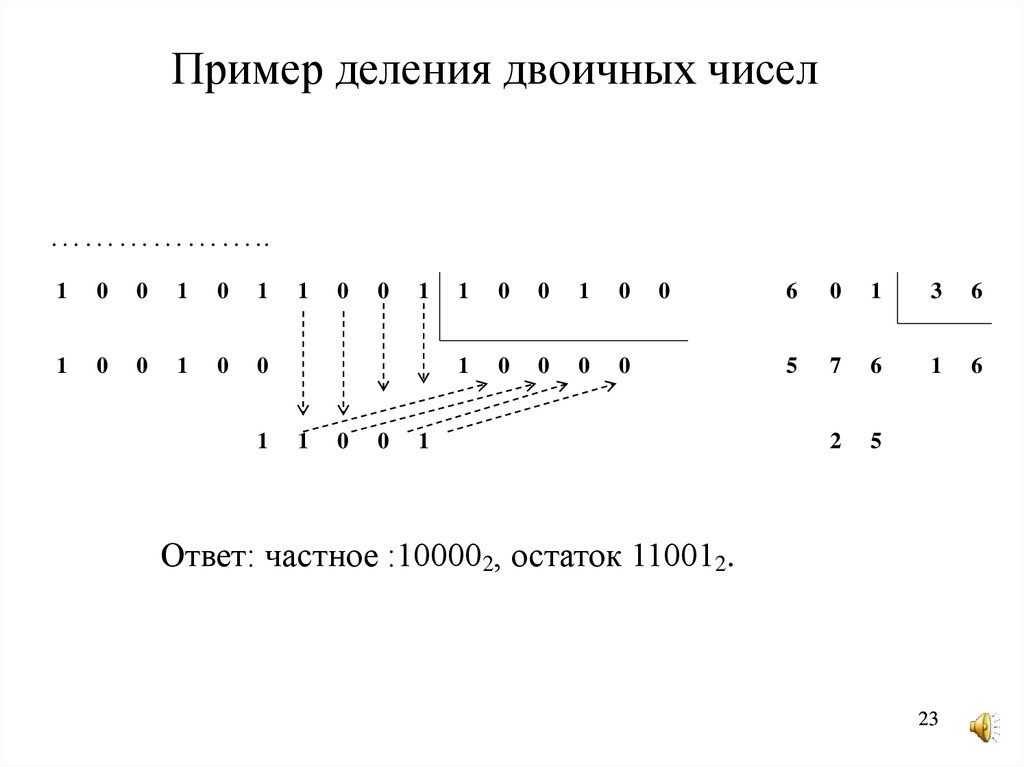
23. Пример деления двоичных чисел

………………..
1
0
0
1
0
1
1
0
0
1
0
0
1
1
1
0
0
0
0
1
1
0
0
1
0
1
0
0
0
0
0
1
6
0
1
3
6
5
7
6
1
6
2
5
Ответ: частное :100002, остаток 110012.
23

24. Заключение к лекции

1. Сложение чисел в различных системах
счисления.
2. Вычитание чисел в различных системах
счисления.
3. Умножение двоичных чисел.
4. Деление двоичных чисел.
24