Similar presentations:
Решение задач на применением признаков равенства треугольников (7 класс)
1. Урок по геометрии в 7 классе «Решение задач на применением признаков равенства треугольников»
учитель математики МОУ СОШ № 42Береля Людмила Николаевна
Краснодар
2009
2. эпиграф
Если вы хотите научитьсяплавать, то смело идите в воду, а
если хотите научиться решать
задачи – решайте их.
Д. Пойа, «Математическое
открытие»
3. Цели урока
Знать: формулировки признаков, определение исвойства равнобедренного треугольника и его
элементов.
Уметь: применять полученные знания в решении
задач на доказательство и на вычисления
4. Ход урока
Повторить:• 1) определение равнобедренного
треугольника
• 2) свойства равнобедренного треугольника
• 3)признаки равенства треугольников
5. Устно:
TЗадание 1
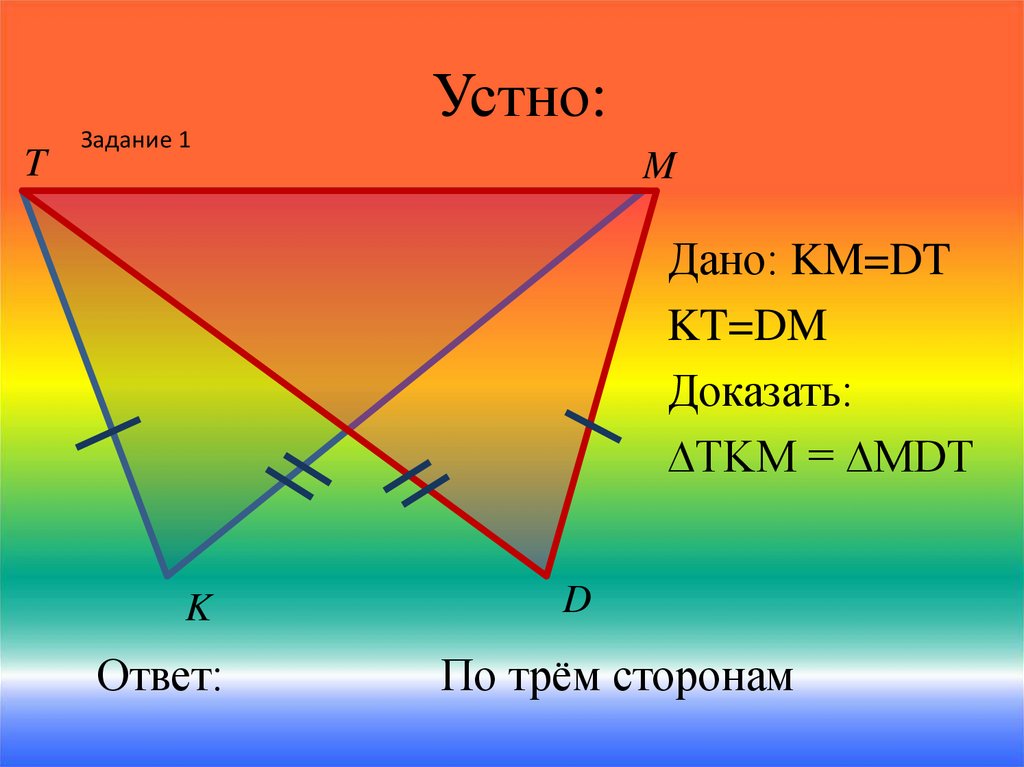
Устно:
M
Дано: KM=DT
KT=DM
Доказать:
∆TKM = ∆MDT
K
Ответ:
D
По трём сторонам
6.
Дано: AO = 4 см,BC = 5 см, CD
= 4,5 см.
Найти: Р
Задание 2
A
ABO
O
C
B
D
Ответ: ∆АВО = ∆DOC по стороне и двум прилежащим к ней углам, РABO = 11 см.
7.
Задание 3E
C
Дано: < EDC = < KDC,
DE = DK, < EDC =30°
Найти: < ECK
K
D
Ответ: < ECD = < KCD = 30°
< ECK = 60°
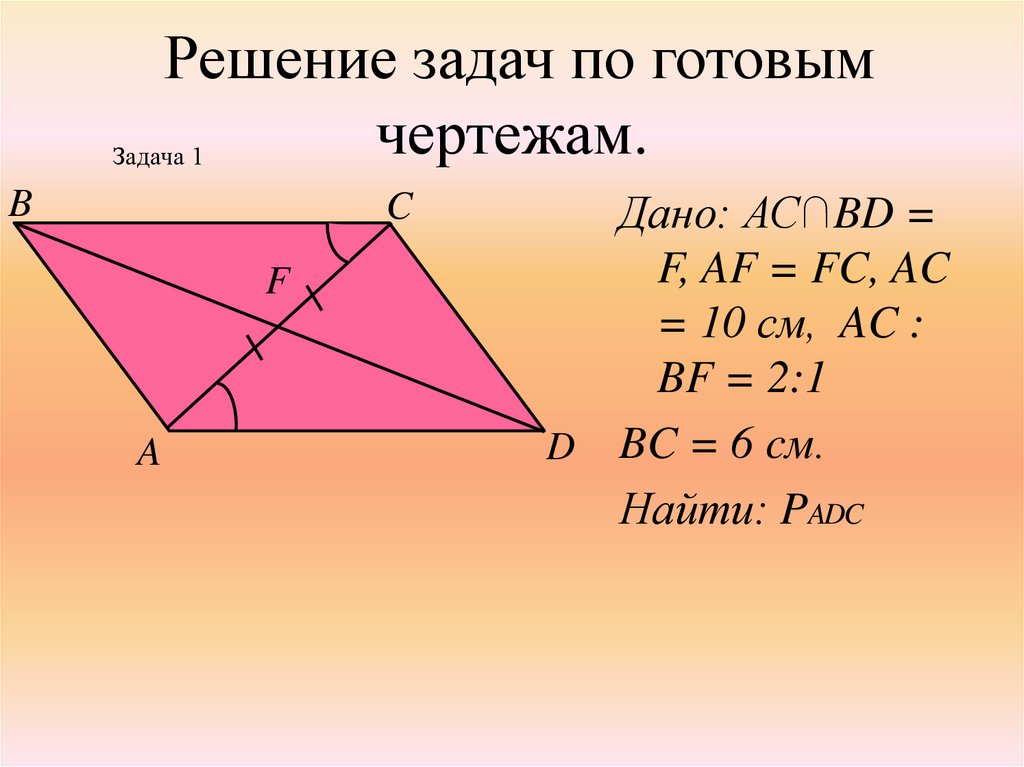
8. Решение задач по готовым чертежам.
Задача 1B
C
F
A
Дано: АС∩BD =
F, AF = FC, AC
= 10 см, AC :
BF = 2:1
D BC = 6 cм.
Найти: PADC
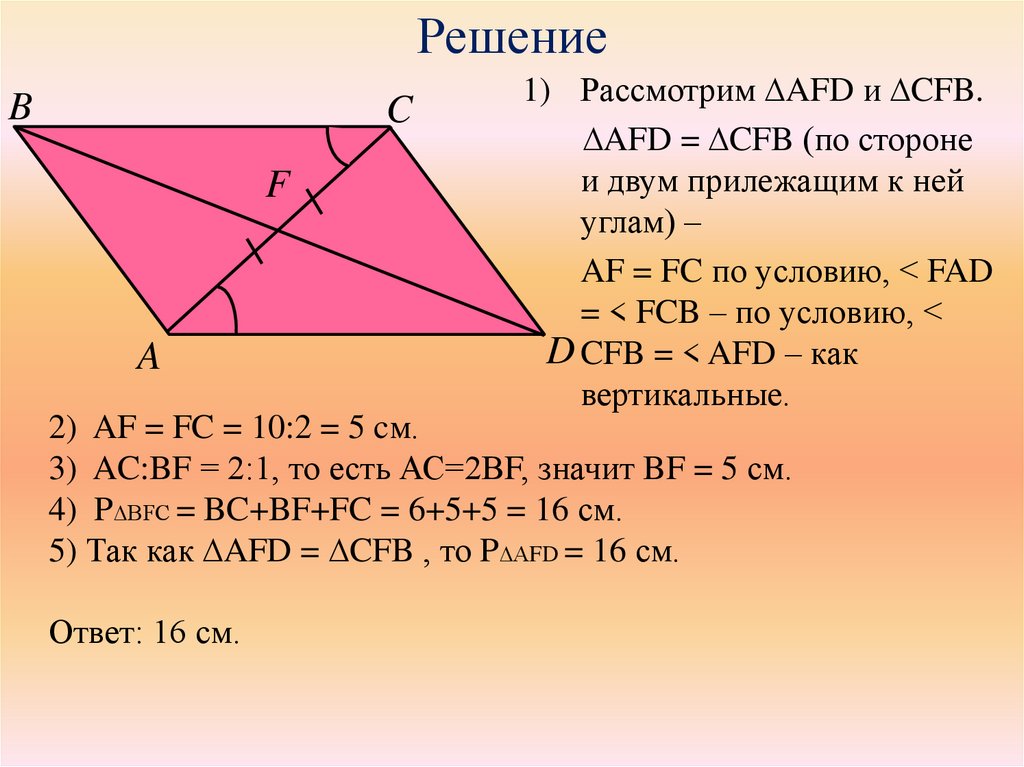
9. Решение
BC
F
A
1) Рассмотрим ∆AFD и ∆CFB.
∆AFD = ∆CFB (по стороне
и двум прилежащим к ней
углам) –
AF = FC по условию, < FAD
= < FCB – по условию, <
D CFB = < AFD – как
вертикальные.
2) AF = FC = 10:2 = 5 cм.
3) AC:BF = 2:1, то есть АС=2ВF, значит BF = 5 см.
4) P∆BFC = BC+BF+FC = 6+5+5 = 16 см.
5) Так как ∆AFD = ∆CFB , то P∆АFD = 16 см.
Ответ: 16 см.
10.
Задача 2B
1
2
3
4
C
D
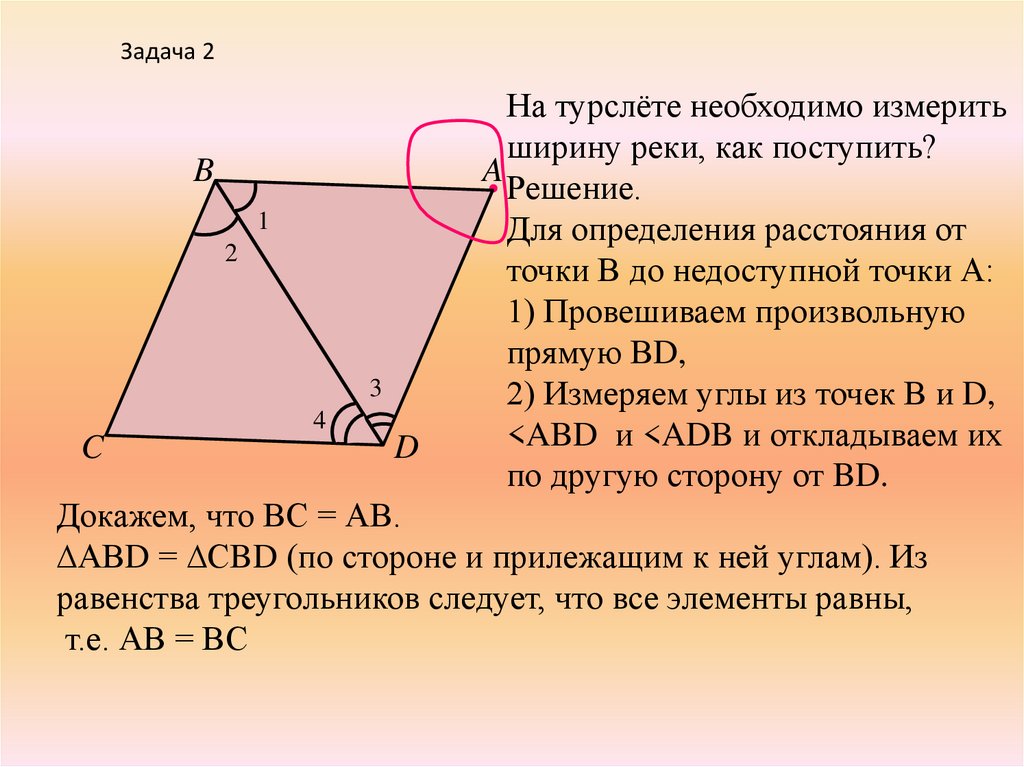
На турслёте необходимо измерить
ширину реки, как поступить?
A
Решение.
Для определения расстояния от
точки В до недоступной точки А:
1) Провешиваем произвольную
прямую ВD,
2) Измеряем углы из точек В и D,
<ABD и <ADB и откладываем их
по другую сторону от BD.
Докажем, что ВС = АВ.
∆АВD = ∆СBD (по стороне и прилежащим к ней углам). Из
равенства треугольников следует, что все элементы равны,
т.е. АВ = ВС
11. Исторический материал
Любой геометрическийматериал возник из потребностей
окружающей жизни.
Доказательство признаков
равенства треугольников
приписывают древнегреческому
ученому Фалесу Милетскому
(жившему ок.625-547г.г до н.э.).
Теорему о равенстве
треугольников по стороне и
прилежащим к ней двум углам он
использовал для определения
расстояния от берега до морских
кораблей.
12. V Самостоятельная работа
I вариант40°
B
D
A
II вариант
C
Задача 1
B
Дано:
АВ = СВ
DC = DA
< C = 40°
1) Доказать:
∆ABD = ∆CBD
2) BD биссектриса
<В
3) Найти < А
Задача 2
В треугольнике АВС
проведена медиана ВЕ. Найдите
длину АЕ, если АВ = 6 см,
периметр треугольника АВС равен
18 см, а ВС на 2 см больше АВ
C
A
Задача 1
Дано:
АD = AВ
120° CD = CB
D < D = 120°
1) Доказать:
∆DAC = ∆BAC
2) AC биссектриса
<В
3) Найти < В
Задача 2
В треугольнике АВС
проведена медиана АМ. Найдите
периметр треугольника АВС,
если ВМ = 4 см, АВ = 5 см, а АС
в 2 раза больше АВ
13. 6. Итоги урока
• Выставление оценок.14. Домашнее задание
пп. 17-20№ 119, 130, 138
Придумайте самостоятельно или найдите в
литературе,как можно измерить длину острова
, используя признаки равенства треугольников.
15. Используемая литература
• А.С. Атанасян и др.Геометрия 7-9 чебникдля общеобразовательных школМ.:Просвещение,2004
• Дидактический материал составитель
• А.П. Ершова,Илекса Москва,2006г.
• А.И.Медяник Методическое пособие по
геометрии 711классы,Москва,Издательский дом
«Дрофа»1996г.
• Я.Иперельман.Занимательная математика.










 mathematics
mathematics








