Простейшие тригонометрические уравнения (tg x = t, ctg x = t)

1.

Простейшие
тригонометрические
уравнения (tg x = t, ctg x = t).

2.

Решение уравнения sin t = а.
1) sin t = а , где | а | 1
не имеет решений
2) sin t = а , где | а | ≤ 1
или
Частные случаи
1) sin t = 0,
t = 0 + πk‚ k Є Z
2) sin t = 1,
t = π/2+2πk‚ k Є Z
3) sin t = – 1,
t= -π/2 + 2πk‚k Є Z

3.

Решение уравнения cos t = а.
1) cos t = а , где | а | 1
Частные случаи
не имеет решений
1) cos t = 0,
t = π/2+πk‚ k Є Z
2) cos t = а , где | а | ≤ 1
или
2) cos t = 1,
t = 0 + 2πk‚ k Є Z
3) cos t = – 1,
t = π + 2πk‚ k Є Z

4.

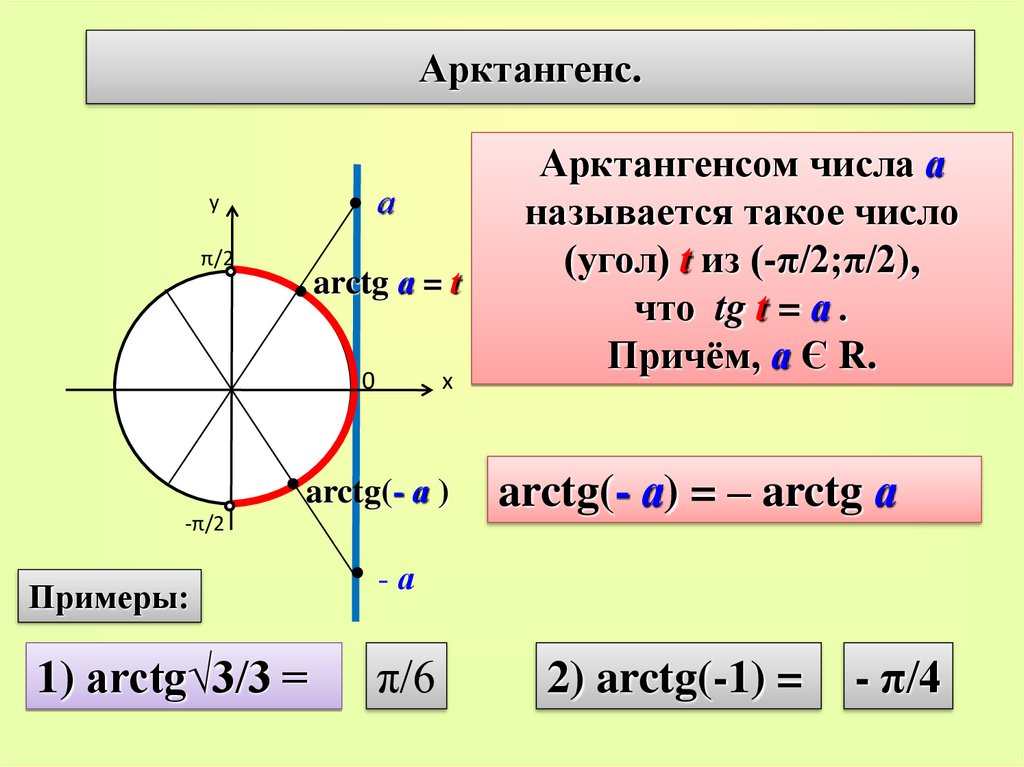
Арктангенс.
а
у
π/2
arctg а = t
0
х
arctg(- а )
-π/2
Примеры:
1) arctg√3/3 =
Арктангенсом числа а
называется такое число
(угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.
arctg(- а) = – arctg а
-а
π/6
2) arctg(-1) =
- π/4

5.

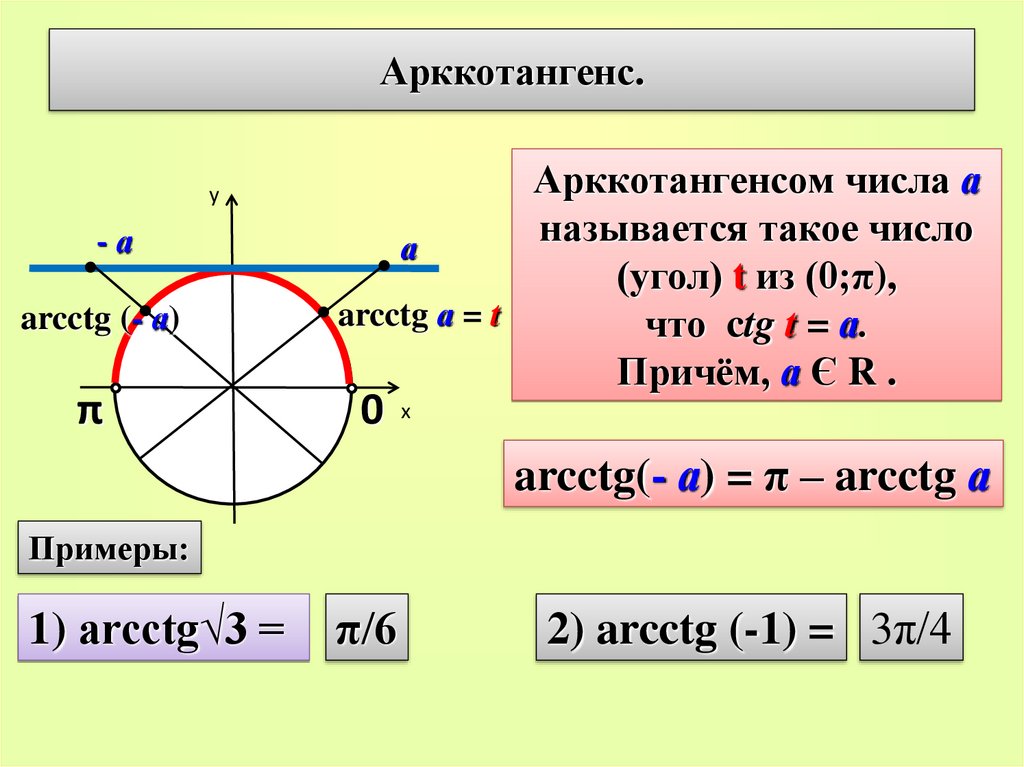
Арккотангенс.
у
-а
arcctg (- а)
π
Арккотангенсом числа а
называется такое число
а
(угол) t из (0;π),
arcctg а = t
что ctg t = а.
Причём, а Є R .
0
х
arcctg(- а) = π – arcctg а
Примеры:
1) arcctg√3 =
π/6
2) arcctg (-1) = 3π/4

6.

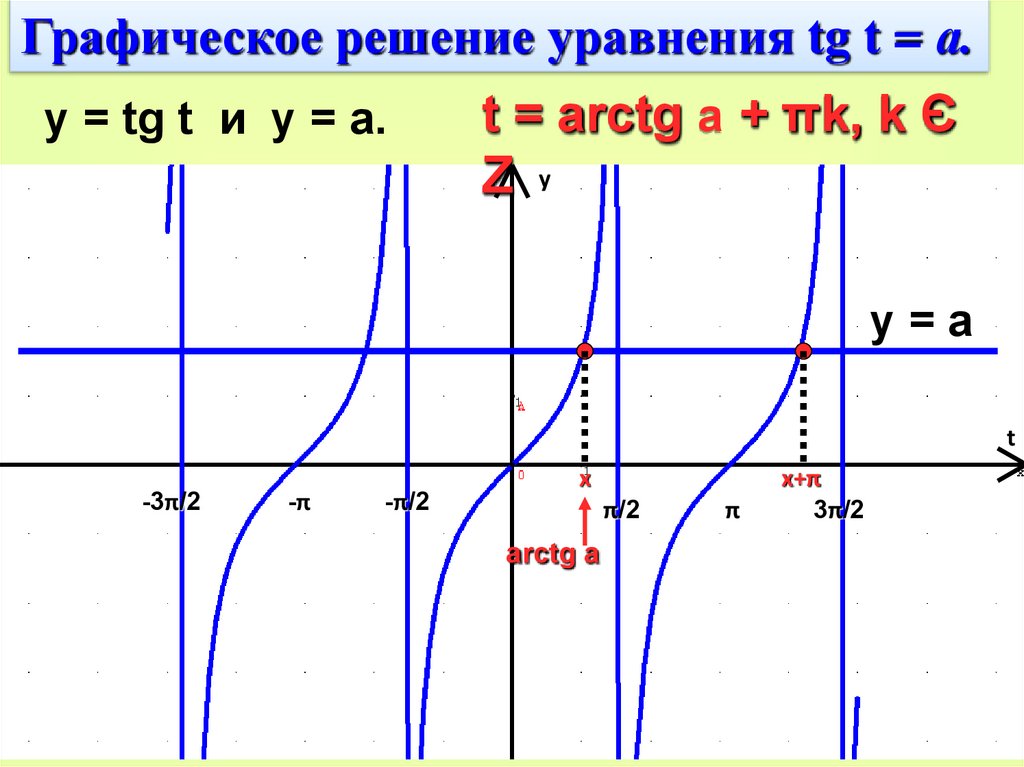
Графическое решение уравнения tg t = а.
y = tg t и y = a.
t = arctg a + πk‚ k Є
Z y
y=a
t
-3π/2
-π
-π/2
x
π/2
arctg a
π
x+π
3π/2

7.

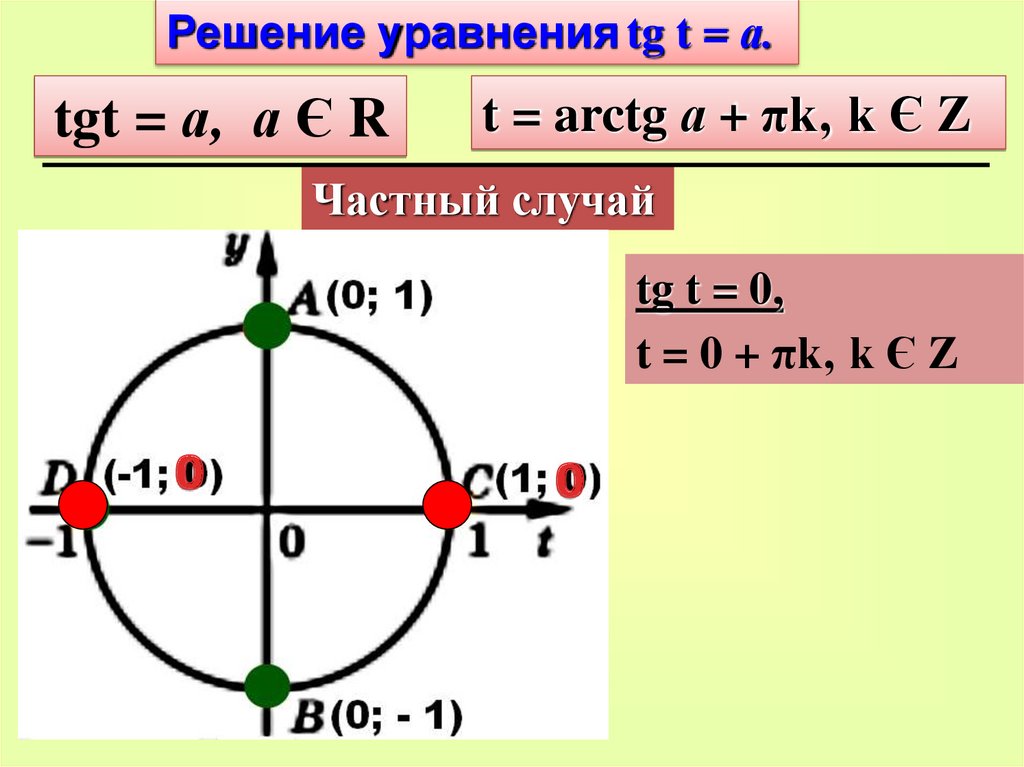
Решение уравнения tg t = а.
tgt = а, а Є R
t = arctg а + πk‚ k Є Z
Частный случай
tg t = 0,
t = 0 + πk‚ k Є Z
0
0

8.

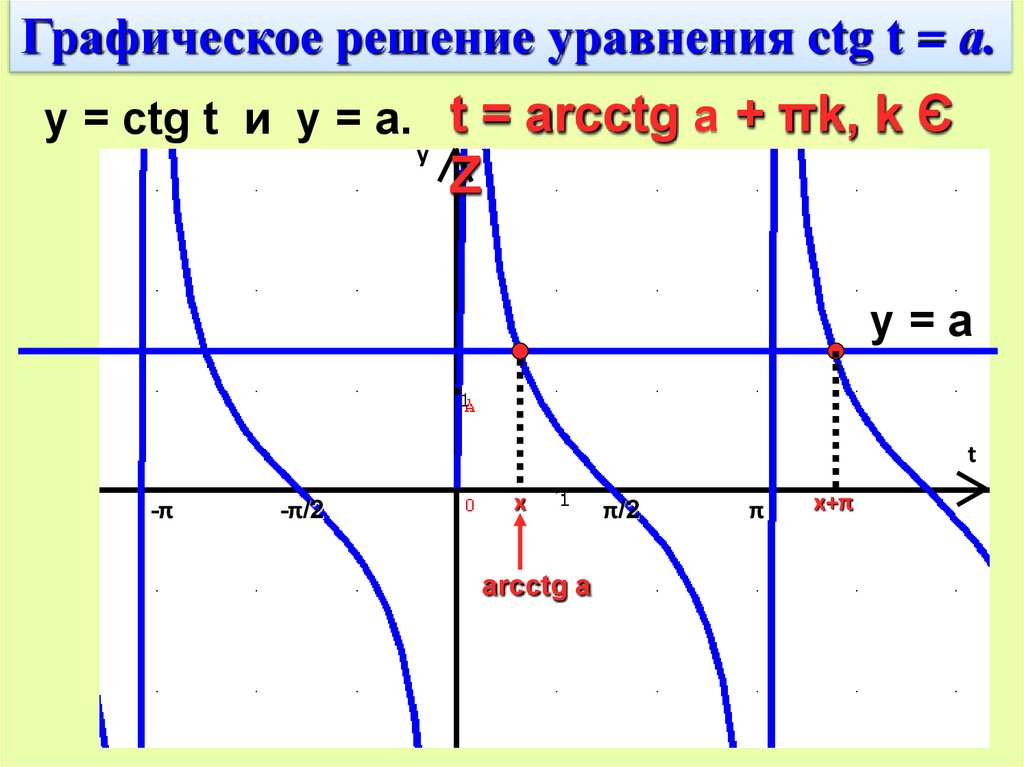
Графическое решение уравнения ctg t = а.
y = ctg t и y = a. t = arcctg a + πk‚ k Є
y
Z
y=a
t
-π
-π/2
x
arcctg a
π/2
π
x+π

9.

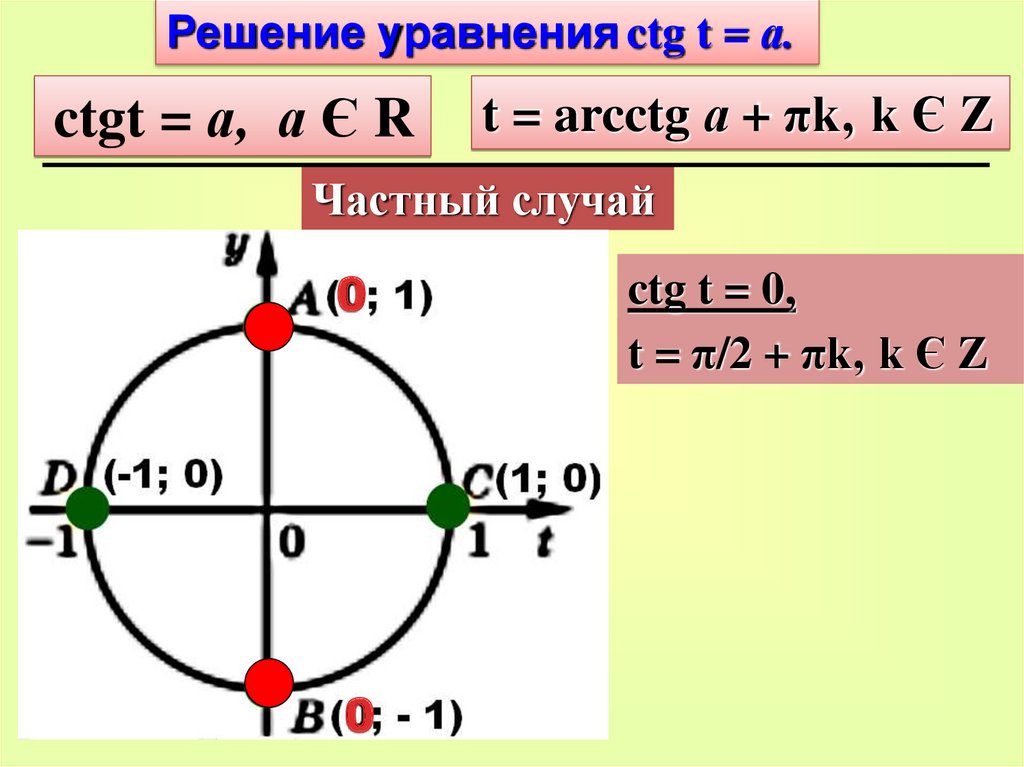
Решение уравнения ctg t = а.
ctgt = а, а Є R
t = arcctg а + πk‚ k Є Z
Частный случай
0
0
ctg t = 0,
t = π/2 + πk‚ k Є Z