Similar presentations:
Описательная статистика: основные статистические показатели
1.
Описательная статистика:основные статистические
показатели
2.
Статистические показатели• Применяется для метрических шкал, реже для
ранговых и порядковых;
• Анализируются три основных «показателя» в
рамках существующих ответов по шкале:
средние тенденции, разброс значений,
наличие отклонений от нормального
распределения;
• Связано с математическими представлением о
случайных величинах и их нормальном
распределении;
3.
МЕРЫ ЦЕНТРАЛЬНЫХТЕНДЕНЦИЙ
4.
Среднее (арифметическое)• Простое среднее арифметическое всех
значений ответов, полученных в ходе
опроса.
• Формула:
5.
Средняя взвешенная• Сумма произведений каждого ряда на ее
вес, разделенная на сумму весов:
6.
Средняя взвешеннаяЧисло детей
Число женщин
Число детей с учетом колва женщин
1
46
46
2
22
44
3
17
51
4
2
8
Кол-во жен. (ш) = 87
Кол-во дет. (∑ш*х)=149
Среднее число детей у одной женщины = 149/87=1,71,
т.е. в среднем по выборке на одну жен. приходится 1,71 ребенок.
7.
Медиана• «середина» упорядоченного по
возрастанию ряда;
Пример:
3516283526789 (13 ответов)
1223355667889 (13 ответов)
медиана =5
135628327899 (12 ответов)
122335!678899 (12 ответов)
медиана = (5+6)/2 = 5,5
8.
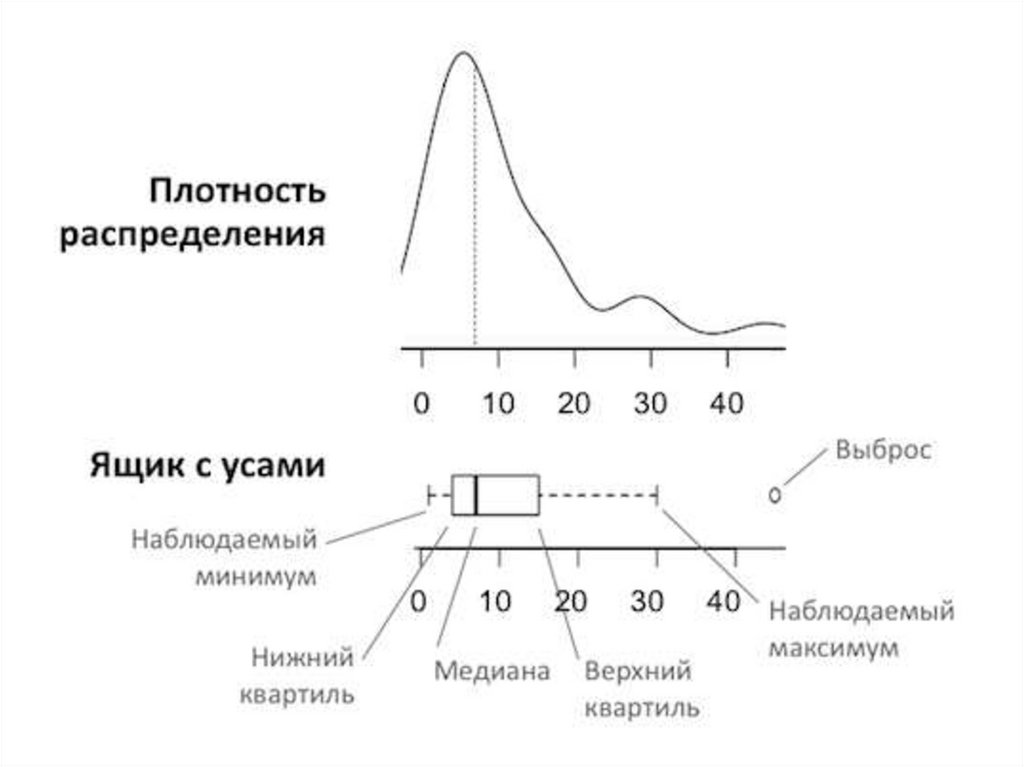
Квартили• Всего 3 стандартных квартиля: 25%, 50%,
75%;
• Квартиль в 50% - медиана;
Пример:
12233!56788
9.
10.
Анализ рядов11.
Мода• Самое часто встречаемое значение среди
ответов;
Пример:
1157281856156731
1111123555667788
12.
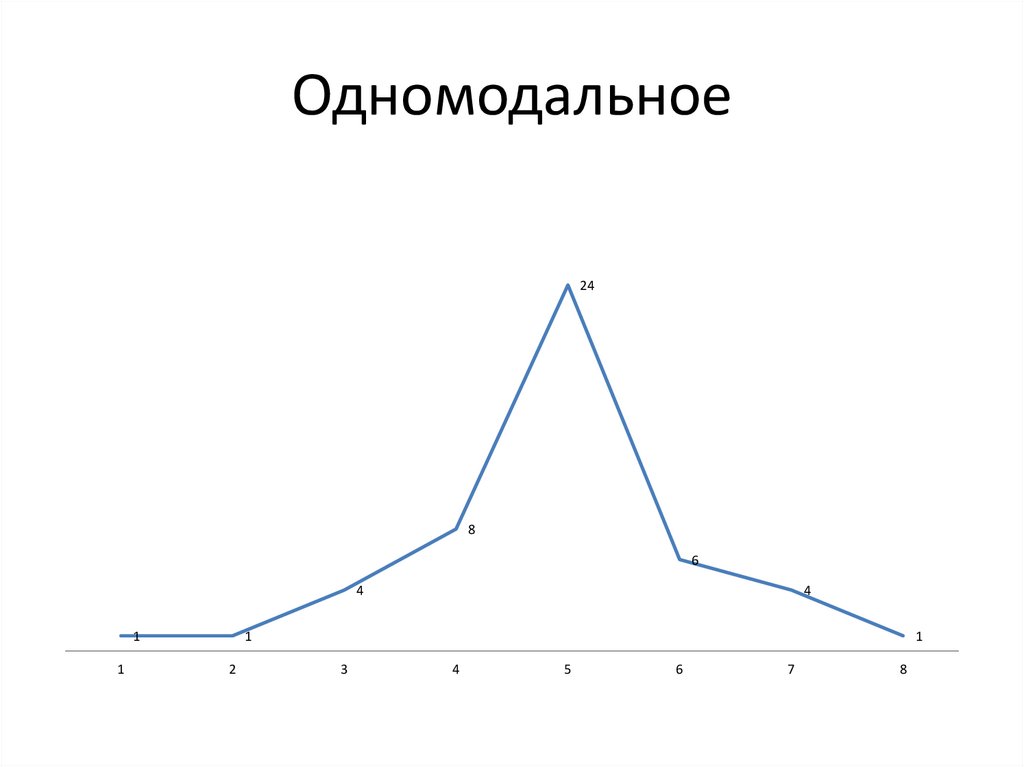
Одномодальное24
8
6
4
1
1
4
1
2
1
3
4
5
6
7
8
13.
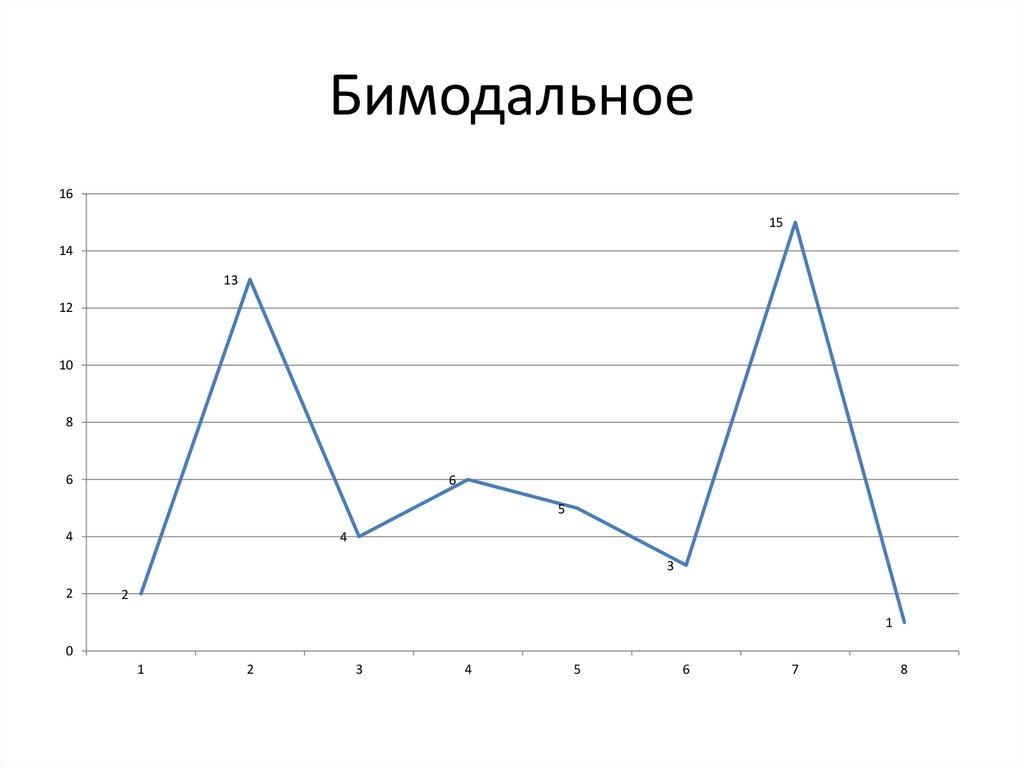
Бимодальное16
15
14
13
12
10
8
6
6
5
4
4
3
2
2
1
0
1
2
3
4
5
6
7
8
14.
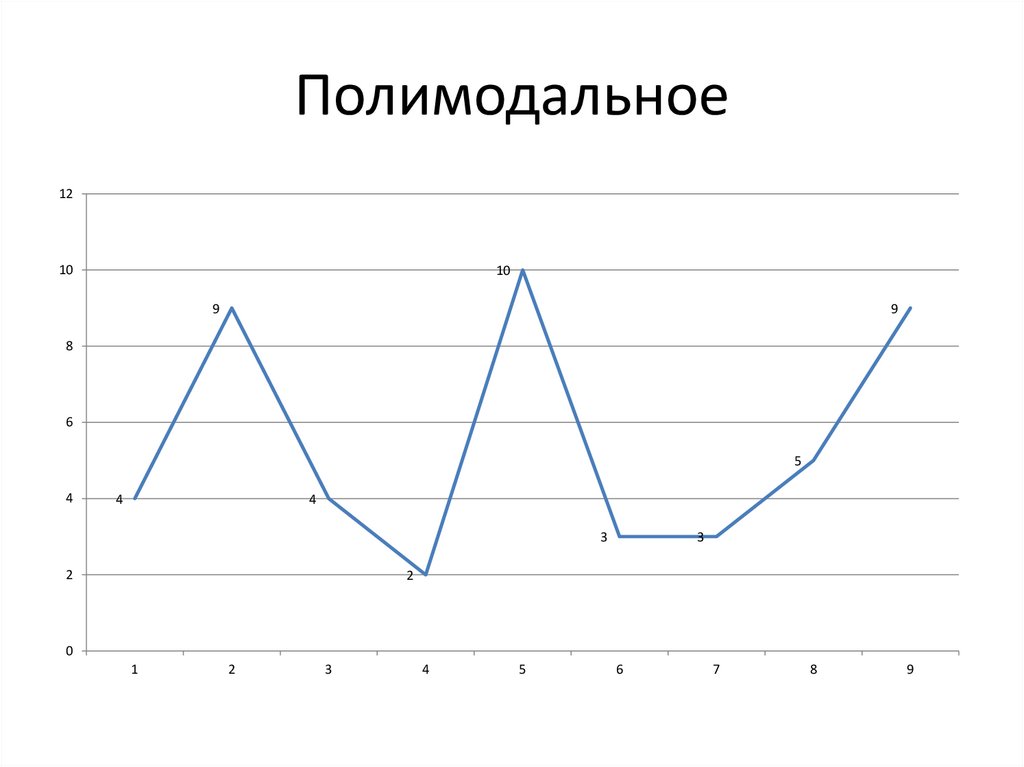
Полимодальное12
10
10
9
9
8
6
5
4
4
4
3
2
3
2
0
1
2
3
4
5
6
7
8
9
15.
МЕРЫ РАЗБРОСА ЗНАЧЕНИЙ16.
Дисперсия― среднее арифметическое возведённых в
квадрат расстояний от среднего значения до
каждой точки данных;
• Квадратный корень из дисперсии –
среднеквадратичное отклонение или
стандартное отклонение или стандартный
разброс;
• Стандартное отклонение – среднее расстояние
от среднего арифметического значения;
17.
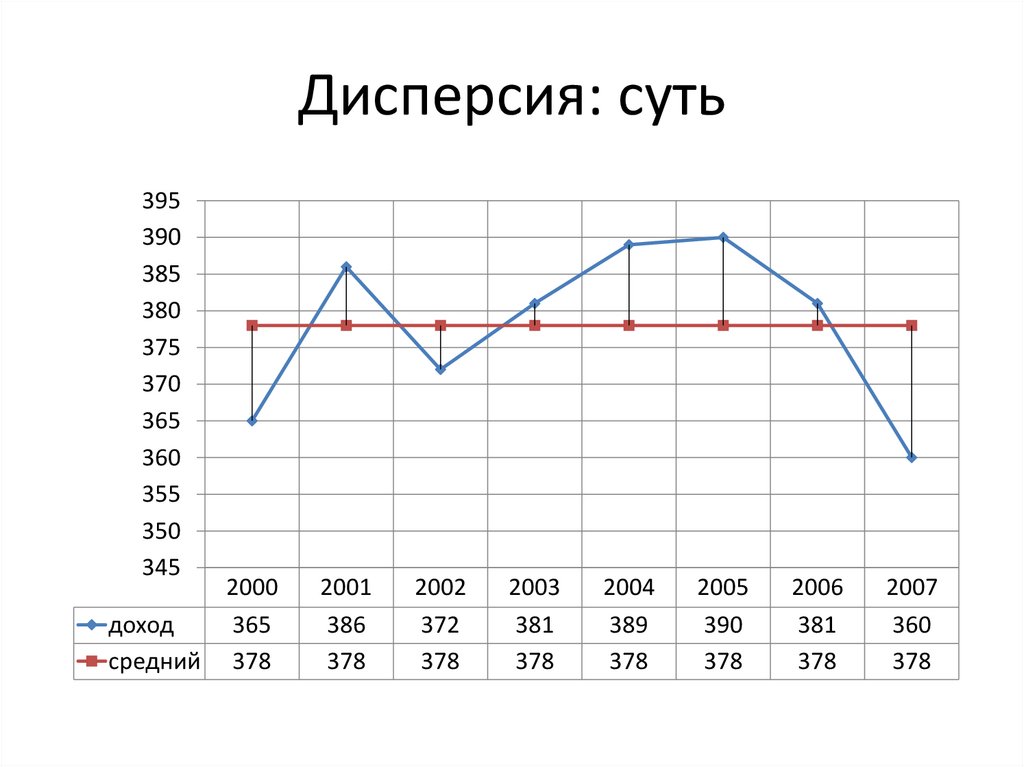
Дисперсия: суть395
390
385
380
375
370
365
360
355
350
345
2000
доход
365
средний 378
2001
386
378
2002
372
378
2003
381
378
2004
389
378
2005
390
378
2006
381
378
2007
360
378
18.
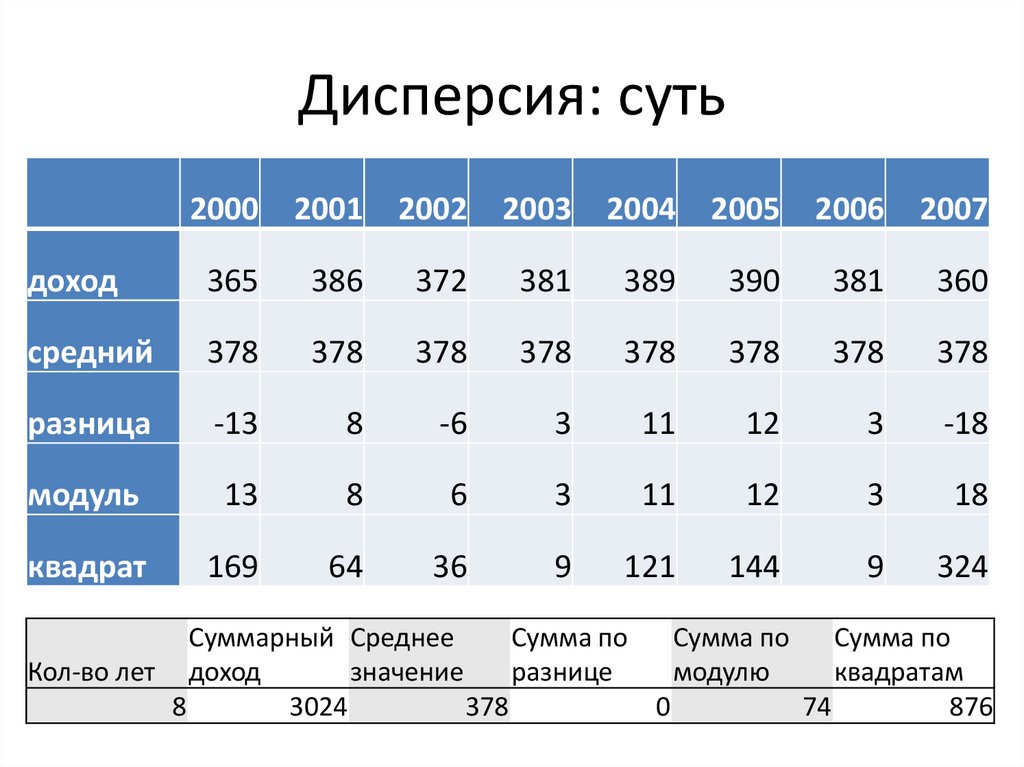
Дисперсия: суть2000
2001
2002
2003
2004
2005
2006
2007
доход
365
386
372
381
389
390
381
360
средний
378
378
378
378
378
378
378
378
разница
-13
8
-6
3
11
12
3
-18
модуль
13
8
6
3
11
12
3
18
квадрат
169
64
36
9
121
144
9
324
Суммарный Среднее
Сумма по
Сумма по
Сумма по
Кол-во лет доход
значение
разнице
модулю
квадратам
8
3024
378
0
74
876
19.
Вычисление ст. отклонения• Если кол-во случаев меньше 30, то делится
на кол-во значений за вычетом одного (n1);
• Если кол-во случаев больше 30, то делится
просто на кол-во значений (n);
• Для нашего случая: 11,2 (а не 10,5)
20.
Коэффициент вариации (V)• Отношение стандартного отклонения к
среднему (арифметическому) значению;
• Выражается в процентах;
• Для нашего дохода V=11,2/378=0,03 или 3%.
• Используется для сопоставления данных по
стандартному отклонению внутри подвыборок
и между собой;
21.
ОТКЛОНЕНИЕ ОТ НОРМАЛЬНОГОРАСПРЕДЕЛЕНИЯ
22.
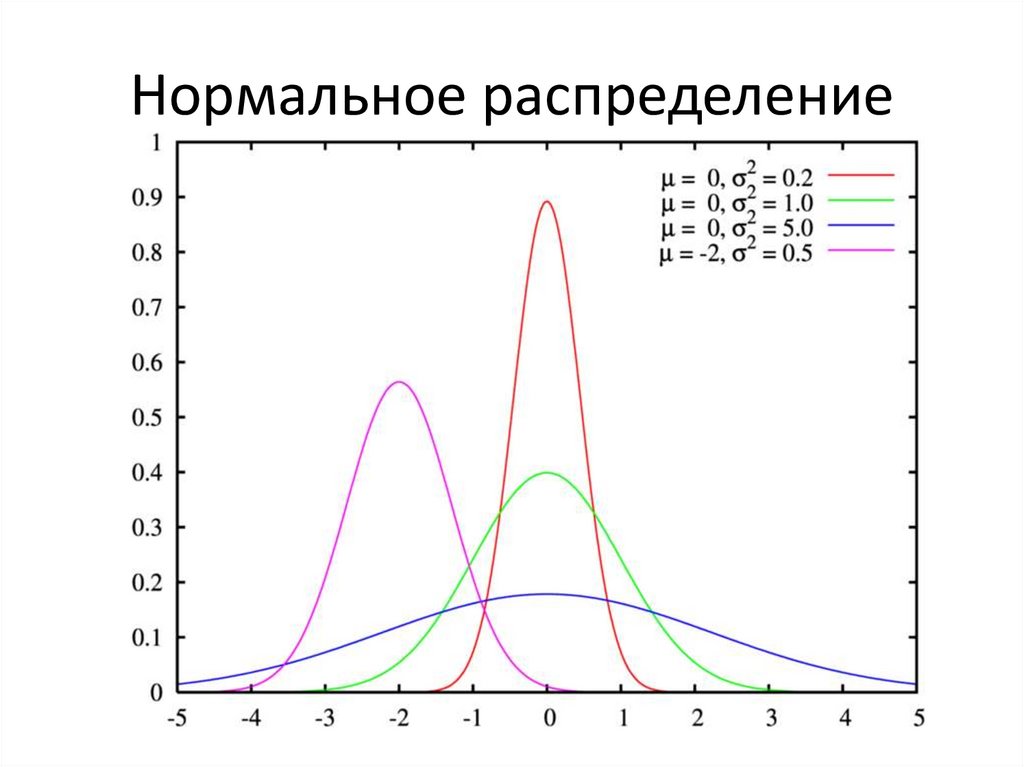
Нормально распределение• Как бы выглядел график, если бы
изучаемое явление подчинялось закону
распределения случайной величины
(специальная формула устанавливающая
отношение между средним, дисперсией,
медианой).
23.
Нормальное распределение24.
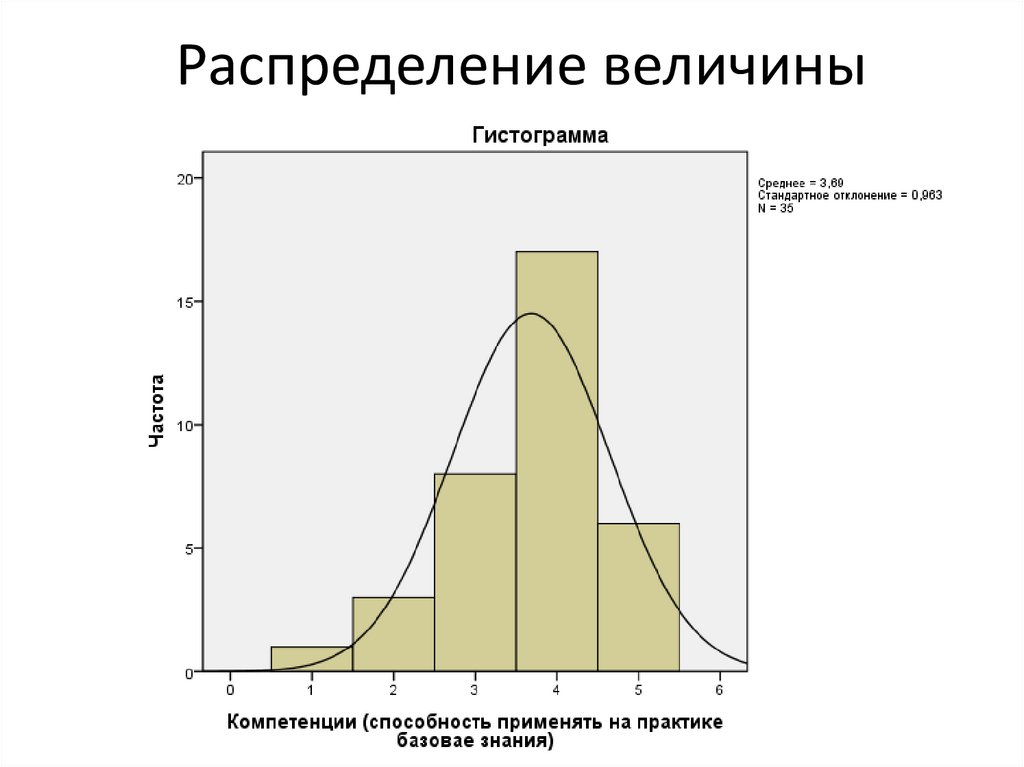
Распределение величины25.
Асимметрия• коэффициент, показывающий степень
отличия распределения случайной
величины от нормального ее
распределения;
= 3*(сред.арифм.–медиана)/станд.отклонение
• > 1 или < –1 означает скошенное
распределение;
26.
Правила:• Если форма симметричная, а асимметрия
меньше 1 по модулю – используйте
среднее значение, дисперсию и
стандартное отклонение;
• Если асимметрия значительна – моду,
медиану и квартили;
• коэффициент асимметрии положителен,
если правый хвост распределения длиннее
левого, и отрицателен в противном случае;
27.
Стандартное отклонение: правилооценок
Эмпирическое правило:
68% (2/3) значений – среднее +/- 1
станд.откл.
95% значений – среднее +/- 2 (1.96)
стандартных отклоненения
99% значение – среднее +/- 3
станд.отклонен.


















 mathematics
mathematics








