Similar presentations:
Парабола, линейная функция, вершина, дискриминант, ветви, ось симметрии, коэффициенты а, в, с
1.
Парабола, линейная функция,вершина, дискриминант, ветви,
ось симметрии, коэффициенты
а, в,. с.
2.
Составить математический рассказ натему «Квадратичная функция и её график»
• Парабола, вершина параболы,
дискриминант, ось симметрии,
коэффициенты а, в, с; нули функции,
наибольшее и наименьшее значение
функции, возрастание и убывание функции,
О.О.Ф и О.З.Ф., направление ветвей
параболы, пересечение параболы с осью
ОХ и ОУ, положительные и отрицательные
значения функции …
3.
4.
5.
Цель урока:1. повторение теоретического материала
по теме: «Свойства квадратичной
функции»
2. выяснить зависимость коэффициентов
a,b,c, m, n от расположения графика
квадратичной функции,
3. проверить навыки применять
теоретический материал для отыскания
коэффициентов.
6.
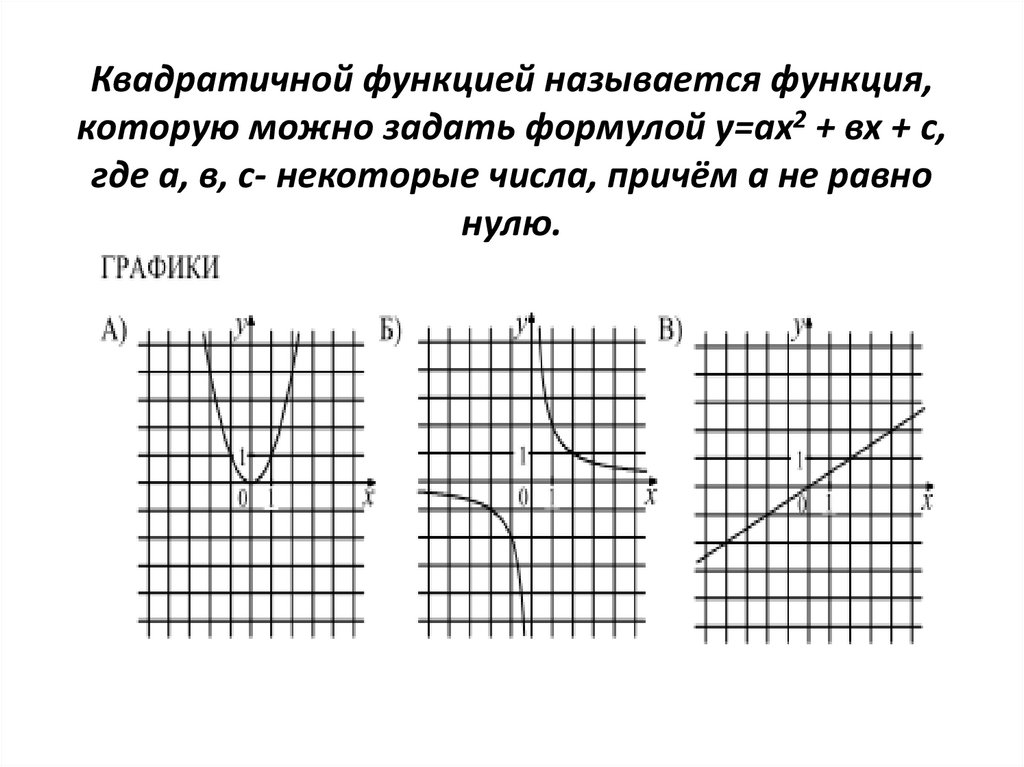
Квадратичной функцией называется функция,которую можно задать формулой у=ах2 + вх + с,
где а, в, с- некоторые числа, причём а не равно
нулю.
7.
.ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с
НА РАСПОЛОЖЕНИЕ
ГРАФИКА КВАДРАТИЧНОЙ
ФУНКЦИИ
8.
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НАРАСПОЛОЖЕНИЕ
ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
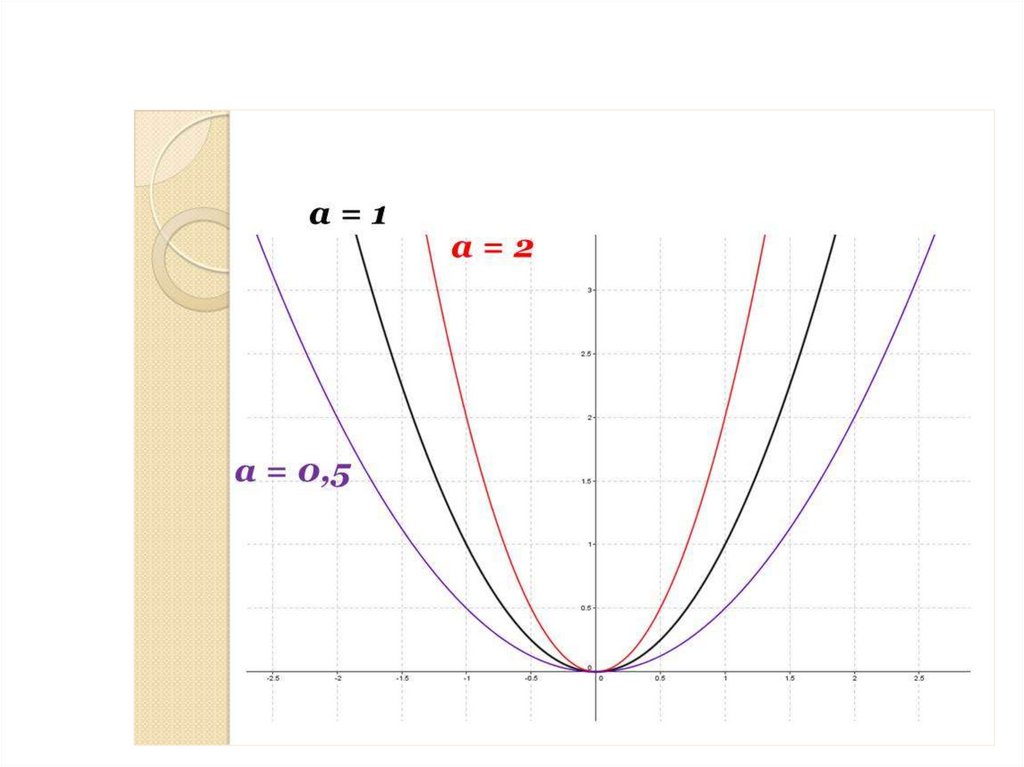
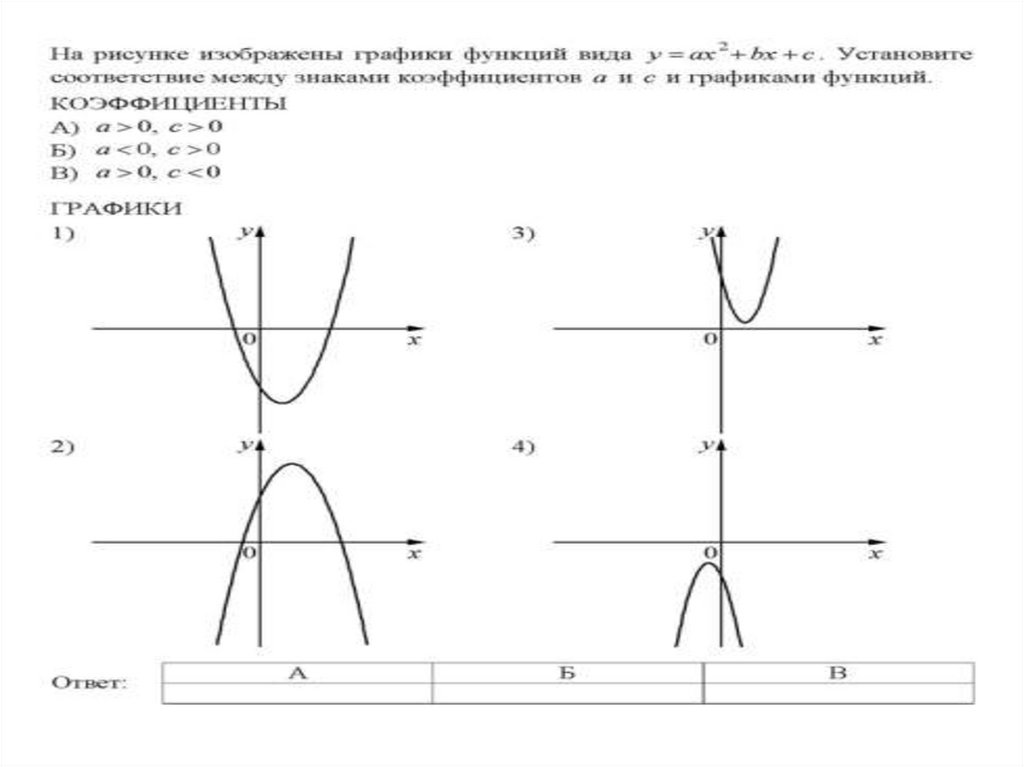
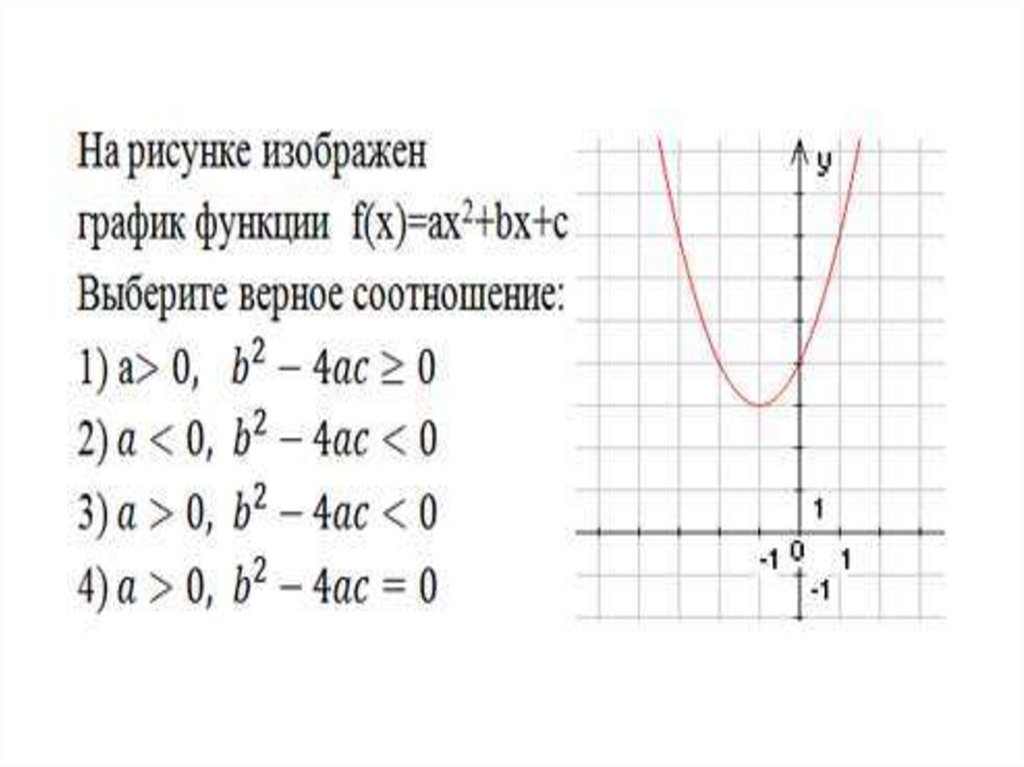
1) Коэффициент а влияет на направление
ветвей параболы:
при а > 0 – ветви направлены вверх,
при а < 0 – вниз.
2) Коэффициент b влияет на расположение
вершины параболы относительно оси ОУ.
При b = 0 вершина лежит на оси ОУ.
3) Коэффициент с показывает точку
пересечения параболы с осью ОУ.
9.
10.
11.
12.
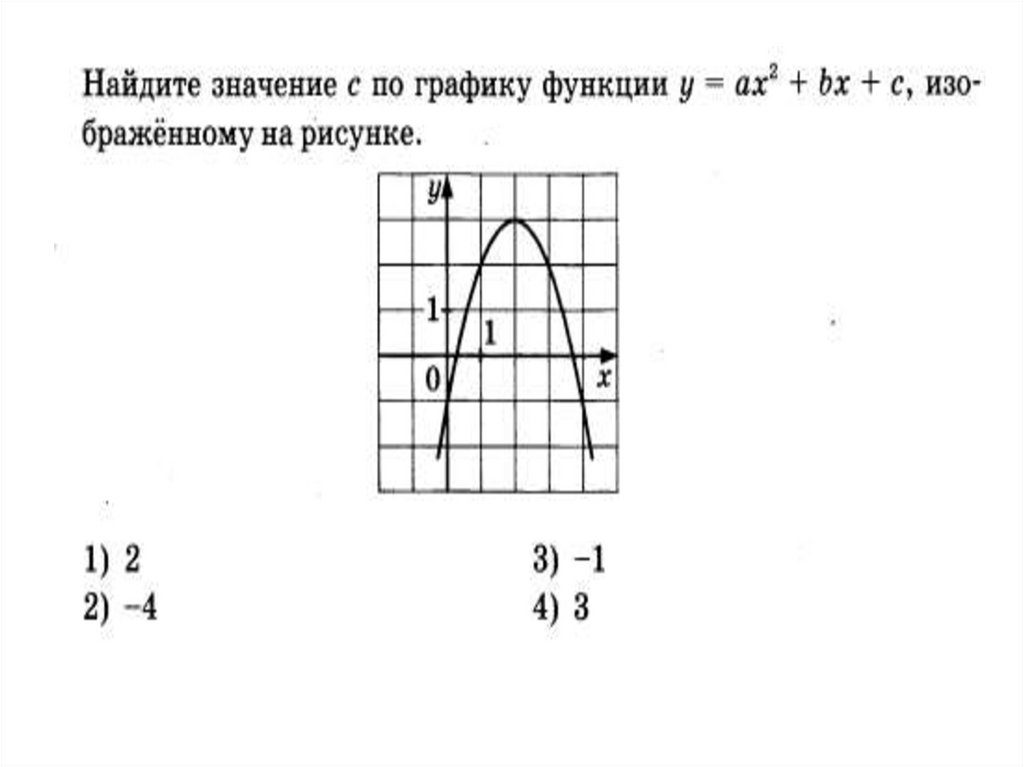
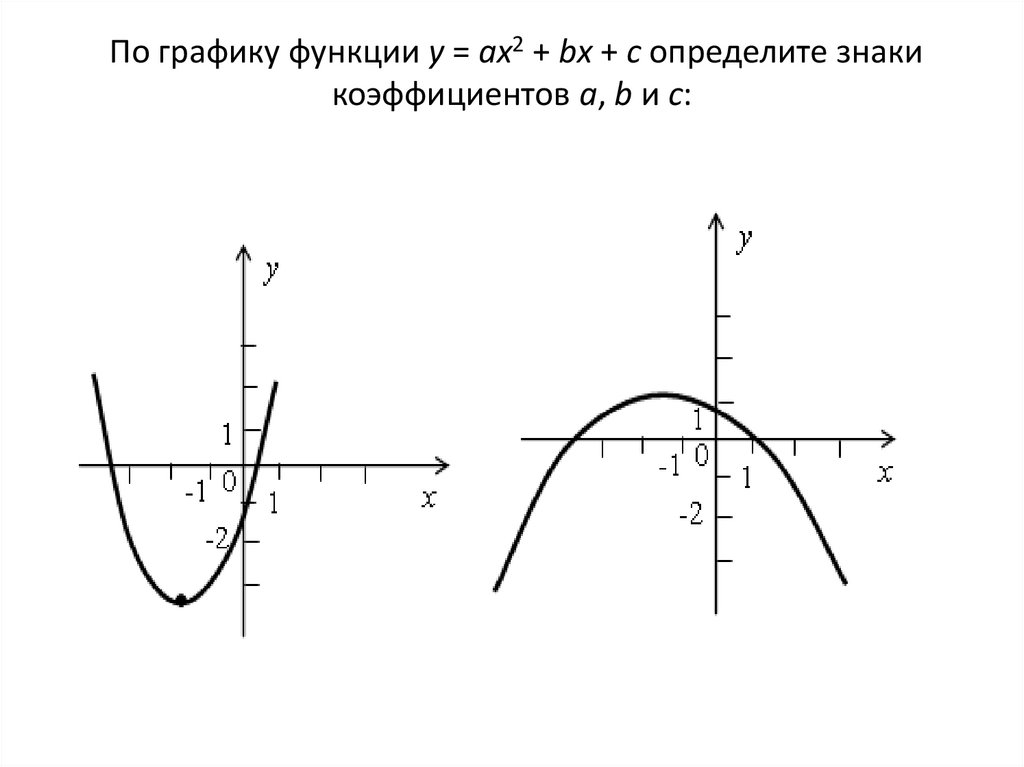
По графику функции у = ах2 + bх + с определите знакикоэффициентов а, b и с:
13.
14.
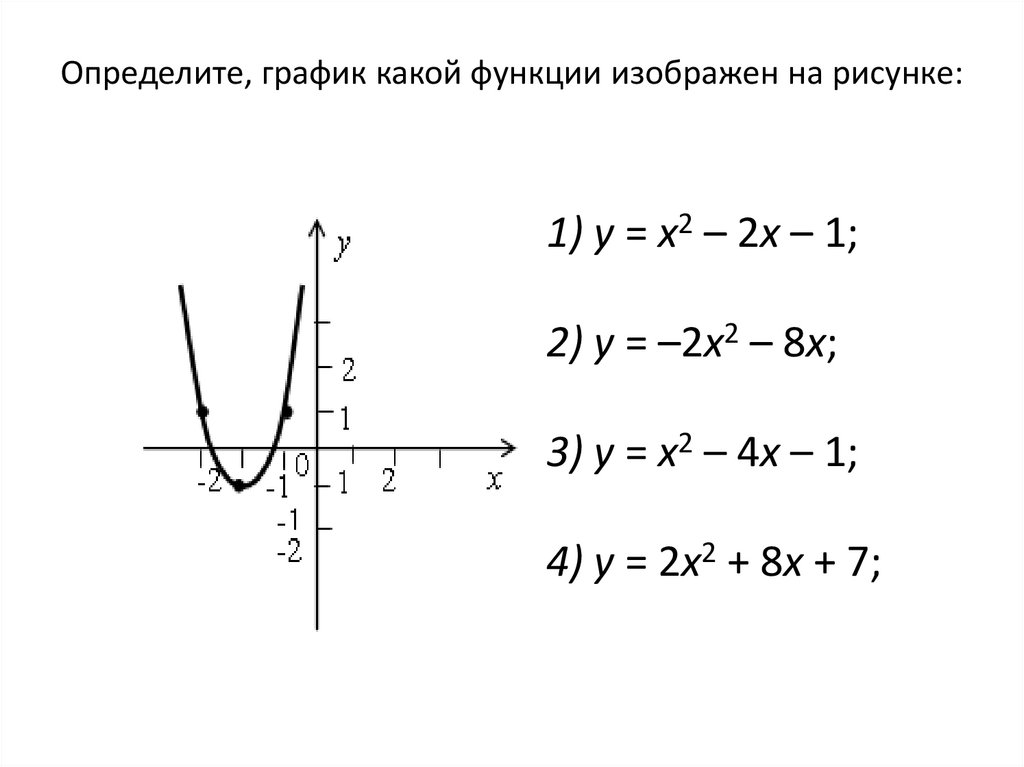
Определите, график какой функции изображен на рисунке:1) у = х2 – 2х – 1;
2) у = –2х2 – 8х;
3) у = х2 – 4х – 1;
4) у = 2х2 + 8х + 7;
15.
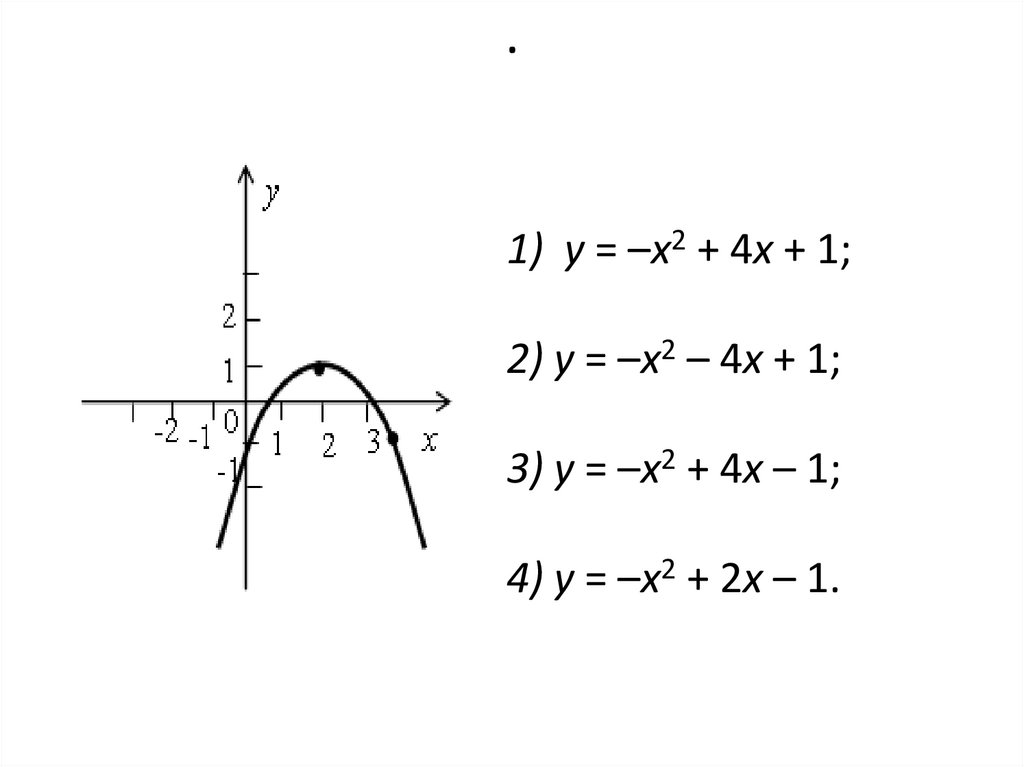
.1) у = –х2 + 4х + 1;
2) у = –х2 – 4х + 1;
3) у = –х2 + 4х – 1;
4) у = –х2 + 2х – 1.
16.
План построения графика квадратичной функции• 1) Определить направление ветвей параболы;
• 2) Вычислить координаты вершины параболы;
• 3) На координатной плоскости отметить вершину
параболы и направление ветви. Провести ось
симметрии параболы;
• 4) Заполнить таблицу для 2 – 3 точек, лежащих по
одну сторону от оси симметрии;
• 5) Полученные точки из таблицы нанести на
координатную плоскость и отметить им
симметричные точки относительно оси;
• 6) Точки соединить плавной линией. Парабола
17.
План решения задания:• ООФ
• Числитель разложить на множители
(биквадратное уравнение, теорема Виета)
• Выполнить сокращение, раскрытие скобок.
• Строим параболу с учётом ООФ («выколотые»
точки)
• Определяем, как выглядит прямая y = c
• Отвечаем на вопрос задачи
18.
Рефлексия.• Выбери утверждение, которое соответствует
тому, как тебе работалось на уроке.
1) Мне было всё понятно, я смог повторить
теоретический материал и могу решать задачи без
посторонней помощи.
2) Я вспомнил теоретический материал, решал задачи,
но некоторые задачи требуют посторонней
помощи.
3) Я плохо знаю теоретический материал, не смог его
вспомнить и не могу решать задачи по данной
теме.









 mathematics
mathematics








