Similar presentations:
Автоматика и управление
1.
Автоматика и управлениеТема 1. Основные понятия и
определения теории
автоматического управления
Цели и задачи дисциплины. Порядок изучения дисциплины. Рекомендуемая
литература, используемое программное обеспечение.
Лекция 1.1. Управление. Принципы управления САУ и САР: принцип обратной
связи, принцип управления по возмущению. Принципы построения САУ и САР.
Автоматическая система (АС). Элементы АС. Входные и выходные сигналы АС.
Алгоритмы функционирования элементов САУ и САР. Классификация САУ и САР.
Математический аппарат САУ и САР и их элементов: оператор ЛСС, задаваемый
линейным дифференциальным уравнением с постоянными коэффициентами.
Оператор постоянного запаздывания. Моделирование ЛСС на ЭВМ. Понятия об
оптимальных, самонастраивающихся и интеллектуальных СА
2.
Цель – формирование знаний общих принципов построения ирасчета систем автоматического управления в авиационной
технике, основ анализа и синтеза этих систем.
Обеспечивающие дисциплины: Б1.О.08 Высшая математика,
Б1.О.09 Информатика и информационные технологии, Б1.О.10
Физика, Б1.О.21 Электротехника, Б1.О.26 Основы электроники,
навыки Б2.В.01(У) Вычислительной практики
Обеспечиваемые дисциплины: Б1.В.04 Моделирование
авиационных систем и комплексов, Б1.О.20 Техническая
диагностика, Б1.В.09 Бортовые цифровые вычислительные
устройства, Б1.В.07 Системы электроснабжения воздушных судов,
Б1.В.08 Электрифицированное оборудование воздушных судов,
Б1.В.11 Системы автоматического управления полетом,
Б1.В.ДВ.01.01 Авиационные информационные измерительные
системы, Б1.В.ДВ.01.02 Приборные системы авионики,
Б1.В.ДВ.02.01 Пилотажно-навигационные комплексы,
Б1.В.ДВ.02.02 Авионика управления полетом, Б3.02(Д) Выпускная
квалификационная работа.
3.
В результате освоения дисциплины обучающийся должен:Знать: методы математического описания и исследования
элементов и систем регулирования и управления,
применяемые в авиационном оборудовании; инженерные
методы анализа автоматических систем различных классов;
методы синтеза различных классов автоматических систем;
методы исследования точности и динамических характеристик
авиационных систем с помощью ЭВМ.
Уметь: использовать классические методы исследования и
синтеза систем автоматического регулирования и управления
различных классов.
Владеть: методами оценки качества систем автоматического
регулирования и управления, оптимизации их параметров;
методами применения вычислительной техники при
проведении экспериментальных исследований автоматических
систем различных классов.
4.
Общий объем учебных часов надисциплину
Семестр
Объем аудиторной нагрузки
Лекции
Практические занятия
Лабораторные работы
Экзамен
Объем самостоятельной работы
студента
216 час.
4
94
32
42
20
36
сем.
час.
час.
час.
час.
час.
86
час.
(6 з.е.)
5.
Основная литература:• Лайков М.И. Автоматика и управление. Часть 1, Иркутск: МГТУ
ГА, 2010г., 305 с.
• Лайков М.И., Глухов В.В. Автоматика и управление. Часть II,
Иркутск: МГТУ ГА, 2011г., 267 с.
• Котлов Ю.В. Автоматика и управление: лабораторный практикум.
− Иркутск: Иркутский филиал МГТУ ГА, 2020. – 85 с.
Дополнительная литература
•Макаров, Е.Г. Mathcad: Учебный курс/ Е.Г. Макаров. - СПб: Питер,
2009. - 384 с.
•Дьяконов, В.П.VisSim+MathCad+MatLab. Визуальное
математическое моделирование / В.П. Дьяконов. – М.: Солон-Пресс,
2004.-383 с.
•Дьяконов, В.П. MATLAB. Полный самоучитель / В.П. Дьяконов.-М.:
ДМК Пресс, 2014.-768 с.
•Автоматика и телемеханика.
•Известия ВУЗ. Электроника.
•Научный вестник МГТУ ГА
6.
• Перечень ресурсов информационнотелекоммуникационной сети «Интернет»,необходимых для освоения учебной дисциплины
•«www.if_mstuca.ru» в разделах «библиотека»,
«электронные УМК».
•http://www.mstuca.ru/ - официальный сайт МГТУ ГА;
•http://bd.viniti.ru/ - База научно-технической информации
ВИНИТИ РАН.
•http://www.e.lanbook.com/ - ЭБС издательства «Лань»;
•http://www.biblio-online.ru/ - библиотечная система.
Программное обеспечение
1.Vissim.
2.Mathcad 15.
3.MatLab.
7.
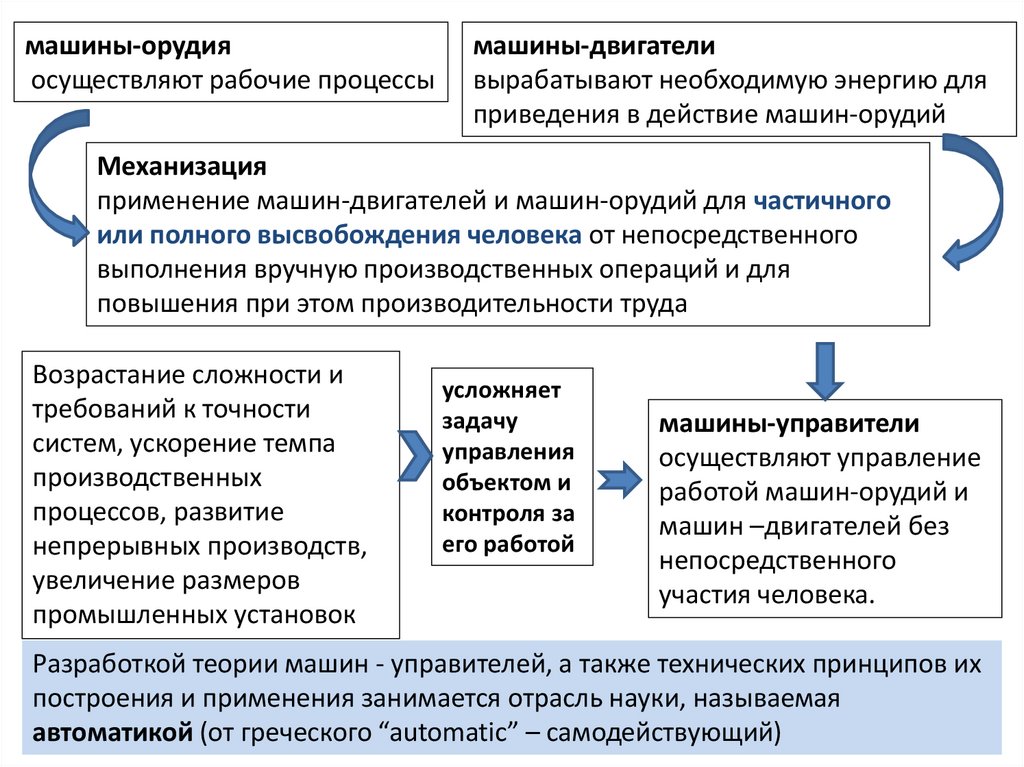
машины-орудияосуществляют рабочие процессы
машины-двигатели
вырабатывают необходимую энергию для
приведения в действие машин-орудий
Механизация
применение машин-двигателей и машин-орудий для частичного
или полного высвобождения человека от непосредственного
выполнения вручную производственных операций и для
повышения при этом производительности труда
Возрастание сложности и
требований к точности
систем, ускорение темпа
производственных
процессов, развитие
непрерывных производств,
увеличение размеров
промышленных установок
усложняет
задачу
управления
объектом и
контроля за
его работой
машины-управители
осуществляют управление
работой машин-орудий и
машин –двигателей без
непосредственного
участия человека.
Разработкой теории машин - управителей, а также технических принципов их
построения и применения занимается отрасль науки, называемая
автоматикой (от греческого “automatic” – самодействующий)
8.
Первые промышленные автоматические устройстваПоплавковый регулятор уровня воды в
паровой машине (1765 г. И.И.Ползунов)
Автоматический суппорт А.Нортова для
токарно-копировального станка
(Россия)
Центробежный регулятор Уатта
(Англия)
Ткацкий станок с программным
управлением Ж.Жаккара (Франция)
Основоположники автоматики:
П.А.Чебышев – первый труд “О регуляторах” (1838 г.),
К.Э.Циолковский, И.А.Вышнеградский, Б.С.Якоби,
А.М.Ляпунов, А.Н. Колмогоров, Максвел, Найквист,
А.Стодола, Гольдфарб, Гурвиц, Винер и др.
9.
Этапы развития автоматикиI этап – инженерный. Завершенные формы принял к
середине XX столетия. Предметом данного этапа
являются инженерные методы решения задач
автоматики, которые впервые были изложены в виде
курса лекций в работе профессора Н.Е.Жуковского
“Теория регулирования хода машин” (1909 г.).
II этап – современная автоматика или ТАУ.
Значительный вклад в развитие автоматики внесли: В
России А.М. Ляпунов, Я.З. Цыпкин, Л.С. Понтрягин, А.М.
Летов, С.П. Королев, Д.А. Поспелов, А.А. Красовский,
В.Н.Буков и др.,
за рубежом – Норберт Винер, Р. Белман, П.Эйкхофф, Р.
Калман и др.
10.
Процессы управления и обработки информации всистемах любой природы изучает наука кибернетика.
Один из ее разделов, связанный главным образом с
техническими системами, называется теорией
автоматического управления.
Кроме классических задач регулирования, она
занимается также оптимизацией законов управления,
вопросами приспособляемости (адаптации).
Иногда названия «теория автоматического управления»
и «теория автоматического регулирования»
используются как синонимы.
В современной зарубежной литературе – control theory.
11.
1.1. Управление. Принципы управления САУ и САР:принцип обратной связи, принцип управления по
возмущению
Управлением называется любое целенаправленное
воздействие на объект управления, (ЛА, АД,
электрическая машина, гироплатформа и т.д.),
предназначенное для изменения процессов в желаемом
направлении.
В общем случае (но не всегда) в управлении можно
выделить 4 составляющих:
- получение информации о задаче управления;
- получение информации о результате управления;
- выработка сигнала управления на основе анализа
информации о задаче и результате управления;
- целенаправленное воздействие на объект управления
выработанным сигналом управления.
12.
Управление может осуществляться по двум принципам:1. Принцип обратной связи – использование в
процессе
управления
информации
о
результате
управления. В этом случае сигнал управления
формируется исходя из информации о задаче управления
и текущем состоянии объекта управления (ОУ). Поэтому,
управление по принципу обратной связи называют
управлением по замкнутому циклу. Это основной
принцип управления в авиационной автоматике.
2. Принцип управления по возмущению информация о результате управления по какой либо
причине не используется в процессе управления. Поэтому
такой принцип управления называют управлением по
разомкнутому циклу.
13.
Системы автоматики, в зависимости от выполняемых функций,делятся на автоматические системы контроля и
автоматические системы регулирования (или управления).
Последние в свою очередь могут быть замкнутыми или
разомкнутыми.
Автоматическая система контроля (АСК) осуществляет
сравнение контролируемой величины с заданным (эталонным)
значением и фиксирование результатов сравнения в форме,
удобной для наблюдения и длительного хранения.
ЗУ
КО
Д
СУ
ВУ
КО – контролируемый объект; Д – датчик;
СУ – сравнивающее устройство; ЗУ – задающее устройство;
ВУ – воспроизводящее устройство.
14.
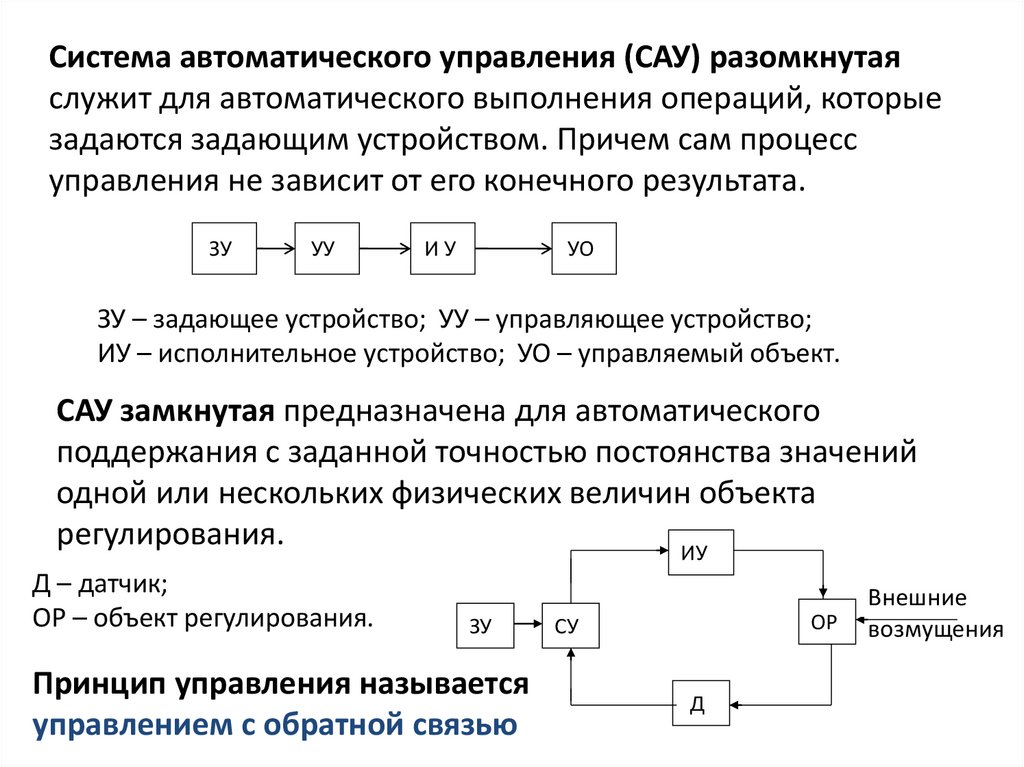
Система автоматического управления (САУ) разомкнутаяслужит для автоматического выполнения операций, которые
задаются задающим устройством. Причем сам процесс
управления не зависит от его конечного результата.
ЗУ
УУ
ИУ
УО
ЗУ – задающее устройство; УУ – управляющее устройство;
ИУ – исполнительное устройство; УО – управляемый объект.
САУ замкнутая предназначена для автоматического
поддержания с заданной точностью постоянства значений
одной или нескольких физических величин объекта
регулирования.
ИУ
Д – датчик;
ОР – объект регулирования.
ЗУ
Принцип управления называется
управлением с обратной связью
ОР
СУ
Д
Внешние
возмущения
15.
В зависимости от характера изменения во временизаданного значения регулируемого параметра замкнутые
системы автоматического регулирования делятся на:
системы стабилизации,
следящие системы,
системы программного регулирования.
Системы автоматической стабилизации предназначены для
поддержания регулируемой величины у на заданном уровне. В
этих системах входная величина x = const.
В следящих системах входная величина (заданное значение
регулируемого параметра) изменяется по произвольному или,
точнее, случайному закону во времени: x = x(t). Если
рассогласование ε = x – y ≈ 0, то выходная (регулируемая)
величина системы повторяет закон изменения входной
величины – “следит” за ее изменениями: y(t) ≈ x(t).
16.
В автоматических системах программного регулированияобеспечивается изменение регулируемой величины по
определенной программе. В этом случае x = x(t) является
программно изменяющейся величиной, при ε→ 0, y ≈ x(t)
Разомкнутые системы подразделяются на системы
компенсации и разомкнутые системы программного
управления.
Системы компенсации предназначены для уменьшения
влияния возмущающих воздействий на управляемый процесс
или объект путем измерения этих воздействий и
компенсации их влияния за счет дополнительного
воздействия на объект. Рабочей информацией в системах
компенсации является возмущающее воздействие.
Разомкнутые системы программного управления выполняют
заданную последовательность действий, не зависящих от
получаемого результата (например, автомат запуска
авиационного двигателя)
17.
Дальнейшее развитие автоматики привело ксозданию самонастраивающихся систем, которые
в определенной степени могут приспосабливаться к
изменяющимся внешним условиям.
К таким системам относится специфический класс
экстремальных систем (оптимальных систем,
или оптимизаторов), которые настраивают
управляемый процесс на оптимальное значение
какого-либо показателя процесса (например,
минимума расхода топлива двигателем).
18.
1.2. Принцип построения САУ и САР.Автоматическая система (АС). Элементы АС
Совокупность элементов, обеспечивающих управление,
называется управляющим устройством (УУ).
Простые УУ называются регуляторами, сложные – системами
автоматического управления (САУ)
Если управление с помощью вышеперечисленных устройств
осуществляется без участия человека – оператора, то
такое управляющее устройство называется
автоматическим (АУУ)
Для исследования процессов управления необходимо объект
управления (ОУ) и УУ рассматривать как единую
динамическую систему.
Совокупность АУУ и ОУ, рассматриваемых как единое
целое, называется автоматической системой (АС)
19.
Для построения АС функционально необходимыследующие основные элементы:
1) Источники информации о задаче и результате
управления – измерители физических величин
(датчики);
2) Устройство обработки информации –
вычислители (аналоговые или цифровые);
3) Исполнительное устройство – совокупность
технических средств, позволяющих перейти от сигнала
управления к непосредственному управлению объектом
(преобразователи, усилители, двигатели);
4) Линии связи (электрические, механические,
гидравлические, оптические и т.д.).
Для обеспечения необходимого качества работы АС
используются также
5) Корректирующие устройства (R-C-цепочки,
тахогенераторы и т.д.)
20.
21.
Систему S можно представить в виде множества величин,описывающих процесс функционирования реальной системы
и образующих следующие подмножества:
•подмножество входных воздействий: xi X , i 1,2,..., nX
x x1 , x2 ,..., xn X );
•подмножество воздействий внешней среды: vl V , l 1,2,..., nV
(или вектор входящих воздействий
(или вектор воздействия внешней среды v v1 , v2 ,..., vn
V
• подмножество собственных параметров
hk H , k 1,2,..., nH
системы:
(или вектор внутренних параметров h h1 , h2 ,..., hnH );
•подмножество выходных характеристик системы:
);
y j Y , j 1,2,..., nY
y y1 , y2 ,..., yn ).
(или вектор выходных характеристик
Y
зависимым (эндогенным) независимыми (экзогенными)
1.3. Входные и выходные сигналы АС. Пространство
состояния
22.
Процесс функционирования системы описывается во времениоператором Fs, который преобразует экзогенные переменные в
эндогенные в соответствии с соотношением
y (t ) Fs ( x, v, h, t )
Эта зависимость называется законом функционирования
системы S.
Закон функционирования Fs может быть задан в виде функции,
функционала, логических условий, алгоритмически или
таблично, а также в виде словесного набора правил
соответствия.
Совокупность зависимостей выходных характеристик системы от
времени называется выходной траекторией y(t).
23.
Закон функционирования y (t ) Fs ( x, v, h, t ) являетсяматематическим описанием поведения системы во времени, т.е.
модели такого типа относятся к динамическими моделям.
Если закон функционирования не содержит параметра времени, то
такие модели называются статическими и отображают связь между
подмножеством у и подмножествами x,v,h и записывается как
y Fs ( x, v, h)
Если в динамической модели дискретизировать время, то в каждый
момент времени можно определить состояние системы
z p Z , p 1,2,..., nZ . Множество Z всех возможных состояний
системы называется пространством состояний системы. Процесс
функционирования системы, изменяющей свое состояние в
фиксированные моменты времени, можно описать векторными
уравнениями:
Переходное отображение
Отображение выхода
0
z (t ) Фs ( z , x, v, h, t )
y (t ) Fs ( z, t )
24.
Задачей любого управления является целенаправленноеизменение текущего динамического состояния ОУ.
Текущее динамическое состояние ОУ характеризуется
определенным числом физических величин, называемых
координатами состояния или фазовыми координатами.
Полная совокупность физических величин (координат
состояния), характеризующая динамическое состояние
ОУ называется пространством состояния (фазовым
пространством)
В процессе управления целенаправленному изменению подлежат, как
правило, не все координаты состояния, а лишь часть из них.
Координаты состояния ОУ, подлежащие
целенаправленному изменению в процессе управления и
характеризующие результат управления называются
выходными сигналами АС (регулируемыми координатами
состояния, регулируемыми параметрами)
25.
Число выходных сигналов АС может быть:- один – в дальнейшем будем обозначать его y(t) (пример: система
стабилизации постоянного напряжения);
- два и более y1(t), y2(t), …, yn(t).
Выходные сигналы АС – реальные физические величины,
которые могут быть измерены датчиками.
Выходные
сигналы,
изменяющиеся
по
законам,
обусловленным целью управления, называются желаемыми
выходными сигналами – yж(t).
Пример: Система стабилизации углового положения самолета
имеет три выходных сигнала, т.к. положение самолета в пространстве
характеризуется тремя углами: , ,ψ, т.е. y1(t) = (t); y2(t) = (t);
y3(t)=ψ(t). Тогда пространство состояний ОУ можно записать в
векторной форме:
(t )
y (t ) y 2 (t ) (t )
y3 (t ) (t )
y1 (t )
или
T
y (t ) y1 (t ) y2 (t) y3 (t) .
26.
Все внешние по отношению к АС воздействия,вызывающие изменение выходных сигналов,
называются входными сигналами АС.
Входные сигналы разделяются на:
•Задающие воздействия (полезный сигнал) xi(t) –
входные сигналы, которые содержат информацию о
задаче управления и определяют желаемые выходные
сигналы;
•Возмущения или помехи (вредные входные сигналы)
fj(t) – не содержат информацию о задаче управления, а
лишь искажают работу АС.
27.
1.4. Алгоритмы функционирования АС (САУ) –оператор, математическая модель АС
Рассмотрим АС с входными сигналами x(t), f(t),…,fm(t) и выходным
сигналом y(t):
x(t)
y(t)
f1(t)
fm(t)
АС
Н.У.
x(t) –задающее воздействие; f1(t),…, fm(t) – возмущения
Выходной сигнал y(t) зависит от всех входных сигналов, свойств
самой АС и её начального состояния (Н.У.).
Правило, устанавливающее связь между любой заданной
совокупностью входных сигналов x(t), f(t),…,fm(t) и выходным
сигналом y(t) называется оператором АС и записывается в виде:
Y(t) = A[x(t), f(t),…,fm(t)]
28.
Представлениеоператора
математическим
выражением называется математической моделью
АС.
Характеристики,
позволяющие
определить
математическое выражение оператора (матмодель)
называются динамическими характеристиками АС.
29.
Примеры операторов (виды):•Операторы, задаваемые
дифференциальными
уравнениями (ДУ) с заданными
начальными условиями (НУ):
an(t)y(n)+…+ a1(t)y(1)(t) + ao(t)y(t) =
вm(t)x(m)+ вo(t)x(t),
при t = to, yo = y(to), …, [yo(n-1)= y(n1)(t )]
о
зависимость y(t) в любой текущий
момент времени t от всех значений
х(t) на отрезке от tо до t
Функциональные операторы.
1.y(t) = K x(t);
2.y(t) = K Sin x(t);
3.y(t) = K x2(t);
где К – некоторые константы.
Зависимость y(t) от значения x(t) в
тот
же
момент
времени
(независимость от значений x(t) в
предыдущие
и
последующие
моменты времени)
t
Интегральные операторы
y (t ) k g (t , ) x( )d ( ),
to
Где g (t , ) - некоторая заданная функция, а k – некоторая константа.
Общие свойства: y(t) зависит от всех значений x(t) на отрезке времени от
tо до t.
Операторы постоянного запаздывания
y(t) = K x(t–τ)
где К и τ некоторые вещественные константы
Общие свойства: y(t) в любой текущий момент времени t зависит
от одного предшествующего значения х в момент времени t–τ
30.
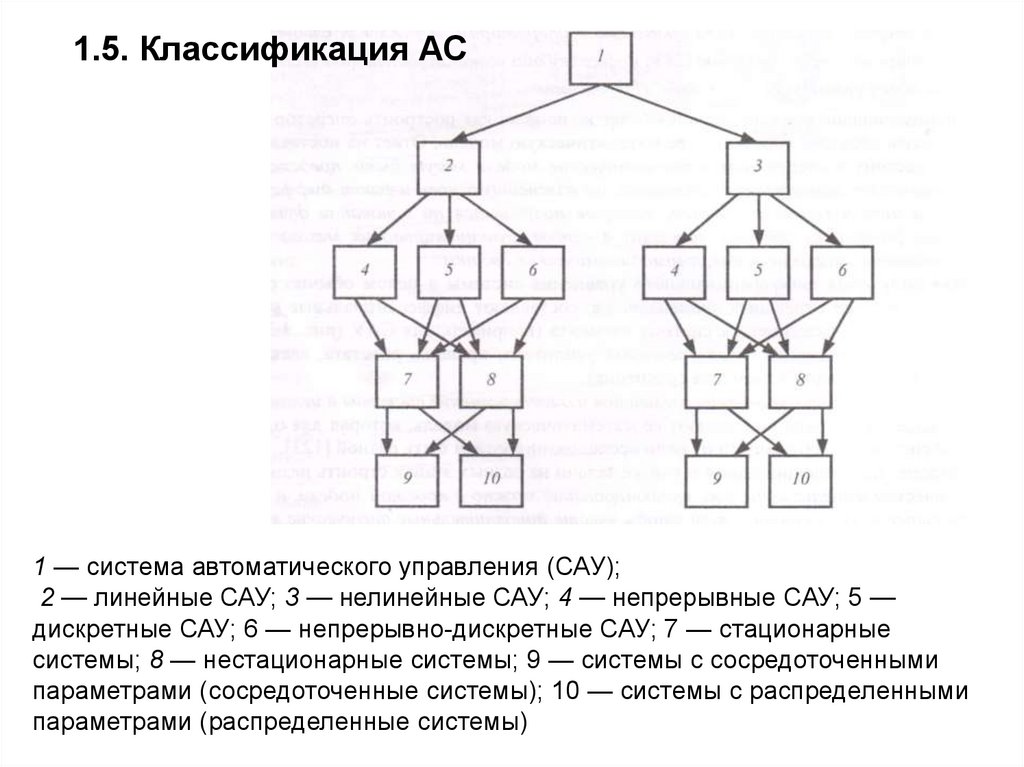
1.5. Классификация АС1 — система автоматического управления (САУ);
2 — линейные САУ; 3 — нелинейные САУ; 4 — непрерывные САУ; 5 —
дискретные САУ; 6 — непрерывно-дискретные САУ; 7 — стационарные
системы; 8 — нестационарные системы; 9 — системы с сосредоточенными
параметрами (сосредоточенные системы); 10 — системы с распределенными
параметрами (распределенные системы)
31.
Линейные и нелинейные АСАС называется линейной, если её оператор
y(t) = A[x(t)]
(1)
удовлетворяет принципу суперпозиции, который
определяется равенством:
A[C1x1(t) + C2x2(t)] = C1A[x1(t)] + C2 A[x2(t)].
(2)
где x1(t), x2(t) – любые входные сигналы, С1, С2 –
любые вещественные константы.
Из (2) следует, что для линейных АС её реакция
y(t) = A[C1x1(t) + C2x2(t)] = C1y1(t) + C2y2(t)
на любую линейную комбинацию сигналов x1(t) и x2(t)
равна такой же линейной комбинации реакций системы
на каждый сигнал в отдельности, т.е. y1(t) = A[x1(t)] и y2(t) =
A[x2(t)]
32.
Свойства линейных АС:1. С1 = С2 = 1.
Тогда A[x1(t) + x2(t)] = A[x1(t)] + A[x2(t)] = y1(t) + y2(t)
Реакция линейной АС на сумму сигналов равна сумме
реакций АС на каждый сигнал в отдельности
2. A[Cx(t)] = CA[x(t)] = Cy(t)
При изменении входного сигнала в С раз, выходной
сигнал линейной АС также изменится в С раз
3. A[-x(t)] = - A[x(t)] = -y(t)
При изменении знака входного сигнала, изменяется
знак выходного сигнала линейной АС
4. A[0] ≡ 0
Реакция линейной АС на нулевой входной сигнал
тождественно равна 0
33.
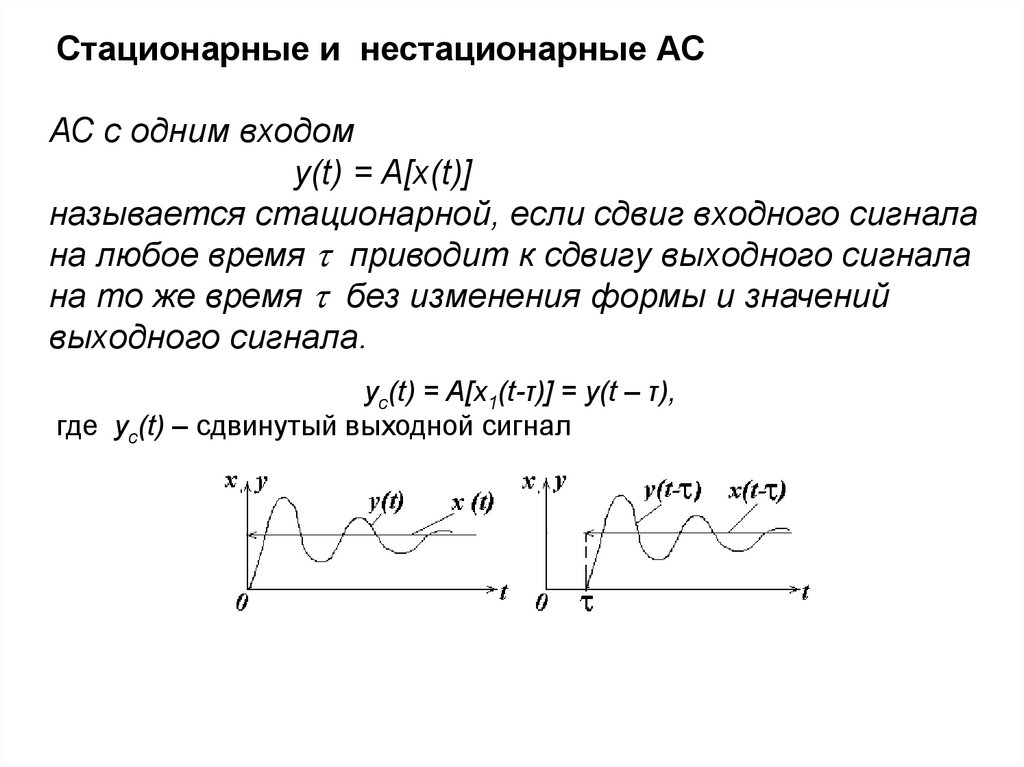
Стационарные и нестационарные АСАС с одним входом
y(t) = A[x(t)]
называется стационарной, если сдвиг входного сигнала
на любое время приводит к сдвигу выходного сигнала
на то же время без изменения формы и значений
выходного сигнала.
yс(t) = A[x1(t-τ)] = y(t – τ),
где yс(t) – сдвинутый выходной сигнал
34.
Для нестационарных АС характерным являетсяследующее свойство: выходной сигнал системы
зависит от времени подачи входного сигнала.
Нестационарными системами (линейными или
нелинейными) называют системы автоматического
управления, поведение которых описывается
дифференциальными уравнениями или системами
уравнений с переменными коэффициентами.
an(t)y(n)+…+ a1(t) y(1)(t) + ao(t) y(t) = вm(t)x(m)+ вo(t)x(t),
35.
Стационарными являются операторы:•y(t) = K x(t);
•ЛДУ с постоянными коэффициентами;
• y(i)(t) = К x(i)(t-τ)
•Интегральные операторы вида:
t
y (t ) g (t ) x( )d
t0
Нестационарными являются операторы:
•y(t) = K(t)x(t);
•ЛДУ с переменными коэффициентами
n
m
(i )
a
(
t
)
y
(
t
)
в
(
t
)
x
(t ),
i
i
(i )
i 0
i 0
•Интегральные операторы вида:
t
y (t ) g (t , ) x( )d
t0
36.
Сосредоточенными, или системами ссосредоточенными параметрами, называются
системы, поведение которых описывается
обыкновенными дифференциальными уравнениями.
Распределенные системы — это системы, которые
описываются дифференциальными уравнениями в
частных производных.
Если неизвестная функция является функцией одной переменной,
то дифференциальное уравнение называют обыкновенным
(сокращенно ОДУ – обыкновенное дифференциальное уравнение)
Если же неизвестная функция есть функция многих переменных,
то дифференциальное уравнение называют уравнением в
частных производных.
37.
Одномерные и многомерные АСОдномерной называется АС с одним выходным сигналом
y(t) = A[x(t), f1(t),…fm(t)]
Многомерной называется АС у которой число управляемых
координат (выходных сигналов) два и более
y( t ) A x( t ), F( t ) ,
y (t ) - вектор выходных сигналов размерностью (n 1)
х(t ) - вектор входных (задающих) сигналов размерностью (m 1)
F (t ) - вектор возмущений (помех) – (k 1)
38.
Непрерывные и дискретные АСНепрерывной называется АС, в которой циркулируют
непрерывные во времени входные и выходные сигналы, а связь
между элементами АС постоянна.
Дискретной называется АС, в которой периодически прерываются
одна или несколько связей между её элементами, приводящие к
появлению в системе прерывистых (импульсных) сигналов.
Поэтому иногда такие системы называют импульсными.
Оператор дискретной АС можно записать в виде:
yi A xi
где yi, xi – значения выходного и входного сигналов в моменты
прерывания связей между элементами – ti
ti = T·i,
T – период дискретности, i 0,
- номер дискрета
39.
Детерминированные и стохастические АСДетерминированной называется АС, которая
находится под воздействием неслучайных (известных
во времени, детерминированных) входных сигналов.
Стохастической называется АС находящаяся под
воздействием случайных (непредсказуемых заранее
функций времени) входных сигналов.
Раздел ТАУ, посвященный исследованию
стохастических АС, называется статистической
динамикой.
40.
1.6. Математический аппарат САУ и САР:оператор линейной стационарной системы ЛСС, задаваемый
линейным дифференциальным
уравнением с постоянными коэффициентами, две формы
его представления.
Первая форма
an y(n)(t)+..+a1 y(1)(t)+a0 y(t)=bm x(m)(t)+..+b1 x(1)(t)+b0 x(t)
(1)
где x(t), y(t) - входной и выходной сигналы АС, соответственно;
ai,(i=0,1,2,...,n);
bi,(i=0,1,2,...,m)
заданные
вещественные
коэффициенты, называемые параметрами АС
Порядок n старшей производной выходного сигнала (порядок
л.д.у.) называется порядком АС.
Для технически реализуемых систем с оператором (1)
справедливо условие:
m≤n
(2)
называемое условием технической реализуемости АС.
41.
Рассмотрим систему aoy(t)=b1x(1)(t)или
dx(t )
y (t ) K
dt
n = 0, m = 1
b1
K
ao
Пусть x(t) = Aх Sin t. Тогда y(t) = KAх Cos t, где KAх = Aу .
Коэффициент усиления по амплитуде идеального
дифференциатора будет
Ay
Ax
K
и при бесконечном увеличении частоты входного сигнала он
должен неограниченно возрастать, что технически невозможно.
42.
Чтобы определить выходной сигнал y(t) по заданному входномусигналу x(t), необходимо:
• Вычислить правую часть оператора, продифференцировав x(t)
m раз.
• Решить л.д.у. при нулевых начальных условиях.
Проблема ! Продифференцировать x(t) m раз возможно только
для гладких функций x(t), т.е. имеющих m производных.
Реальные входные сигналы могут быть вообще не
дифференцируемы или иметь ограниченную производную
меньше m.
x
t
0
Неправомерность для не дифференцируемых m раз входных
сигналов - недостаток первой формы
43.
Вторая форма - это два уравнения следующего вида:an u(n)(t)+...+a1 u(1)(t)+a0 u(t) = x(t),
y(t) = bm u(m)(t)+...+b1 u(1)(t)+b0 u(t),
где u(t) - вспомогательная переменная, дифференцируемая n раз.
В уравнениях отсутствуют производные от входного сигнала x(t), что
было недостатком первой формы
Для АС с оператором второй формы, чтобы определить y(t) по
заданному x(t), необходимо:
1. Решить первое л.д.у. при нулевых начальных условиях. Это
решение не накладывает никаких ограничений на вид x(t). В
результате решения уравнения определяется функция u(t).
2. Определить y(t) решением второго функционального
уравнения, которое, для технически реализуемых систем, всегда
имеет смысл, так как m < n.
44.
1.7 Оператор постоянного запаздыванияЛинейным стационарным является оператор
постоянного запаздывания:
y(t) = K x(t- ),
где К - вещественный коэффициент,
- вещественная константа с размерностью
времени, называемая временем запаздывания.
Все виды линейных стационарных систем могут
быть описаны двумя видами операторов:
- л.д.у. с постоянными коэффициентами и нулевыми
начальными условиями,
- оператором постоянного запаздывания.
45.
1.8. Моделирование ЛСС на вычислительныхмашинах.
Используется вторая форма описания оператора ЛСС:
an u(n)(t)+...+a1 u(1)(t)+a0 u(t) = x(t),
(1)
y(t) = bm u(m)(t)+...+b1 u(1)(t)+b0 u(t).
(2)
необходимо привести его к форме Коши - эквивалентной системе из
n-дифференциальных уравнений первого порядка.
1. Вводится n вспомогательных переменных
u1(t) = u(t),
u2(t) = u1(1)(t) = u(1)(t),
u3(t) = u2(1)(t) = u(2)(t),
..............................................
un(t) = un( 1 )1 (t) = u(n-1)(t).
(3)
46.
2. Дифференциальное уравнение (1)записывается с учетом (3):
an u(n)(t)+...+a1 u(1)(t)+a0 u(t) = x(t), (1)
an 1
a0
1
(1)
u
(
t
)
u
(
t
)
u
(
t
)
x(t ),
n 1
1
n 1
an
an
an
u1(t) = u(t),
(1)
u1 (t ) u2 (t ),
u2(t) = u1(1)(t) = u(1)(t),
(1)
u3(t) = u2(1)(t) = u(2)(t),
(3)
(4)
u
(
t
)
u
(
t
)
2
3
..............................................
un(t) = u n( 1 )1 (t) = u(n-1)(t).
un(1 )1 (t ) un (t )
3. Функциональное уравнение (2) записывается с учетом
выражения (3):
y(t) = bm um+1(t)+...+b1 u2(t)+b0 u1(t).
(5)
Совокупность уравнений (4) и (5) является системой уравнений,
которая может быть решена как на ЦВМ с применением различных
численных методов, так и на АВМ.
47.
Лайков, М.И. Автоматика и управление. Часть 1 - Иркутск:МГТУ ГА, 2010. с. 9-30











































 mathematics
mathematics








