Similar presentations:
Логические основы компьютеров
1. Логические основы компьютеров
1Логические
основы
компьютеров
Основы логики
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
2. Логика, высказывания
Логические основы компьютеров, 10 класс2
Логика, высказывания
Логика (др.греч. λογικος) – это наука о том, как
правильно рассуждать, делать выводы,
доказывать утверждения.
Формальная логика отвлекается от
конкретного содержания, изучает только
истинность и ложность высказываний.
Аристотель
(384-322 до н.э.)
Логическое высказывание – это
повествовательное предложение, относительно
которого можно однозначно сказать, истинно оно
или ложно.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
3. Высказывание или нет?
Логические основы компьютеров, 10 класс3
Высказывание или нет?
«Художники» — это только живописцы да
скульпторы.
Художник погиб жертвою грубой толпы.
Моего младшего брата нянчила высокая,
сухая, но очень стройная старушка, которую
звали Любовь Онисимовна.
Брат моложе меня на восемь лет.
Видишь, какое страшное?
На кого его зверство обрушится!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
4. Логика и компьютер
Логические основы компьютеров, 10 класс4
Логика и компьютер
Двоичное кодирование – все виды информации
кодируются с помощью 0 и 1.
Задача – разработать оптимальные правила
обработки таких данных.
Почему «логика»?
Результат выполнения операции можно
представить как истинность (1) или ложность (0)
некоторого высказывания.
Джордж Буль разработал основы алгебры,
в которой используются только 0 и 1
(алгебра логики, булева алгебра).
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
5. Логические основы компьютеров
5Логические
основы
компьютеров
Логические операции
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
6. Обозначение высказываний
Логические основы компьютеров, 10 класс6
Обозначение высказываний
}
A – Он был «тупейный художник».
B – Она «представляла на сцене».
!
простые высказывания
(элементарные)
Любое высказывание может быть ложно (0)
или истинно (1).
Составные высказывания строятся из простых с
помощью логических связок (операций) «и», «или»,
«не», «если … то», «тогда и только тогда» и др.
AиB
если A, то B
A тогда и только
тогда, когда B
К.Ю. Поляков, Е.А. Ерёмин, 2013
Он был «тупейный художник» и она
«представляла на сцене и танцевала танцы».
Если она «представляла на сцене и танцевала
танцы», то он был «тупейный художник».
Она «представляла на сцене и танцевала
танцы» тогда и только тогда, когда он был
«тупейным художником».
http://kpolyakov.spb.ru
7. Операция НЕ (инверсия)
Логические основы компьютеров, 10 класс7
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
A A
А
не А
0
1
1
0
А Простых людей ведь надо беречь
A Простых людей ведь не надо беречь
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
8. Операция И (логическое умножение, конъюнкция)
Логические основы компьютеров, 10 класс8
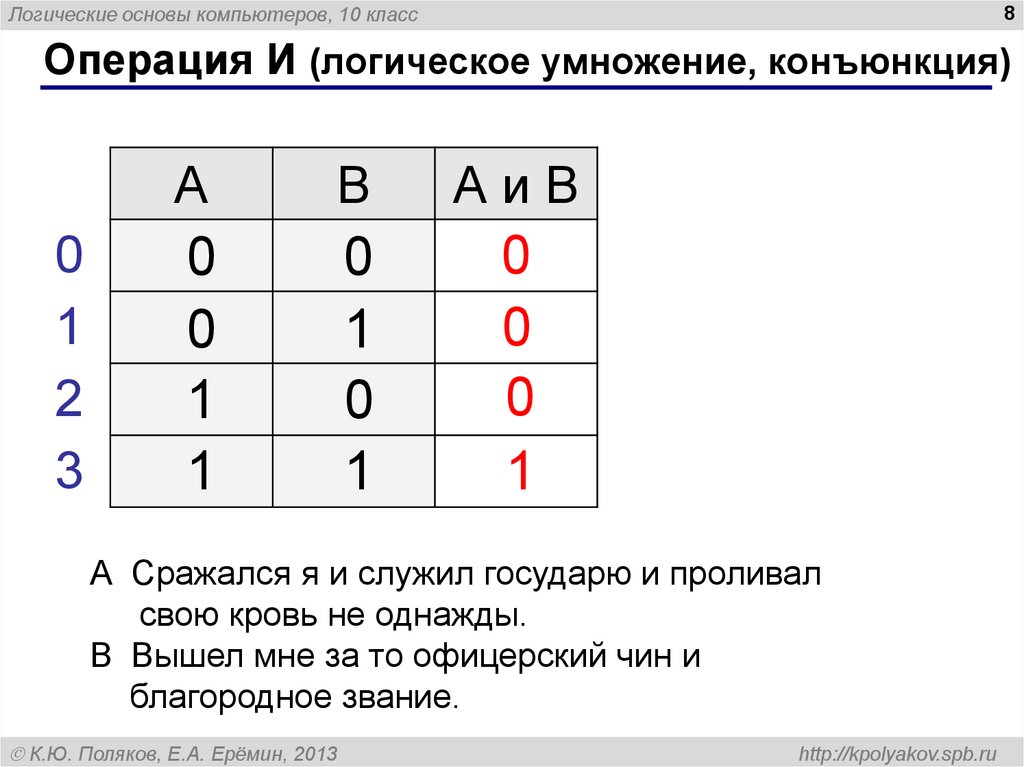
Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
А Сражался я и служил государю и проливал
свою кровь не однажды.
В Вышел мне за то офицерский чин и
благородное звание.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
9. Операция ИЛИ (логическое сложение, дизъюнкция)
Логические основы компьютеров, 10 класс9
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A B,
A or B (Паскаль),
A || B (Си)
…что-нибудь
одно: запорешь
или в солдаты
отдашь.
А Запорешь
В в солдаты отдашь
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
10. Импликация («если …, то …»)
Логические основы компьютеров, 10 класс10
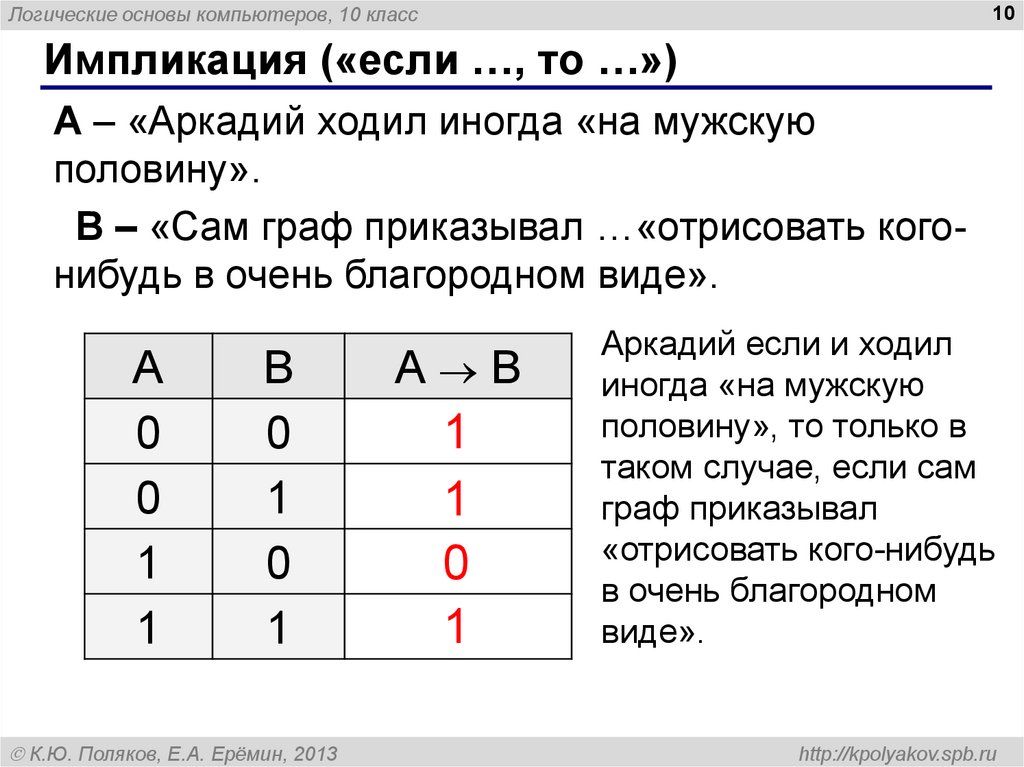
Импликация («если …, то …»)
A – «Аркадий ходил иногда «на мужскую
половину».
B – «Сам граф приказывал …«отрисовать когонибудь в очень благородном виде».
A
0
0
1
1
B
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
А B
1
1
0
1
Аркадий если и ходил
иногда «на мужскую
половину», то только в
таком случае, если сам
граф приказывал
«отрисовать кого-нибудь
в очень благородном
виде».
http://kpolyakov.spb.ru
11. Эквивалентность («тогда и только тогда, …»)
Логические основы компьютеров, 10 класс11
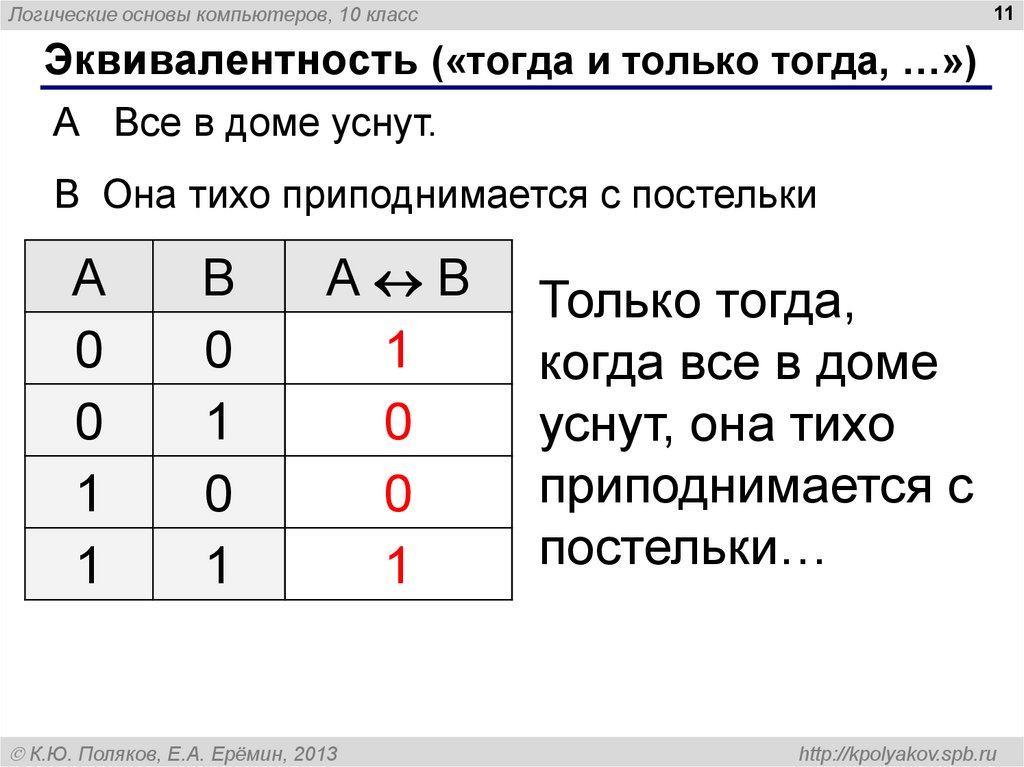
Эквивалентность («тогда и только тогда, …»)
А Все в доме уснут.
В Она тихо приподнимается с постельки
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
Только тогда,
когда все в доме
уснут, она тихо
приподнимается с
постельки…
http://kpolyakov.spb.ru








 informatics
informatics








