Similar presentations:
Параллелограмм
1. П а р а л л е л о г р а м м
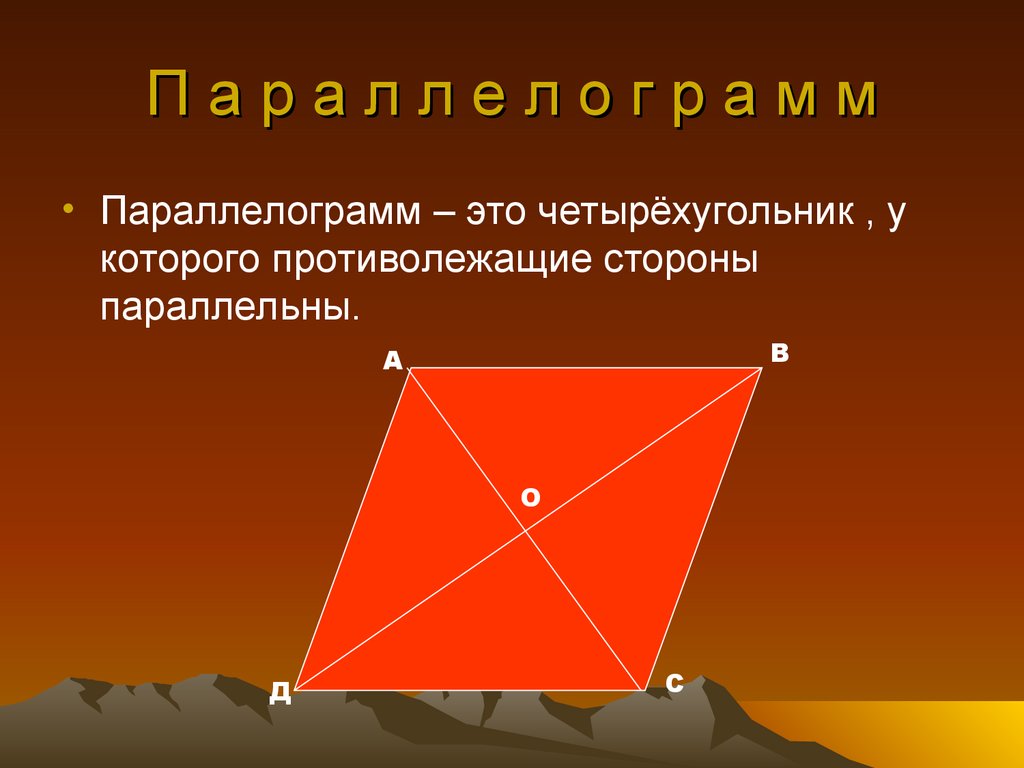
Параллелограмм• Параллелограмм – это четырёхугольник , у
которого противолежащие стороны
параллельны.
В
А
О
Д
С
2. Доказательство
• Пусть АВСД – данный четырёхугольник и О –точка пересечения его диагоналей
• Треугольники АОД и СОВ равны. У них углы
при вершине О равны как вертикальные, а
ОД=ОВ и ОА=ОС по условию теоремы.
Значит углы ОВС и ОДА равны, а они
являются внутренними накрест лежащими
для прямых АД и ВС и секущей ВД. По
признаку Параллельности прямых прямые АД
и ВС параллельны.
3. Т р е у г о л ь н и к
Треугольник• Треугольником называется фигура ,
которая состоит из трёх точек , не
лежащих на одной прямой ,и трёх отрезков
, попарно соединяющих эти точки.
4. П р я м о у г о л ь н и к
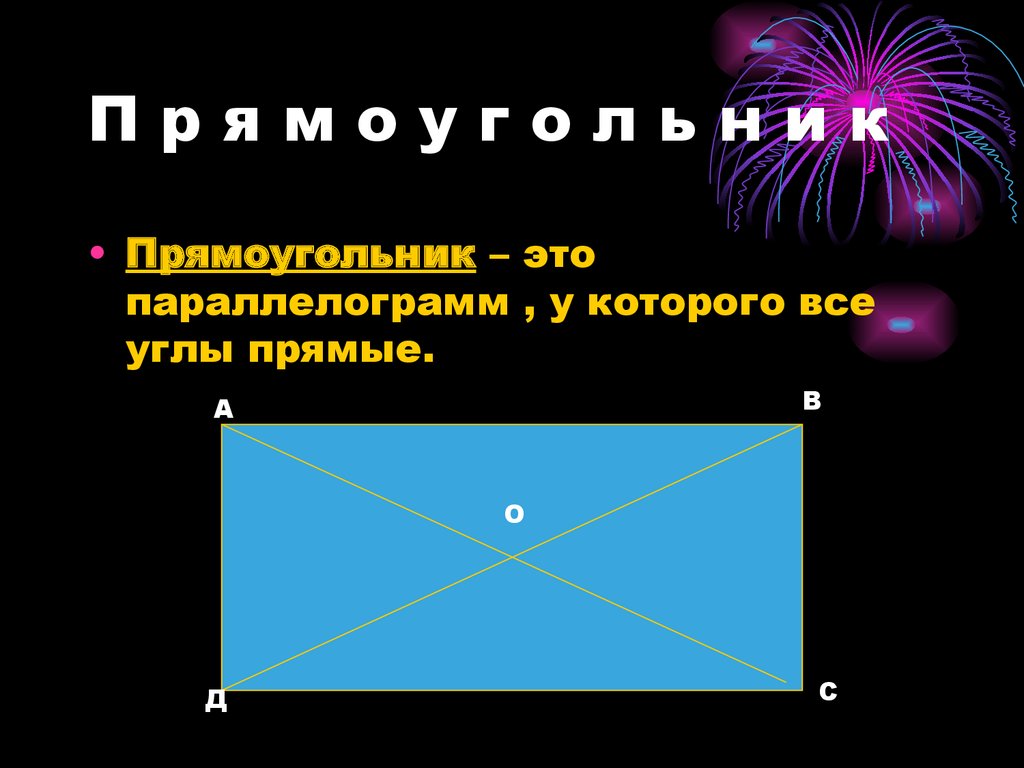
Прямоугольник• Прямоугольник – это
параллелограмм , у которого все
углы прямые.
В
А
О
Д
С
5. Т 6.4 Диагонали прямоугольника равны.
• Пусть АВСД – данный прямоугольник.Утверждение теоремы следует из равенства
прямоугольных треугольников ВАД и СДА. У них
углы ВАД и СДА прямые, катет АД общий, а
катеты АВ и СД равны как противолежащие
стороны параллелограмма. Из равенства
треугольников следует, что их гипотенузы
равны.
А
Д
В
С
6. Т р а п е ц и я
ТрапецияТрапецией называется
четырёхугольник , у которого только
две противолежащие стороны
параллельны
7. Доказательство
Пусть АВСД – данная трапеция. Проведёмчерез вершину В и середину Р боковой
стороны СД прямую. Она пересекает
прямую АД в некоторой точке Е.
Треугольники РВС и РЕД равны по второму
признаку равенства треугольников. У них
СР=ДР по построению, углы при вершине Р
равны как вертикальные, а углы РСВ и РДЕ
равны как внутренние накрест лежащие при
параллельных прямых ВС и АД и секущей
СД.
8. О к р у ж н о с т ь, в п и с а н н а я в т р е у г о л ь н и к
О к р у ж н о с т ь, в п и с а н н а яв треугольник
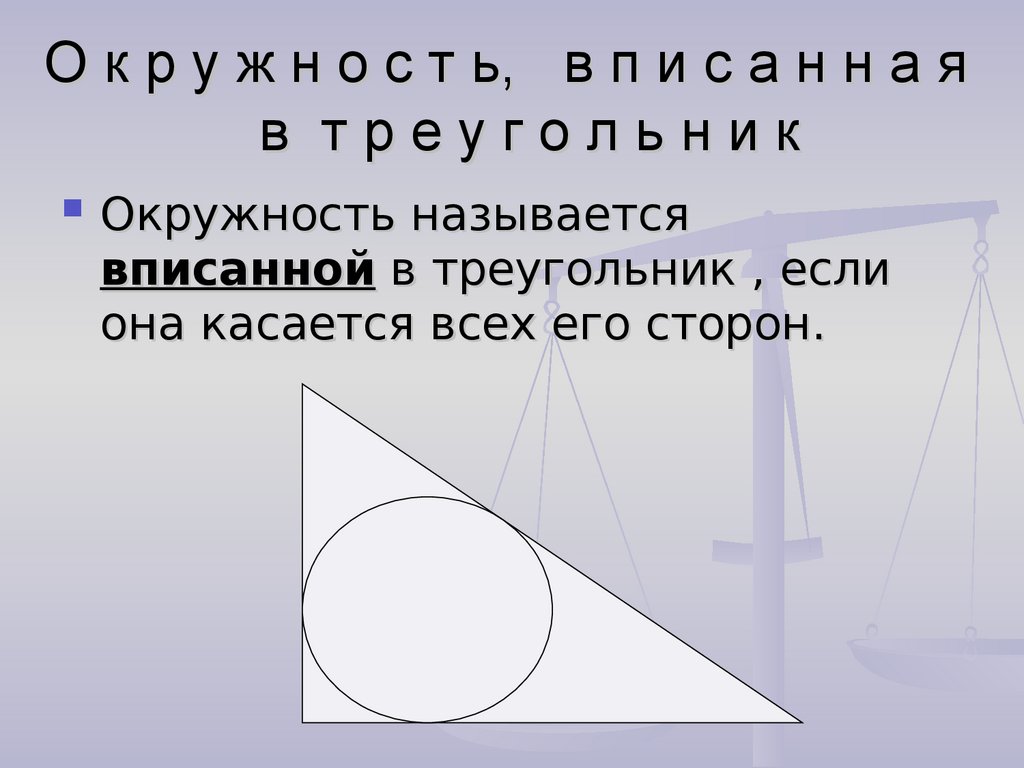
Окружность называется
вписанной в треугольник , если
она касается всех его сторон.
9. Доказательство
Пусть АВСD – данный треугольник, О –центр вписанной в него окружности, D, Е
и F – точки касания окружности со
сторонами. Прямоугольные треугольники
AOD и AOE равны по гипотенузе и катету.
У них гипотенуза АО общая, а катеты OD
и ОЕ равны как радиусы. Из равенства
треугольников следует равенство углов
OAD и ОАЕ. А это значит, что точка О
лежит на биссектрисе треугольника,
проведённой из вершины А.
10. О к р у ж н о с т ь, о п и с а н н а я о к о л о т р е у г о л ь н и к а
О к р у ж н о с т ь, о п и с а н н а яоколо треугольника
Окружность называется описанной
около треугольника, если она проходит
через все его вершины
11. Доказательство
Пусть АВС – данный треугольник и О –центр описанной около него
окружности. Треугольник АОС
равнобедренный: у него стороны ОА и
ОС равны как радиус. Медиана OD этого
треугольника одновременно является
его высотой. По этому центр окружности
лежит на прямой, перпендикулярной
стороне АС и проходящей и проходящей
через её середину.
12. О к р у ж н о с т ь
ОкружностьОкружностью называется фигура , которая
состоит из всех точек плоскости
равноудалённых от данной точки.
13. Т е о р е м а П и ф а г о р а
Теорема ПифагораТеорема 7.2
В прямоугольном
треугольнике квадрат
гипотенузы равен сумме
квадратов катетов.
14. Т е о р е м а Ф а л е с а
Теорема ФалесаТеорема
6.6
Если параллельные прямые,
пересекающие стороны угла, отсекают
на одной его стороне равные отрезки ,
то они отсекают равные отрезки и на
другой его стороне.
15. Признаки равенства треугольников
1признак : Если две стороны и угол междуними одного треугольника равны
соответственно двум сторонам и углу между
ними другого треугольника, то такие
треугольники равны.
2признак : Если сторона и прилежащие к ней
углы одного треугольника равны
соответственно стороне и прилежащим к ней
углам другого треугольника, то такие
треугольники равны.
3признак : Если три стороны одного
треугольника равны соответственно трём
сторонам другого треугольника, то такие
треугольники равны.












 mathematics
mathematics