Excel

1.

Excel - это компьютерная программа, разработанная компанией Microsoft,
предназначенная для работы с электронными таблицами. Она позволяет
пользователям создавать, редактировать, форматировать и анализировать
данные в таблицах, а также выполнять математические и статистические
операции, создавать графики и диаграммы. Excel часто используется в
различных областях, таких как бухгалтерия, финансы, статистика,
управление проектами, анализ данных и других.
• Excel был первоначально выпущен в 1985 году компанией
Microsoft.
• Excel также поддерживает работу с многомерными
таблицами, что упрощает анализ больших наборов данных.
• Excel предлагает различные функции и инструменты для
обработки данных, такие как сортировка, фильтрация,
поиск, подсчет суммы и других математических операций.
• Excel широко используется в бизнесе, учреждениях и
образовании для работы с данными, составления отчётов,
анализа и прогнозирования.
• С Excel было разработано множество дополнительных
функций и инструментов сторонних разработчиков, которые
расширяют его возможности и упрощают работу с данными.

2.

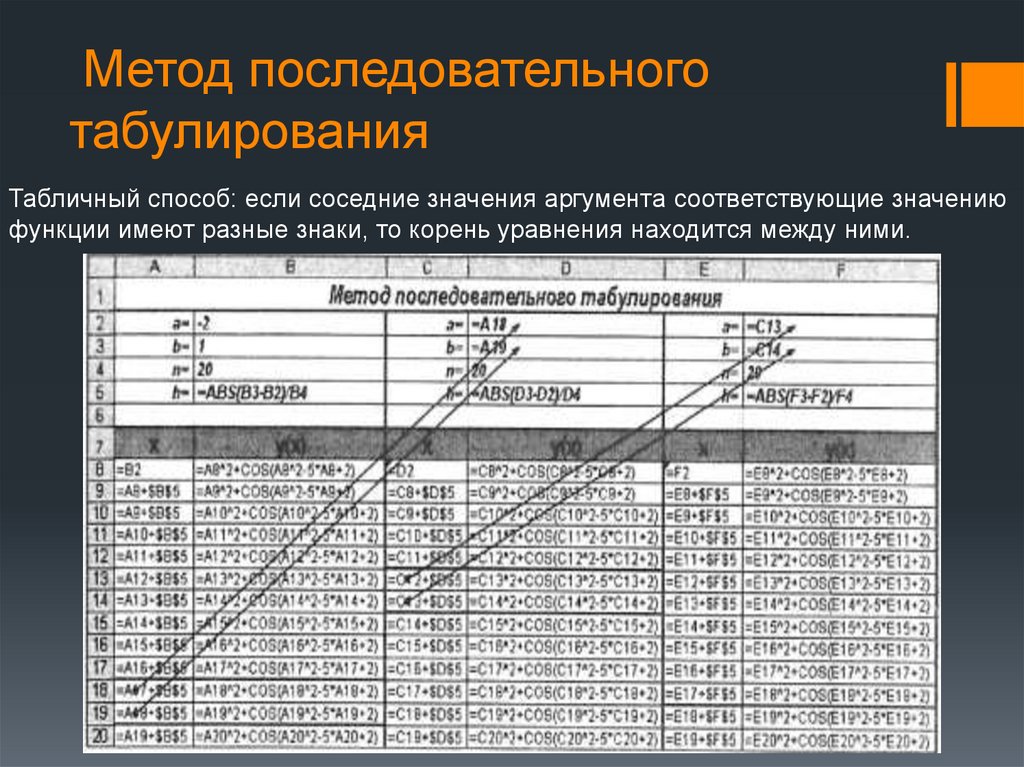
Метод последовательного
табулирования
Табличный способ: если соседние значения аргумента соответствующие значению
функции имеют разные знаки, то корень уравнения находится между ними.

3.

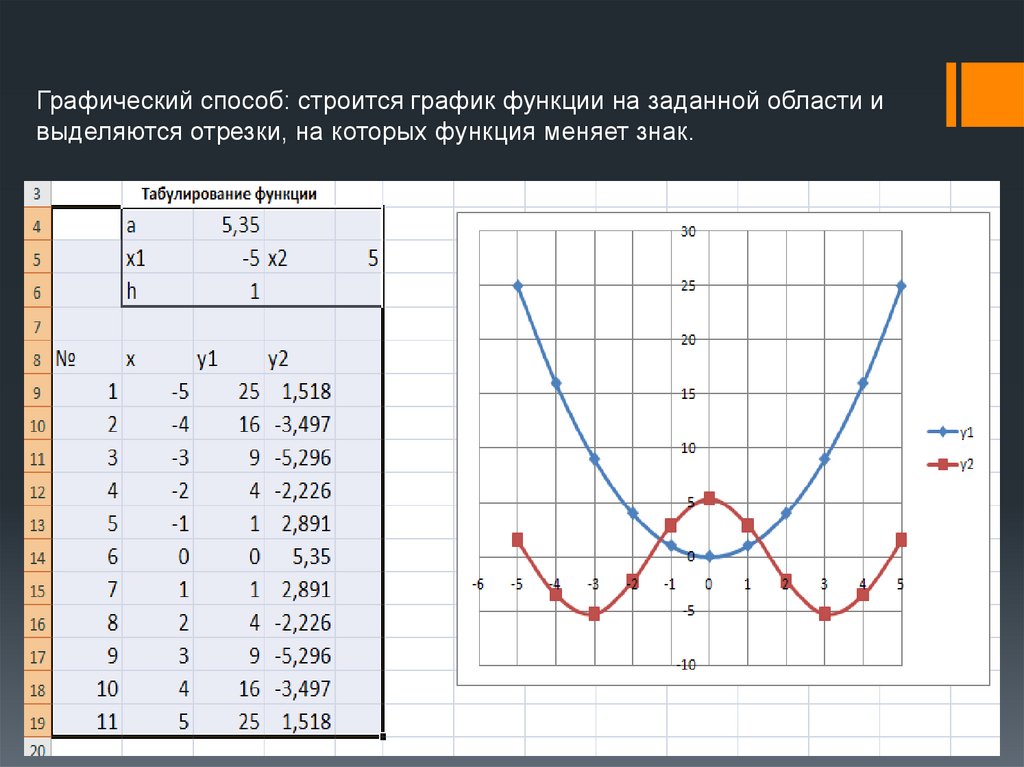
Графический способ: строится график функции на заданной области и
выделяются отрезки, на которых функция меняет знак.

4.

Метод Ньютона
Заключается в том, что если xn - некоторое приближение к корню x’ , то
следующее приближение определяется как корень касательной к функции f(x),
проведенная в точке xn. Этот метод является наиболее эффективным,
поскольку обеспечивает сходимость за минимальные количество шагов
Алгоритм применения метода Ньютона:
✓ определяем начальное приближение x0;
✓ составляем таблица расчета с последовательным построением итераций по
формулам Ньютона: для первого шага в качестве аргумента используем
начальное приближение x0, для последующих шагов - значение корня в
предыдущем шаге, т. е. значение xi;
✓ условием завершения процедуры уточнения корня является достижение
функцией значения, меньше заданного.

5.

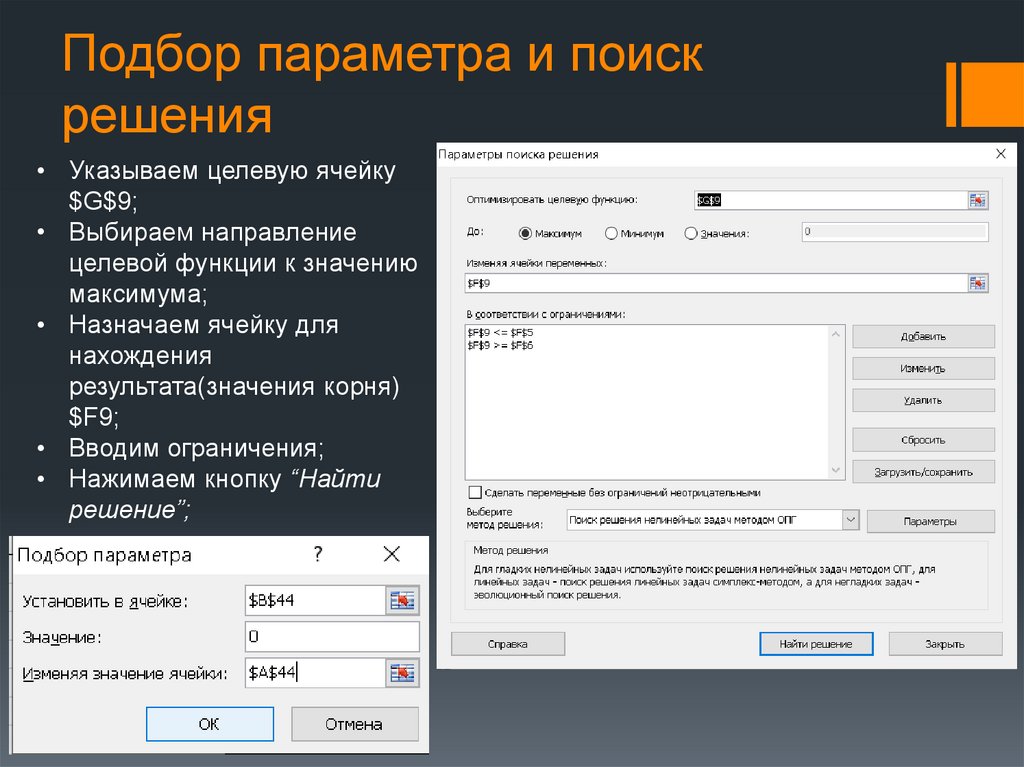
Подбор параметра и поиск
решения
• Указываем целевую ячейку
$G$9;
• Выбираем направление
целевой функции к значению
максимума;
• Назначаем ячейку для
нахождения
результата(значения корня)
$F9;
• Вводим ограничения;
• Нажимаем кнопку “Найти
решение”;

6.

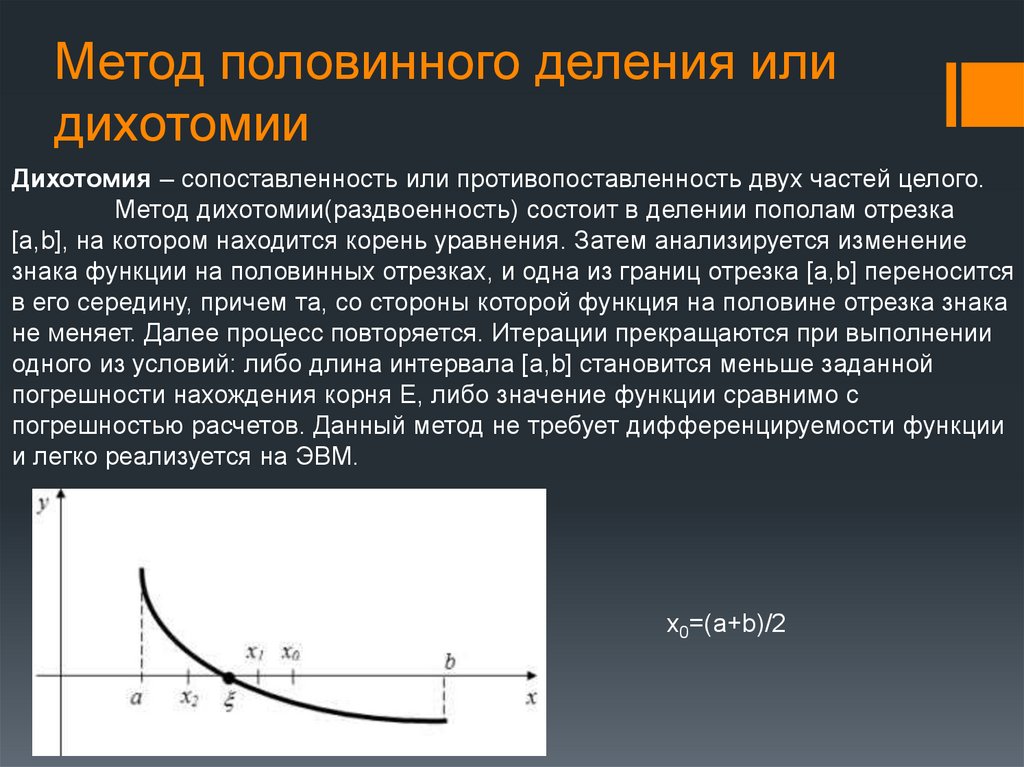
Метод половинного деления или
дихотомии
Дихотомия – сопоставленность или противопоставленность двух частей целого.
Метод дихотомии(раздвоенность) состоит в делении пополам отрезка
[а,b], на котором находится корень уравнения. Затем анализируется изменение
знака функции на половинных отрезках, и одна из границ отрезка [а,b] переносится
в его середину, причем та, со стороны которой функция на половине отрезка знака
не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении
одного из условий: либо длина интервала [a,b] становится меньше заданной
погрешности нахождения корня E, либо значение функции сравнимо с
погрешностью расчетов. Данный метод не требует дифференцируемости функции
и легко реализуется на ЭВМ.
x0=(a+b)/2

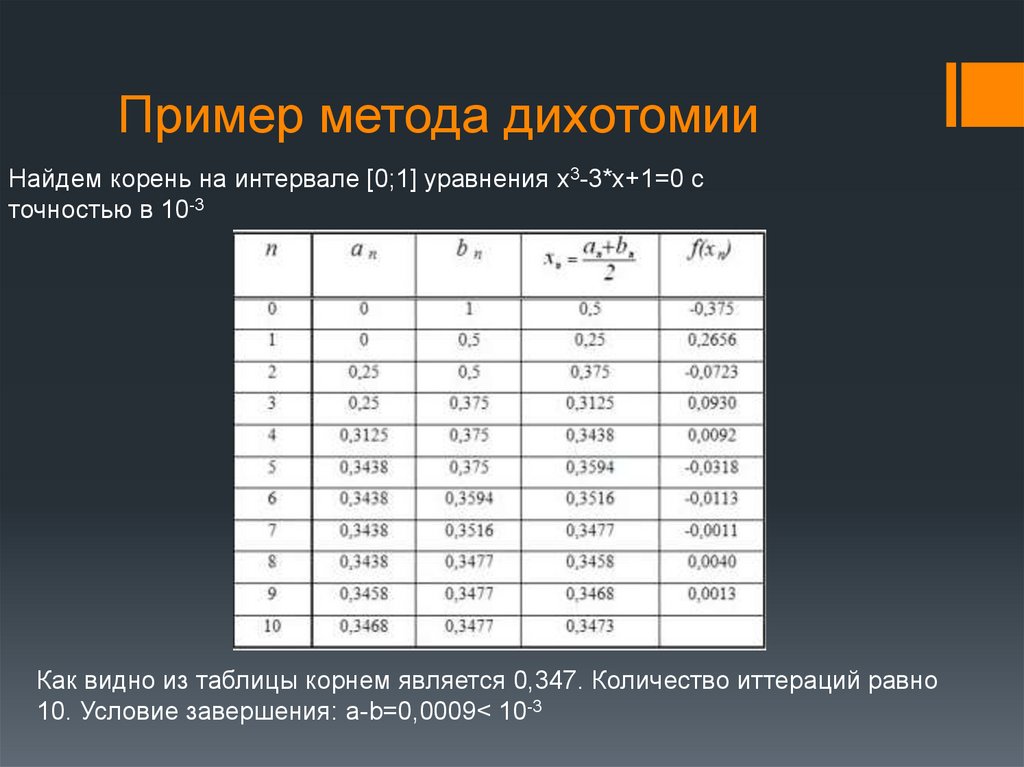
7.

Пример метода дихотомии
Найдем корень на интервале [0;1] уравнения x3-3*x+1=0 с
точностью в 10-3
Как видно из таблицы корнем является 0,347. Количество иттераций равно
10. Условие завершения: a-b=0,0009< 10-3

8.

Метод золотого сечения