Применение свойств функций для решения уравнений. Монотонность функций

1. Применение свойств функций для решения уравнений

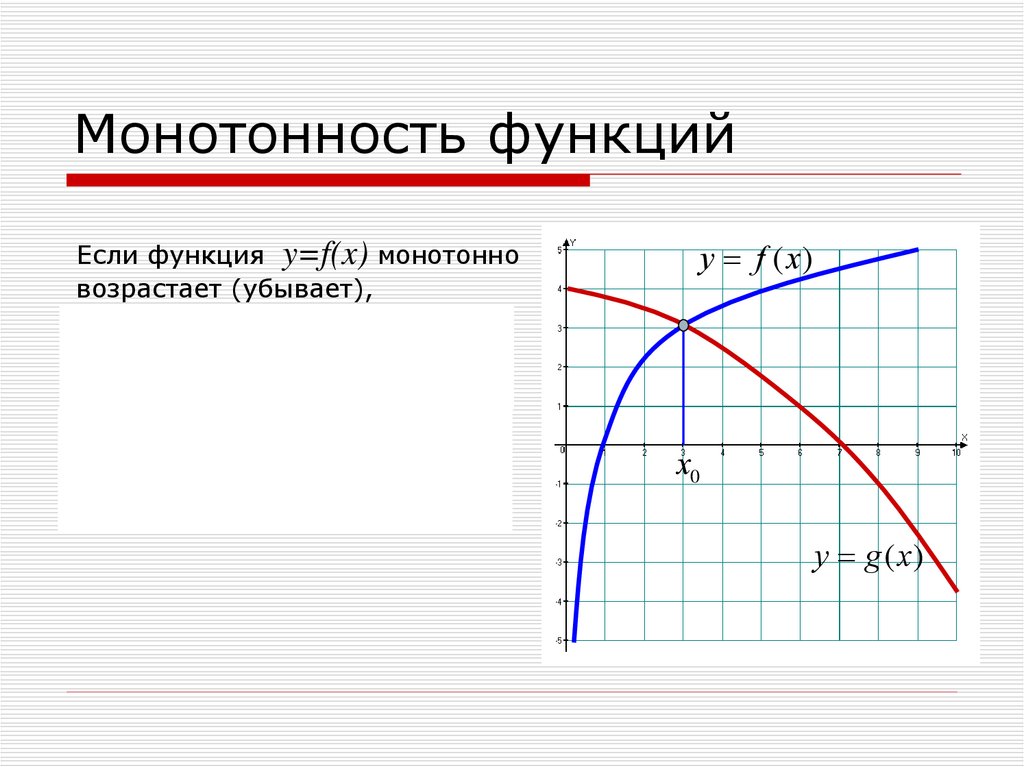
2. Монотонность функций

Если функция y=f(x) монотонно
возрастает (убывает),
а функция y=g(x)
монотонно убывает (возрастает)
на некотором промежутке и
х0– корень уравнения
f(x)=g(x),
у f ( x)
х0
то он единственный.
у g ( x)

3. Решить уравнение

2
Очевидно, что
Функция
х 2
х 2
x
log 1 4
3 2
– корень данного уравнения.
f x 23 х 4
x
g x log 1 4
3 2
3 х 4
- возрастающая, а функция
- убывающая на промежутке
- единственный корень уравнения.
Ответ: 2.
; .

4. Решить уравнение

2
2
2 х х 2 х 2 х 8 х 11 3.
Решить данное уравнение стандартными методами
не представляется возможным, поэтому начнем решение
с нахождения области определения уравнения:
2 х х 2 0,
2
х 2 х 8 0,
х 11 0;
2 х 1,
х 2; х 4,
х 11;
-2
х 2.
Ответ: -2.
Закрыть
1
-2
-11
Проверим, является ли х = -2 корнем данного уравнения:
2 2 22 2 22 2 2 8 2 11 3.
-2
4

English Русский Rules