Алгебра и начала анализа. А.Г. Мордкович, профильный уровень. 10 класс

1.

Алгебра и начала анализа.
А.Г. Мордкович, профильный уровень
10 класс

2.

Содержание
1.Комплексные числа и операции над ними
2.Комплексные числа и координатная
плоскость
3.Тригонометрическая форма записи
комплексного числа
4.Комплексные числа и квадратные уравнения
5.Возведение комплексного числа в степенью
Извлечение кубического корня из
комплексного числа

3.

4.

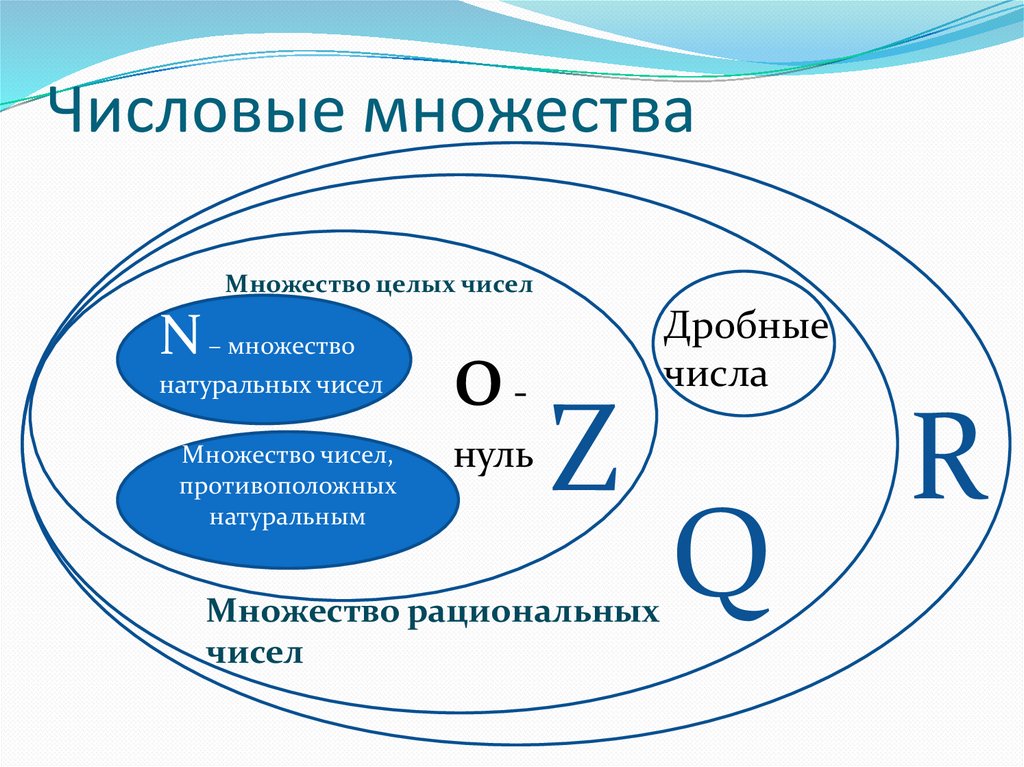
Числовые множества
Множество целых чисел
N – множество
натуральных чисел
Множество чисел,
противоположных
натуральным
0нуль
Дробные
числа
Z
Множество рациональных
чисел
Q
R

5.

Перед нами числовые множества, свойства
которых мы изучали в курсе средней школы.
Мы знаем, что с элементами этих числовых
множеств можно совершать следующие
алгебраические операции:
• сложение,
• вычитание,
• умножение,
• деление,
• извлечение корней из неотрицательных чисел.

6.

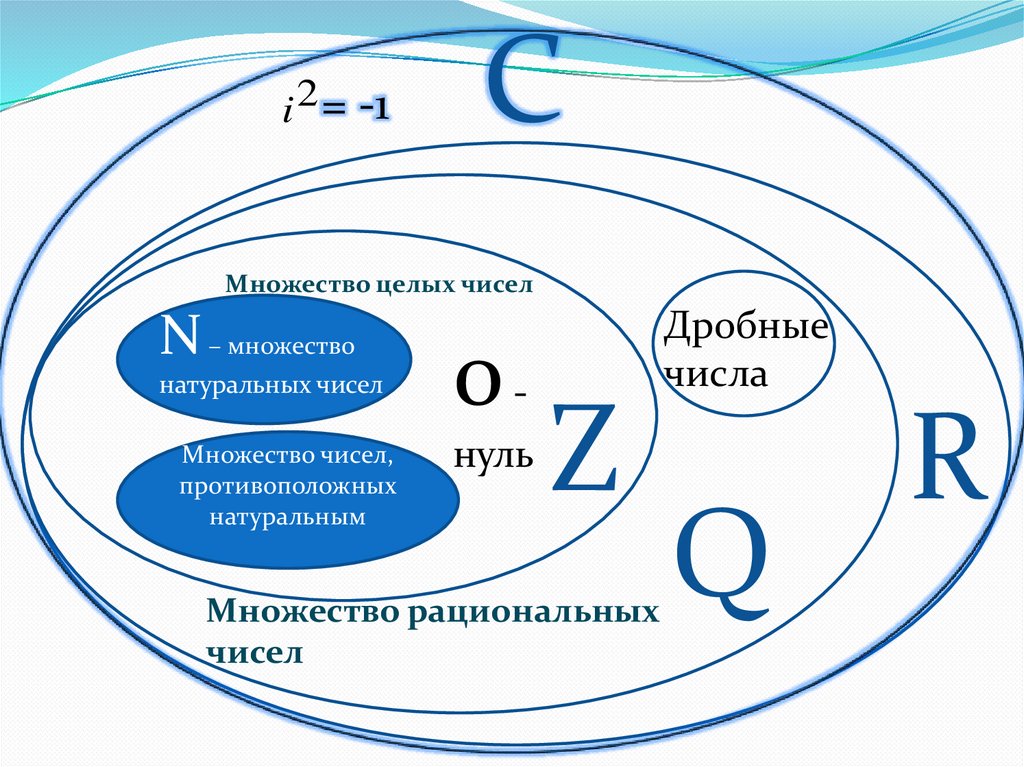
i 2 = -1
C
Множество целых чисел
N – множество
натуральных чисел
Множество чисел,
противоположных
натуральным
0нуль
Дробные
числа
Z
Множество рациональных
чисел
Q
R

7.

Таким образом, схема расположения основных числовых
множеств имеет вид:
N Z Q R C.
Появилось новое число, которое называют мнимая
единица:
2
i
= -1.
Произведение мнимой единицы и действительного числа
называют чисто мнимым числом.
Например, -4i, 0,3i, 15i, 10
i.

8.

Определение комплексного
числа
Комплексным числом называют
сумму действительного числа и чисто
мнимой части.
Z = a + bi C
a R, b R, i – мнимая единица.
Приведите примеры комплексных
чисел.

9.

Два комплексных числа называются равными, если равны их
действительные и мнимые части.
a + bi = c + di a=c, b=d
Арифметические операции над комплексными числами
выполняются по известным Вам алгебраическим правилам:
1. z1+ z2= a + bi + c + di = (a+c) + (b+d)i.
2. z1- z2= (a + bi) – (c + di) = (a-c) + (b-d)i.
3. z1• z2= (a + bi) • (c + di) = (ac-bd) + (bc+ad)i.
Для частного 2 комплексных чисел тоже можно вывести формулу,
но лучше запомнить правило: при делении 2 комплексных
чисел нужно умножить числитель и знаменатель полученной
дроби на число, сопряжённое знаменателю.

10.

11.

Геометрической моделью множества С является
координатная плоскость.
Каждому комплексному числу Z = a + bi можно
поставить в соответствие точку координатной плоскости
(a; b).
Причём, по оси абсцисс откладывается действительная
часть числа, а по оси ординат – мнимая.
Построим число z1= 3+2i.
Y
z1
2
0
3
X

12.

Любую точку на координатной плоскости можно
воспринимать двояко: алгебраически, как
упорядоченную пару (a; b)действительных чисел, и
как вектор с началом в точке (0; 0) и концом в точке
(a; b). При векторном подходе получают смысл
операции сложения, вычитания и умножения.
Y
z1
2
0
3
X

13.

14.

Определение модуля
комплексного числа.
Модулем комплексного числа z = a + bi называют
2
2
число a b . Обозначение: ІzІ.
Модуль комплексного числа равен 1 тогда и только
тогда, когда соответствующая ему точка координатной
плоскости лежит на числовой окружности.

15.

Если комплексное число z = a + bi лежит на числовой
окружности, то z = cosα + i sinα для некоторого
действительного числа α; если z = cosα + i sinα , то z
лежит на числовой окружности.
Y
z
sinα
X
cosα 0
-1
1

16.

Тригонометрической формой
записи
отличного от нуля комплексного числа z называют его
запись в виде z = ρ(cosα + i sinα) , где ρ– положительное
действительное число.
Теорема. Всякое отличное от нуля комплексное число z ,
может быть записано в виде z = ІzІ(cosα + i sinα), где α –
некоторое действительное число.
Если z = ρ(cosβ + i sinβ) - другая тригонометрическая
запись числа z, то ρ = ІzІ и β – α = 2πk, k Z.

17.

Задание: Записать в тригонометрической
форме число 2 – 2i 3 .
Решение. z = ІzІ(cosα + i sinα)
1. Найдём модуль числа z = 2 – 2i 3 . Получим ІzІ =
Значит, z = 4( 2 2 3 i ).
4
2 ( 2 3)
2
2
=4.
4
2. Осталось вычислить аргумент α, исходя из следующих
соображений: cosα = 1 , sinα = - 3 , -π<α<π. Этим условиям
2
удовлетворяет число α = - . 2
3
3
3. Получили, 2 – 2i = 4(cos(- )+ i sin(- 3 )).
3

18.

19.

Квадратным корнем из комплексного числа z
называют комплексное число, квадрат которого равен
z.
Множество всех квадратных корней из комплексного
числа z обозначают z .
Значит, теперь мы можем найти корни квадратных
уравнений, имеющих отрицательный дискриминант:
если d < 0, то d = ± d ∙i .
Пример. Решите уравнение z2 – 2z + 2 =0.
D1 = 12 2 1 ; z1,2= 1± 1 = 1± i.
Ответ: 1± i.

20.

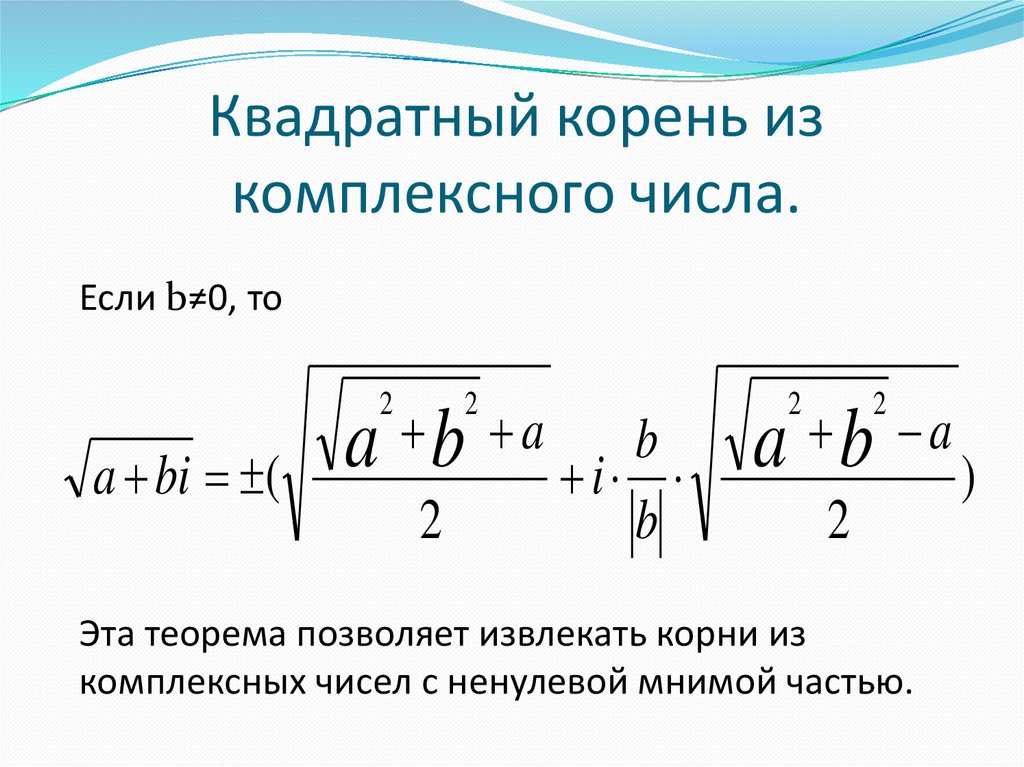
Квадратный корень из
комплексного числа.
Если b≠0, то
a b a i b a b a )
2
a bi (
2
2
2
b
2
2
Эта теорема позволяет извлекать корни из
комплексных чисел с ненулевой мнимой частью.

21.

15 8i
Вычислите
Решение.
15 8i
15 8
2
=±(
2
17
17 15
2
8
+i∙ ∙
8
17 15
2
)=±(4+i).
Самостоятельно выполните №35.13 (в).
7 i
Ответ: ±
.
2
Теперь можно извлечь корень из любого
комплексного дискриминанта.

22.

23.

Формула Муавра.
(ρ(cosα + i sinα))n=ρn(cos nα + i sin nα)),
n N.
Задание.
Вычислить: (2(cos 15° +i sin 15°)6 .
Решение.
(2(cos 15° +i sin 15°)6 = 26(cos (15°∙6) +i sin (15°∙6))=
=64(cos 90° +i sin 90°)=64i.

24.

Извлечение кубического корня из
комплексного числа.
Теорема.
3
2 k
2 k
3
z z (cos
i sin
) k 0,1,2
3
3
Задание классу:
§§ 32-36, выписать примеры с решениями.
Выполнить домашнюю контрольную работу