Комплексные числа и координатная плоскость. 10 класс

1. Урок по алгебре в 10 классе

Комплексные числа и
координатная
плоскость

2. Подобно тому, как всю область действительных величин можно представить с помощью бесконечной прямой, можно себе представить

область всех величин,
действительных и мнимых с помощью
бесконечной плоскости, где каждая точка,
определенная своей абсциссой а и своей
ординатой b, представляет в то же время
величину a+bi.
К. Гаусс

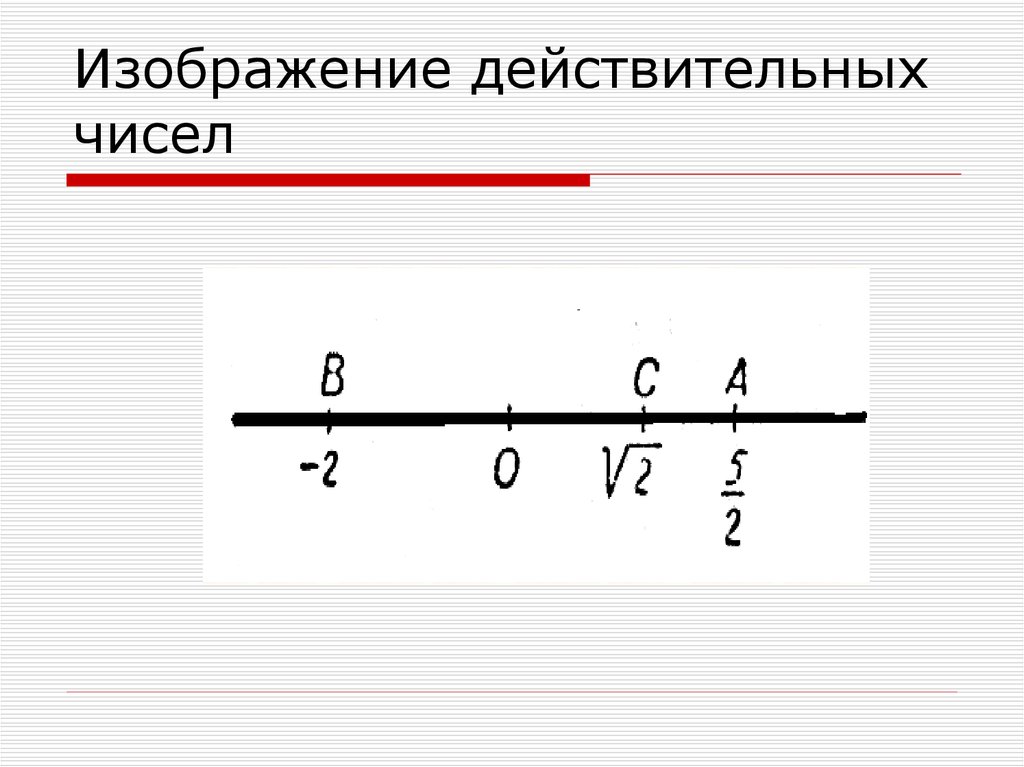
3. Изображение действительных чисел

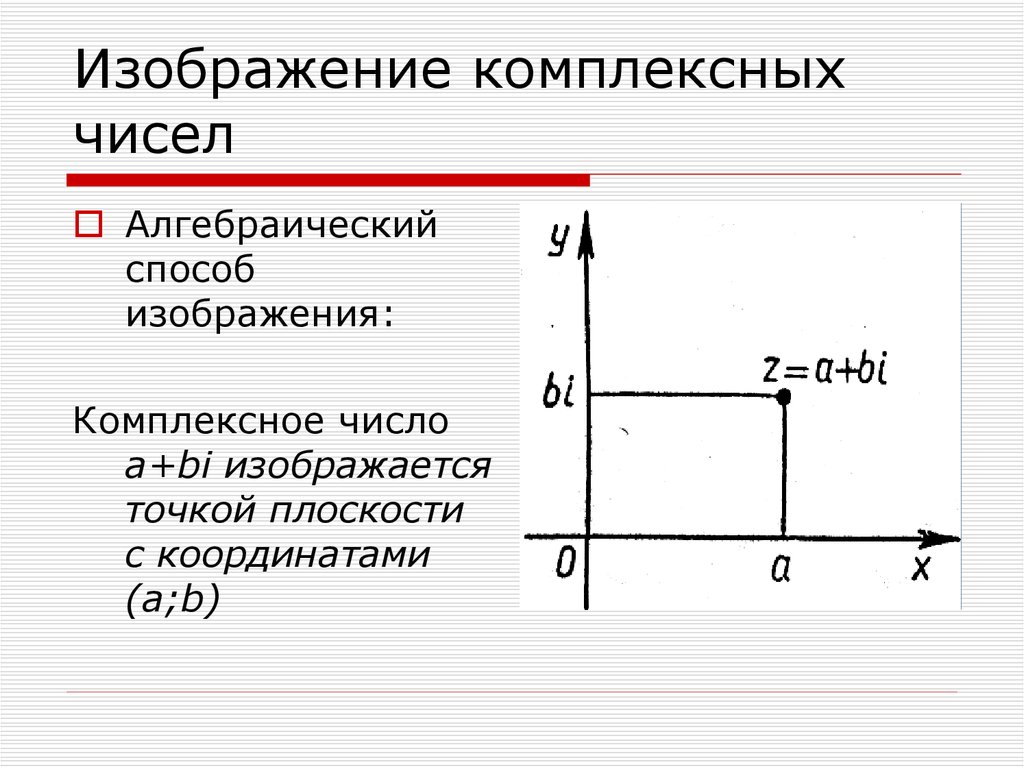
4. Изображение комплексных чисел

Алгебраический
способ
изображения:
Комплексное число
a+bi изображается
точкой плоскости
с координатами
(a;b)

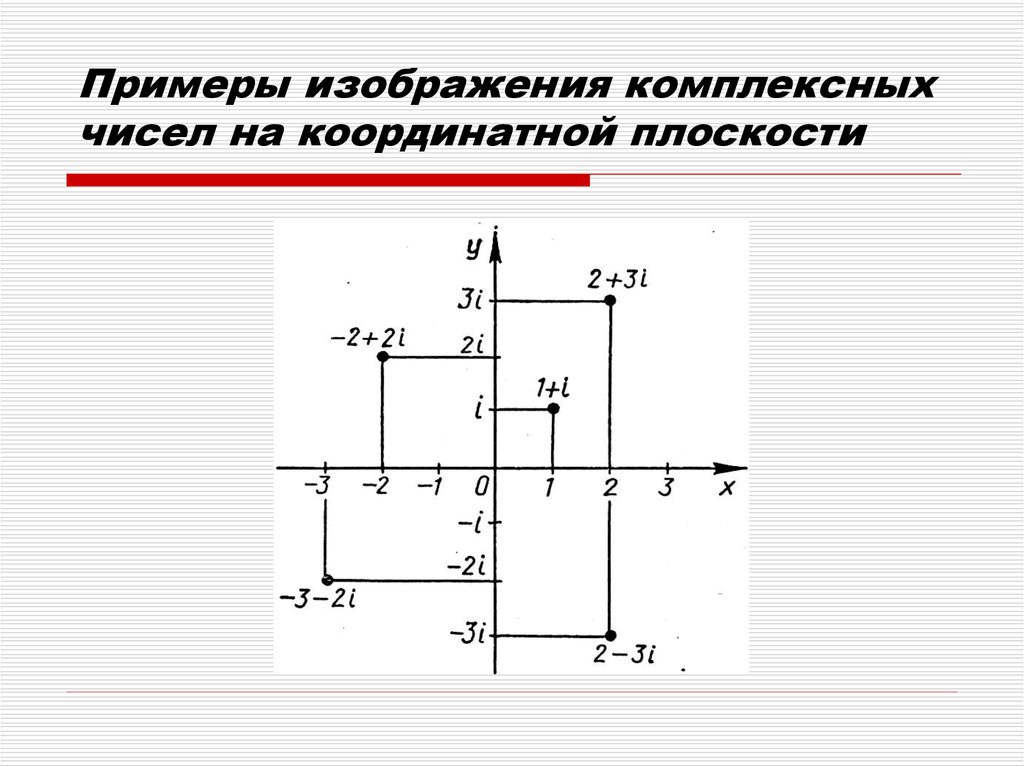
5. Примеры изображения комплексных чисел на координатной плоскости

6. Изобразите на координатной плоскости множество всех комплексных чисел, у которых:

(Нас интересуют
комплексные числа
z=x+yi , у которых
х=-4. Это-уравнение
прямой,
параллельной оси
ординат)
у
Х= - 4
Действительная
часть равна -4
0
х

7. Изобразите на координатной плоскости множество всех комплексных чисел, у которых:

Мнимая часть
является четным
однозначным
натуральным
числом
(Нас интересуют
комплексные числа
z=x+yi, у которых
у=2,4,6,8.
Геометрический образ
состоит из четырех
прямых,параллельных
оси абсцисс)
у
8
6
4
2
0
х

8. Изображение комплексных чисел

Векторный способ
изображения:
Каждое комплексное
число z=a+bi
изображается на
плоскости как вектор ОА
с началом в начале
координат и с концом
в точке А(a;b)

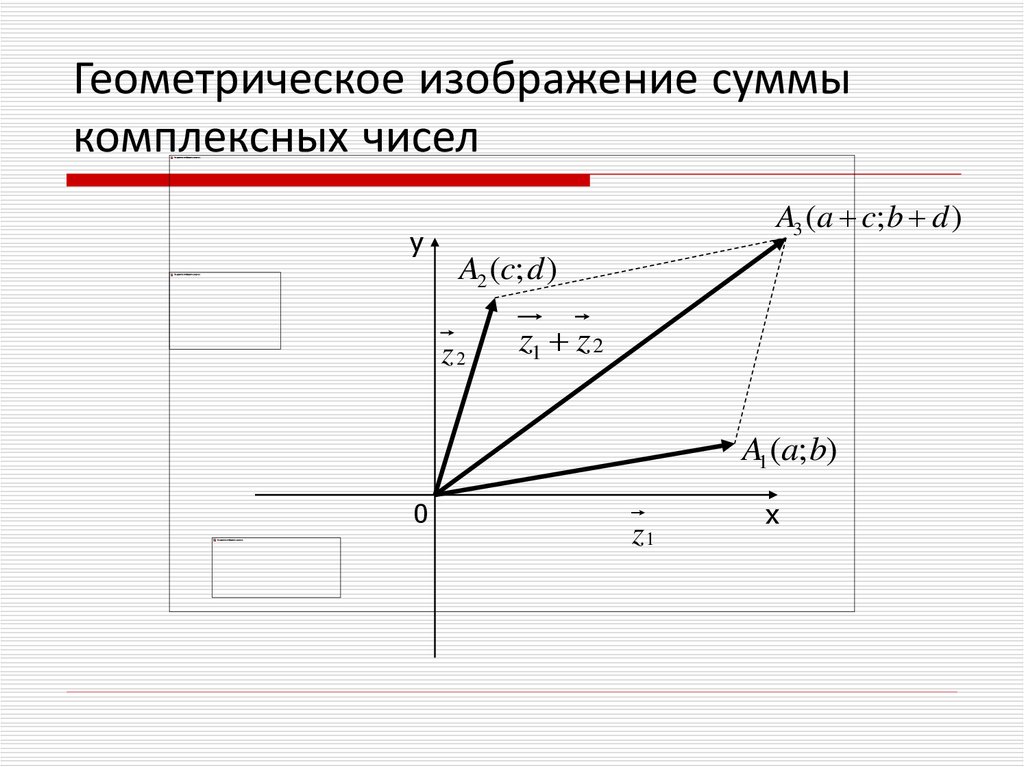
9. Геометрическое изображение суммы комплексных чисел

A3 (a c; b d )
у
A2 (c; d )
z2
z1 z 2
A1 (a; b)
0
z1
х

10. Изображение противоположных комплексных чисел

M ( a; b )
у
z
0
z
х
N ( a; b)

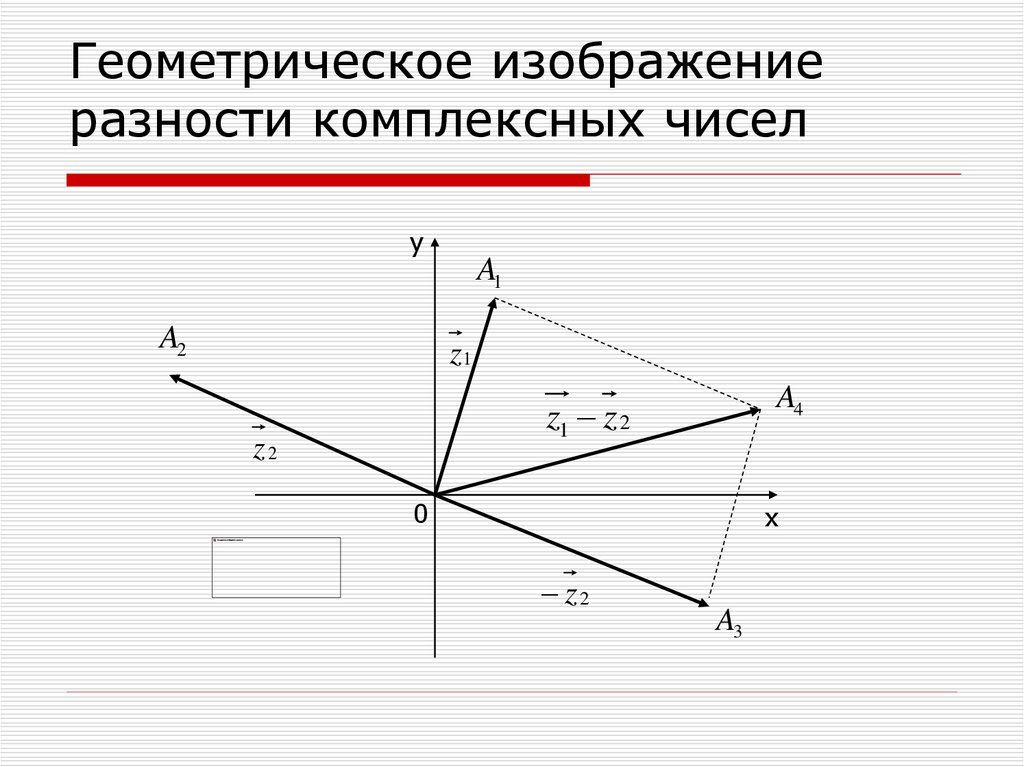
11. Геометрическое изображение разности комплексных чисел

у
A1
A2
z1
A4
z1 z 2
z2
0
х
z2
A3

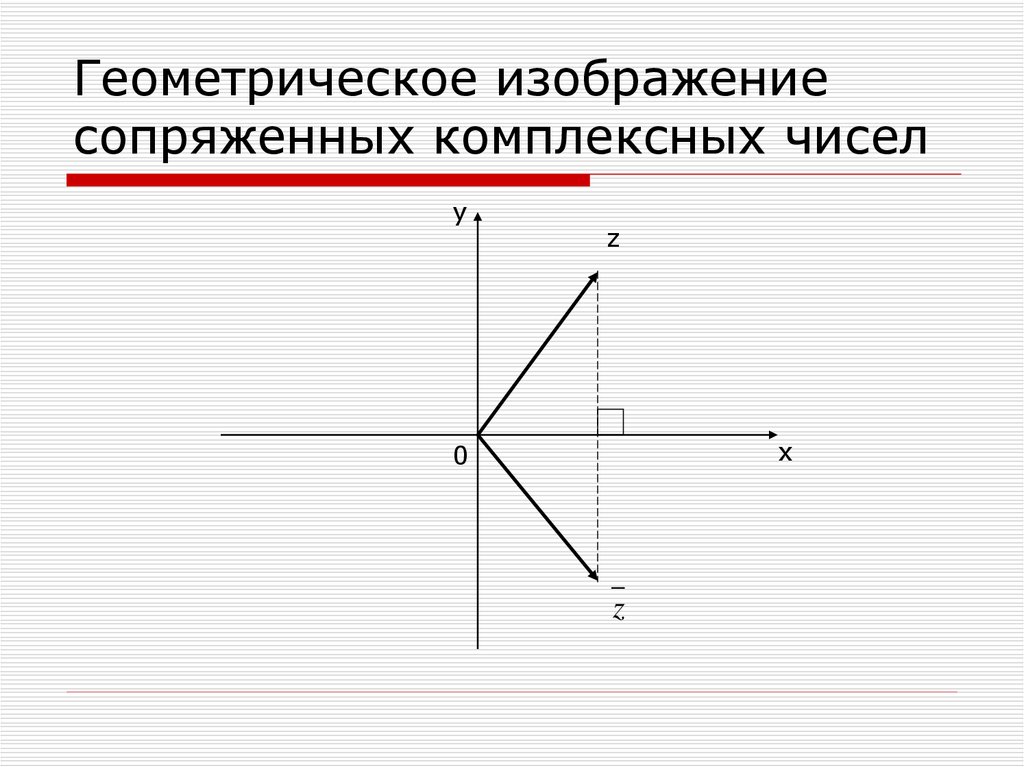
12. Геометрическое изображение сопряженных комплексных чисел

у
z
х
0
z

13. Самостоятельная работа

Вариант 1
Постройте точки,
соответствующие
комплексным числам:-1;
3+4i, 2-3i, -5+2i.
Найти сумму и разность
комплексных чисел:
а) z= - 2 + i, z = 3 +(-1)i;
б) z = 2+3i, z = 2 + (-3)i;
в) z = 1-2i, z =-1-2i,
г) z= 3i; z=2+0i.
Что представляет
геометрическое множество
всех комплексных чисел:
а) х=2
б) Imz=2Rez
в) -2≤x≤0 и 1≤у≤3.
Вариант 2
Постройте точки,
соответствующие
комплексным числам: -8-7i,
2i, -3i, 1.
Найти сумму и разность
комплексных чисел:
а) z= 2 + (-1) i, z= 0 + 2i,
б) z= -3,
z= 4i
в) z = 1+ (-2)i, z = -1+ 2i,
г) z = 2 + (-2) i, z = -1 + i.
Что представляет
геометрическое множество
всех комплексных чисел :
а) 1 ≤ х ≤3; б) 0 ≤ у ≤ 2;
в) Rez=Imz.