Построение треугольника по трем элементам

1.

«Построение
треугольника
по трем
элементам»

2.

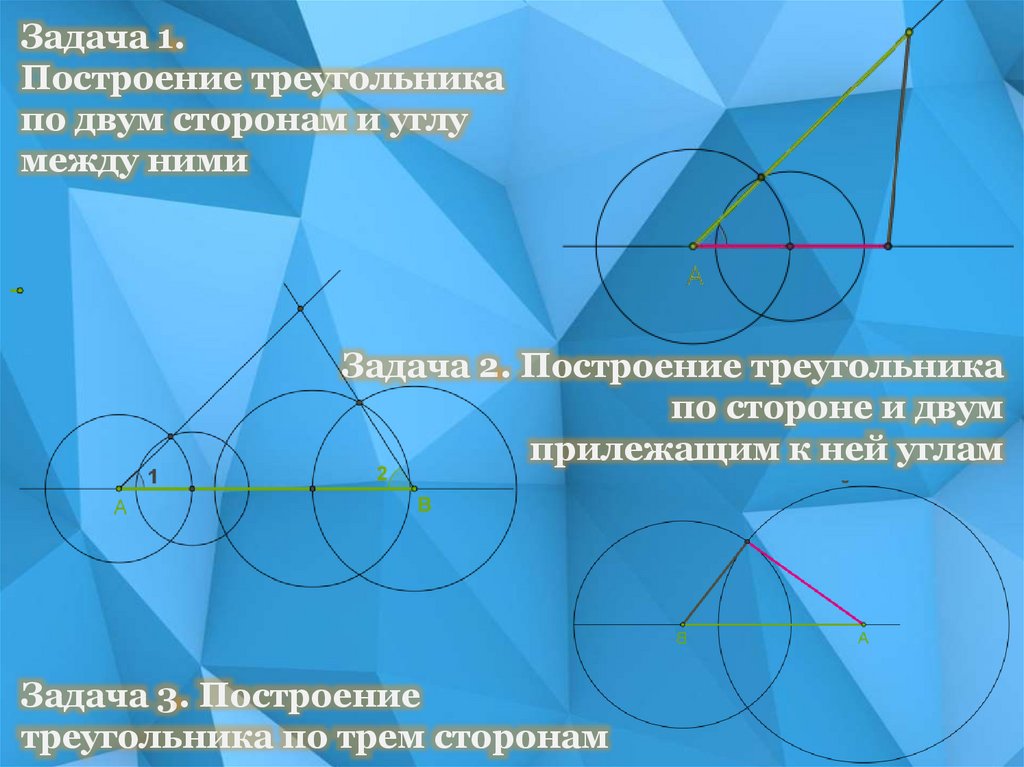
Задача 1.
Построение треугольника
по двум сторонам и углу
между ними
Задача 2. Построение треугольника
по стороне и двум
прилежащим к ней углам
Задача 3. Построение
треугольника по трем сторонам

3.

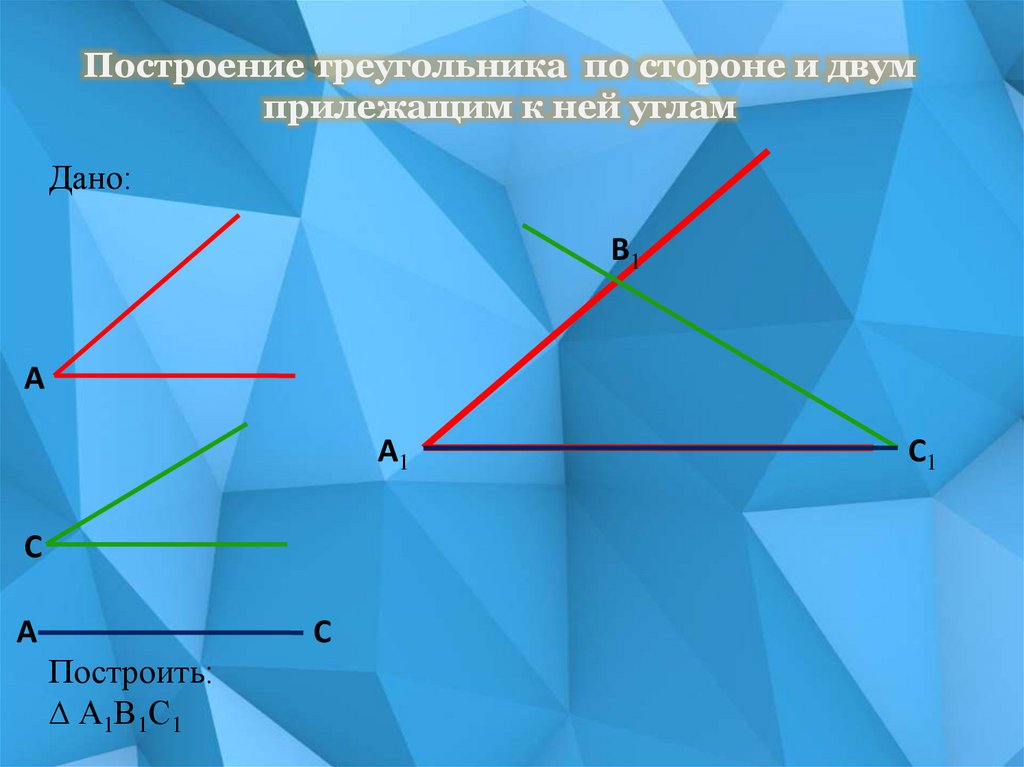
Построение треугольника по стороне и двум
прилежащим к ней углам
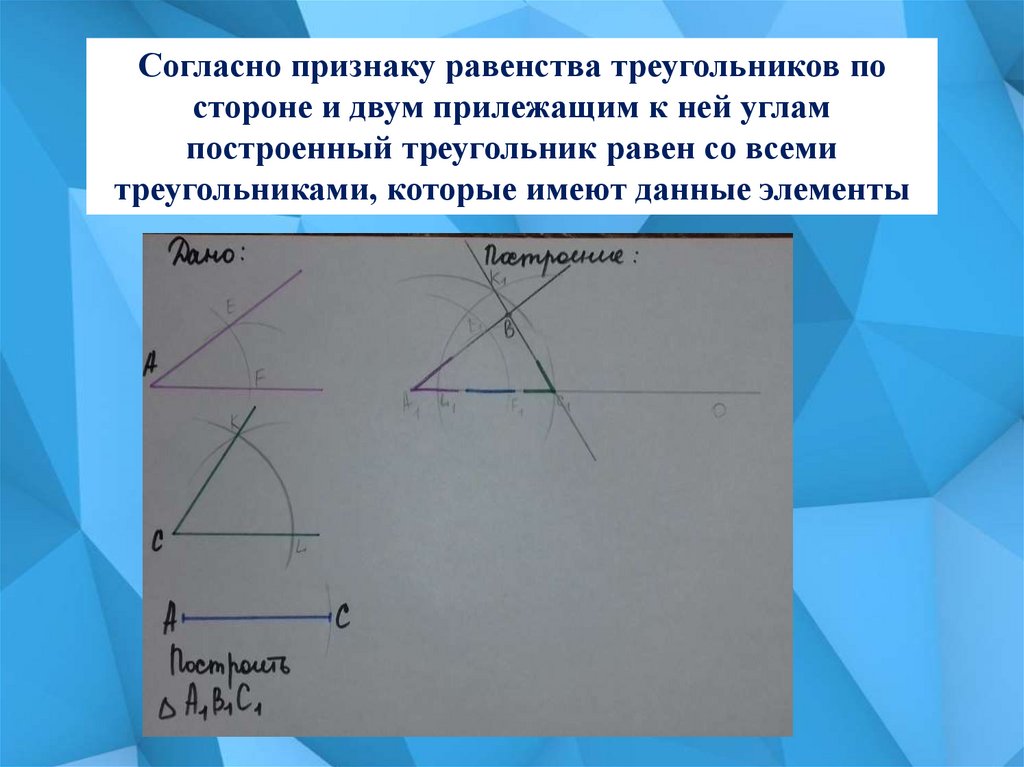
Дано:
В1
А
А1
С
А
С
Построить:
∆ А1В1С1
С1

4.

План действий:
1. Построить угол А
2. Построить отрезок АС
3. Построить угол С

5.

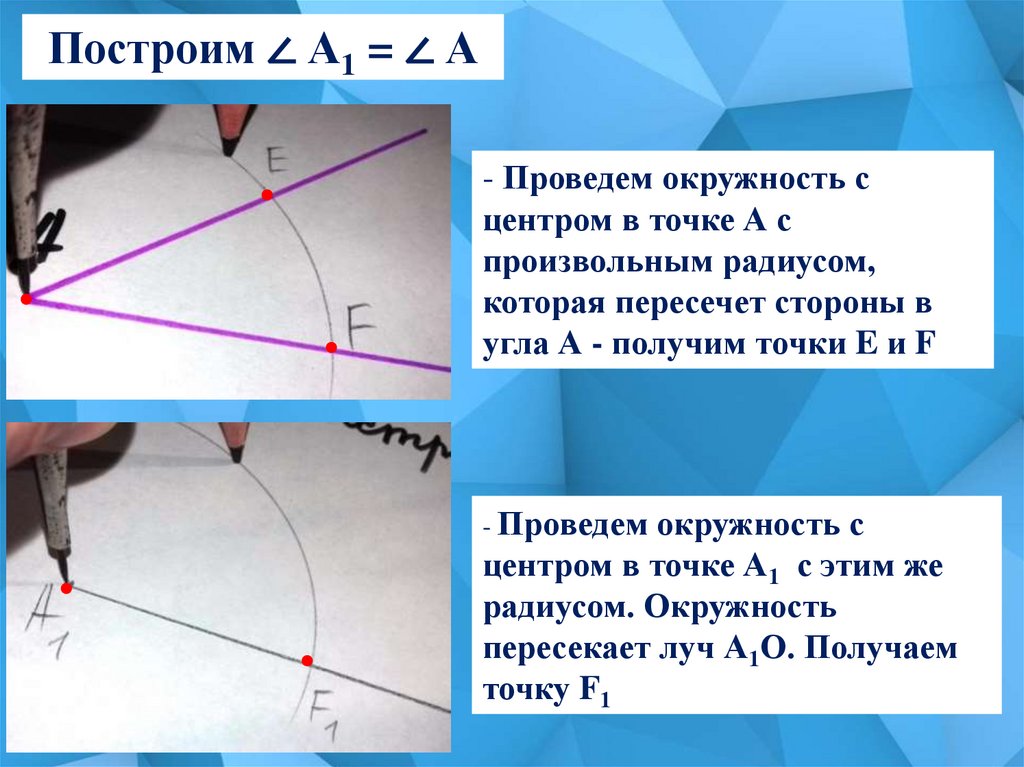
Построим луч А1О

6.

Построим ∠ А1 = ∠ А
- Проведем окружность с
центром в точке А с
произвольным радиусом,
которая пересечет стороны в
угла А - получим точки E и F
- Проведем
окружность с
центром в точке А1 с этим же
радиусом. Окружность
пересекает луч А1О. Получаем
точку F1

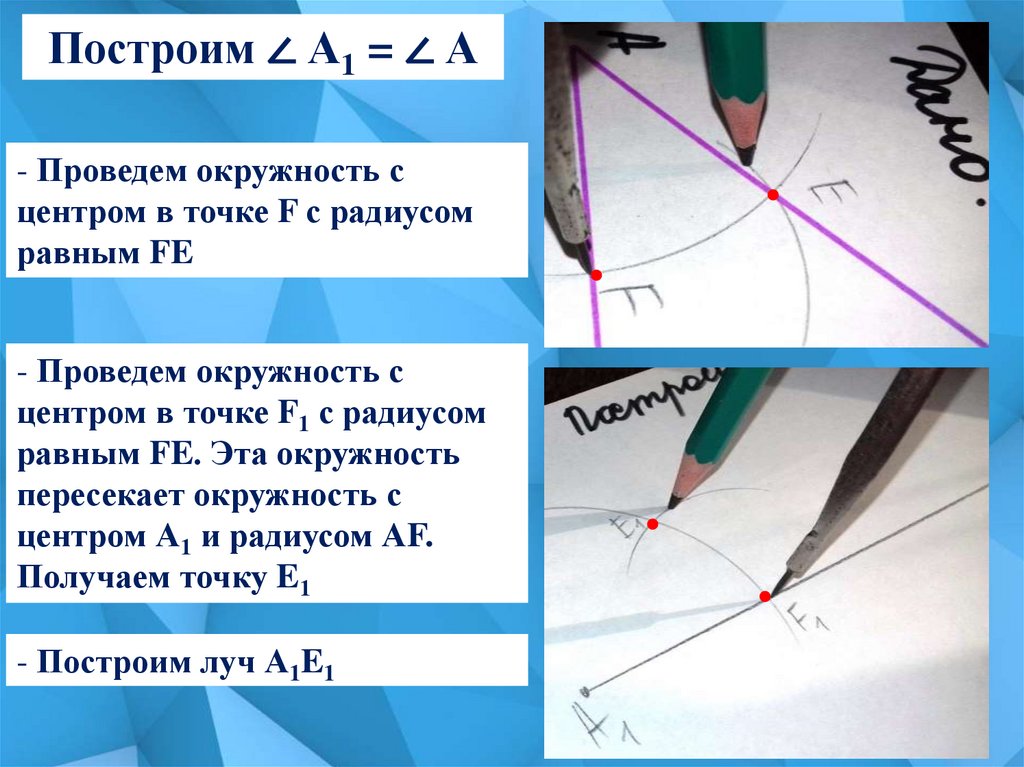
7.

Построим ∠ А1 = ∠ А
- Проведем окружность с
центром в точке F с радиусом
равным FE
- Проведем окружность с
центром в точке F1 с радиусом
равным FE. Эта окружность
пересекает окружность с
центром А1 и радиусом АF.
Получаем точку E1
- Построим луч А1E1

8.

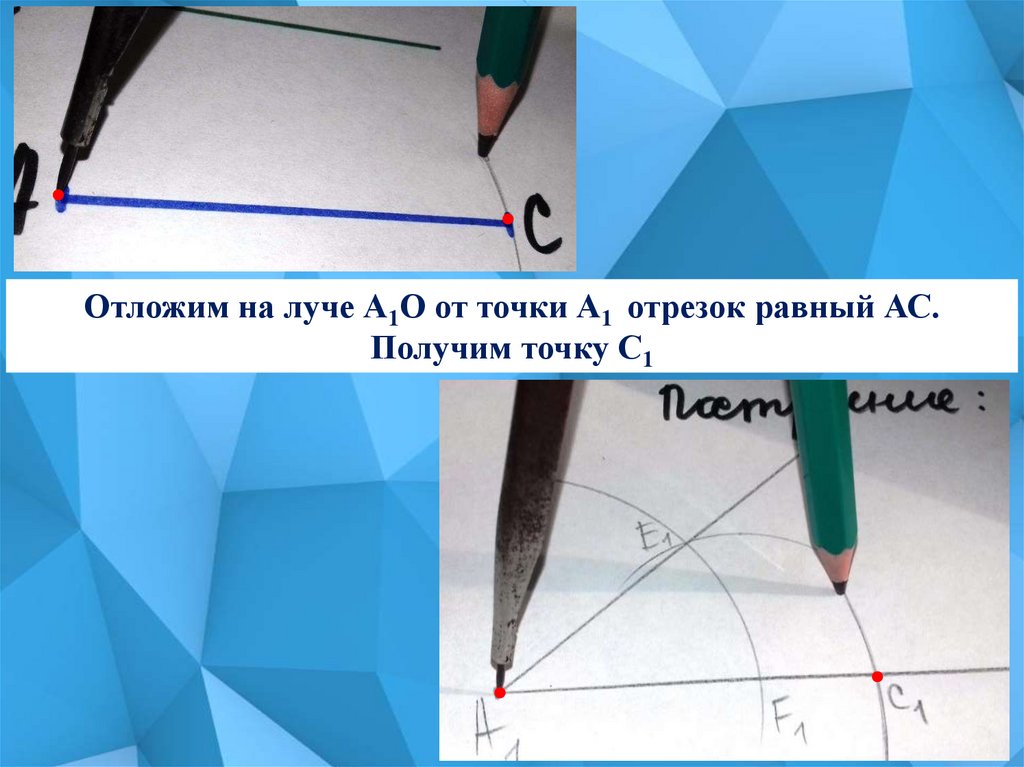
Отложим на луче А1О от точки А1 отрезок равный АС.
Получим точку С1

9.

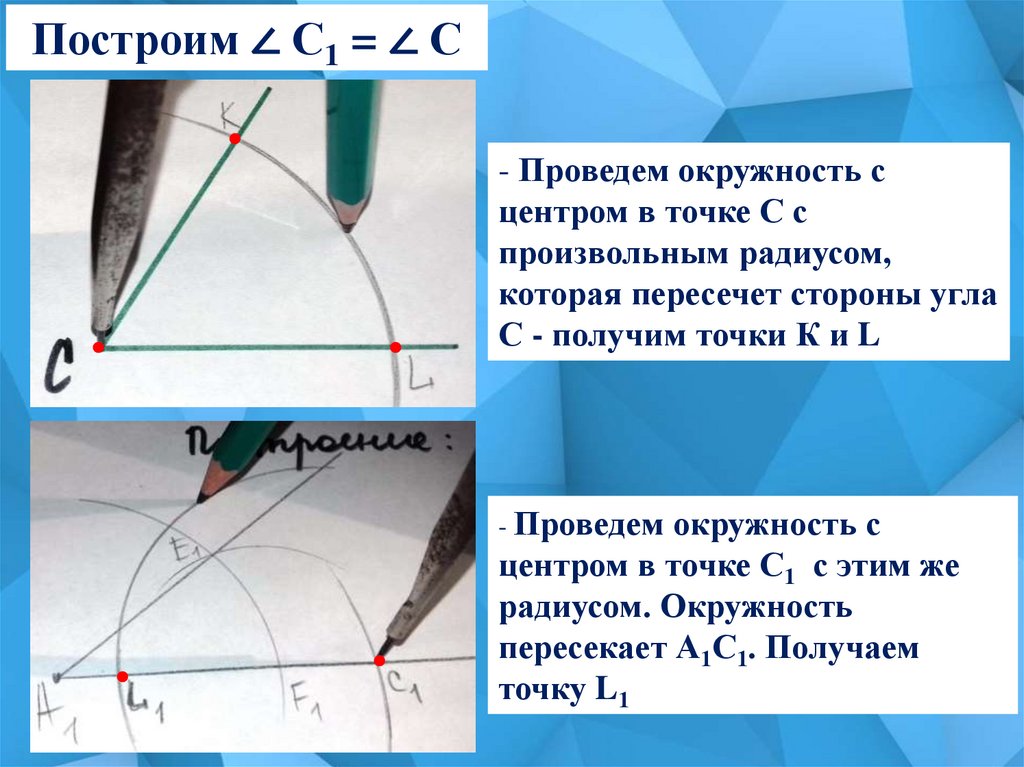
Построим ∠ С1 = ∠ С
- Проведем окружность с
центром в точке С с
произвольным радиусом,
которая пересечет стороны угла
С - получим точки К и L
- Проведем
окружность с
центром в точке С1 с этим же
радиусом. Окружность
пересекает А1С1. Получаем
точку L1

10.

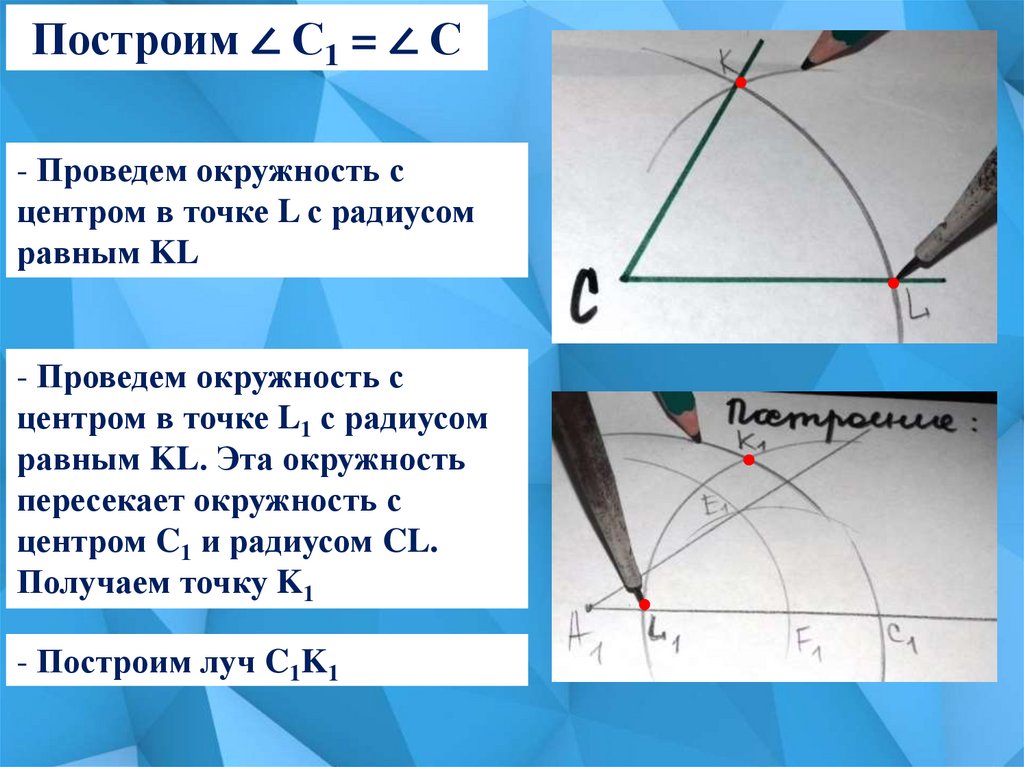
Построим ∠ С1 = ∠ С
- Проведем окружность с
центром в точке L с радиусом
равным KL
- Проведем окружность с
центром в точке L1 с радиусом
равным KL. Эта окружность
пересекает окружность с
центром C1 и радиусом CL.
Получаем точку K1
- Построим луч C1K1

11.

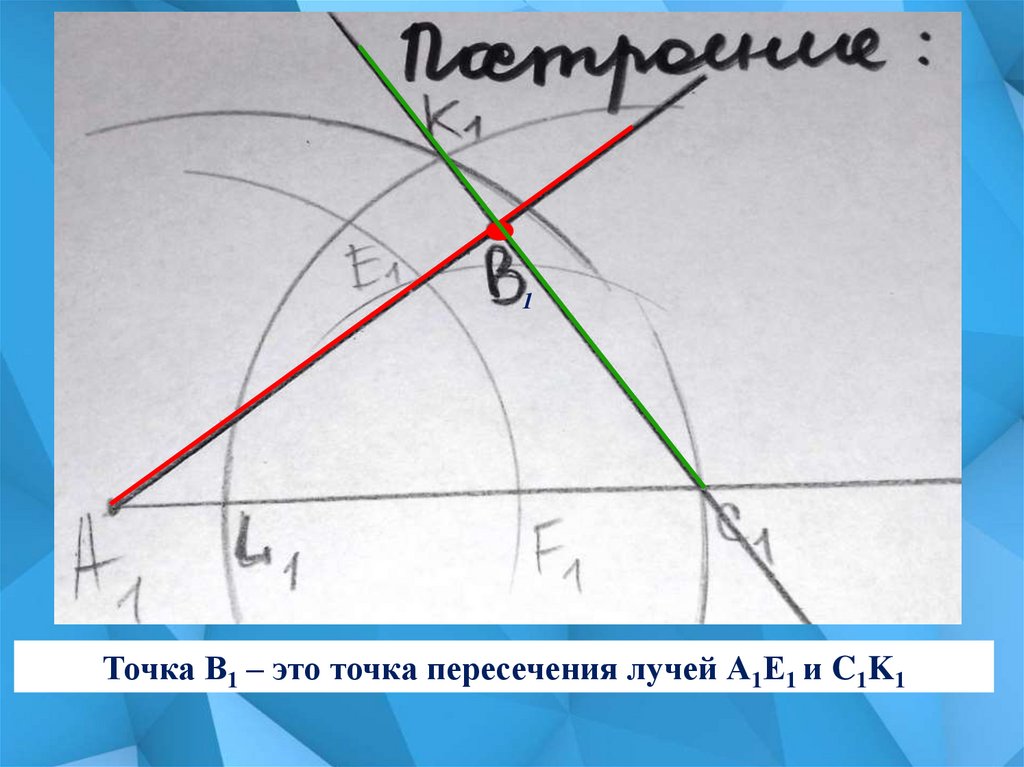
1
Точка В1 – это точка пересечения лучей А1Е1 и C1K1

12.

Согласно признаку равенства треугольников по
стороне и двум прилежащим к ней углам
построенный треугольник равен со всеми
треугольниками, которые имеют данные элементы