Similar presentations:
Построение треугольника по трем элементам
1.
Построение треугольникапо трем элементам
2.
Цель урока:1
рассмотреть задачи на построение
треугольника по трем элементам
2
совершенствовать навыки
решения задач на построение
D
Тип урока: усвоение новых знаний,
учебный и трудовой практикум,
изучение и первичное закрепление
новых знаний.
Метод: наглядно-иллюстративный.
Оборудование: компьютер,
мультимедийный проектор, экран.
3.
Ак
т
у
а
л
и
з
а
ц
и
я
з
н
а
н
и
й
1. Какая фигура называется треугольником?
2. Какие виды треугольников вы знаете?
3. В чем заключается неравенство треугольника?
4. Существуют ли треугольники со сторонами
10 см; 15 см; 30 см?
4.
Перед рассмотрением новой темы повторить построенияциркулем и линейкой
5.
Основные построенияО1
Построение отрезка, равного
данному
О5
О6
Построение прямой. Параллельной
данной прямой и проходящей
через данную точку.
04
Построение перпендикуляра к
данной прямой, проходящей через
данную точку.
6.
О1Построение отрезка, равного
данному
7.
О5Построение перпендикуляра к данной
прямой, проходящей через данную
точку
8.
О6Построение прямой. Параллельной
данной прямой и проходящей через
данную точку.
9.
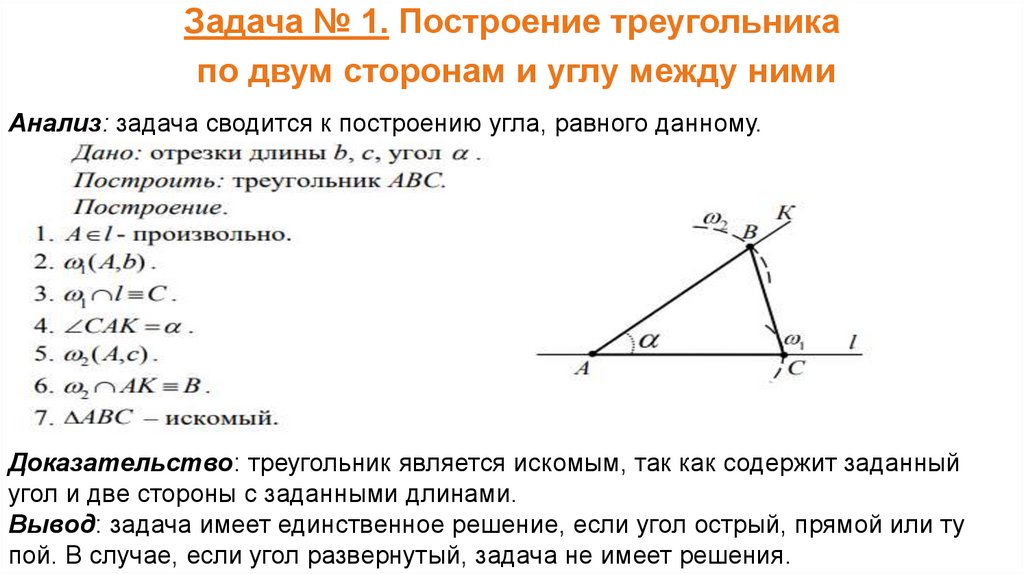
Задача № 1. Построение треугольникапо двум сторонам и углу между ними
Анализ: задача сводится к построению угла, равного данному.
Доказательство: треугольник является искомым, так как содержит заданный
угол и две стороны с заданными длинами.
Вывод: задача имеет единственное решение, если угол острый, прямой или ту
пой. В случае, если угол развернутый, задача не имеет решения.
10.
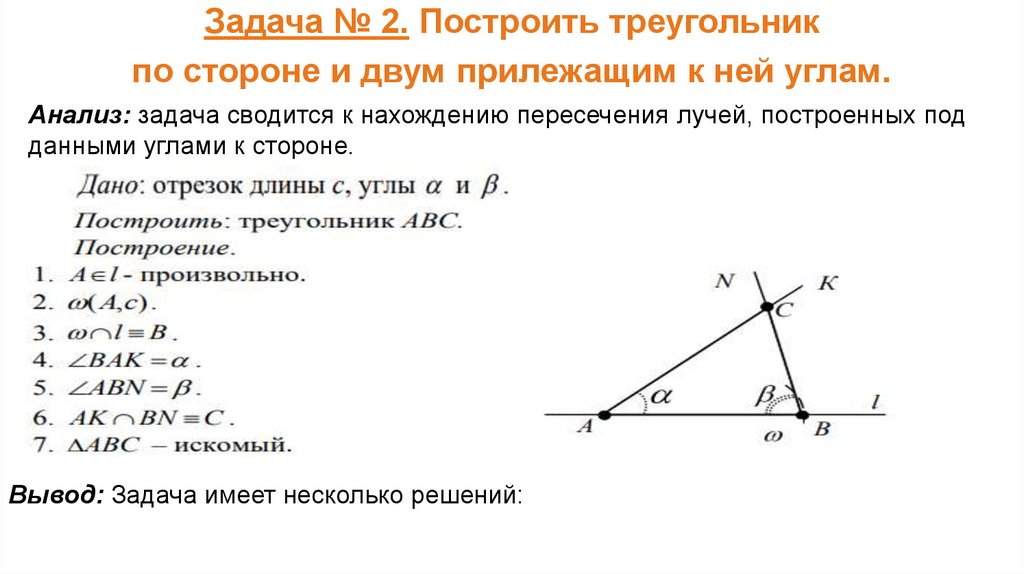
Задача № 2. Построить треугольникпо стороне и двум прилежащим к ней углам.
Анализ: задача сводится к нахождению пересечения лучей, построенных под
данными углами к стороне.
Вывод: Задача имеет несколько решений:
11.
Задача № 3. Построить треугольник по трем сторонам.Анализ: при помощи линейки можно провести луч АВ, при помощи циркуля –
построить на нем отрезок заданной длины.
Вершина С находится на пересечении множеств точек, удаленных на расстояние А
С от точки А (окружности с центром в точке А и радиусом АС), и множества точек, у
даленных на расстояние ВС от точки В ( окружность с центром в точке В радиусом
ВС).
Вывод: треугольник
по трем сторонам
можно построить,
если сумма двух
сторон больше
третьей стороны.











 mathematics
mathematics








