Similar presentations:
Замкнутые системы массового обслуживания
1.
Замкнутые системымассового обслуживания
2.
Состояние Sk системы характеризуется общим числом требований,находящихся на обслуживании и в очереди, равным k.
Для рассматриваемой замкнутой системы, очевидно, k = 0, 1, 2, ... ,
N.
При этом если система находится в состоянии Sk , то число
объектов, находящихся в эксплуатации, равно (N - k).
Если λ- интенсивность потока требований в расчете на одну
машину, то:
3.
• Вероятность k-гo состояния:где ρ=ψ
Величина P0 определяется из условия нормирования
полученных результатов по формулам для Pk , k = 0, 1, 2, ... , N.
Определим следующие вероятностные характеристики системы:
4.
• среднее число требований в очереди на обслуживание:• среднее число требований, находящихся в системе (на
обслуживании и в очереди)
• среднее число механиков (каналов), «простаивающих» из-за
отсутствия работы
5.
• коэффициент простоя обслуживаемого объекта (машины) в очереди• коэффициент использования объектов (машин)
• коэффициент простоя обслуживающих каналов (механиков)
• среднее время ожидания обслуживания (время ожидания
обслуживания в очереди)
6.
Пример 1Пусть для обслуживания десяти персональных компьютеров (ПК) выделено два
инженера одинаковой производительности.
Поток отказов (неисправностей) одного компьютера - пуассоновский с
интенсивностью = 0,2.
Время обслуживания ПК подчиняется показательному закону.
Среднее время обслуживания одного ПК одним инженером составляет: =1,25
час.
Возможны следующие варианты организации обслуживания:
- оба инженера обслуживают все десять компьютеров, так что при отказе ПК
его обслуживает один из свободных инженеров, в этом случае R = 2, N = 10;
- каждый из двух инженеров обслуживает по пять закрепленных за ним ПК. В
этом случае R = 1, N = 5.
Необходимо выбрать наилучший вариант организации обслуживания ПК.
7.
РешениеВычислим параметр обслуживания
Приведенная интенсивность
Вычислим вероятностные характеристики СМО для двух вариантов
организации обслуживания ПК.
Вариант 1
1. Определим вероятности состояний системы:
8.
9.
10.
11.
• Определим среднее число компьютеров в очереди на обслуживание:• Определим среднее число ПК, находящихся в системе (на
обслуживании и в очереди):
12.
• Определим среднее число инженеров, простаивающих из-за отсутствияработы:
• Коэффициент простоя персонального компьютера в очереди
следующий:
• Коэффициент использования компьютеров определяется по формуле:
13.
• Коэффициент простоя обслуживающих инженеров рассчитывается так:• Среднее время ожидания ПК обслуживания
Вариант 2
Определим вероятности состояний системы:
14.
15.
• Откуда P0 = 0,199.• Тогда
16.
• Среднее число компьютеров в очереди на обслуживание таково:• Среднее число компьютеров, находящихся на обслуживании и в
очереди рассчитывается так:
• Среднее число инженеров, простаивающих из-за отсутствия
работы:
17.
• Коэффициент простоя персонального компьютера в очереди:• Коэффициент использования компьютеров:
• Коэффициент простоя обслуживающих инженеров:
• Среднее время ожидания ПК обслуживания:
18.
Таким образом, в варианте 1 каждый компьютер стоит в очереди вожидании начала его обслуживания приблизительно 0,142 части
рабочего времени, что меньше этого показателя при варианте 2
организации работ.
В варианте 1 вероятность того, что ПК и любой момент времени будет
работать выше, чем в варианте 2.
Очевидно, вариант 1 организации работ по обслуживанию ПК
эффективнее, чем вариант 2.
19.
n- канальная СМО замкнутого типа с mисточниками заявок
ПРИМЕР 1
Пять ткачих обслуживают 20 ткацких станков.
Средняя продолжительность бесперебойной работы
станка-30 минут, устранение неисправности
(обрывания нити) занимает в среднем 1,5 минуты.
Найти характеристики СМО.
20.
РЕШЕНИЕИмеем:
n = 5,
m = 20,
λ = 1/30 [мин]-1,
μ = 2/3 [мин]-1,
ρ = λ/μ = 1/20.
Поскольку ρ ≠ 1(m - n), то р0 находим по формуле
21.
Финальные состояния-вероятность того, что заняты все ткачихи
вероятность того, что заняты все ткачихи
22.
Вероятность образования очереди находим по формулеСреднее число ткачих, занятых обслуживанием станков находим по
формуле
23.
Среднее число станков, находящихся в очереди, находимпо формуле
Полное число неработающих станков равно
24.
ПРИМЕР 2На промышленном предприятии решается вопрос о том, сколько
потребуется механиков для работы в ремонтном цехе.
Пусть предприятие имеет 10 машин, требующих ремонта с учетом
числа ремонтирующихся.
Отказы машин происходят с частотой λ=10 отк/час.
Для устранения неисправности механику требуется в среднем t=3 мин.
Распределение моментов возникновения отказов является
пуассоновским, а продолжительность выполнения ремонтных работ
распределена экспоненциально.
Возможно организовать 4 или 6 рабочих мест в цехе для механиков
предприятия.
Необходимо выбрать наиболее эффективный вариант
обеспечения ремонтного цеха рабочими местами для механиков.
25.
РЕШЕНИЕОпределим исходные данные.
Интенсивность входящего потока λ=10
отк/час=10/60=1/6 в минуту.
Интенсивность потока обслуживания µ=1/t=1/3.
N=10.
Рассмотрим вероятность отказа в обслуживании
для n=4 и n=6 рабочих мест в цехе для механиков (n –
число каналов обслуживания).
26.
n=427.
n=6Таким образом, вероятность отказа в обслуживании
практически равна нулю во втором случае (6 рабочих),
поэтому если это принципиально, то лучше иметь 6 рабочих.
28.
Самостоятельно. Вариант 1В вычислительном центре работает 9 персональных компьютеров (ПК).
Простейший поток неисправностей имеет интенсивность 0,3 отказа в день.
Среднее время устранения одной неисправности одним инженером равно 1,5
час.
Компьютеры обслуживают три инженера с одинаковой производительностью.
Все потоки событий простейшие.
Возможны следующие варианты организации обслуживания ПК:
- три инженера обслуживают все 9 компьютеров, так, что при отказе ПК его
обслуживает один из свободных инженеров, в этом случае R = 3; N = 9;
- каждый из трех инженеров обслуживает по три закрепленных за ним ПК. В
этом случае R = 1; N = 3.
Необходимо выбрать наилучший вариант организации обслуживания ПК.
29.
Задача 2.Малое транспортное предприятие эксплуатирует десять моделей
автомобилей одной марки.
Простейший поток отказов автомобилей имеет интенсивность = 0,25 отказа в
день.
Среднее время устранения одного отказа автомобиля одним механиком
равно 2 час.
Все потоки событий простейшие.
Возможны два варианта обслуживания:
- все автомобили обслуживают два механика с одинаковой
производительностью;
- все автомобили предприятия обслуживают три механика с одинаковой
производительностью.
Необходимо выбрать наилучший вариант организации обслуживания
автомобилей.
30.
Самостоятельные задачи:Задача 1.
На промышленном предприятии решается вопрос о том, сколько
потребуется механиков для работы в ремонтном цехе.
Пусть предприятие имеет 10 машин, требующих ремонта с учетом числа
ремонтирующихся.
Отказы машин происходят с частотой = 10 отк/час.
Для устранения неисправности механику требуется в среднем = 3 мин.
Распределение моментов возникновения отказов является пуассоновским,
а продолжительность выполнения ремонтных работ распределена
экспоненциально.
Возможно организовать 4 или 6 рабочих мест в цехе для механиков
предприятия.
Необходимо выбрать наиболее эффективный вариант обеспечения
ремонтного цеха рабочими местами для механиков.
31.
Задача 2.Малое транспортное предприятие эксплуатирует десять моделей
автомобилей одной марки.
Простейший поток отказов автомобилей имеет интенсивность = 0,25 отказа в
день.
Среднее время устранения одного отказа автомобиля одним механиком
равно 2 час.
Все потоки событий простейшие.
Возможны два варианта обслуживания:
- все автомобили обслуживают два механика с одинаковой
производительностью;
- все автомобили предприятия обслуживают три механика с одинаковой
производительностью.
Необходимо выбрать наилучший вариант организации обслуживания
автомобилей.
32.
Самостоятельно. Вариант 1В вычислительном центре работает 9 персональных компьютеров (ПК).
Простейший поток неисправностей имеет интенсивность 0,3 отказа в день.
Среднее время устранения одной неисправности одним инженером равно 1,5
час.
Компьютеры обслуживают три инженера с одинаковой производительностью.
Все потоки событий простейшие.
Возможны следующие варианты организации обслуживания ПК:
- три инженера обслуживают все 9 компьютеров, так, что при отказе ПК его
обслуживает один из свободных инженеров, в этом случае R = 3; N = 9;
- каждый из трех инженеров обслуживает по три закрепленных за ним ПК. В
этом случае R = 1; N = 3.
Необходимо выбрать наилучший вариант организации обслуживания ПК.
33.
ПРИМЕР.В распоряжении магазина находится 10 грузовиков. Грузовики прибывают в магазин в случайном
порядке в течение дня для погрузки-разгрузки. Каждый грузовик прибывает на обслуживание дважды за
8-часовой рабочий день. Средняя скорость обслуживания — 4 грузовика в час. Поток грузовиков
описывается пуассоновским распределением, время обслуживания — экспоненциальным. Определите:
Вероятность того, что ни один грузовик не ожидает погрузки-разгрузки;
Среднее число грузовиков в очереди;
Среднее число грузовиков у магазина (грузовики в очереди и на погрузке-разгрузке);
Среднее время ожидания в очереди.
Вопрос: Каковы часовые издержки по функционированию системы, если в час
издержки на каждый грузовик равны 50 долл., а на работы с грузовиками — 30 долл.?
Вероятность того, что ни один грузовик не ожидает погрузки-разгрузки, Р0 = 0,44;
• Среднее число грузовиков в очереди Lq = 0,490;
• Среднее число грузовиков у магазина LS = 1,049;
• Среднее время ожидания Wq = 0,219 ч = 13 мин;
• Издержки по функционированию системы равны 54,48 долл. в час.
34.
Задача.Рабочий обслуживает 4 станка, каждый станок
отказывает с интенсивностью 0,5 отказа в час.
Среднее время ремонта одного станка 0,8 ч.
Все потоки событий простейшие.
Определите основные показатели, характеризующие
систему массового обслуживания.
35.
Задача.Двое рабочих обслуживают 6 станков.
Станок требует наладки в среднем каждые полчаса. Наладка
занимает у рабочего в среднем 10 мин.
Все потоки событий простейшие.
Определите характеристики системы массового обслуживания.
Установите, улучшатся ли характеристики системы массового
обслуживания, если рабочие будут налаживать станки
совместно, тратя вдвоем на наладку в среднем 5 мин.
36.
ЗадачаНа АТС поступают заявки на междугородние
переговоры.
В среднем за 1 ч поступает 13 заявок.
Приведите аргументы против того, что поток заявок на
телефонную станцию является ординарным.
Найдите среднее число заявок, поступающих за сутки.
На телефонной станции появляются сбои в работе,
если за полчаса на нее поступит более 50 заявок.
Найдите вероятность сбоя станции.
37.
Задача.Среднее число покупателей, поступающих на
узел расчета в магазине самообслуживания, 100
человек в час.
Кассир может обслуживать 60 человек в час.
Определите, какое число кассиров необходимо
для того, чтобы вероятность появления очереди
не превысила 0,60.







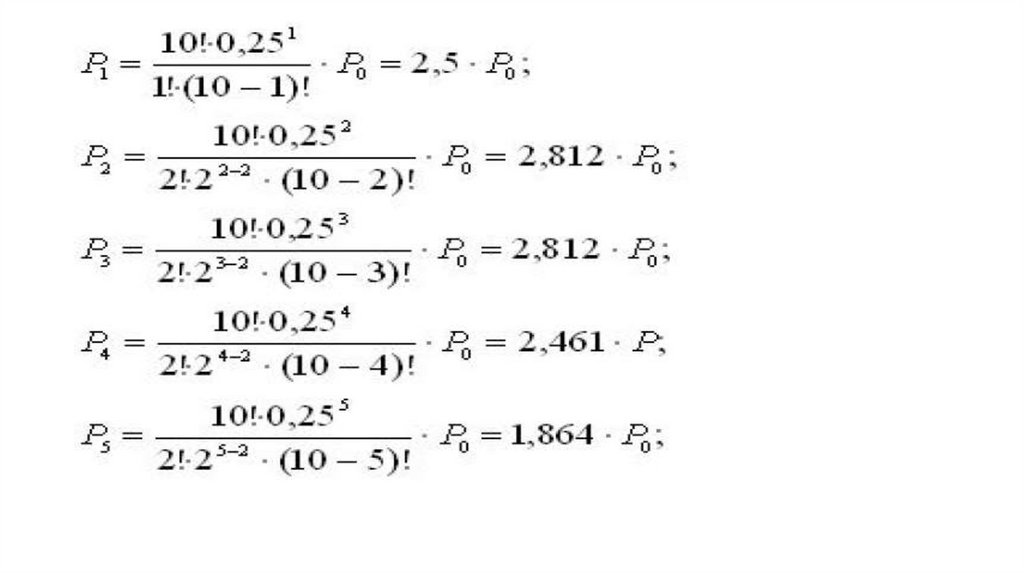
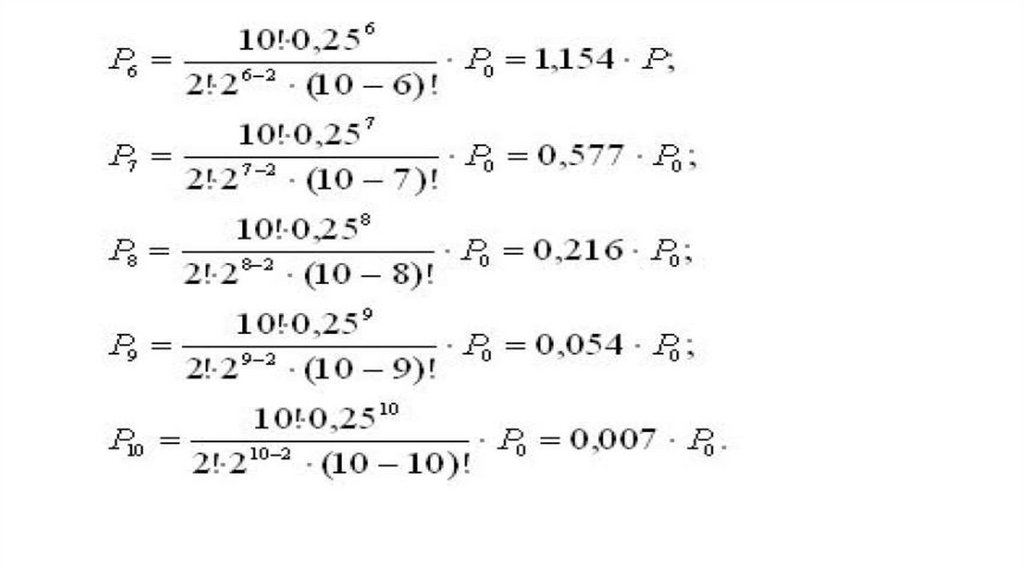




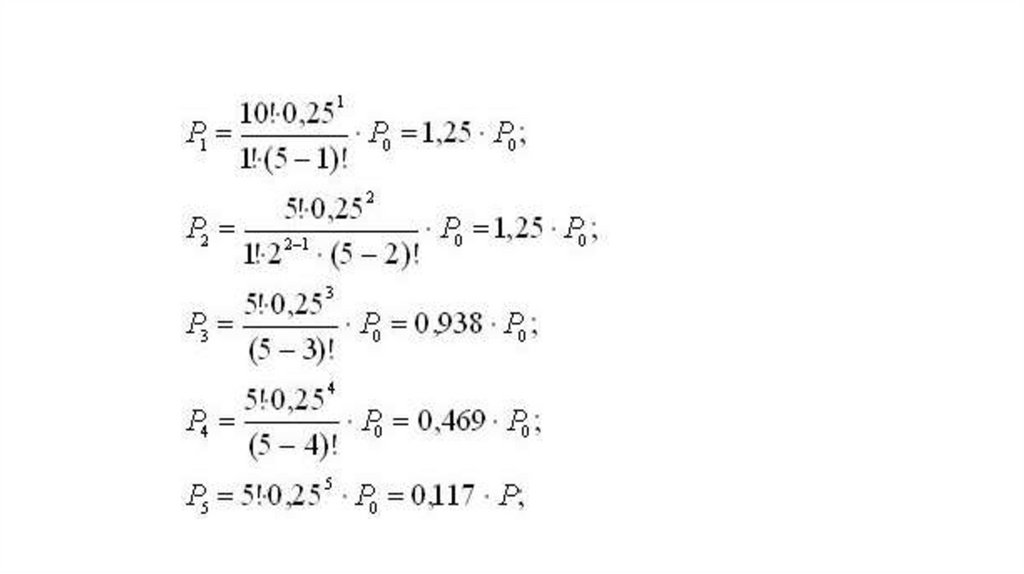











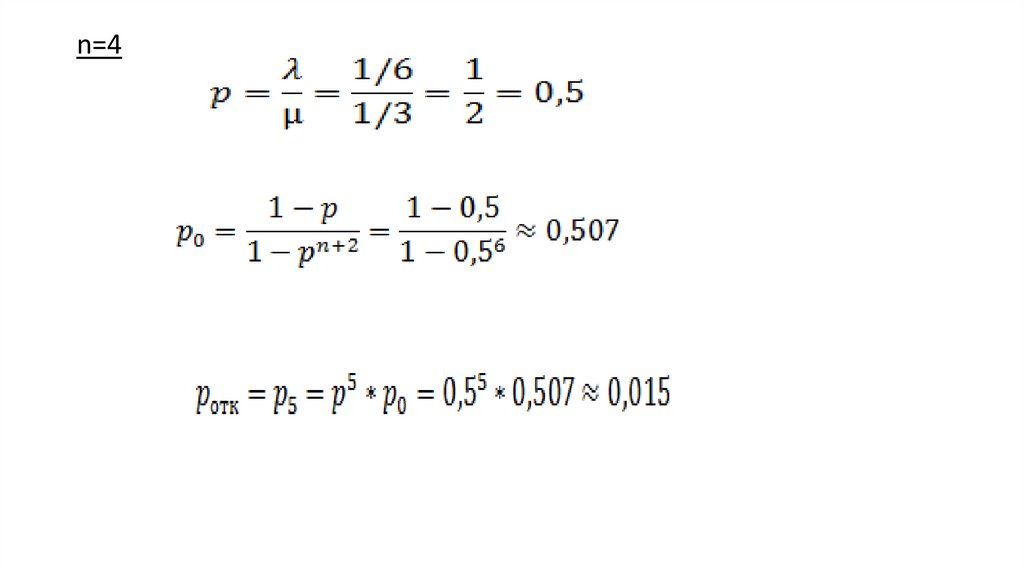











 mathematics
mathematics informatics
informatics








