Similar presentations:
Способы решений тригонометрических уравнений. Метод введения новой перменной
1. Способы решений тригонометрических уравнений.
Метод введения новой перменной2.
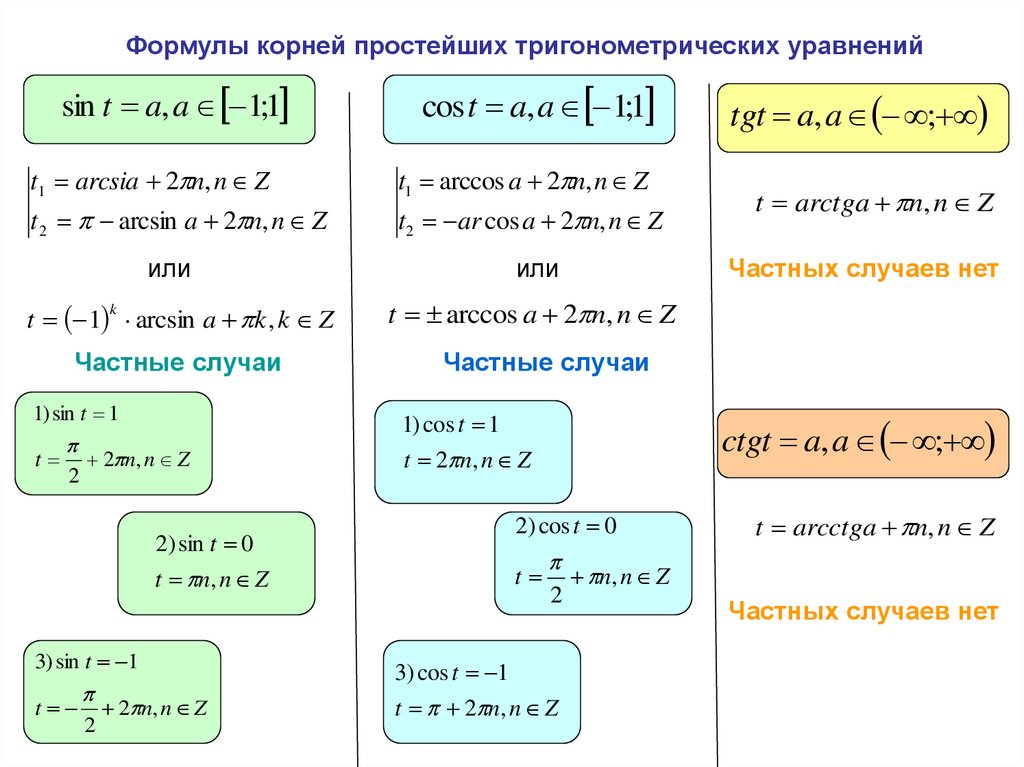
Формулы корней простейших тригонометрических уравненийsin t a, a 1;1
cos t a, a 1;1
t1 arcsia 2 n, n Z
t1 arccos a 2 n, n Z
t 2 arcsin a 2 n, n Z
t2 ar cos a 2 n, n Z
или
t 1 arcsin a k , k Z
k
Частные случаи
1) sin t 1
t
2
или
t arccos a 2 n, n Z
Частные случаи
2) cos t 0
t
t n, n Z
t
2
ctgt a,a ;
t 2 n, n Z
2) sin t 0
3) sin t 1
2 n, n Z
t arctga n, n Z
Частных случаев нет
1) cos t 1
2 n, n Z
tgt a,a ;
2
3) cos t 1
t 2 n, n Z
t arcctga n, n Z
n, n Z
Частных случаев нет
3.
Работа над ошибками в домашнем задании2
sin 2 x
2
Применяем
развернутую формулу
t arcsia 2 n, n Z
1
2
2 x1 arcsin
2t 2 n , n arcsin
Z
a 2 n, n Z
2
2
2 x2 arcsin
2 n, n Z
2
2 x1
Если применить
вторую формулу, то:
2 x 1 arcsin
2
k , k Z
2
k
2 x 1
k
x 1
k
8
4
k , k Z
k
2
,k Z
4
2 n, n Z
2 x2
2 x1
4
2 n, n Z
2 n, n Z
4
3
2 x2
2 n, n Z
4
Ответ:
8
n;
n, n Z
8
3
x2
n, n Z
8
x1
3
n, n Z
8
4.
x1
cos
3
2
Применим формулу
t arccos a 2 n, n Z
x
1
arccos 2 n, n Z
3
2
вспоминаем,
x
1Теперь
arccos что
2 n, n Z
3
2 ar cos a arccos a
x
2 n, n Z
3
3
x
2
2 n, n Z
3
3
x 2 6 n, n Z
Ответ:
2 6 n, n Z
5.
x2
sin
3
2
Применяем формулу
t 1 arcsin a k , k Z
k
x
2
k
k , k Z
1 arcsin
3
2
x
2
k
k , k Теперь
1 arcsin
Z
вспоминаем,
3
2
что
x
k
1 k , k Z
arcsin a arcsin a
3
4
x
k
1 1 k , k Z
3
4
x
k 1
1 k , k Z
3
4
sin
x 1
k 1
x
2
3
2
x1
2
arcsin
2 n, n Z
3
2
x1
2 n, n Z
3
4
3
x1
6 n, n Z
4
или
x2
2
arcsin
2 n, n Z
3
2
xx22
3
2 n2,
nn , nZ Z
33
4 4
9
x2
6 n, n Z
4
3
3 k , k Z
4
6.
Все шаги выполненыверно!
НО!!!!
Формула корней уравнения
tgt a
имеет вид
t arctga n, n Z
Верный ответ:
x 2 n, n Z
7.
Метод замены переменнойЭтот метод хорошо известен, он часто
применяется при решении
различных уравнений. Покажем на
примерах его применение при
решении тригонометрических
уравнений
8.
t2Решим уравнение:
t
4 sin 2 x 11sin x 3 0
Пусть sin x t , t 1;1
Решение:
4t 2 11t 3 0
3 1;1
t1 3
1
t2
4
sin x
Согласно замене:
1
4
x 1 arcsin
k
Ответ:
1 k arcsin 1 k , k Z
4
1
k , k Z
4
9.
Решим уравнение:Решение:
cos x sin x cos x 0
2
2
Воспользуемся
тригонометрической
единицей
sin 2 t cos 2 t 1
cos 2 x 1 cos 2 x cos x 0
cos x 1 cos x cos x 0
2
2
отсюда
sin 2 t 1 cos 2 t
t
t2
2 cos 2 x cos x 1 0
Пусть
cos x t
t 1;1
2t 2 t 1 0
Частный случай
t1 1
cos x 1
x 2 n, n Z
Ответ:
2 n;
1
t2
2
или
Согласно замене:
1
cos x
2
1
x arccos 2 n, n Z
2
2
x
2 n, n Z
3
2
2 n, n Z
3
10.
Решить уравнение 2tg2 x + 3tg x - 2 = 0.Решение.
Введем новую переменную t = tg x, тогда уравнение примет вид:
2t2 + 3t - 2 = 0.
Далее получаем:
t1 = -2;
t2 = 1/2.
Возвращаясь к переменной х получаем два уравнения: tg x = -2 или tg x =1/2.
Из первого уравнения находим: x = - arctg 2 + П n.
Из второго уравнения находим: x = arctg 1/2 + П n.
Ответ:x = - arctg 2 + П n.
x = arctg 1/2 + П n.
11.
Решим уравнение:Решение:
tg
Пусть tg
tg
x
x
3ctg 4
2
2
tgt ctgt 1
x
1
3
4
x
2
tg
2
x
t
2
Тогда
3
t 4 0
t
t 4t 3
0
t
t 2 4t 3 0, t 0
t1 1
t2 3
ctgt
t-любое число!
1
t 3 4
t
2
Воспользуемся тем,
что
1
tgt
Согласно замене:
tg
x
1
2
или
x
n, n Z
2 4
x
2
Ответ:
2 n, n Z
2
2 n;
tg
x
3
2
x
arctg 3 n, n Z
2
x 2arctg 3 2 n, n Z
2arctg 3 2 n, n Z










 mathematics
mathematics








