Перпендикулярные прямые в пространстве

1.

2.

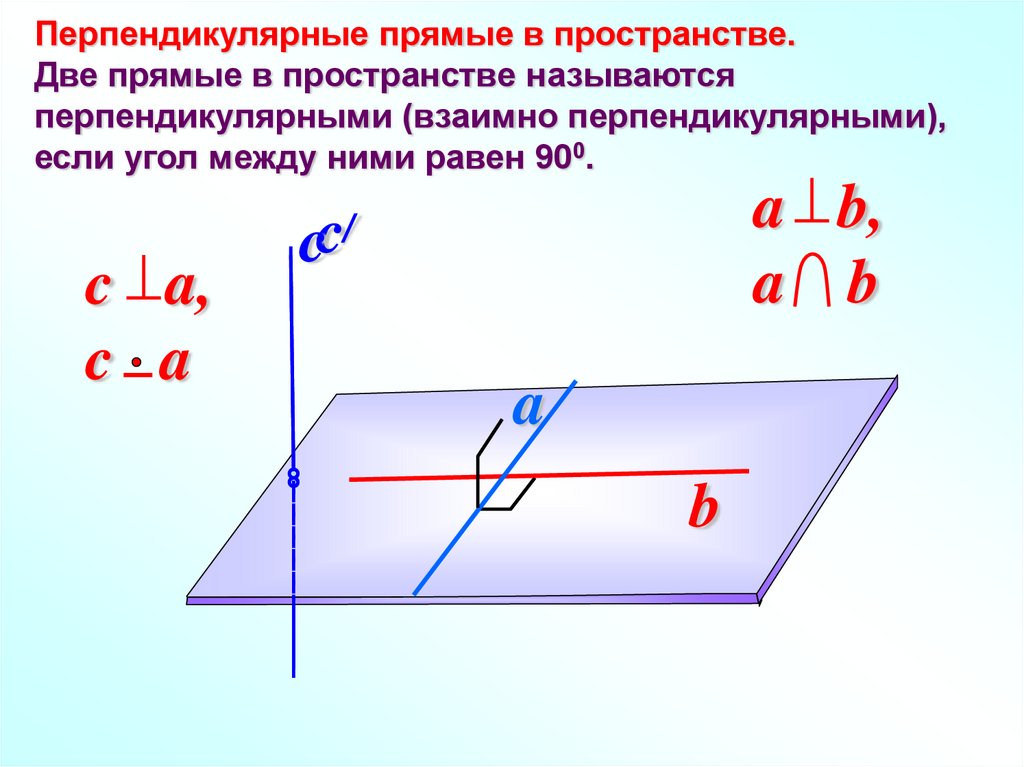
Перпендикулярные прямые в пространстве.
Две прямые в пространстве называются
перпендикулярными (взаимно перпендикулярными),
если угол между ними равен 900.
c a,
c a
a b,
a b
/
c
c
a
b

3.

Лемма: Если одна из двух параллельных прямых
перпендикулярна к третьей прямой, то и другая
прямая перпендикулярна к этой прямой.
Дано: a║b; a┴с
a
Доказать: b┴c
Доказательство:
b
c
M
C
A
Проведем CM║c, MA║a.
Так как a┴с, то └AMC=90
a║b (по условию)
MA║a.(по построению) =>
}
MA║b, MC║c
MA┴MC
}
=>
b┴c

4.

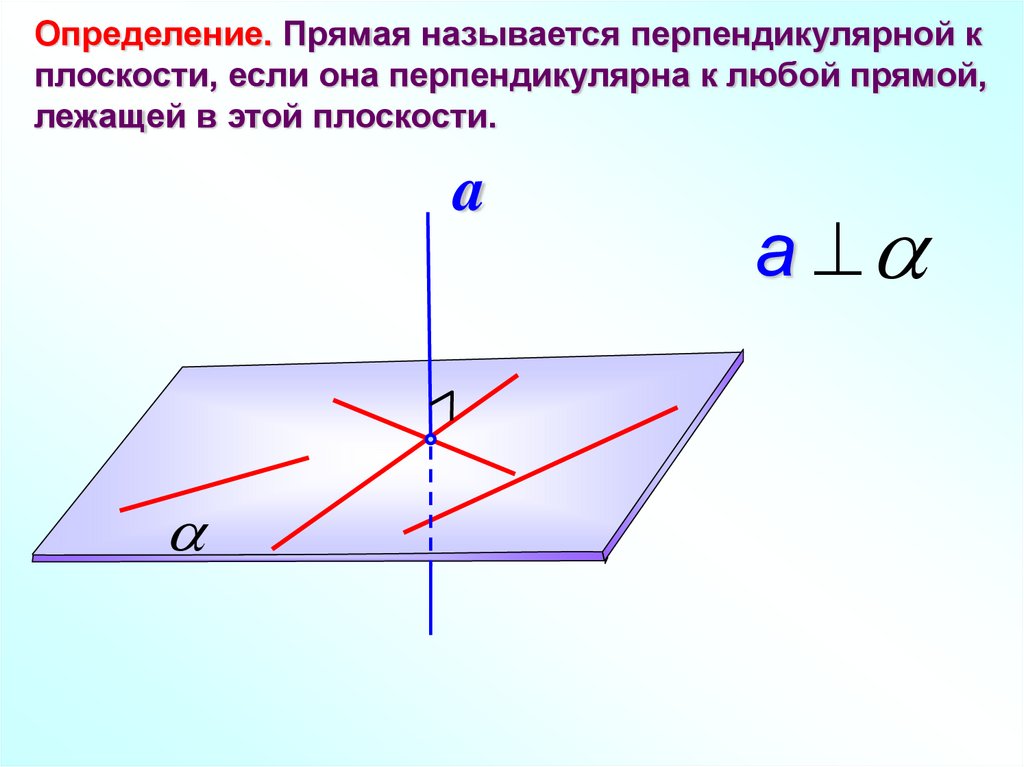
Определение. Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
a

5.

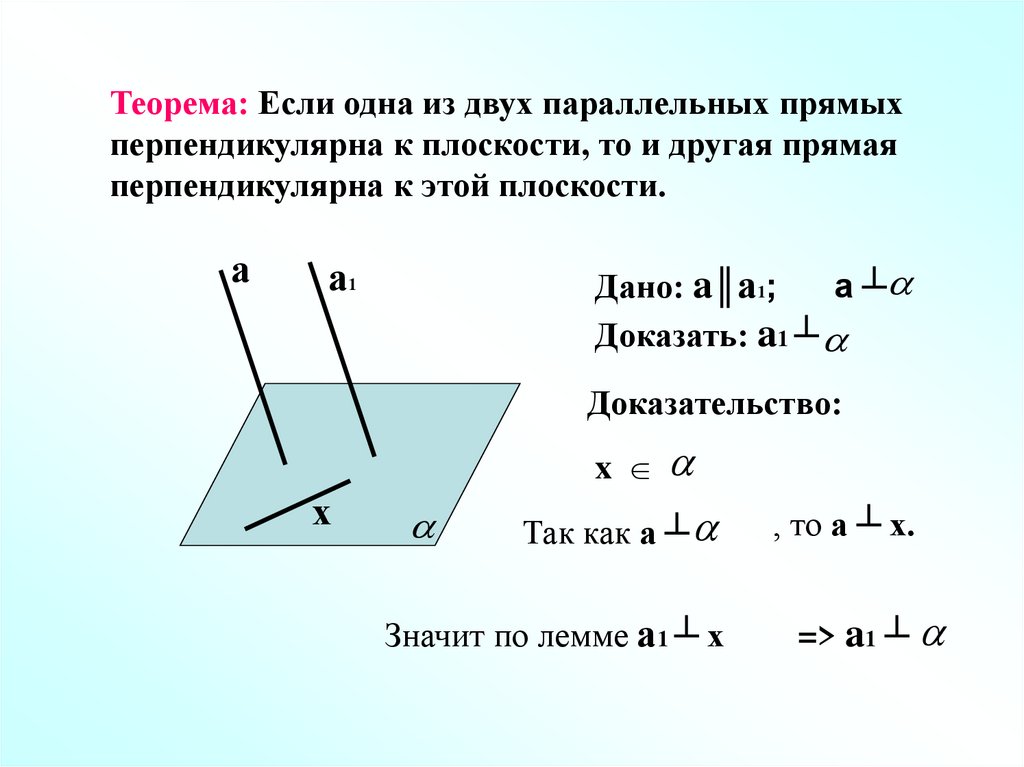
Теорема: Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая прямая
перпендикулярна к этой плоскости.
а
а1
Дано: a║а1;
a ┴
Доказать: a1 ┴
Доказательство:
x
х
Так как a ┴
Значит по лемме а1 ┴ х
, то a ┴ х.
=> a1 ┴

6.

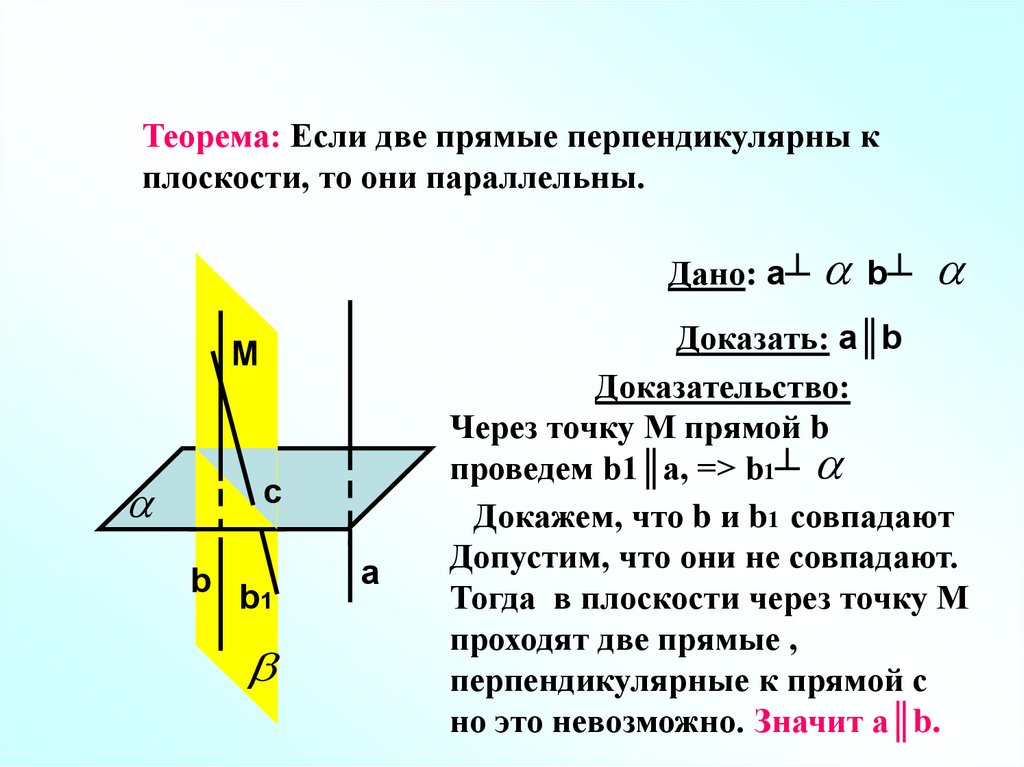
Теорема: Если две прямые перпендикулярны к
плоскости, то они параллельны.
Дано: a┴ b┴
M
c
b b1
a
Доказать: a║b
Доказательство:
Через точку М прямой b
проведем b1║a, => b1┴
Докажем, что b и b1 совпадают
Допустим, что они не совпадают.
Тогда в плоскости через точку М
проходят две прямые ,
перпендикулярные к прямой с
но это невозможно. Значит а║b.

7.

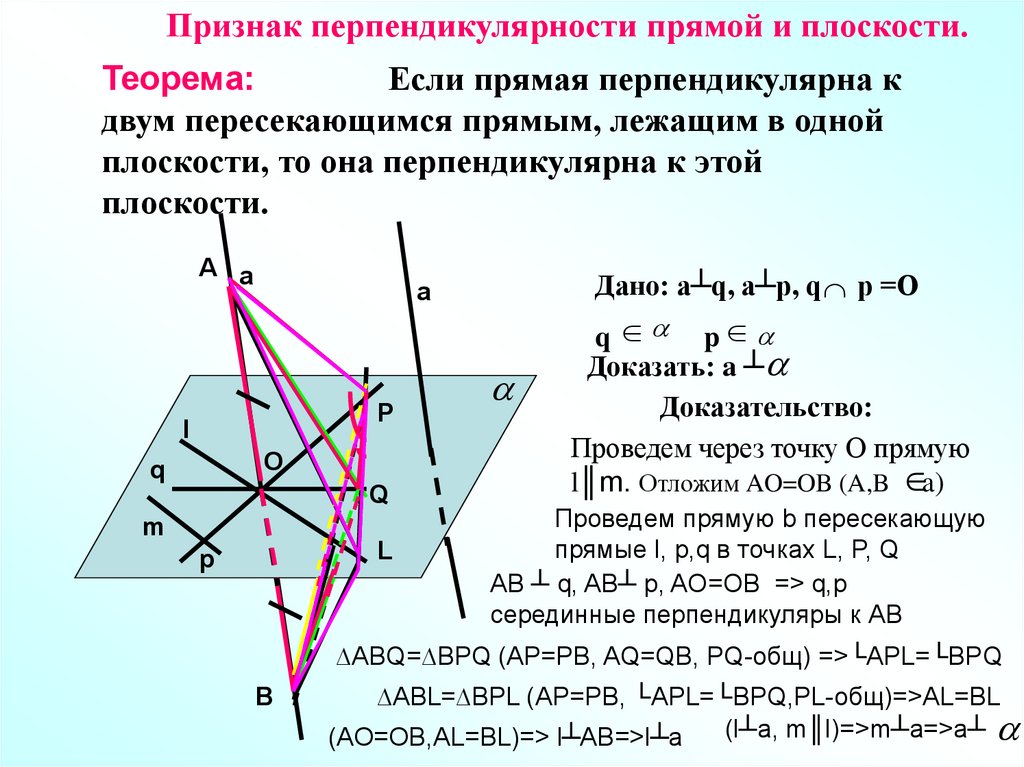
Признак перпендикулярности прямой и плоскости.
Теорема:
Если прямая перпендикулярна к
двум пересекающимся прямым, лежащим в одной
плоскости, то она перпендикулярна к этой
плоскости.
A a
a
P
l
O
q
Q
m
L
p
Дано: a┴q, a┴p, q p =O
q p
Доказать: a ┴
Доказательство:
Проведем через точку О прямую
l║m. Отложим AO=OB (A,B a)
Проведем прямую b пересекающую
прямые l, p,q в точках L, P, Q
AB ┴ q, AB┴ p, AO=OB => q,p
серединные перпендикуляры к АВ
∆ABQ=∆BPQ (AP=PB, AQ=QB, PQ-общ) =>└APL=└BPQ
B
∆ABL=∆BPL (AP=PB, └APL=└BPQ,PL-общ)=>AL=BL
(l┴a, m║l)=>m┴a=>a┴
(AO=OB,AL=BL)=> l┴AB=>l┴a

8.

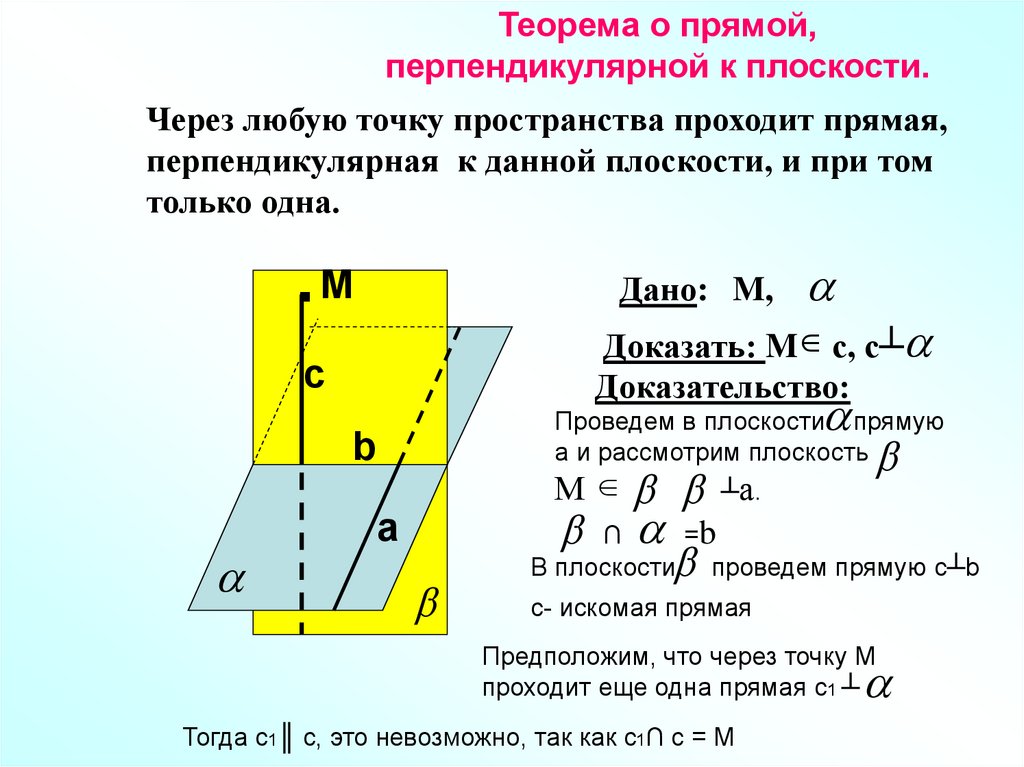
Теорема о прямой,
перпендикулярной к плоскости.
Через любую точку пространства проходит прямая,
перпендикулярная к данной плоскости, и при том
только одна.
.M
Дано: M,
Доказать: M с, c┴
Доказательство:
c
Проведем в плоскости прямую
а и рассмотрим плоскость
b
М
a
┴а.
∩ =b
В плоскости проведем прямую с┴b
с- искомая прямая
Предположим, что через точку М
проходит еще одна прямая с1 ┴
Тогда с1║ с, это невозможно, так как с1∩ с = М