Similar presentations:
Производная в заданиях ЕГЭ (11 класс)
1.
Производная в заданияхЕГЭ
Открытый урок в 11 классе.
Учитель математики МБОУ СОШ№21
Скороходова Н.Ф.
2.
Цель урока: формирование практических навыковрешения задач по теме «Производная»
Задачи урока:
• Повторить теоретические знания по теме
«Производная функции и ее
геометрический смысл».
• Научиться решать задачи типа №14
(базовый уровень) из открытого банка
заданий для подготовки к ЕГЭ.
3.
«Уча других, мы учимся сами»Сенека (римский философ)
Хочешь научиться сам –
начни учить других!
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
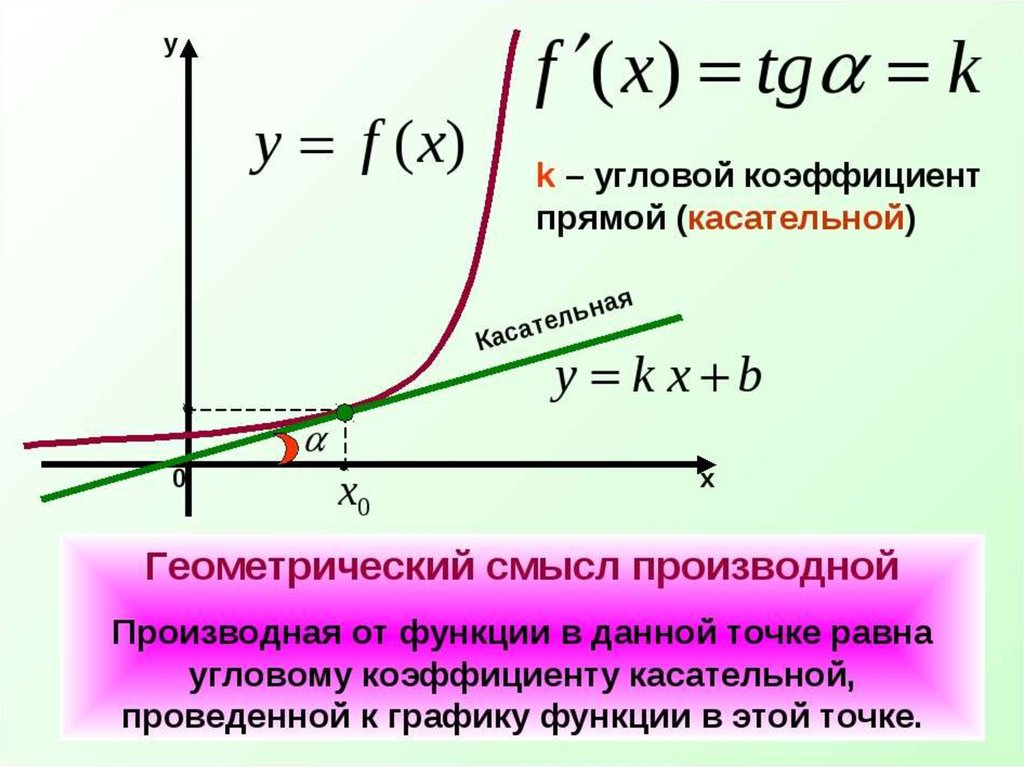
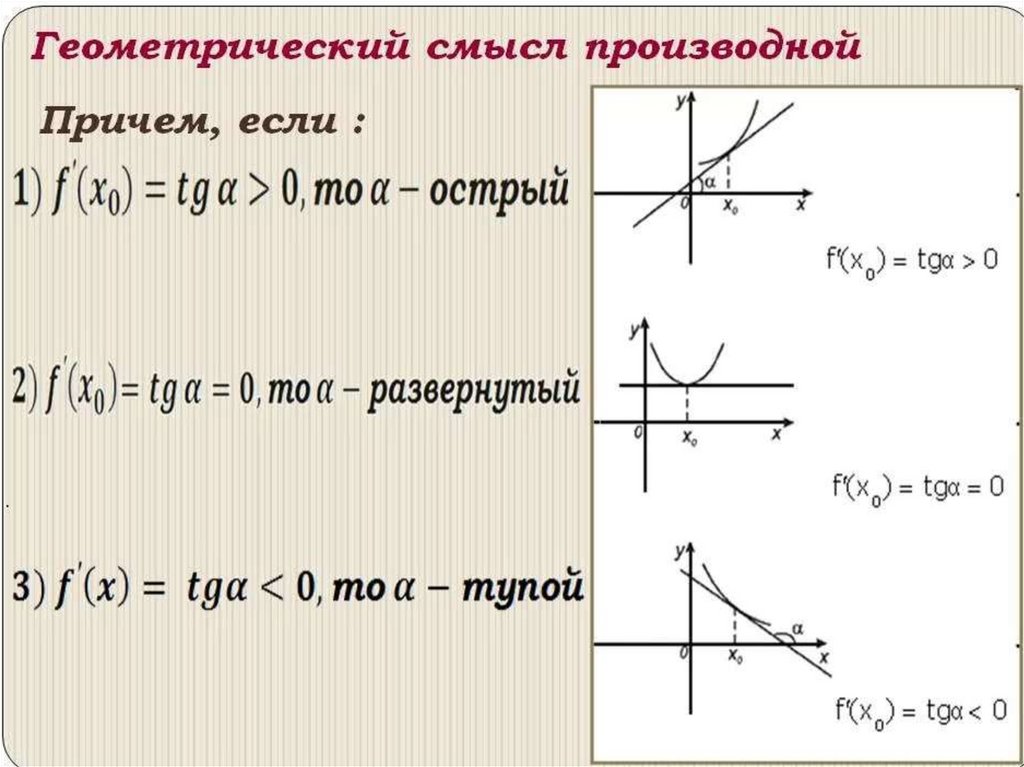
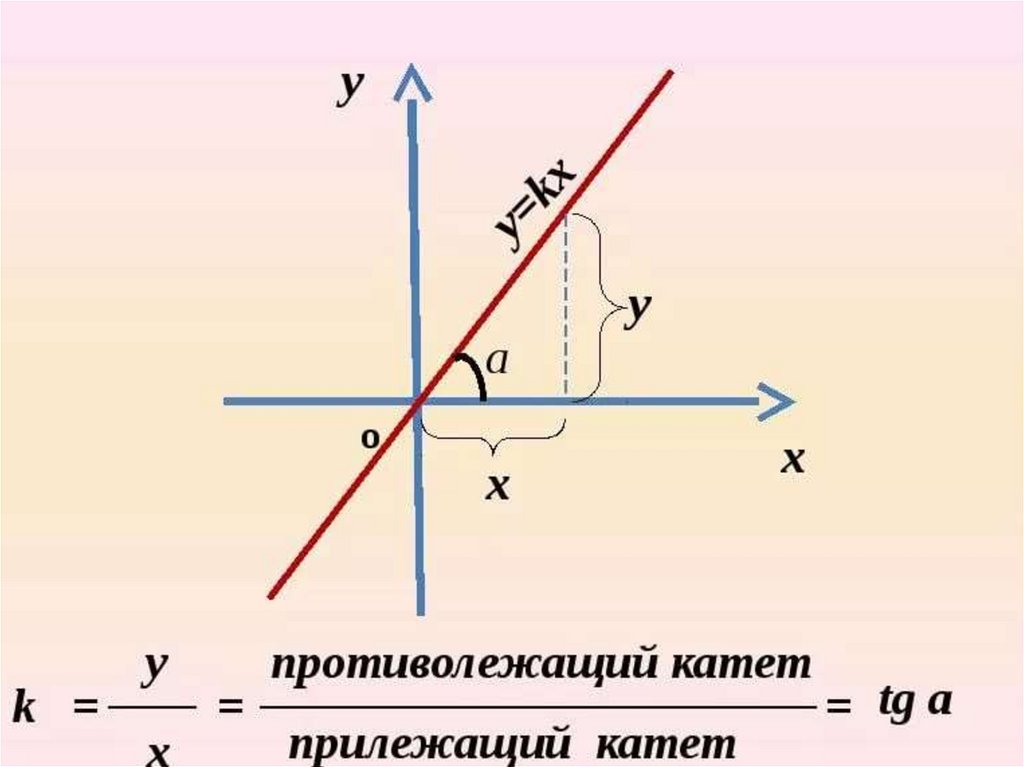
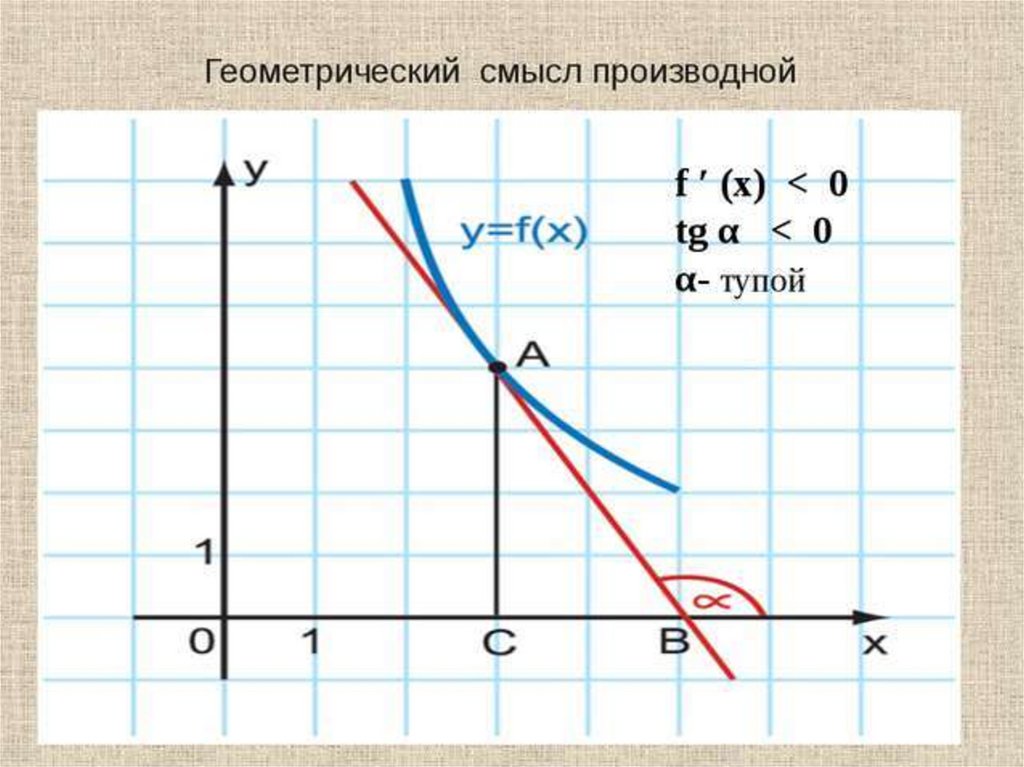
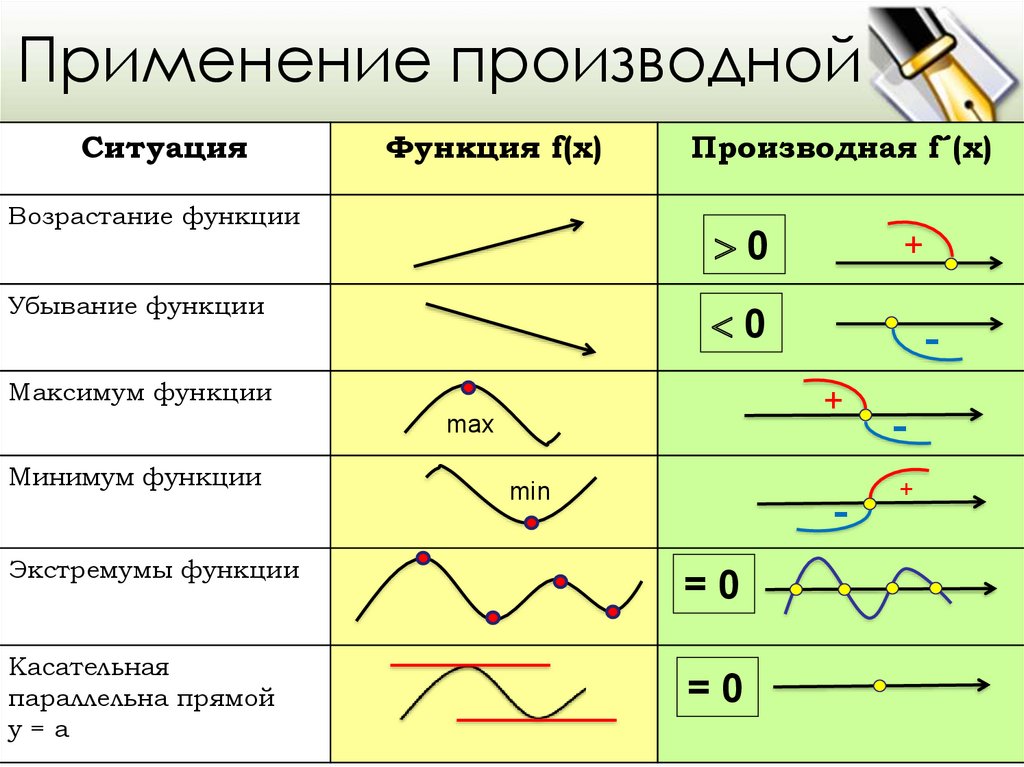
Применение производнойСитуация
Функция f(x)
Возрастание функции
Производная f´(x)
0
Убывание функции
0
Максимум функции
max
Минимум функции
Экстремумы функции
Касательная
параллельна прямой
у=а
+
min
=0
=0
+
-
-
+
14.
15.
16.
17.
18.
19.
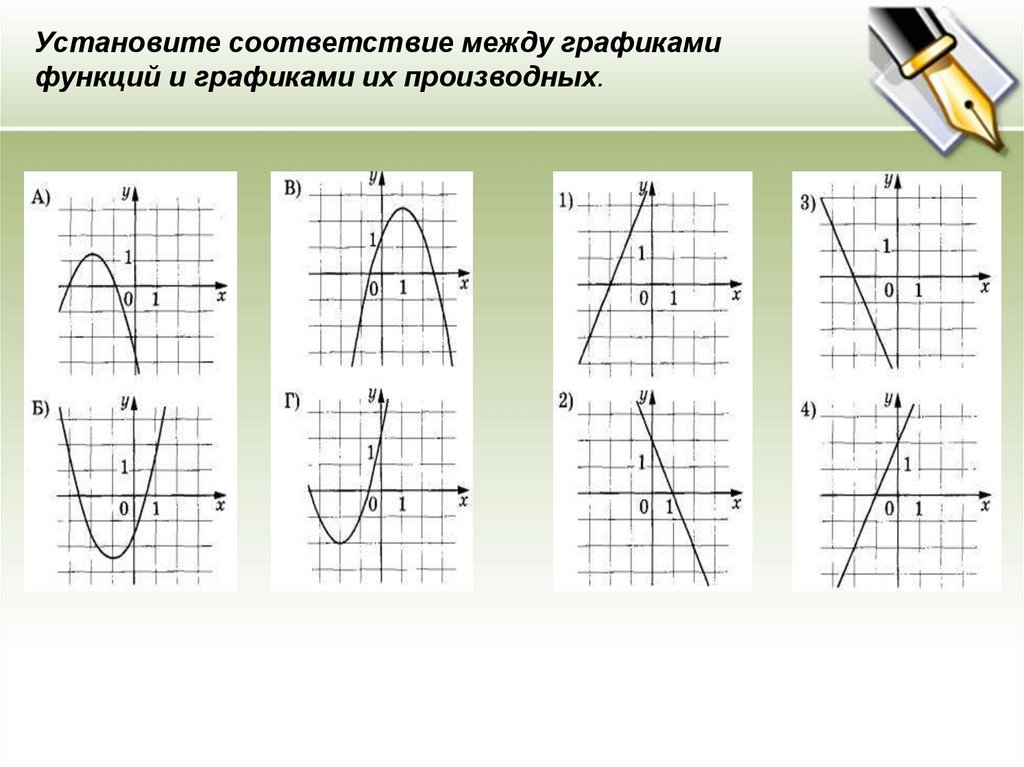
Установите соответствие между графикамифункций и графиками их производных.
20.
Ответ: 3421.21.
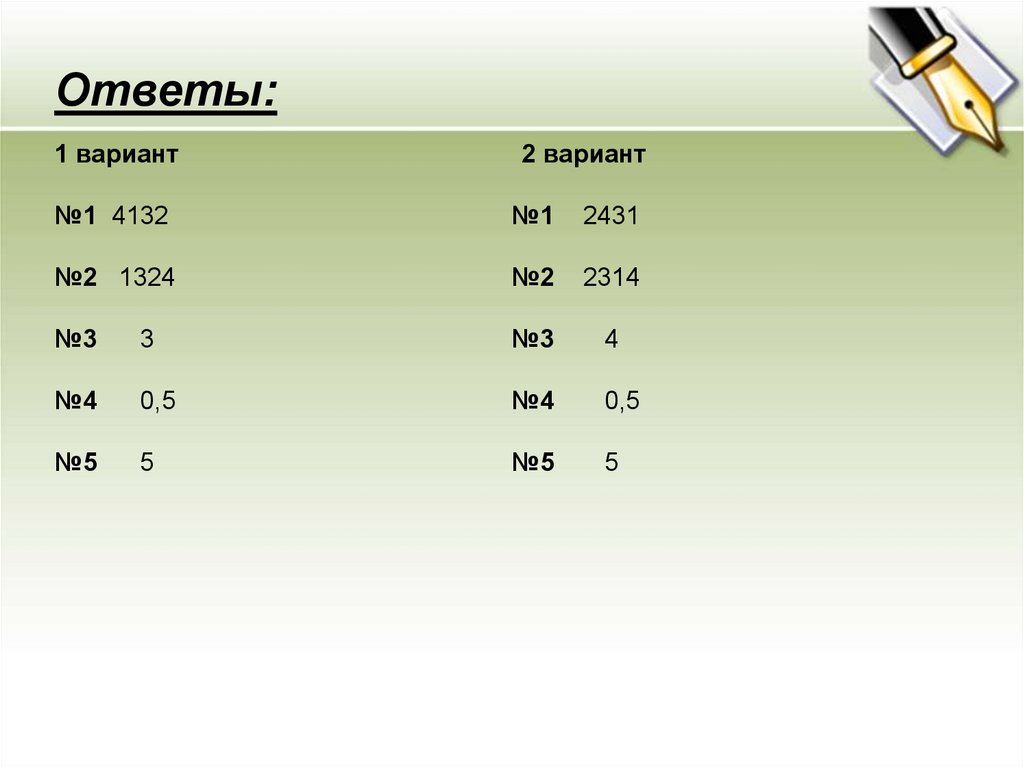
Ответы:1 вариант
2 вариант
№1 4132
№1
2431
№2 1324
№2
2314
№3
3
№3
4
№4
0,5
№4
0,5
№5
5
№5
5
22.
Д/зЗадание №14
из вариантов 1-10
23.
«Итоги»сегодня я узнал…
я понял, что…
я попробую…
я научился…
у меня не получилось …
• я смогу…
24.
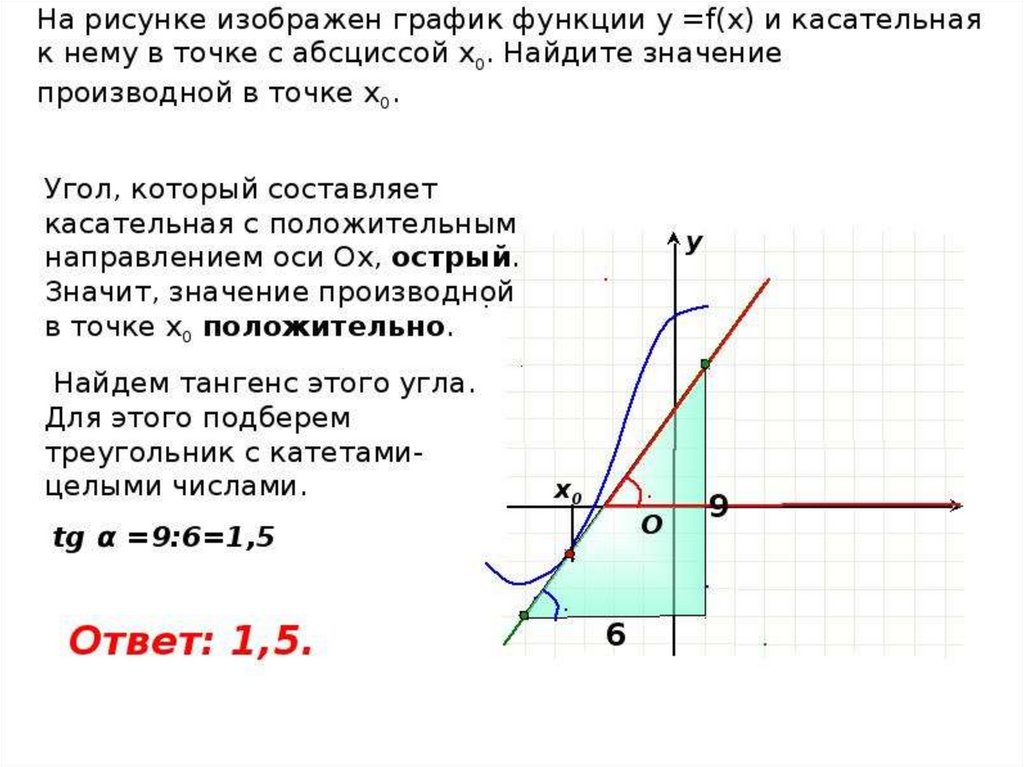
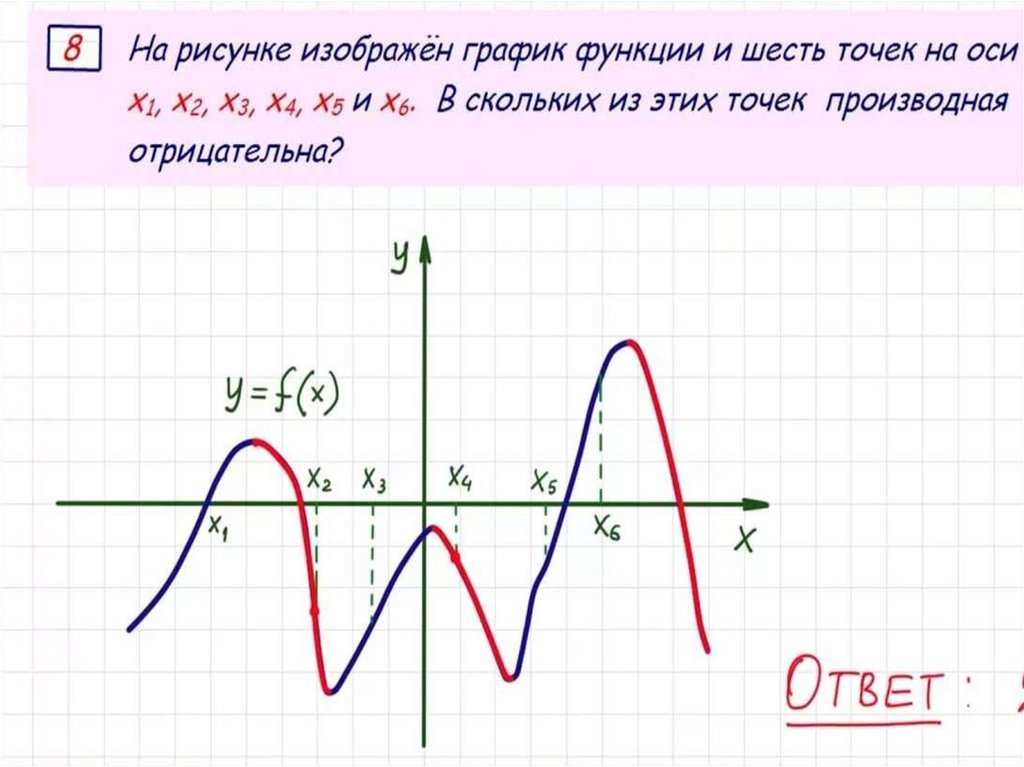
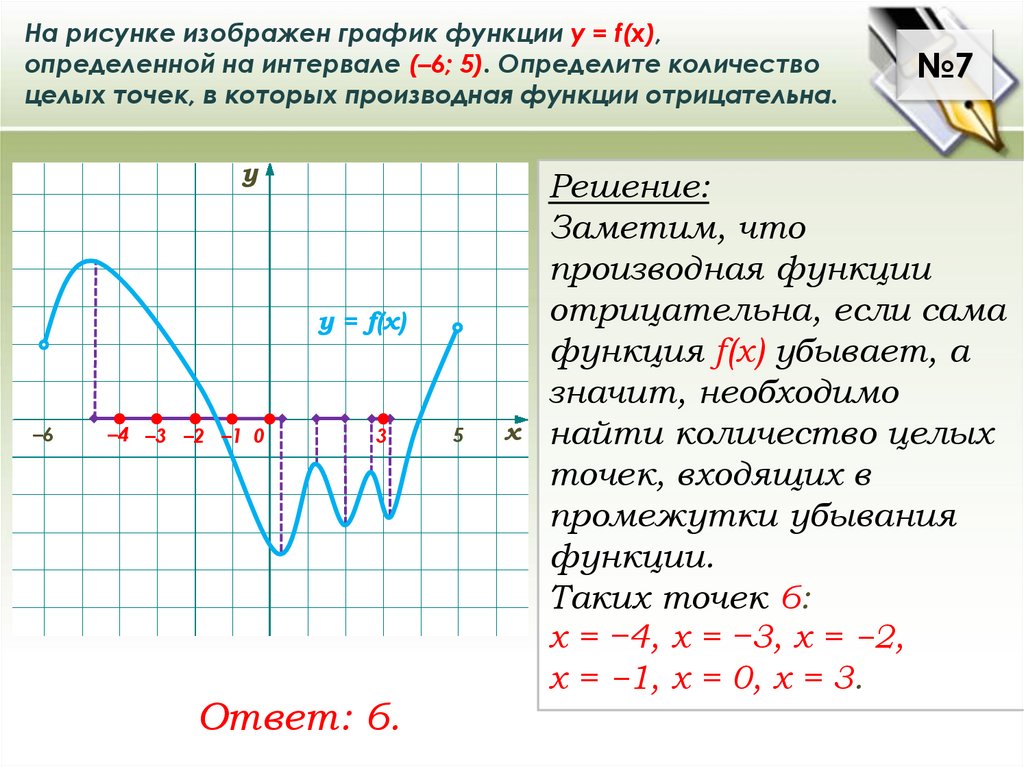
На рисунке изображен график функции у = f(x),определенной на интервале (–6; 5). Определите количество
целых точек, в которых производная функции отрицательна.
у
у = f(x)
–6
–4 –3 –2 –1 0
3
Ответ: 6.
5
х
№7
Решение:
Заметим, что
производная функции
отрицательна, если сама
функция f(x) убывает, а
значит, необходимо
найти количество целых
точек, входящих в
промежутки убывания
функции.
Таких точек 6:
х = −4, х = −3, х = −2,
х = −1, х = 0, х = 3.
25.
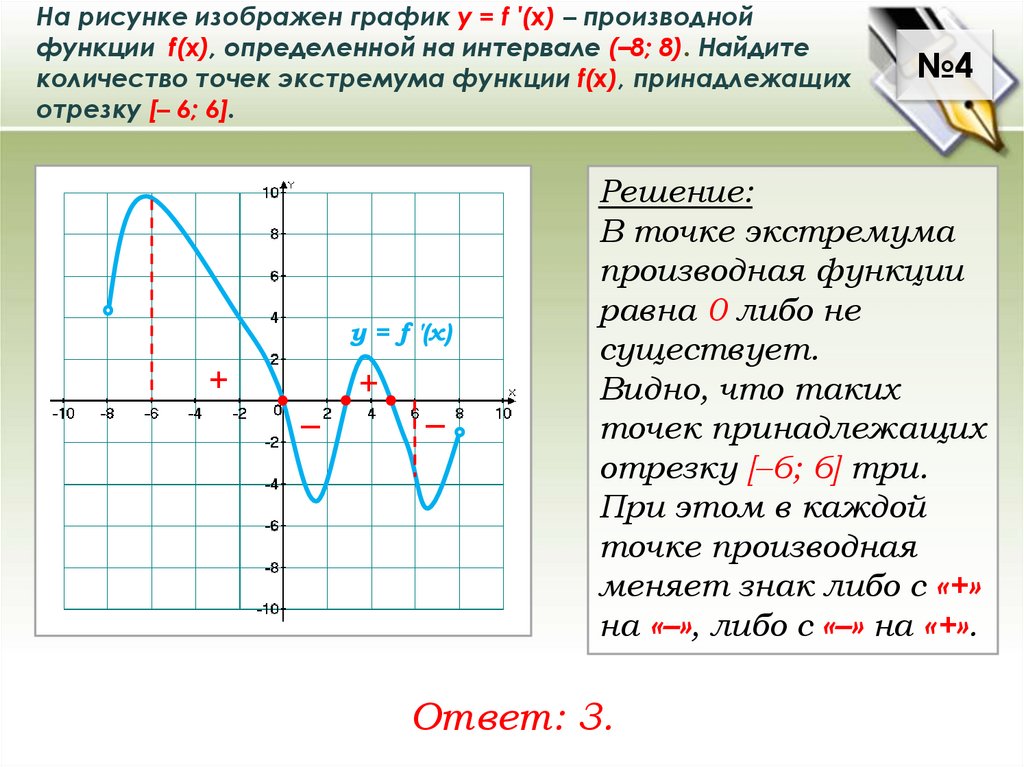
На рисунке изображен график у = f ′(x) – производнойфункции f(x), определенной на интервале (–8; 8). Найдите
количество точек экстремума функции f(x), принадлежащих
отрезку [– 6; 6].
у = f ′(x)
+
+
–
–
№4
Решение:
В точке экстремума
производная функции
равна 0 либо не
существует.
Видно, что таких
точек принадлежащих
отрезку [–6; 6] три.
При этом в каждой
точке производная
меняет знак либо с «+»
на «–», либо с «–» на «+».
Ответ: 3.
26.
«Знание – стольдрагоценная вещь,
что его не зазорно
добывать из любого
источника»
Ф. Аквинский
27.
Спасибоза
урок!








 mathematics
mathematics








