Свойство вписанных углов

1.

ДЗ п.88, 89 (4 теоремы,
доказательства 2 из
них - свойства)
Зачет по №№816 и 817
(по гот реш), №827829-833 (по рекоменд с
урока)

2.

Для успешного освоения одного из способов решения
задачи №827 следует повторить вопросы:
1) Свойство вписанных углов, опирающихся на одну дугу
2) Свойство вписанного угла, опирающегося на диаметр
3) Свойство острых углов прямоугольного треугольника
4) Мера центрального угла
5) Признаки равенства треугольников
6) Теорема Пифагора

3.

№827 - рекомендации
Докажите, что если диагонали вписанного четырёхугольника
перпендикулярны, то сумма квадратов противоположных
сторон четырёхугольника равна квадрату диаметра
описанной окружности
B
C Дано: АВСD – вписанный четырёхугольник;
3
4 2
K
•О
А
1
Е
АС ВD
и АС ∩ ВD = К;
Доказать: АВ ² + СD ² = ВЕ², где ВЕ – диаметр
описанной окружности
D Доказательство: (если нужно, используйте
1. Проведите хорду АЕ
рекомендации)
2. Сделайте заключение об углах 1 и 2.
3. Определите вид ΔВАЕ и ΔВКС.
4. Сделайте заключение об углах 3 и 4 и дугах АЕ и CD.
5. Докажите, что АЕ = СD ( доказав сначала, что ΔОАЕ = ΔСОD)
6. Примените теорему Пифагора для ΔВАЕ; используйте
равенство АЕ = СD для перехода к равенству АВ ² + СD ² = ВЕ²

4.

Для успешного освоения одного из способов решения
задачи №829 следует повторить вопросы:
1) Свойство вписанных углов, опирающихся на одну дугу
2) Признаки подобия треугольников
3) Основное свойство пропорции

5.

№829
Докажите, что в любом вписанном четырёхугольнике
произведение диагоналей равно сумме произведений
противоположных сторон (теорема Птолемея)
М
Дано: КМРЕ– вписанный четырёхугольник;
К
КР и МЕ его диагонали
Доказать: КР ∙ МЕ = КЕ ∙ МР + КМ ∙ РЕ
А
Р Доказательство: (рекомендации)
1. От луча МК отложите угол КМА, равный
углу РМЕ
2. Сделайте заключение об углах МКР и МЕР.
3. Учитывая шаги 1) и 2) сделайте заключение о ΔМКA и ΔМЕР.
4. Запишите пропорцию и примените основное её свойство
5. Найдите ещё пару подобных треугольников
6. Запишите пропорцию и примените основное её свойство
7. Сложите равенства из пунктов 4 и 6, сравните с тем, что
надо было доказать
Е

6.

Для успешного освоения одного из способов решения
задачи №833 следует повторить вопросы:
1) Свойство отрезков касательных, проведённых из одной точки
2) (а
+ b + c) ² = а² + b² + c² + 2аb + 2bc + 2аc
3) Теорема Пифагора
4) Чему равна площадь трапеции (через основания и высоту)

7.

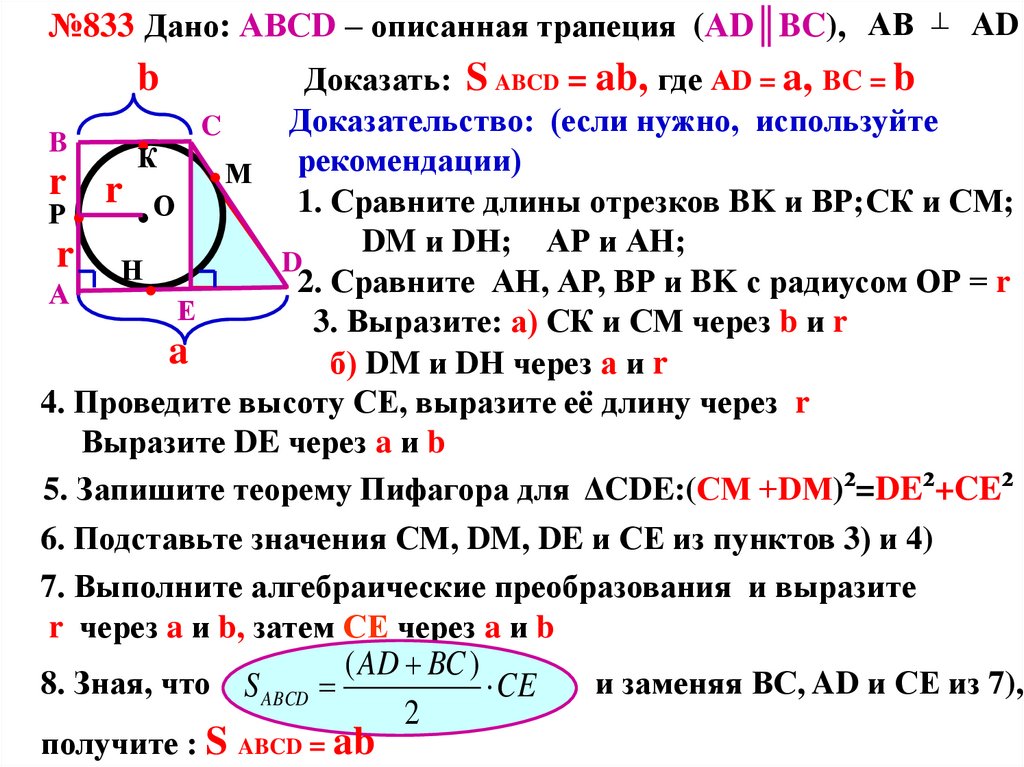
№833 Дано: АВСD – описанная трапеция (АD║BC), АВ
АD
Доказать: S ABCD = ab, где АD = a, BC = b
Доказательство: (если нужно, используйте
C
B
•К
рекомендации)
М
r r
1. Сравните длины отрезков BK и ВР; СК и СМ;
Р
•О
DM и DН; АР и АН;
r Н
D
2. Сравните АН, АР, ВР и BK с радиусом ОР = r
А
Е
3. Выразите: а) СК и СМ через b и r
a
б) DM и DН через а и r
4. Проведите высоту СЕ, выразите её длину через r
Выразите DE через a и b
5. Запишите теорему Пифагора для ΔCDE:(СМ +DМ)²=DE²+CE²
b
6. Подставьте значения СМ, DM, DE и СЕ из пунктов 3) и 4)
7. Выполните алгебраические преобразования и выразите
r через a и b, затем СЕ через a и b
8. Зная, что
получите : S
( AD BC )
S ABCD
CE
2
ABCD
= ab
и заменяя ВС, AD и СЕ из 7),