Системы счисления. Двоичная система счисления

1.

СИСТЕМЫ СЧИСЛЕНИЯ.
Двоичная система
счисления
8 класс

2.

Система счисления - это правила записи чисел
определенным для системы алфавитом.
Алфавит системы счисления - совокупность
цифр.
Цифры - знаки, при помощи которых
записываются числа.

3.

Унарная система счисления
непозиционная система счисления с единственной цифрой,
обозначающей 1.
Для записи любых чисел можно было
использовать один символ - палочка,
узелок, зарубка, камушек.

4.

ВАВИЛОНСКАЯ СИСТЕМА
СЧИСЛЕНИЯ
40 веков до нашего времени создалась
позиционная нумерация, то есть такой способ
записи чисел, при котором одна и та же цифра
может обозначать разные числа, смотря по
месту, занимаемому этой цифрой. В
вавилонской поместной нумерации ту роль,
которую у нас играет число 10, играет число
60, и потому эту нумерацию называют
шестидесятеричной
Китайская нумерация
Эта нумерация одна из старейших и самых
прогрессивных, поскольку в нее заложены такие
же принципы, как и в современную арабскую,
которой мы с Вами пользуемся. Возникла эта
нумерация около 4 000 тысяч лет тому назад в
Китае.

5.

Славянская кириллическая нумерация
Эта нумерация была создана греческими монахами братьями Кириллом
(Константином) и Мефодием в IX веке.
Эта форма записи чисел имела
полное сходство с греческой
записью чисел.
Если посмотреть внимательно, то
увидим, что после "а" идет буква
"в", а не "б" как следует по
славянскому алфавиту, то есть
используются только буквы,
которые есть в греческом
алфавите. До XVII века эта форма
записи чисел была официальной
на территории современной
России, Белоруссии, Украины,
Болгарии, Венгрии, Сербии и
Хорватии. До сих пор
православные церковные книги
используют эту нумерацию.

6.

Системы счисления
В непозиционных
системах счисления
– количественное
значение цифры не
зависит от ее
позиции в числе
Единицы Десятки Сотни Тысячи
1
10
100
1000
2
20
200
2000
3
30
300
3000
4
40
400
5
50
500
6
60
600
7
70
700
8
80
800
9
90
900

7.

В основе Римской системы счисления лежат знаки I (один
палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две
сложенные ладони) для 10.
Для обозначения чисел
специальные знаки
В римских числах цифры записываются слева направо в порядке убывания. Числа
получаются с учётом следующего правила: Величина числа определяется как сумма
или разность чисел. Если меньшая цифра стоит слева от большей, то она вычитается,
если справа- прибавляется.
девять записывается как IX, т. е. десять минус один,
семь — VII (пять плюс два),
Сорок пять—XLV (пятьдесят минус десять плюс пять),
восемьдесят четыре—XXCIV (сто минус двадцать плюс пять минус один).

8.

В позиционных СС количественное
значение цифры зависит от ее позиции в
числе
Алфавит десятичной системы составляют цифры
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Число 548
5 обозначает пять сотен,
4 – четыре десятка,
8 –восемь единиц.
Если поменять местами цифры, например, 5 и 4, то
цифра 5 – станет обозначать пять десятков, 4 – четыре
сотни.

9.

Основная формула развернутой записи
числа
В позиционной системе счисления с основанием
q любое число может быть представлено в виде:

10.

Часто используемые
позиционные системы счисления
Система счисления
Алфавит системы
Десятичная
012345789
Основание
системы
n=10
Двоичная
0, 1
n=2
Восьмеричная
01234567
n=8
Шестнадцатеричная 0...9, А(10), B(11), C(12), n=16
D(13), E(14), F(15)

11.

Правило перевода целых десятичных чисел в
систему счисления с основанием q
1.последовательно выполнять деление
числа на основание нужной системы счисления
до тех пор, пока не получим частное, равное нулю;
2.полученные остатки, являющиеся цифрами числа
в новой системе счисления, привести в
соответствие с алфавитом новой системы
счисления
3.составить число в новой системе счисления,
записывая его, начиная с последнего полученного
остатка.

12.

Вся информация в компьютере цифровых устройствах
представлена в виде двоичного кода. Компьютер
переводит информацию в последовательность нулей и
единиц.
Двоичной системой счисления называется
позиционная система счисления с основанием 2.
Двоичный алфавит: 0 и 1.

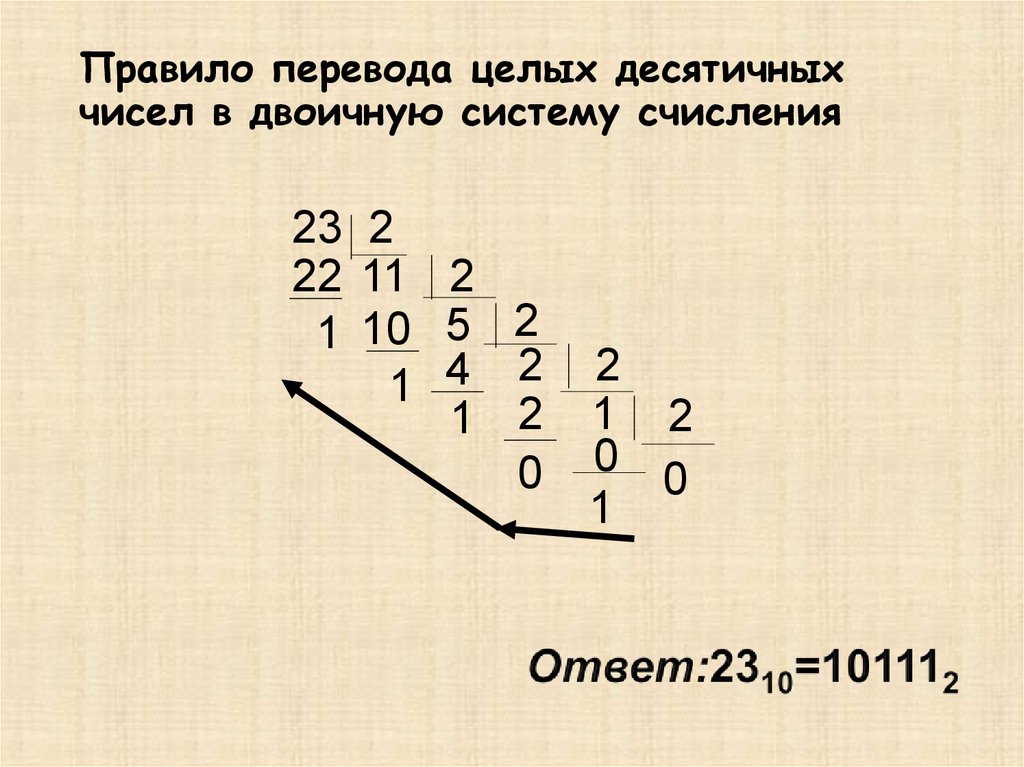
13.

Правило перевода целых десятичных
чисел в двоичную систему счисления
23 2
22 11 2
1 10 5 2
2
4
1
1 2
0
2
1 2
0
0
1

14.

Способ перевода в двоичную систему
счисления с помощью таблицы числа 2n
2510= 1610+810+1=24+23+1=
100002+10002+12=110012

15.

Правило перевода из
двоичной систему счисления
в десятичную
110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 2710
Или такой вариант

16.

Закрепление изученного материала
4810 = ?2
10101012 = ?10

17.

Домашнее задание
Учебник:
с. 14 № 6 ; № 7 (а);
с. 15 № 13