Двоичная системя счисления

1.

Кодирование информации
Для хранения, передачи и обработки информации в ЭВМ ее
надо представить в виде цифровых кодов.
Эта операция называется кодированием информации.
Для кодирования информации в ЭВМ используется двоичная
система счисления.

2.

Позиционные и непозиционные системы счисления
Система счисления – это совокупность символов,
используемых для изображения чисел.
Система счисления включает в себя:
•алфавит, т. е. набор символов для записи чисел,
•способ записи чисел

3.

Системы счисления делятся на два класса:
•позиционные
•Непозиционные
В позиционной системе значение или вес цифры в записи
числа зависит от ее положения (позиции) в числе.
В непозиционной системе или вес цифры в записи числа
не зависит от ее положения (позиции) в числе.
Непозиционной системой счисления является римская
система.

4.

Рассмотрим вопрос в общем.
Пусть основание позиционной системе счисления равно S, а
алфавит состоит из S символов – ε1 , ε2 , ε3 ,… εS.
Любое число X в позиционной системе счисления можно
представить в виде полинома от степеней основания S:
r
r
1
10
1
2
X
S
S
...
S
S
S
S
...
r
r
1
1
0
1
2
Здесь коэффициентами разложения εi являются любые из S
символов ε1 , ε2 , ε3 ,… εS.
Для краткости число X изображают в виде последовательности
коэффициентов разложения εi:
X
...
.
...
r
r
1
1
0
1
2

5.

Позиционной является привычная для нас в повседневной
жизни десятичная система счисления, в которой значение (вес)
цифры зависит от ее позиции в записи числа.
В числе 1111 одна и та же цифра 1 означает последовательно
единицу, десяток, сотню, тысячу
В десятичной системе счисления основание равно 10,
Алфавит состоит из 10 символов, цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

6.

В 2-ной системе основание равно 2, алфавит состоит из 2
цифр - 0 и 1.
В 16-ной системе основание равно 16, алфавит состоит из16
символов:
•10 десятичных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
•6 символов латинского алфавита, которым присвоены
соответствующие десятичные значения:
A=10,
B=11,
C=12,
D=13,
E=14,
F=15

7.

16-ая
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10-ая
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2-ая
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

8.

Позиции цифры, отсчитанные от запятой (точки),
отделяющей целую часть от дробной, называются
разрядами.
В позиционной системе счисления вес каждого разряда
больше соседнего в S число раз.

9.

Число в двоичной и шестнадцатеричной системах
счисления обычно обозначают с помощью подстрочного
символа, соответствующего основанию счисления:
Например:
11012
BF16

10.

Пример.
В десятичной системы счисления некоторое число вид
X=6321.564= 6321.56410.
Значение X можно записать в виде:
X 6 103 3 10 2 2 101 1 100 5 10 1 6 10 2 4 10 2
Веса разряда и коэффициенты εi для этого числа
будут следующими:
Веса 103 102 101 100 10-1
r
6
3
2
1
5
10-2
10-3
6
4

11.

Двоичная система счисления
В двоичной системе счисления основание S = 2, т.е.
используются всего два символа: 0 и 1.
Достоинства двоичной системы:
•для представления в машине разряда двоичного числа
может быть использован любой простой элемент, имеющий
всего два устойчивых состояния;
•простота двоичной арифметики.
Сложение
0+0=0
Вычитание
0-0=0
Умножение
0*0=0
0+1=1
1-0=1
1*0=0
1+0=1
1-1=0
0*1=0
1+1=10
10-1=1
1*1=1

12.

Двоичная система счисления проще десятичной.
Однако двоичное изображение числа требует большего
числа разрядов.

13.

В общем виде двоичное число выглядит следующим
образом:
r
r
1
1
0
1
2
X
2
2
...
2
2
2
2
...
r r
1
1
0
1
2
где εi =0,1.
Вес каждого разряда в двоичной системе счисления
кратен 2 или 1/2.
Пример.
Двоичное число: A=1011101.0112.
A 1 2 6 0 25 1 2 4 1 23 1 2 2 0 21 1 2 0 0 2 1 1 2 2 1 2 3
Веса 26=64 25=32 24=16 23=8 22=4 21=2 20=1 2-1=0.5 2-2=0.25
1
0
1
1
1
0
1
0
1
2-3=0.125
1

14.

Преобразование двоичных чисел в десятичные
Для преобразования двоичных чисел в десятичные
необходимо сложить десятичные веса всех разрядов
двоичного числа, в которых содержатся единицы.
A=1011101.0112.
A 1 26 0 25 1 2 4 1 23 1 2 2 0 21 1 2 0 0 2 1 1 2 2 1 2 3
A 1 64 0 32 1 16 1 8 1 4 0 2 1 1 0 0.5 1 0.25 1 0.125 93.375

15.

Преобразование десятичных чисел в двоичные
Перевод чисел из десятичной системы счисления в двоичную систему
счисления производится следующим образом:
•перевод целой части:
десятичное число последовательно делят на 2, выделяя остатки.
Процедуру повторяют до тех пор пока частное, полученное в результате
очередного деления, не будет равно 0.
Остатки, записанные в обратном порядке, образуют число в двоичной
системе исчисления.
•перевод дробной части:
дробную часть десятичного числа последовательно умножают на 2,
выделяя целые части. Эту процедуру повторяют до тех пор, пока
результат умножения не будет точно равен 1, либо не будет достигнута
требуемая точность.
Целые части , записанные в прямом порядке, образуют дробную часть
числа в двоичной системе исчисления.

16.

Пример перевода из десятичной в двоичную: 999,35
Целая часть -999:
999=11111001112
Проверка:
11111001112 29 28 27 26 25 2 2 21 20
512 256 128 64 32 4 2 1 999
Вывод: Значения чисел совпадают, перевод произведен правильно.

17.

Дробная часть: 0,35
0,35=0,01011002
-2
4
5
Проверка: 0,35 0,0101100 2 2 2 0,25 0,0625 0,03125 0,34375
Итак: 999.3510=1111100111,01011002

18.

Примеры:
548=
10 0010 01002
238=
1110 11102
6139=
1 0111 1111 10112
0.5893 0.1001 0110 1101 1100 01012
0.0175 0.0000 0100 0111 1010 11102
0.3046875=
0.0100 11102

19.

Для перевода целого число из двоичной системы в
шестнадцатеричную, его нужно разбить на тетрады, начиная с
младшего разряда, в случае необходимости дополнив старшую
тетраду нулями, и каждую тетраду заменить соответствующей
шестнадцатеричной цифрой.
Пример. Число 10111000112 перевести в шестнадцатеричную
систему счисления.
10111000112 = 0010 1110 00112 =2E32
Для перевода шестнадцатеричного числа в двоичное необходимо
каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число перевести в двоичную систему счисления.
EE816=1101 1101 10002

20.

Двоичная арифметика
Правила выполнения арифметических действий над
двоичными числами определяются арифметическими
действиями над одноразрядными двоичными числами.
Сложение
0+0=0
Вычитание
0-0=0
Умножение
0*0=0
0+1=1
1-0=1
1*0=0
1+0=1
1-1=0
0*1=0
1+1=10
(перенос в старший разряд)
10-1=1
1*1=1

21.

Правила выполнения арифметических действий во всех
позиционных системах счисления аналогичны.
Сложение
Пример.
Сложить два числа в десятичном и двоичном
представлении.
9910 и 9510 .
Сложение в десятичном представлении:
переносы
1 слагаемое
2 слагаемое
сумма
1
1
1
9
9
9
9
5
4

22.

Переводим из десятичной в двоичную:
Слагаемое 1
09910 =011000112
Слагаемое 2
09510 =010111112
Сложение в двоичном представлении:
переносы
1 1 1 1
1 слагаемое
1 1 0
2 слагаемое
1 0 1
сумма
1 1 0 0
1
0
1
0
1
0
1
0
1
1 1
1 1
1 0
Проверка результата:
Переводим: 110000102= 19410
99+94=194
Вывод: Результаты сложения в десятичной и двоичной
системе одинаковы, результат сложения верен.

23.

Вычитание
Пример.
Вычесть из числа 10910 число 04910 в десятичном и
двоичном представлении:
Вычитаем в десятичном представлении:
заем
1
1 слагаемое 1 0 9
2 слагаемое
4 9
сумма
6 0

24.

Переводим в двоичную систему:
Уменьшаемое
Вычитаемое
10910 =
04910 =
011011012
001100012
Вычитаем в двоичной системе:
заем
Уменьшаемое
Вычитаемое
Разность
1
1 1
1
1
1
0 1 1 0 1
1 0 0 0 1
1 1 1 0 0
Проверка результата:
Переводим: 1111002=
6010
109-49=60
Вывод: Результаты вычитания в десятичной и двоичной
системе одинаковы, результат вычитания верен.

25.

Умножение
Операция перемножения многоразрядных чисел производится
путем образования частичных произведений и
последующего их суммирования.
Частичные произведения формируются в результате
умножения множимого на каждый разряд множителя.
Каждое частичное произведение смещено относительно
предыдущего на один разряд.

26.

Переводим в двоичную форму:
2910=111012
1310=11012
Вычисляем произведение в двоичной форме (в «ручном» виде):
1 множитель
2 множитель
1 частичное произведение
2 частичное произведение
3 частичное произведение
4 частичное произведение
Произведение
0
1 1
1 1 1 1
1 0 1 1
1 1
1
1 1
0 0
1 0
0 1
1 1
1
1
1
0
1
0 1
0 1
0 1
0
0 0 1
Проверка результата:
Переводим: 1011110012= 37710
29*13=377
Вывод: Результаты умножения в десятичной и двоичной
системе одинаковы, результат умножения верен.

27.

Умножение в ЭВМ («Машинное» умножение)
В ЭВМ процесс суммирования частичных произведений
производится последовательно:
формируется одно частичное произведение,
• к нему с соответствующим сдвигом прибавляют
следующее частичное произведение
• и т.д.
Т.е. не формируются не все частичные произведения сразу.

28.

Поскольку умножение идет в двоичной системе
счисления, то частичное произведение:
•равно либо 0 (если в соответствующем разряде
множителя стоит 0),
•либо является копией множимого, смещенного на
соответствующее число разрядов влево (если в разряде
множителя стоит 1).

29.

Рассмотрим на примере два машинных варианта
выполнения умножения целых чисел:
•начиная со старшего частичного произведения
(“старшими разрядами вперед”)
•начиная с младшего частичного произведения
(“младшими разрядами вперед”).

30.

Метод умножения «старшими разрядами вперед»
1. Формируется первое частичное произведение: первый
множитель умножается на старший разряд второго
множителя,
2. Результат сдвигается на один разряд влево
3. Формируется второе частичное произведение: первый
множитель умножается на второй по старшинству
разряд второго множителя
4. Складываются первое частичное произведение
(смещенное) со вторым частичным произведением
5. И т.д., повторяются пункты 2, 3 и 4.

31.

Найти произведение двух чисел
X*Y=29*13=111012*11012= 373.
Умножение старшими разрядами вперед:
1 множитель
2 множитель
Умножение на 1101
Сдвиг влево
Умножение на 1101
Сложение
Сдвиг влево
Умножение на 1101
Сложение
Сдвиг влево
Умножение на 1101
Произведение
1
1 0
1 0 1
1 0 1
1 0 1 0
1 0 1 1
1 1
1
1 1
1 1
1 1
1 0
0 1
0 0
0 1
1 1
1 1
1 1
1
1
1
0
1
1
1
0
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
1
0
1
1
0
0
0
0
1
1
Проверка: 1011110012=373
29*13=373
Вывод: Результаты умножения в десятичной и двоичной
системе одинаковы, результат умножения верен.

32.

Метод умножения «младшими разрядами вперед»
1. Формируется первое частичное произведение: первый
множитель умножается на младший разряд второго
множителя,
2. Результат сдвигается на один разряд вправо
3. Формируется второе частичное произведение: первый
множитель умножается на второй младший разряд
второго множителя
4. Складываются первое частичное произведение
(смещенное) со вторым частичным произведением
5. И т.д., повторяются пункты 2, 3 и 4.

33.

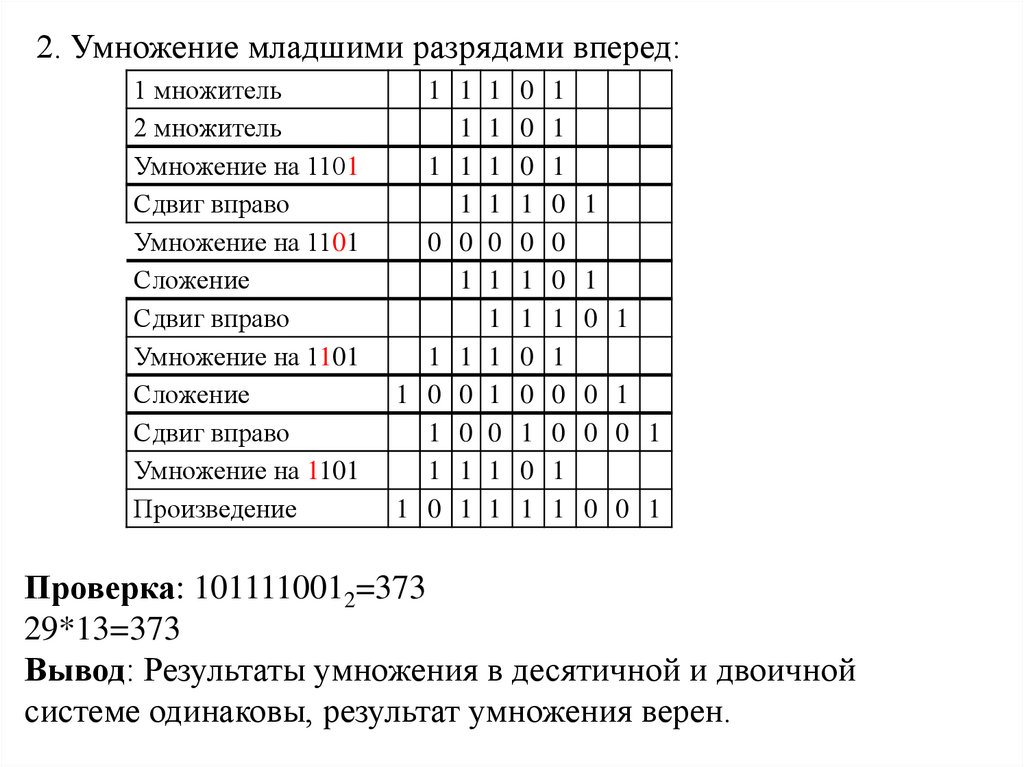
2. Умножение младшими разрядами вперед:
1 множитель
2 множитель
Умножение на 1101
Сдвиг вправо
Умножение на 1101
Сложение
Сдвиг вправо
Умножение на 1101
Сложение
Сдвиг вправо
Умножение на 1101
Произведение
1 1
1
1 1
1
0 0
1
1
1 0
1
1
1 0
1
0
0
1
1
1
1
1
1
0
1
1
1
1
0
1
1
0
0
0
1
0
1
1
0
0
1
0
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0 1
0 1
0 0 1
0 0 1
Проверка: 1011110012=373
29*13=373
Вывод: Результаты умножения в десятичной и двоичной
системе одинаковы, результат умножения верен.

34.

Деление
Деление – операция, обратная умножению, поэтому при
делении двоичных чисел, так же как и в десятичной
системе счисления, операция вычитания повторяется до тех
пор, пока уменьшаемое не станет меньше вычитаемого.
Число этих повторений показывает, сколько раз вычитаемое
укладывается в уменьшаемом.
Пример.
Вычислить 204 /12 в двоичном коде.
204=110011002;
12=11002

35.

Пример (самостоятельно)
Найти частное 2223/57 в двоичном представлении.