Similar presentations:
Анализ нелинейных резистивных электрических цепей. Корректирующие цепи
1. Лекция 6
Анализ нелинейныхрезистивных
электрических цепей.
Корректирующие цепи
1
2. Нелинейные элементы
В ряде случаев можно говорить о• нелинейном сопротивлении R(i)
или R(u),
• нелинейной индуктивности L(i)
или L(u) и
• нелинейной ёмкости C(i) или С(u)
2
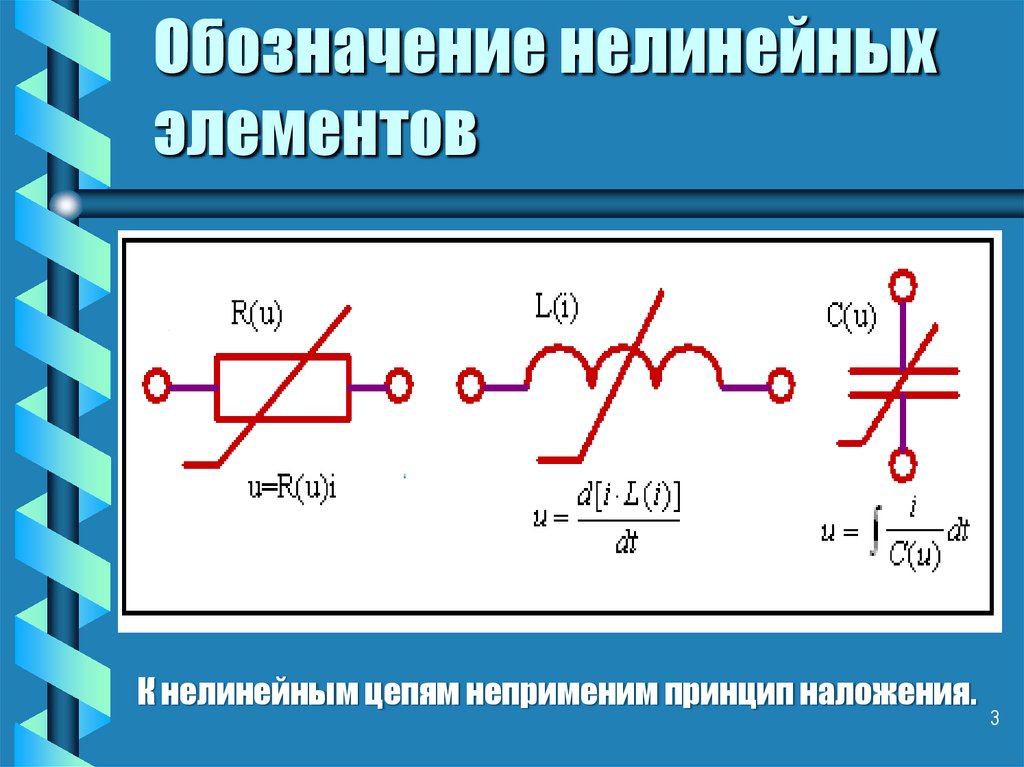
3. Обозначение нелинейных элементов
К нелинейным цепям неприменим принцип наложения.3
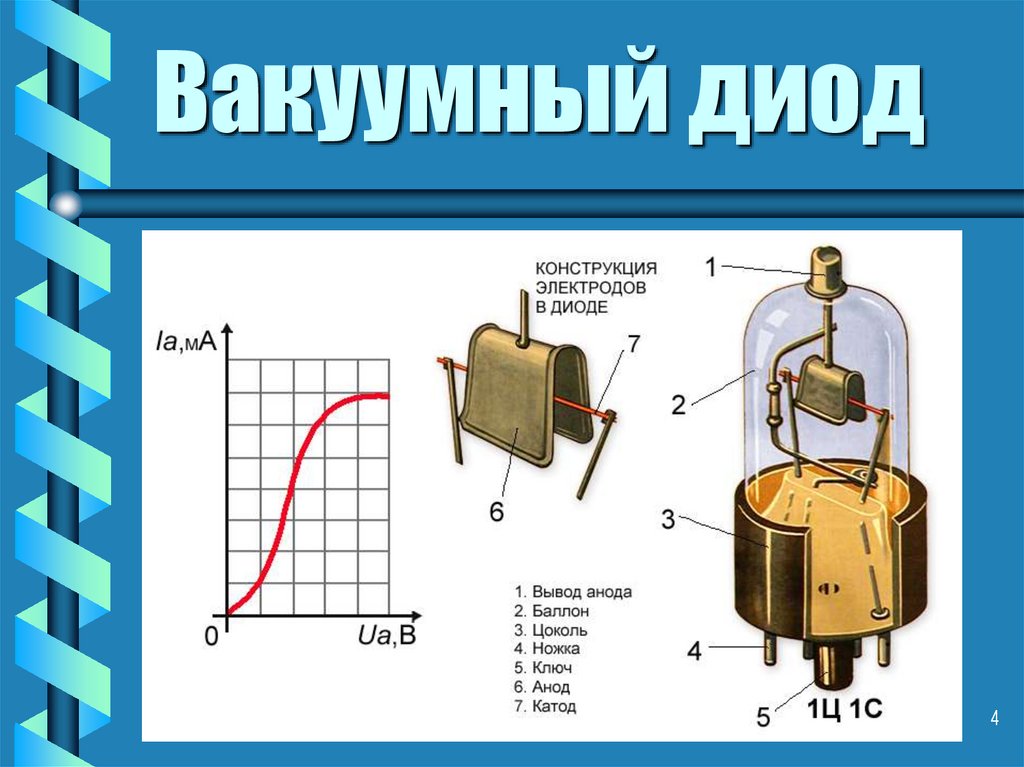
4. Вакуумный диод
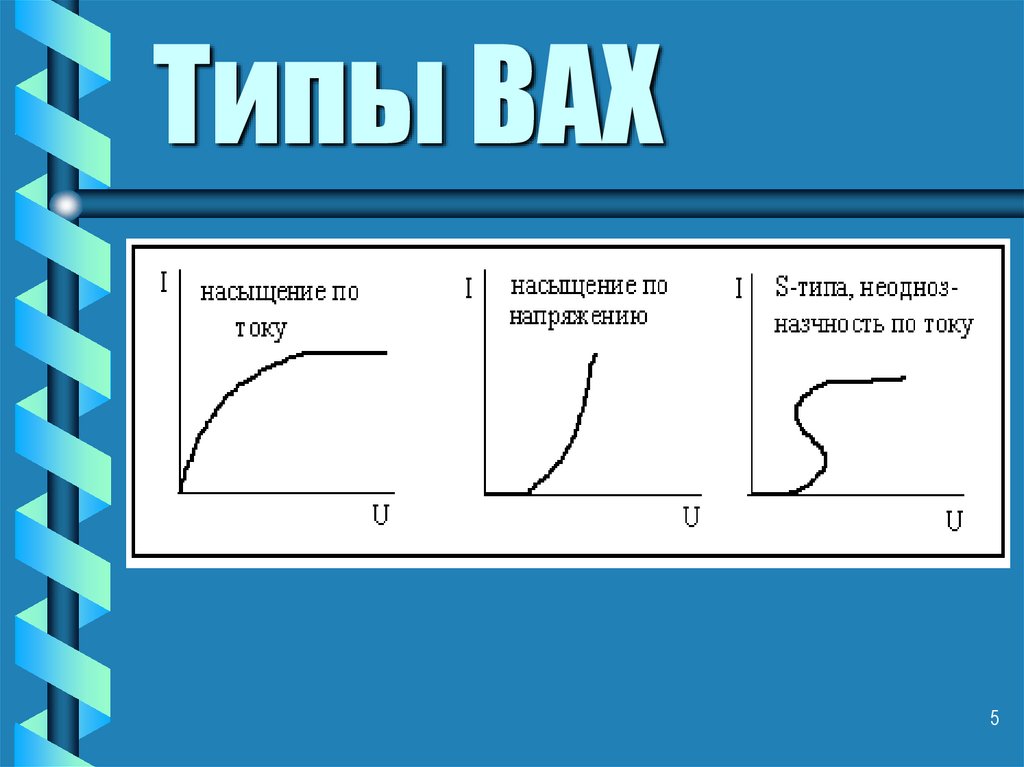
45. Типы ВАХ
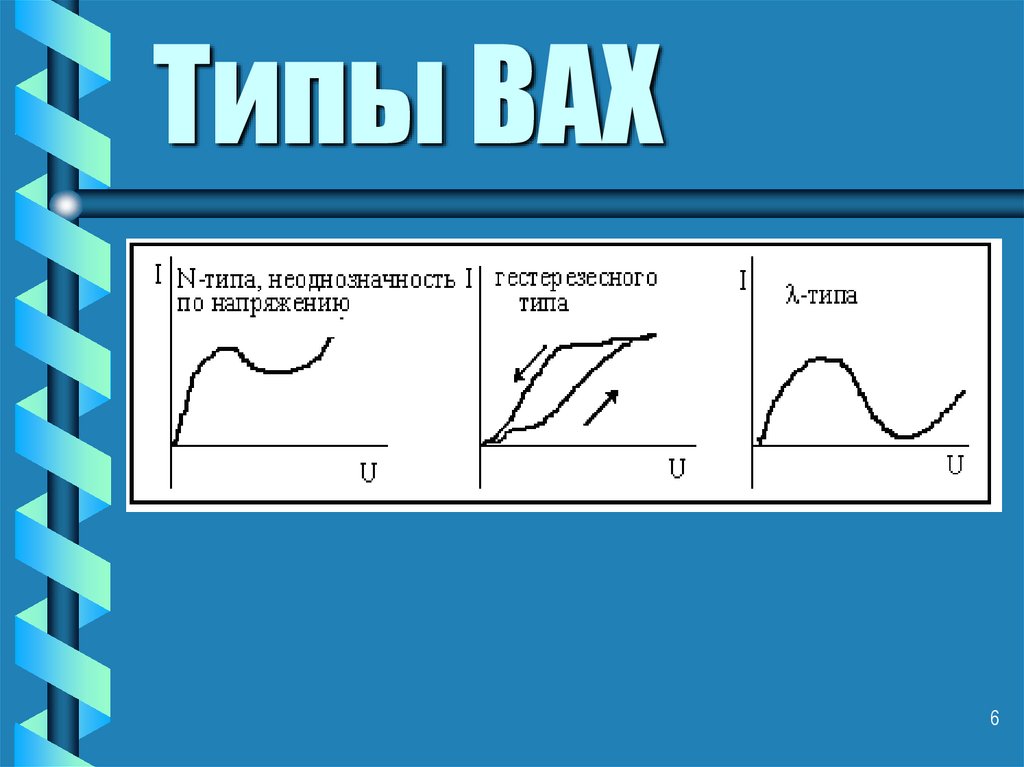
56. Типы ВАХ
67. Анализ электрической цепи с одним нелинейным двухполюсником в режиме постоянного тока
Расчет по постоянному току заключается вотыскании рабочей точки и обычно
является первым шагом при анализе
нелинейных цепей.
• Затем требуется решение нелинейных
алгебраических уравнений.
• Следует иметь ввиду, что после решения
этих уравнений необходимо обязательно
проверить получившееся решение на их
физическую реализуемость.
7
8. Нахождение рабочей точки
Существуют графические методы
нахождения рабочей точки, которые
удобны и наглядны для анализа простых
схем, но малопригодны для расчета
сложных схем, поскольку графические
методы не обладают достаточной
точностью, не дают возможности
устанавливать общие закономерности,
определять оптимальные решения,
варьировать параметрами цепи и т.д.
8
9. В настоящее время
наиболее предпочтительнымиявляются аналитические методы
расчета с помощью ЭВМ,
основывающиеся на
аппроксимации ВАХ или замене
нелинейной характеристики
аналитической функцией,
приближенно выражающей
заданную зависимость.
9
10. Пример
• Определить ток в цепи ,состоящей из двух
последовательно соединенных
линейного двухполюсника с
резистивным сопротивлением
R=10 Ом и нелинейного
двухполюсника с ВАХ: I 0, U 0,
U=aI+bI2 , где a=6 В/А, b=2 В/А2 ,
Е=18 В.
10
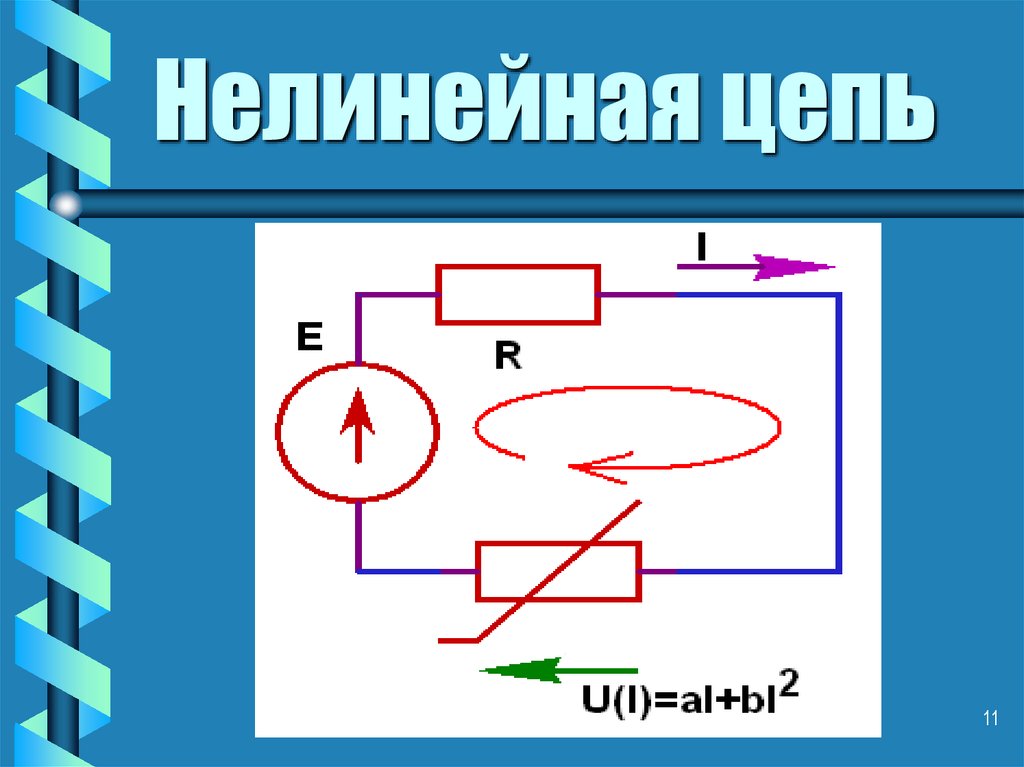
11. Нелинейная цепь
1112. Решение
• Запишем уравнения по2 закону Кирхгофа
• RI+U(I)=E
12
13. Ответ
после подстановки зависимости U(I) получим
2
• RI+aI+bI =E,
• bI2+(R+a)I-E=0
• 2I2+16 I-18=0
• I1=1 A, I2=-9 A.
• Выбираем I=1 A, поскольку I=-9 A не удовлетворяет
условиям аппроксимации и следовательно не имеет
физического смысла.
13
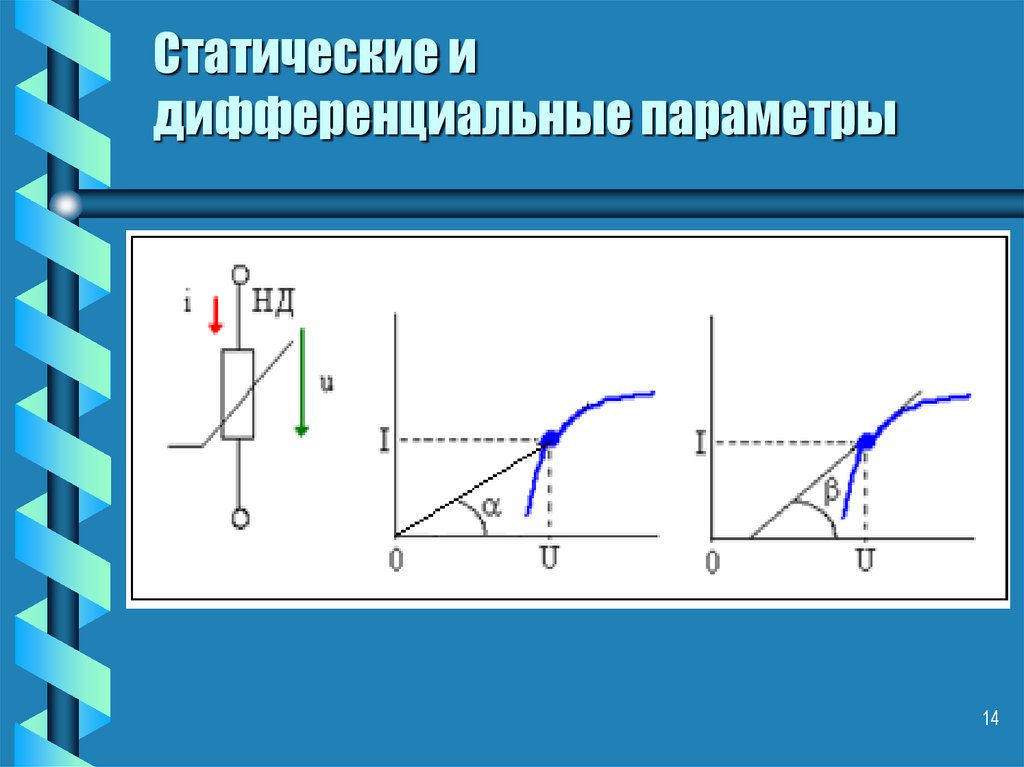
14. Статические и дифференциальные параметры
1415. Статическое сопротивление
При постоянном напряжении u=U в цепибудет протекать ток I=f(U). Отношение U/I
называется статическим сопротивлением
или сопротивлением данного элемента
постоянному току, т.е.
• RСТ =U/I,
• где I – ток, текущий в цепи при
напряжении U на зажимах нелинейного
двухполюсника.
15
16. Дифференциальное сопротивление
1617. Дифференциальное сопротивление
нелинейного двухполюсникаможно рассматривать как
сопротивление этого
элемента для малых
приращений, т.е. как
сопротивлению переменному
току.
17
18. В общем случае
R R .СТ d
•Эти понятия совпадают только для
линейных двухполюсников в которых
R
= R = R.
СТ d
18
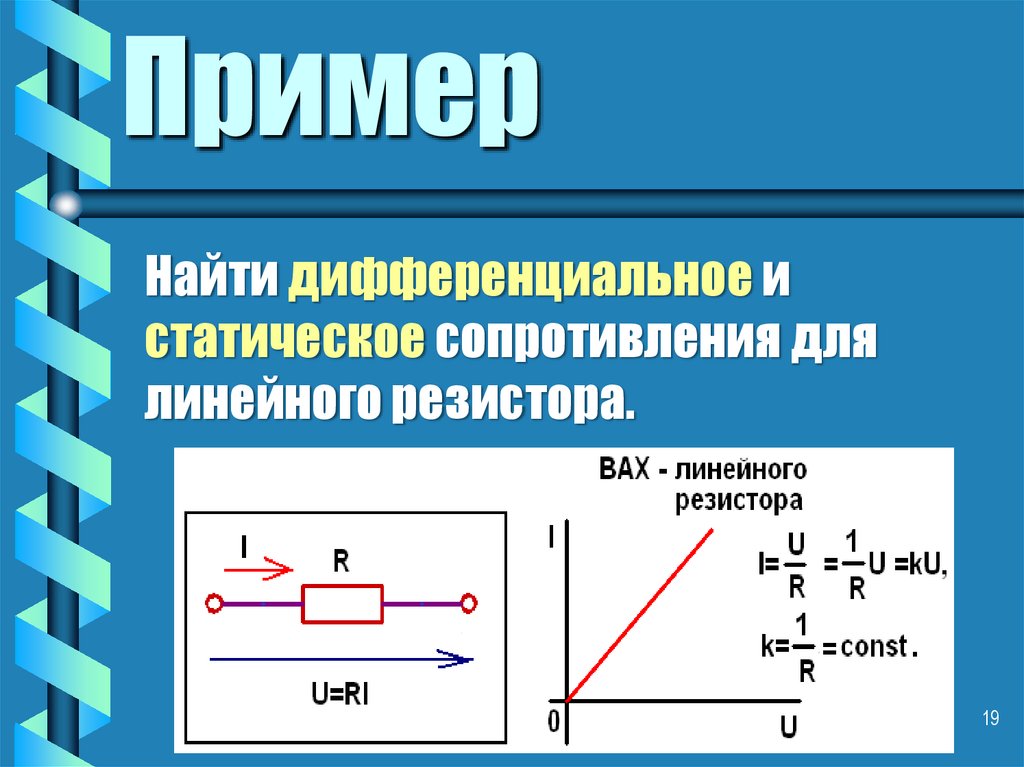
19. Пример
Найти дифференциальное истатическое сопротивления для
линейного резистора.
19
20. Решение
2021. Пример
Найти дифференциальноесопротивления
нелинейного элемента с
ВАХ:
2
u=2i +4i+5 в точке I0=1 А.
21
22. Решение
2223. Связь Rd и RCT
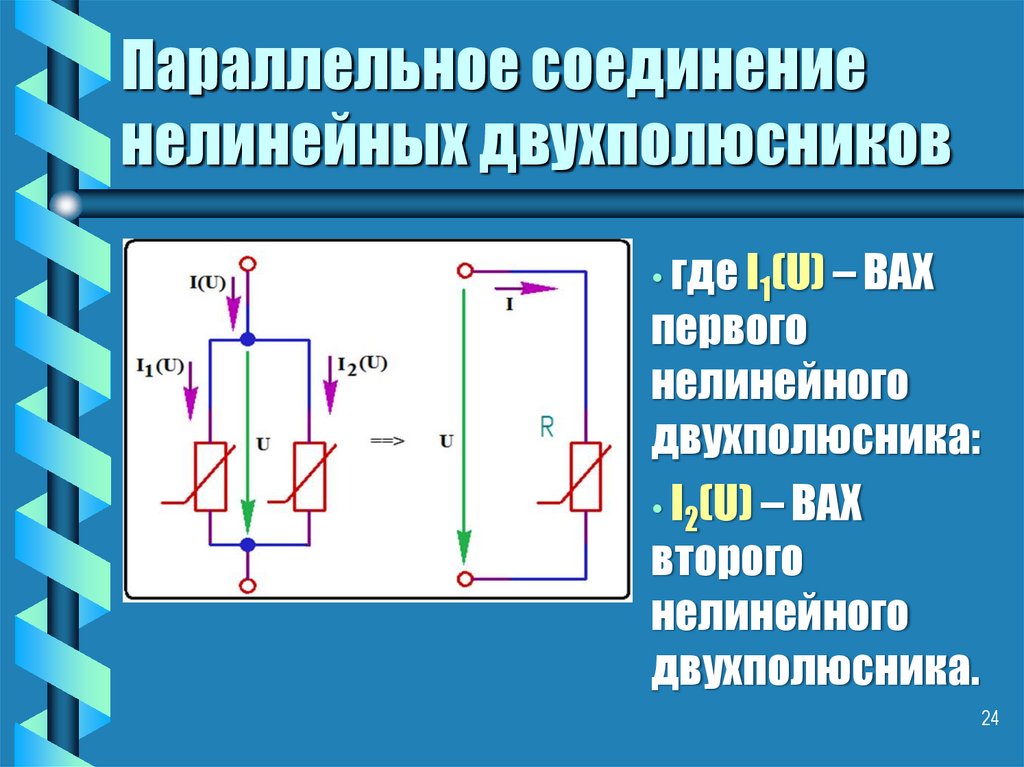
2324. Параллельное соединение нелинейных двухполюсников
• где I1(U) – ВАХпервого
нелинейного
двухполюсника:
• I2(U) – ВАХ
второго
нелинейного
двухполюсника.
24
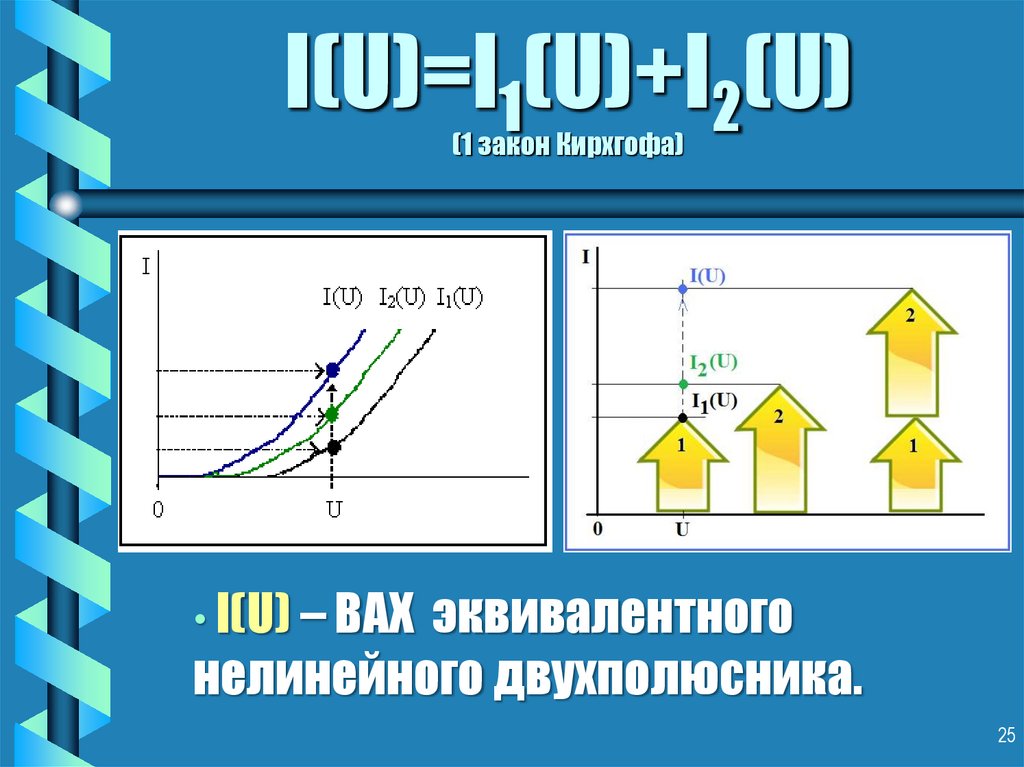
25. I(U)=I1(U)+I2(U) (1 закон Кирхгофа)
• I(U) – ВАХ эквивалентногонелинейного двухполюсника.
25
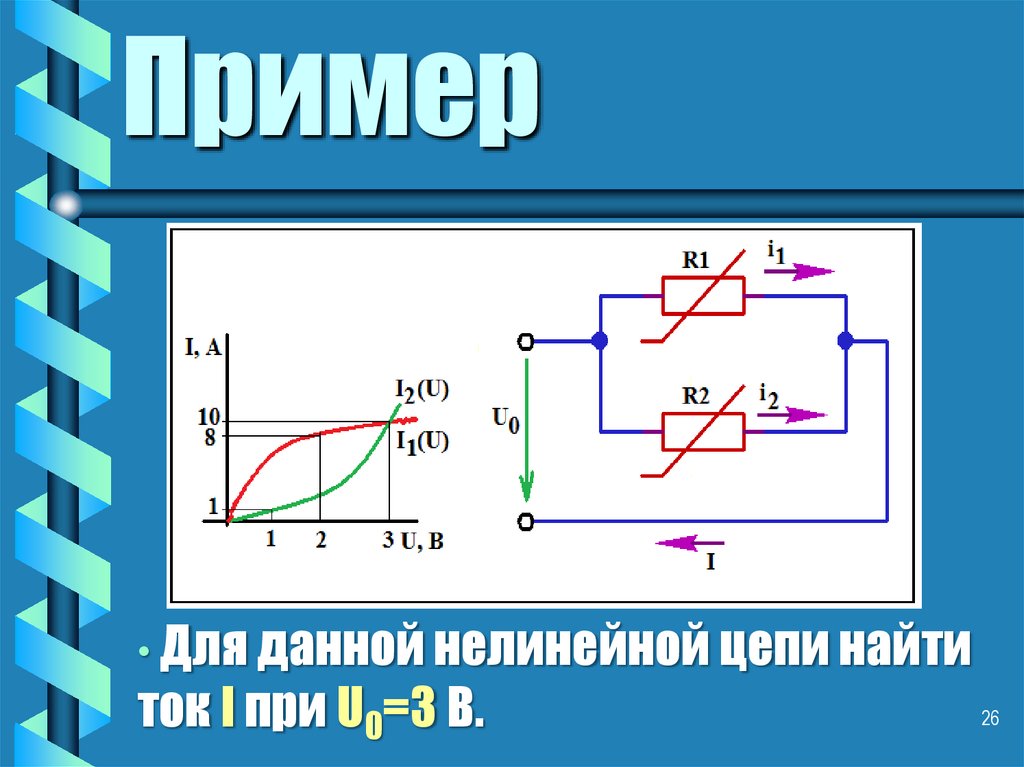
26. Пример
• Для данной нелинейной цепи найтиток I при U0=3 В.
26
27. Решение
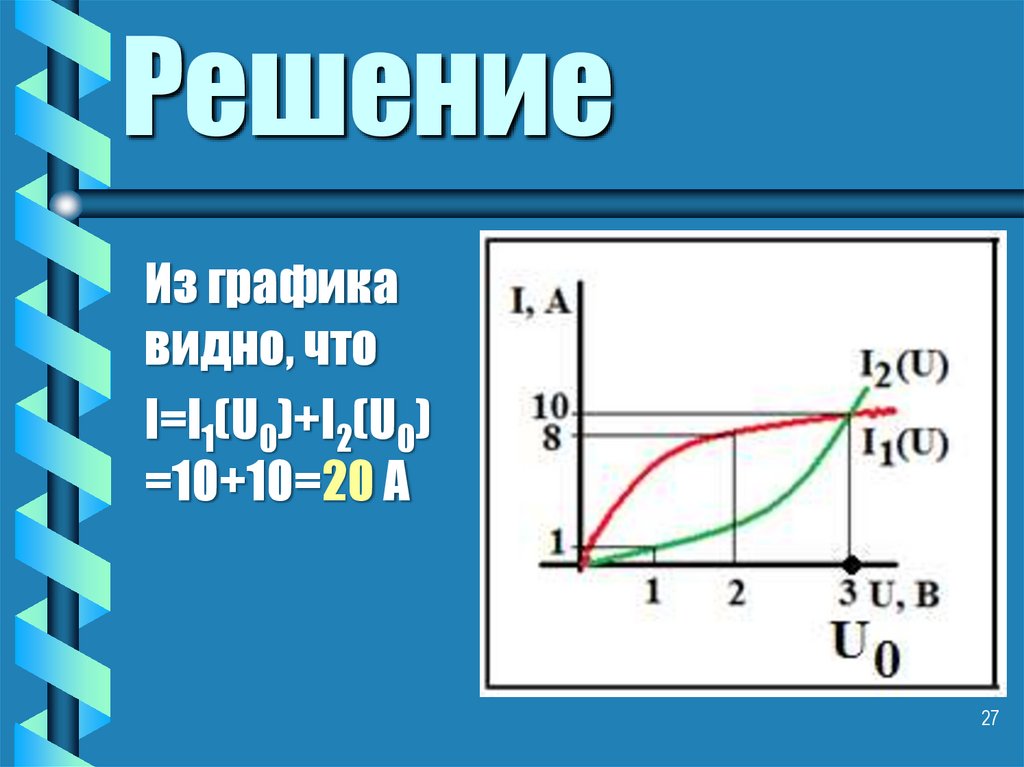
Из графикавидно, что
I=I1(U0)+I2(U0)
=10+10=20 А
27
28. Пример
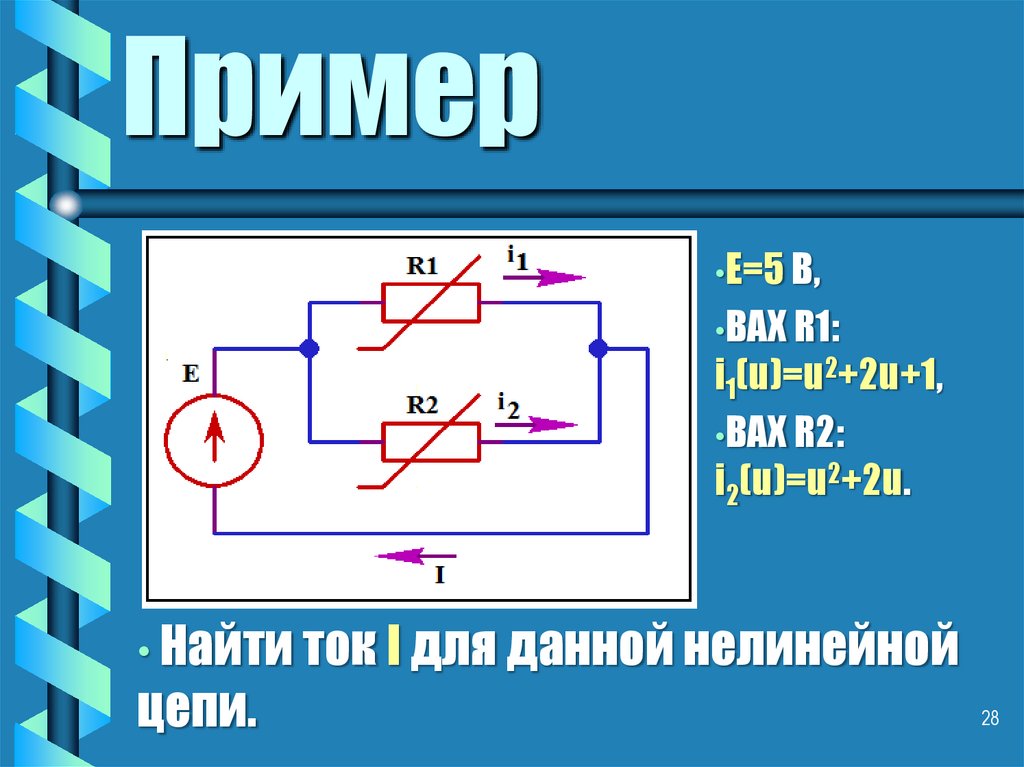
•Е=5 В,•ВАХ R1:
i1(u)=u2+2u+1,
•ВАХ R2:
i2(u)=u2+2u.
• Найти ток I для данной нелинейной
цепи.
28
29. Решение
Найдём токиз первого закона Кирхгофа
I=i1(E)+i2(E)=52+2*5+1+ 52+2*5=71 А.
29
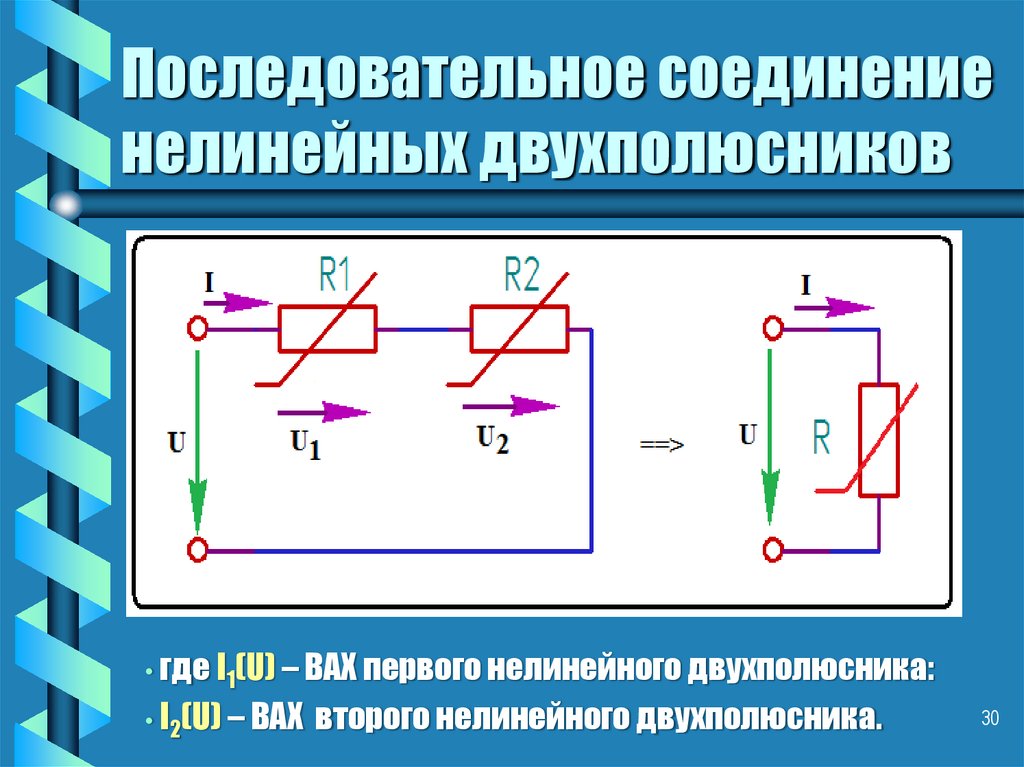
30. Последовательное соединение нелинейных двухполюсников
• где I1(U) – ВАХ первого нелинейного двухполюсника:• I2(U) – ВАХ второго нелинейного двухполюсника.
30
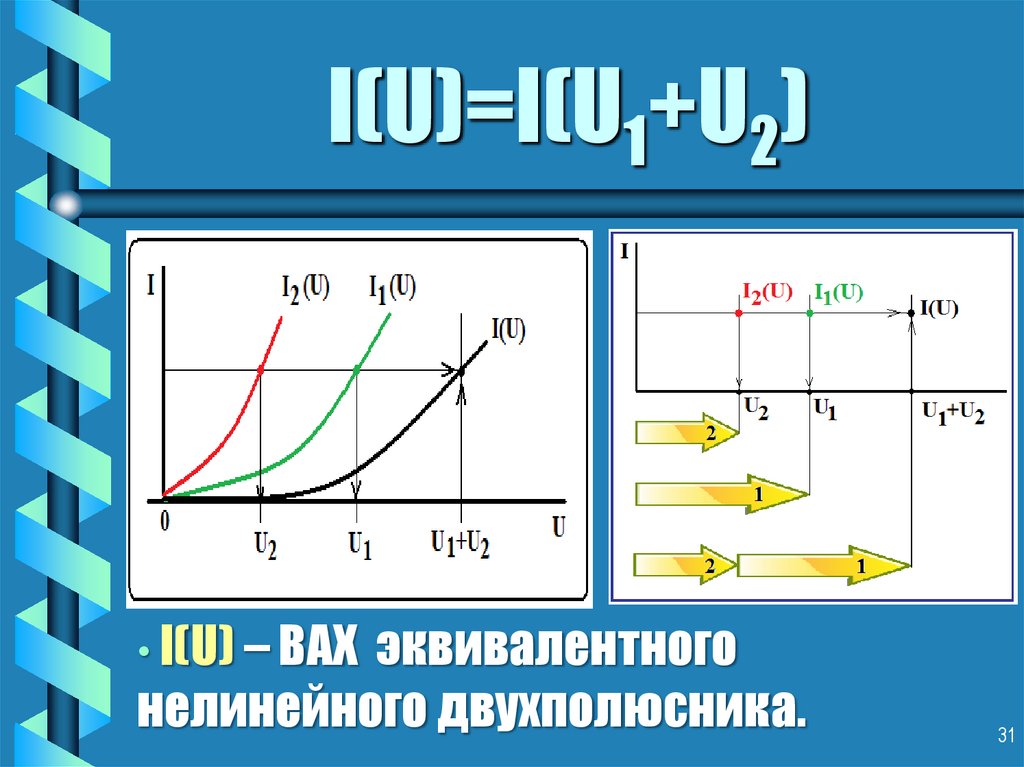
31. I(U)=I(U1+U2)
• I(U) – ВАХ эквивалентногонелинейного двухполюсника.
31
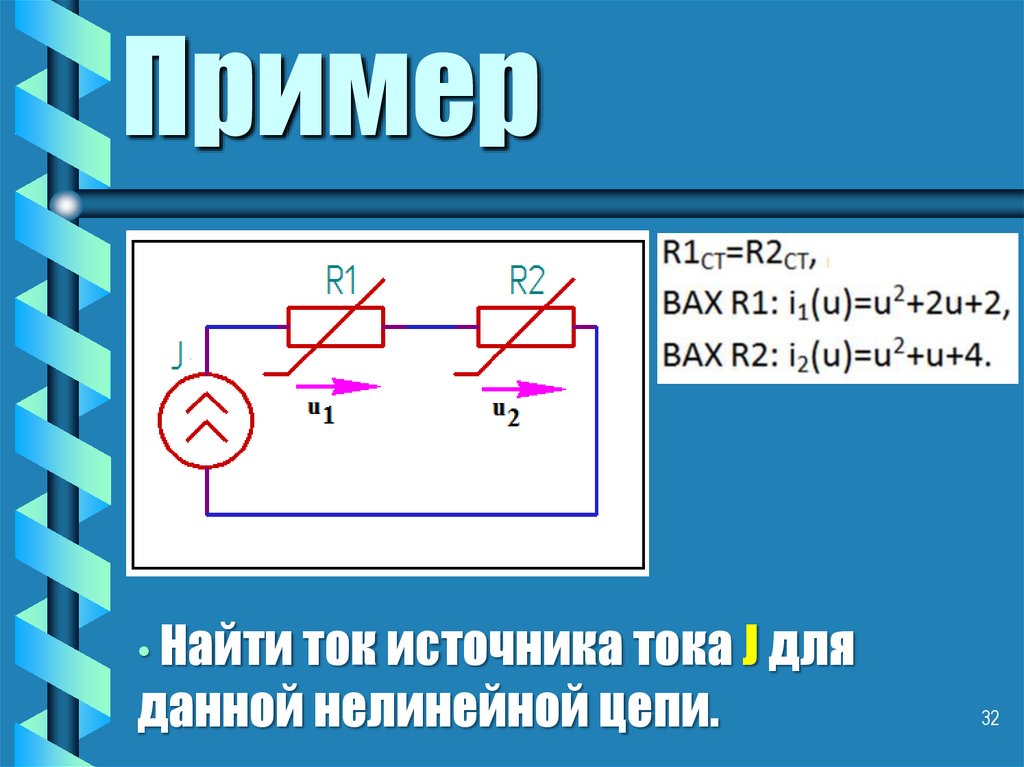
32. Пример
• Найти ток источника тока J дляданной нелинейной цепи.
32
33. Решение
3334. Ответ
3435. Корректирующие цепи
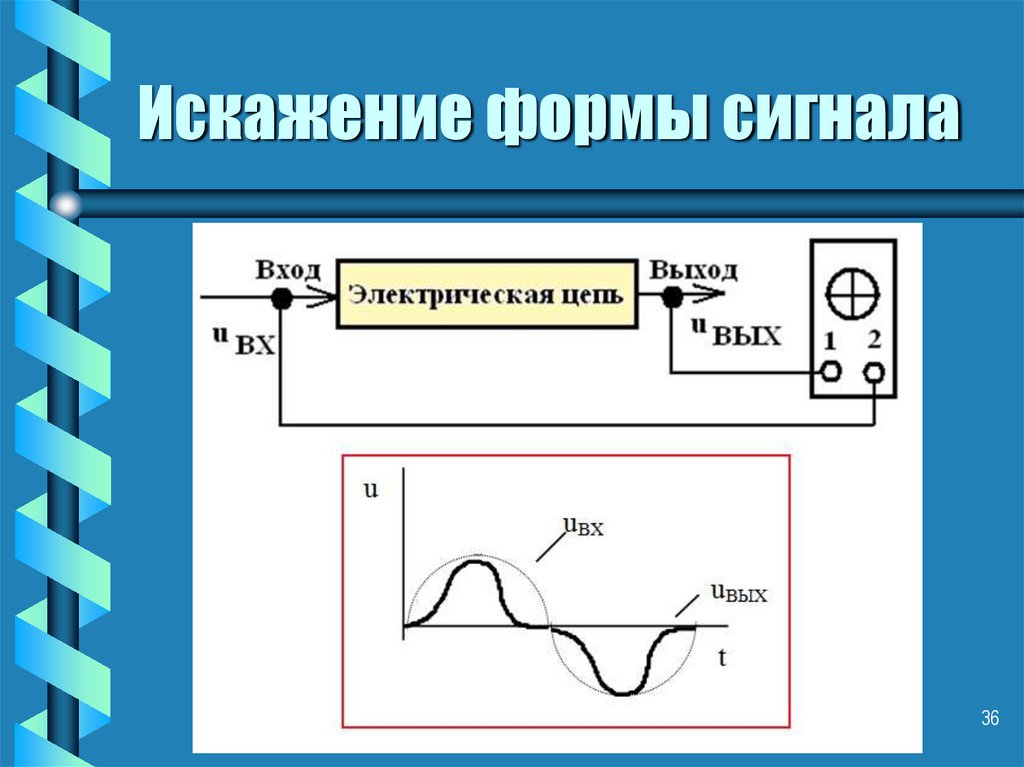
• При прохождении сигналачерез электрические цепи
как активные, так и
пассивные может
происходить искажения
его формы.
35
36. Искажение формы сигнала
3637. Измерение искажений
• Небольшие искажениязаметить на экране
осциллографа очень трудно,
поэтому на выход цепи
подключают измеритель
коэффициента гармоник.
37
38. Искажения формы сигналов
• Одним из методов для расчёталинейных искажений часто
применяемый для оценки
активных цепей, например,
усилителя, работающего в
линейном режиме является метод
испытания прямоугольными
импульсами.
38
39. Метод испытания прямоугольными импульсами
• Пусть на вход линейного усилителяподается меандр с частотой
следования f=1 кГц.
39
40. Метод испытания прямоугольными импульсами
На экране осциллографа изображение
меандра будет неискаженным только
в том случае, если частотные
составляющие меандра пройдут через
активную цепь неискажёнными, т.е. не
испытают ни частотных
(амплитудных), ни фазовых искажений.
40
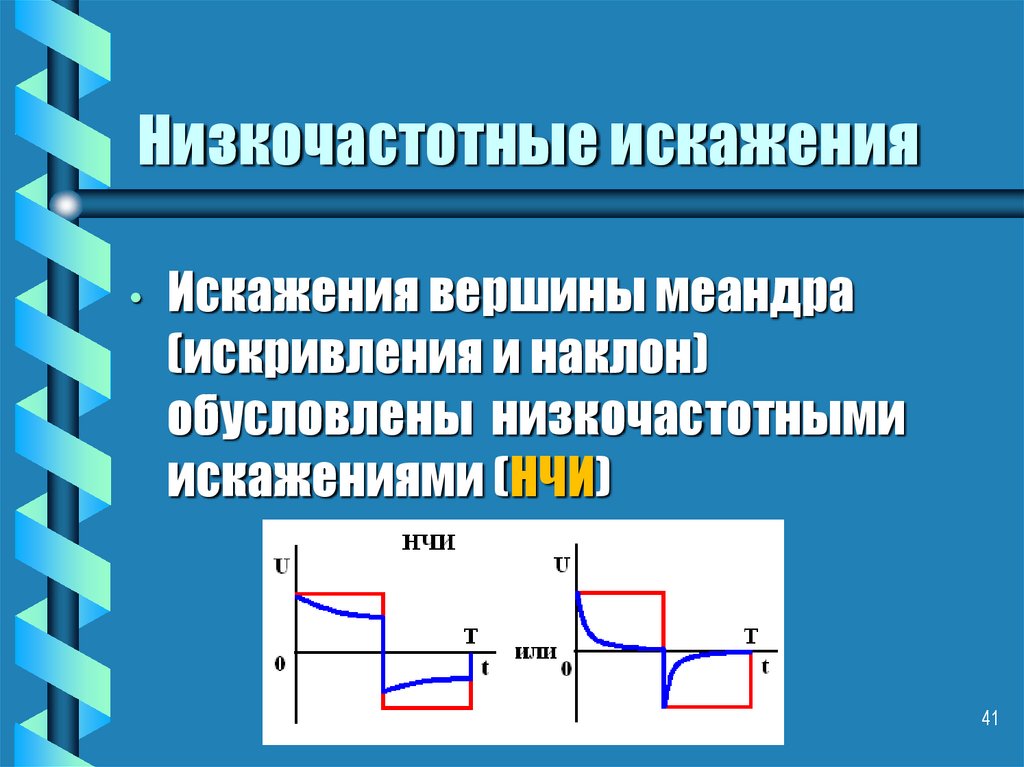
41. Низкочастотные искажения
• Искажения вершины меандра(искривления и наклон)
обусловлены низкочастотными
искажениями (НЧИ)
41
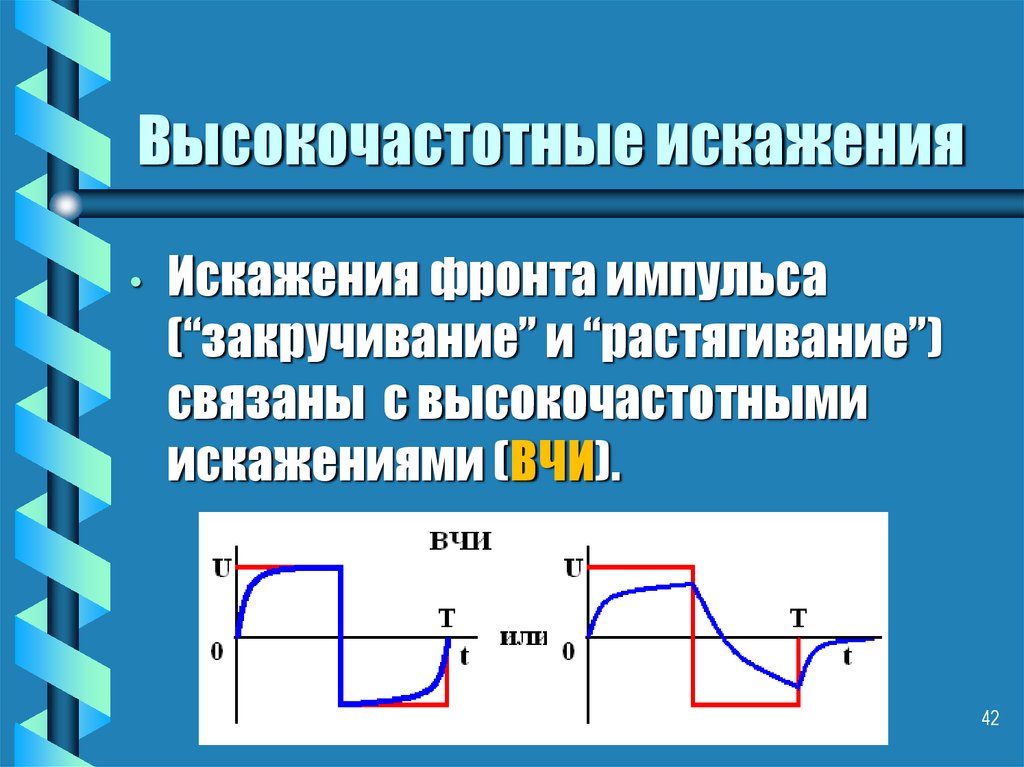
42. Высокочастотные искажения
• Искажения фронта импульса(“закручивание” и “растягивание”)
связаны с высокочастотными
искажениями (ВЧИ).
42
43. Аплитудно-частотные искажения
• Если искажения формы сигнала навыходе активной цепи вызвано
неравномерностью АЧХ цепи в
пределах рабочей полосы частот ,
то такие искажения называются
амплитудно-частотными
искажениями (АЧИ).
43
44. Величина АЧИ
H0a( 0 ) 20 lg
H
(
)
0
• Где a( 0), дБ – величина АЧИ на частоте 0;
• H0 – значение АЧХ в области средних частот;
• H( 0) – значение АЧХ на частоте 0.
44
45. Фазочастотные искажения
• Если искажения формы сигнала,вызванные нелинейностью ФЧХ
цепи и связанны с
неодинаковостью фазовой
скоростью гармоник, то такие
искажения называются
фазочастотными искажениями
(ФЧИ).
45
46. Корректирующие цепи
• Для уменьшения искаженияиспользуют активные и
пассивные
корректирующие
четырёхполюсники (КЧ).
46
47. Амплитудные и фазовые корректоры
Одним КЧ можно скомпенсировать как
амплитудные, так и фазовые
искажения. Однако практически
раздельную коррекцию выполнять
проще, поэтому чаще всего
корректирование проводят раздельно с
помощью амплитудных корректоров
(АК) и фазовых корректоров (ФК).
47
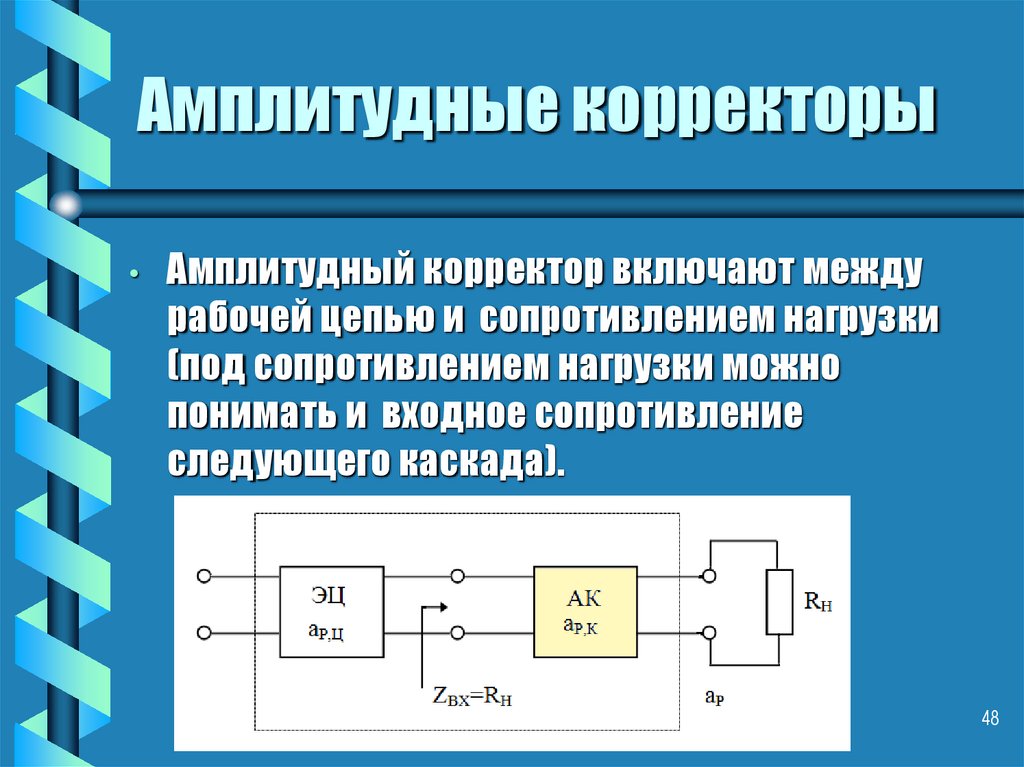
48. Амплитудные корректоры
Амплитудный корректор включают между
рабочей цепью и сопротивлением нагрузки
(под сопротивлением нагрузки можно
понимать и входное сопротивление
следующего каскада).
48
49. Рабочее ослабление
Подбором параметров АК можнодобиться постоянства рабочего
ослабления всей цепи.
• aP = aP,Ц + aP,К =const.
• Выполнение этого условия означает
отсутствие амплитудно-частотных
искажений в рабочей полосе частот.
49
50. Рабочее ослабление АК
Требуемое ослабление АК определяется как
разность между ослаблением всей цепи aP и
ослаблением рабочей цепи для каждой
частоты рабочей полосы частот.
aP - aP,Ц = aP,К
50
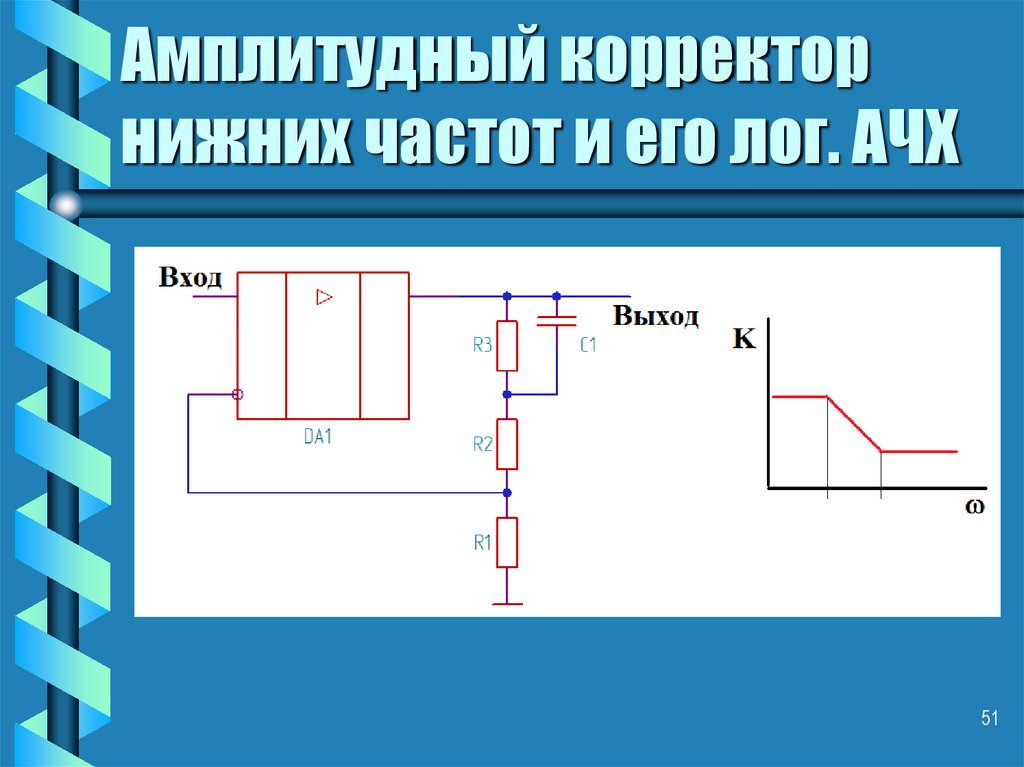
51. Амплитудный корректор нижних частот и его лог. АЧХ
5152. Фазовые искажения
• Фазовые искажения связаны стем, что в пределах рабочей
полосы частот ФЧХ цепи или
канала передачи сигнала
отличаются от линейной.
52
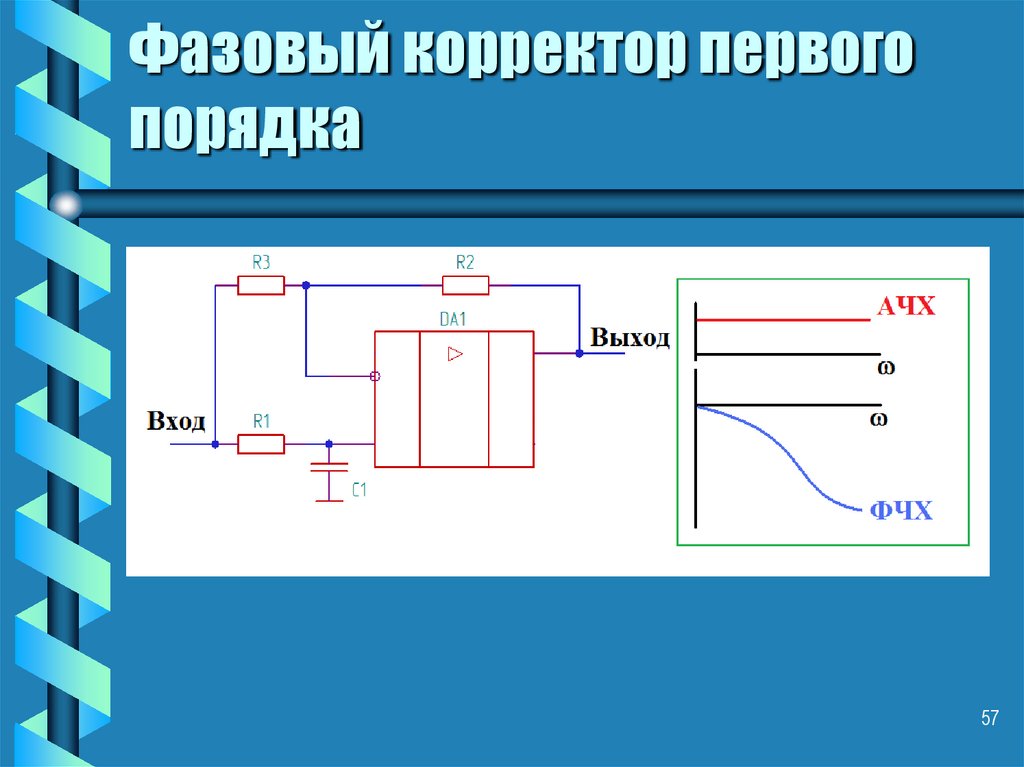
53. Компенсация фазовых искажений
• Для компенсации фазовыхискажений устанавливают
устройства называемые
фазовыми корректорами.
53
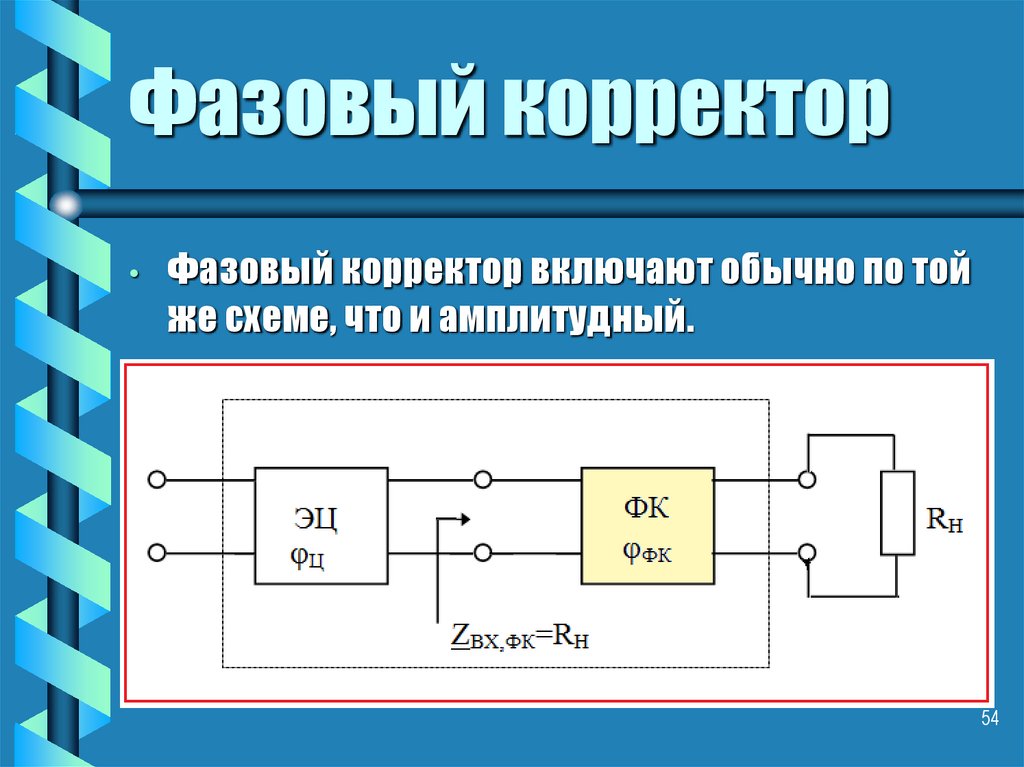
54. Фазовый корректор
Фазовый корректор включают обычно по той
же схеме, что и амплитудный.
54
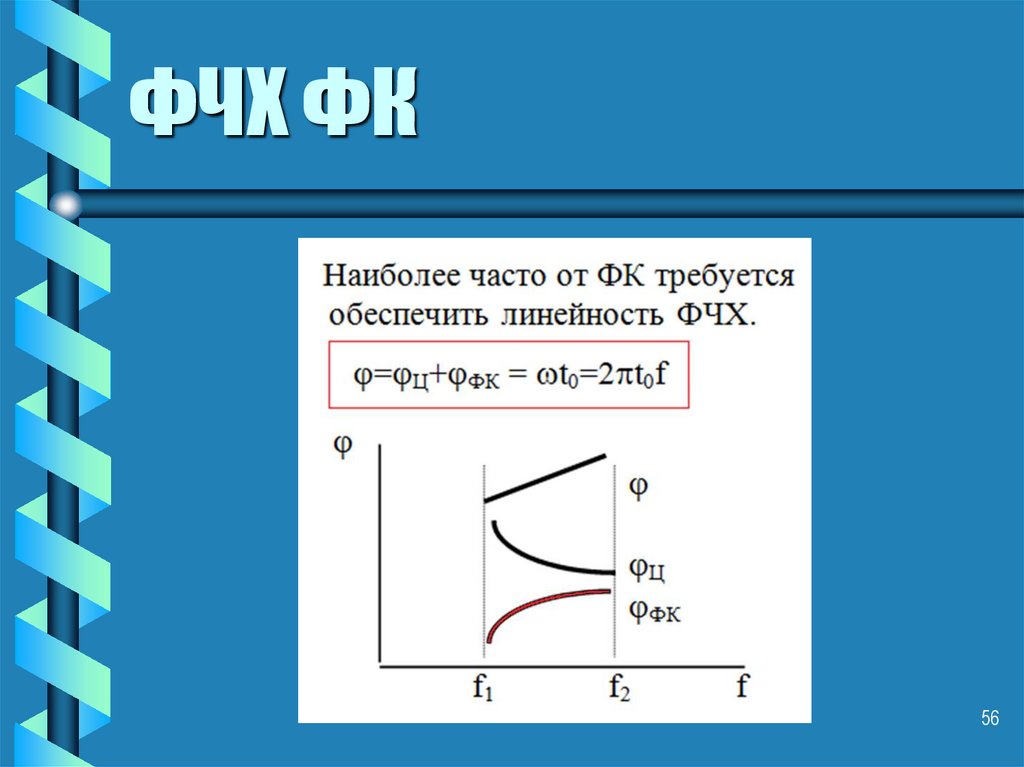
55. Условия
ФК предназначены для формирования требуемой
результирующей ФЧХ, при этом АЧХ не должна
изменяться при подключении фазового корректора,
т.е.
• aР,ФК = 0.
Для выполнения этого условия, очевидно, ФК
должен быть чисто реактивным. Вторым условием
является,
• ZВХ,ФК =RН.
При этих условиях отсутствуют фазовые искажения.
55


































 electronics
electronics








