Similar presentations:
Системы уравнений. Основные понятия
1.
2.
З.2 № 6 Решите уравнение:(х3 – 9х) + (5х2 – 45) = 0
х(х2 – 9) + 5(х2 – 9) = 0
(х2 – 9)(х + 5) = 0
(х – 3)(х + 3)(х + 5) = 0
Произведение равно нулю, когда хотя бы один из
множителей равен нулю, а другие множители при
этом имеют смысл.
х–3=0
х1 = 3
х+3=0
х2 = – 3
Ответ: – 5; – 3; 3.
х+5=0
х3 = – 5
3.
З.2 № 12 Решите уравнение:х2(х + 4) = 9(х + 4)
х2(х + 4) – 9(х + 4) = 0
(х + 4)(х2 – 9) = 0
(х + 4)(х – 3)(х + 3) = 0
Произведение равно нулю, когда хотя бы один из
множителей равен нулю, а другие множители при
этом имеют смысл.
х+4=0
х1 = – 4
х–3=0
х2 = 3
Ответ: – 4; – 3; 3.
х+3=0
х3 = – 3
4.
З.4 № 6 Решите уравнение:(х – 2)(х + 4)2 = 7(х + 4)
(х – 2)(х + 4)2 – 7(х + 4) = 0
(х + 4)((х – 2)(х + 4) – 7) = 0
(х + 4)(х2 + 4х – 2х – 8 – 7) = 0
(х + 4)(х2 + 2х – 15) = 0
Произведение равно нулю, когда хотя бы один из
множителей равен нулю, а другие множители при
этом имеют смысл.
х+4=0
х1 = – 4
х2 + 2х – 15 = 0
По теореме, обратной т. Виета:
Ответ: – 5; – 4; 3.
х2 = – 5
х3 = 3
5.
З.4 № 12 Решите уравнение:(х2 – 49)2 ≥ 0
(х2 + 4х – 21)2 ≥ 0
Значит, чтобы равенство было верным, должно
выполняться условие:
х2 – 49 = 0 · (– 1)
+
х2 + 4х – 21 = 0
– х2 + 49 = 0
х2 + 4х – 21 = 0
4х + 28 = 0
4х = – 28
х=–7
Ответ: – 7.
6.
З.4 № 4 Решите уравнение:(х + 3)(4х + 2)2 – (4х + 2)(х + 3)2 = 0
(х + 3)(4х + 2)((4х + 2) – (х + 3)) = 0
(х + 3)(4х + 2)(4х + 2 – х – 3) = 0
(х + 3)(4х + 2)(3х – 1) = 0
Произведение равно нулю, когда хотя бы один из
множителей равен нулю, а другие множители при
этом имеют смысл.
х+3=0
4х + 2 = 0
х1 = – 3
1
х2 =
2
3х – 1 = 0
1
х3 =
3
1 1
Ответ: – 3; ; .
2 3
7.
06.12.2023К л а с с н а я р а б о т а.
Системы уравнений.
Основные понятия.
8.
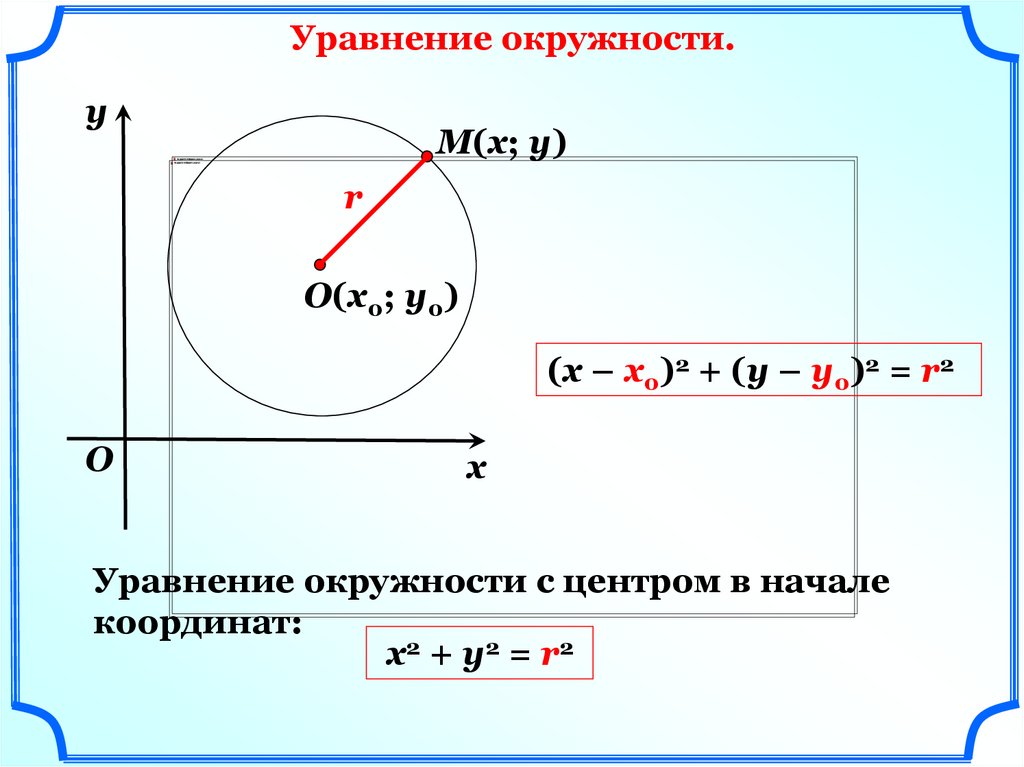
Уравнение окружности.у
М(х; у)
r
О(х0; у0)
(х – х0)2 + (у – у0)2 = r2
О
х
Уравнение окружности с центром в начале
координат:
х 2 + у 2 = r2
9.
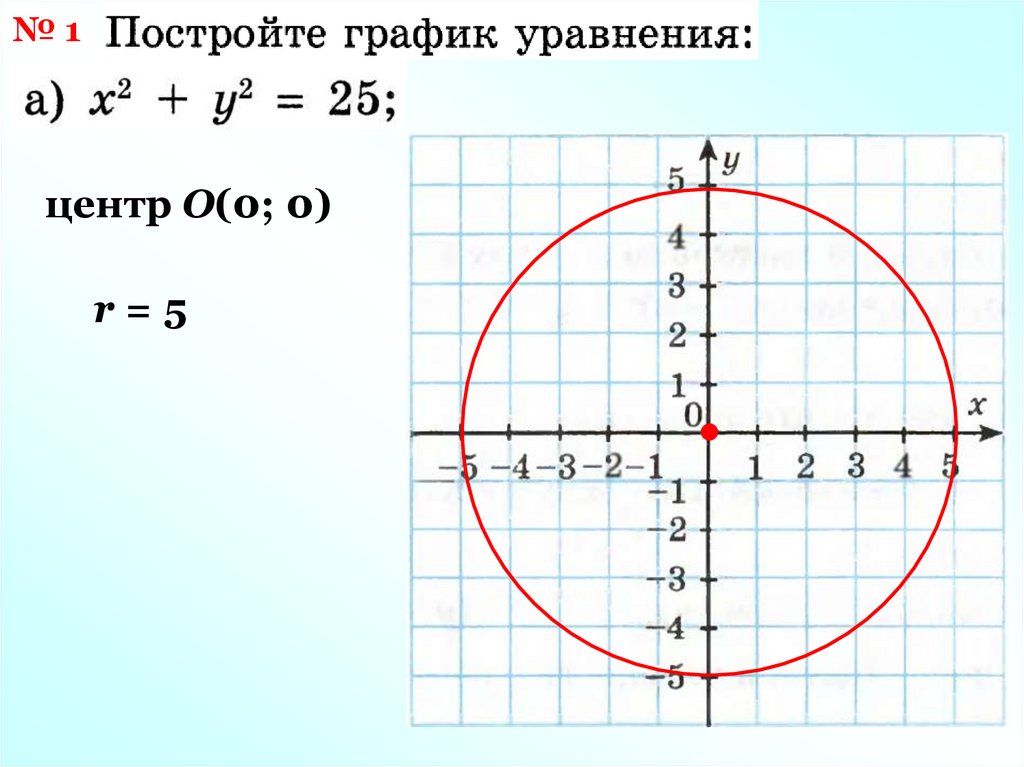
№1центр О(0; 0)
r=5
10.
№2(х – (- 1))2 + (у – 3)2 = 52
центр О(- 1; 3)
r=5
(х – (- 5))2 + (у – ( - 7))2 = 12
центр О(- 5; - 7)
r=1
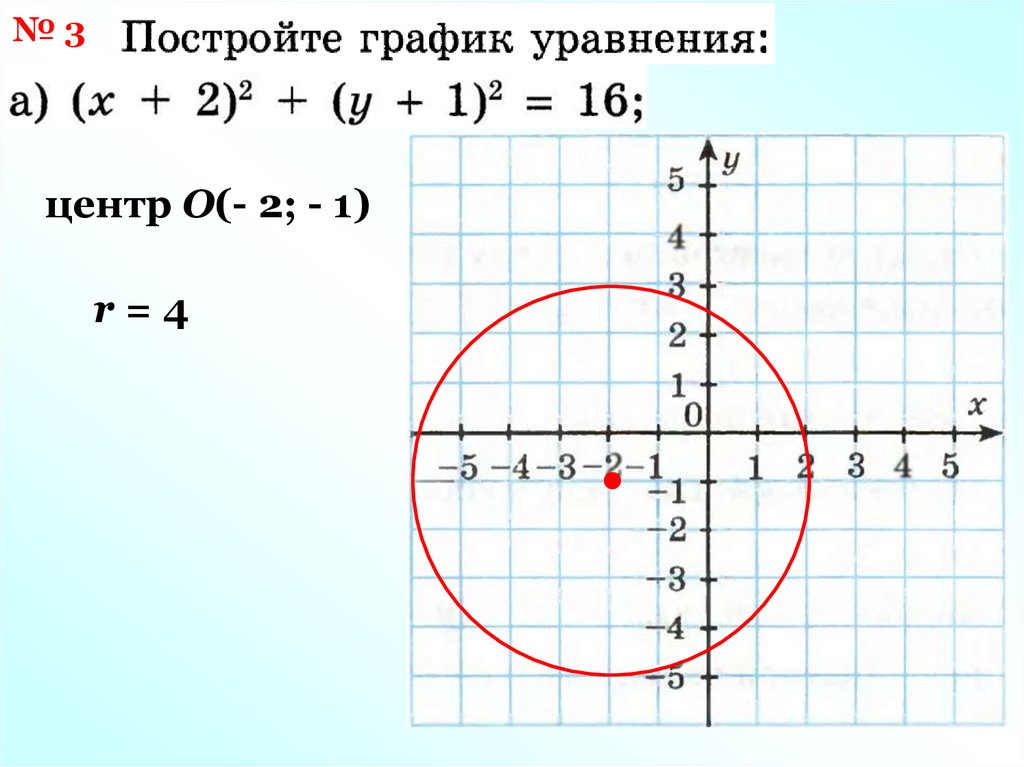
11.
№3центр О(- 2; - 1)
r=4
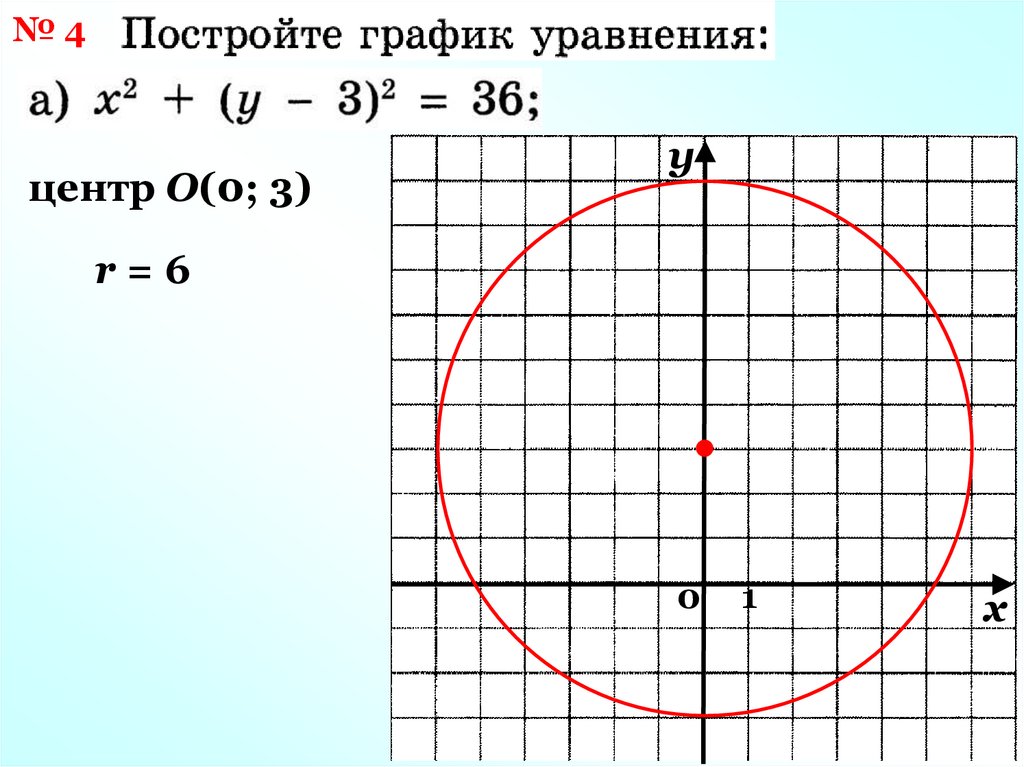
12.
№4центр О(0; 3)
у
r=6
0
1
х
13.
№5(х – хо)2 + (у – уо)2 = r2
(х – 0)2 + (у – 0)2 = 52
х2 + у2 = 25
(х – 0)2 + (у – 0)2 = √32
х2 + у2 = 3
14.
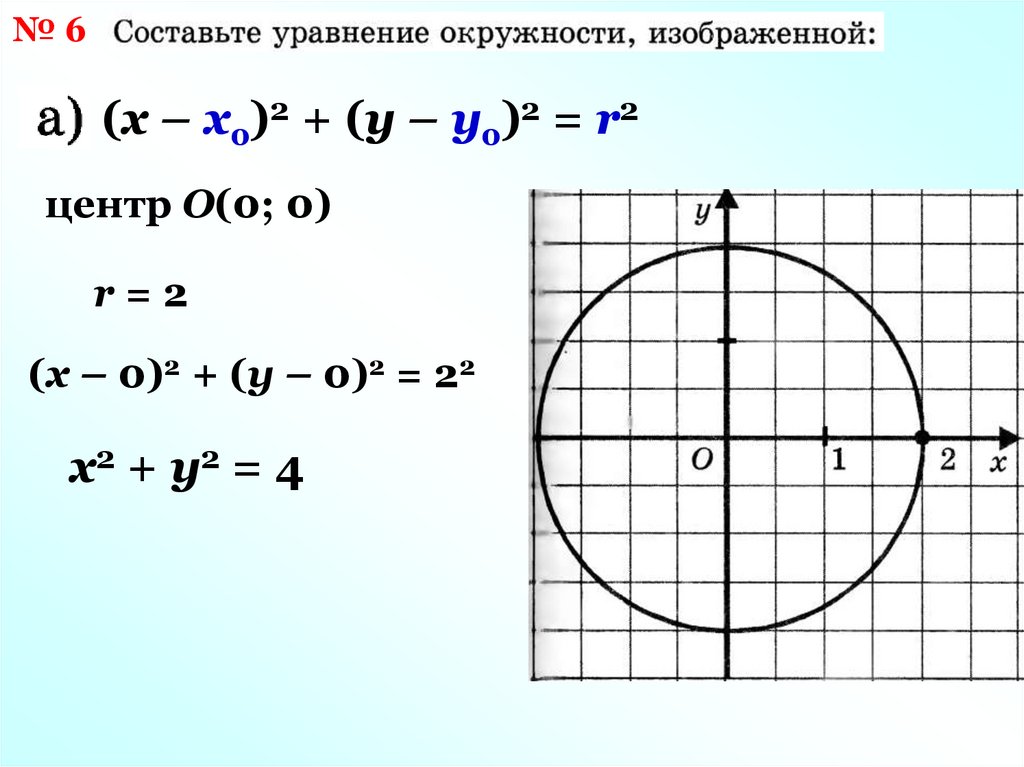
№6(х – хо)2 + (у – уо)2 = r2
центр О(0; 0)
r=2
(х – 0)2 + (у – 0)2 = 22
х2 + у2 = 4
15.
№6(х – хо)2 + (у – уо)2 = r2
центр О(0; 0)
r = √3
(х – 0)2 + (у – 0)2 = √32
х2 + у2 = 3
16.
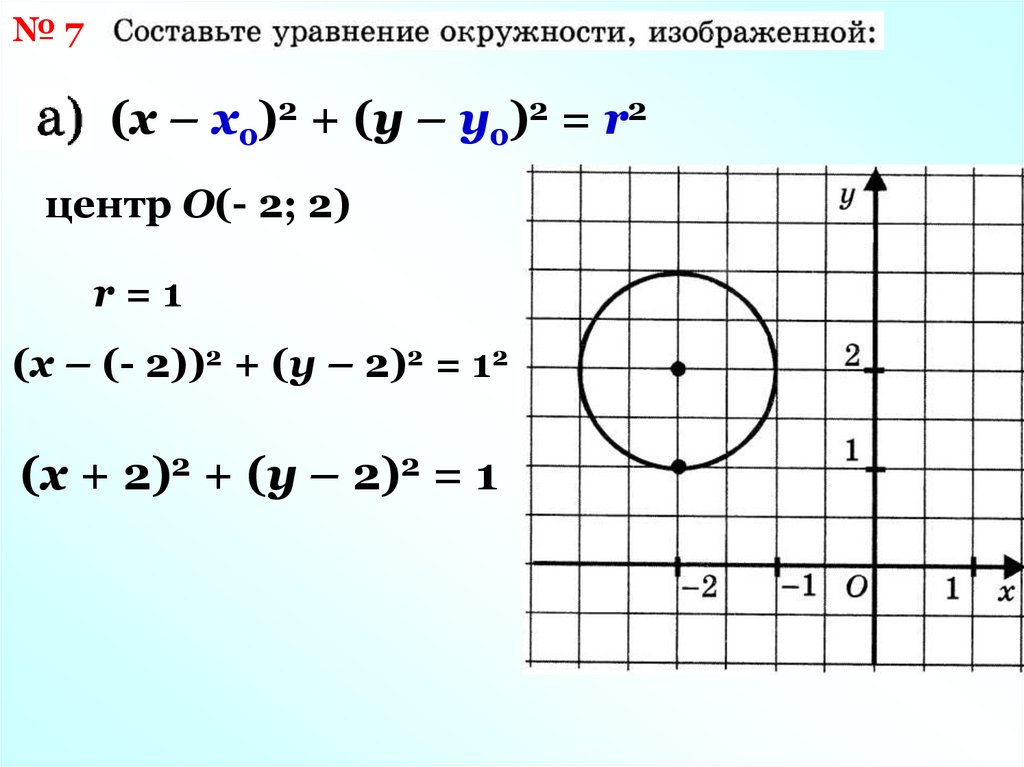
№7(х – хо)2 + (у – уо)2 = r2
центр О(- 2; 2)
r=1
(х – (- 2))2 + (у – 2)2 = 12
(х + 2)2 + (у – 2)2 = 1
17.
№7(х – хо)2 + (у – уо)2 = r2
центр О(3; - 1)
r=2
(х – 3)2 + (у – (- 1))2 = 22
(х – 3)2 + (у + 1)2 = 4
18.
№122 + 32 = 13
2 2+3 = 7
22 + 3 = 5
3 2 - 1 = 3
13 = 13
7 = 7
7 = 5
5 = 3
Ответ: является
Ответ: не является
19.
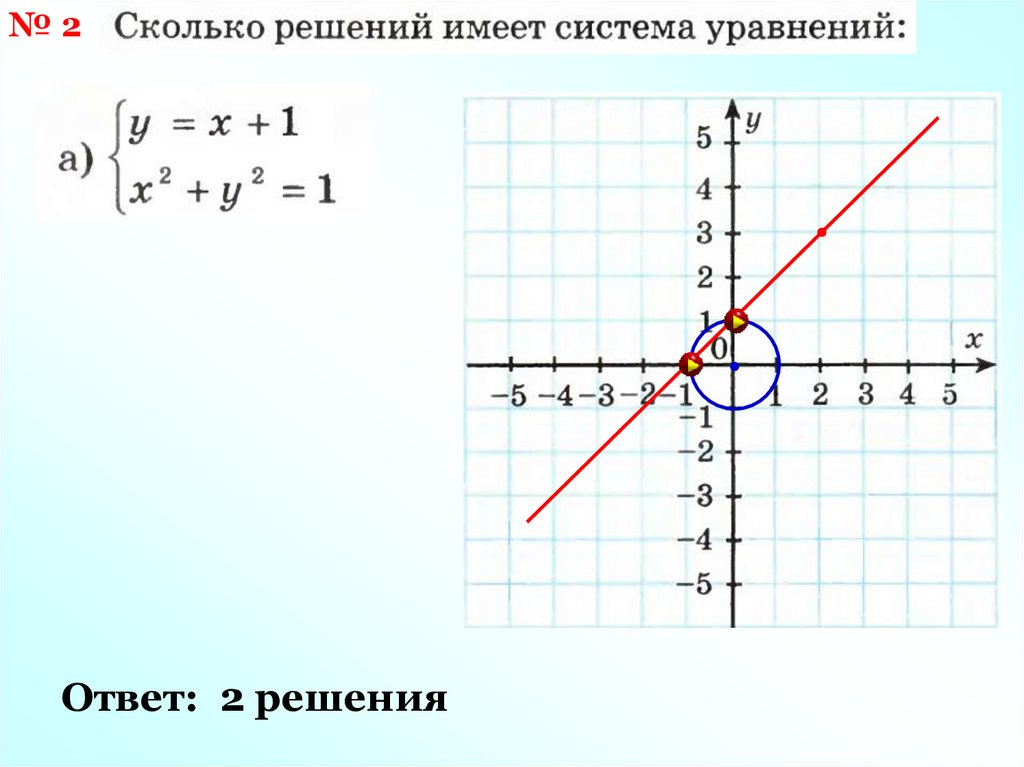
№2Ответ: 2 решения
20.
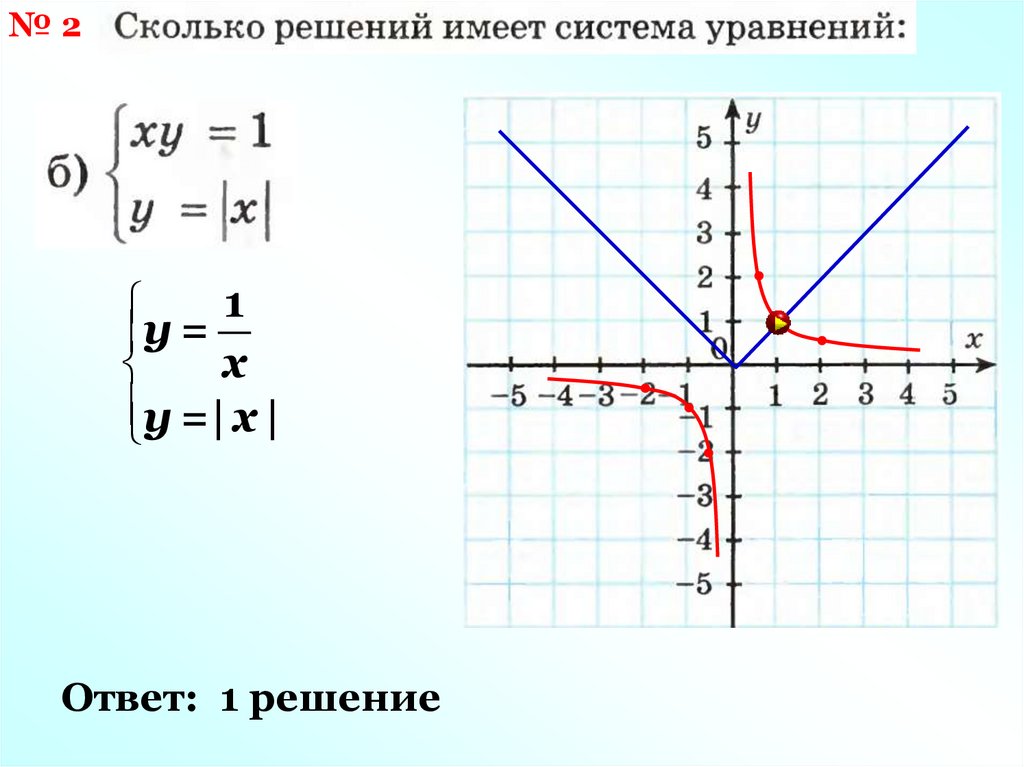
№21
у =
х
у =| х |
Ответ: 1 решение
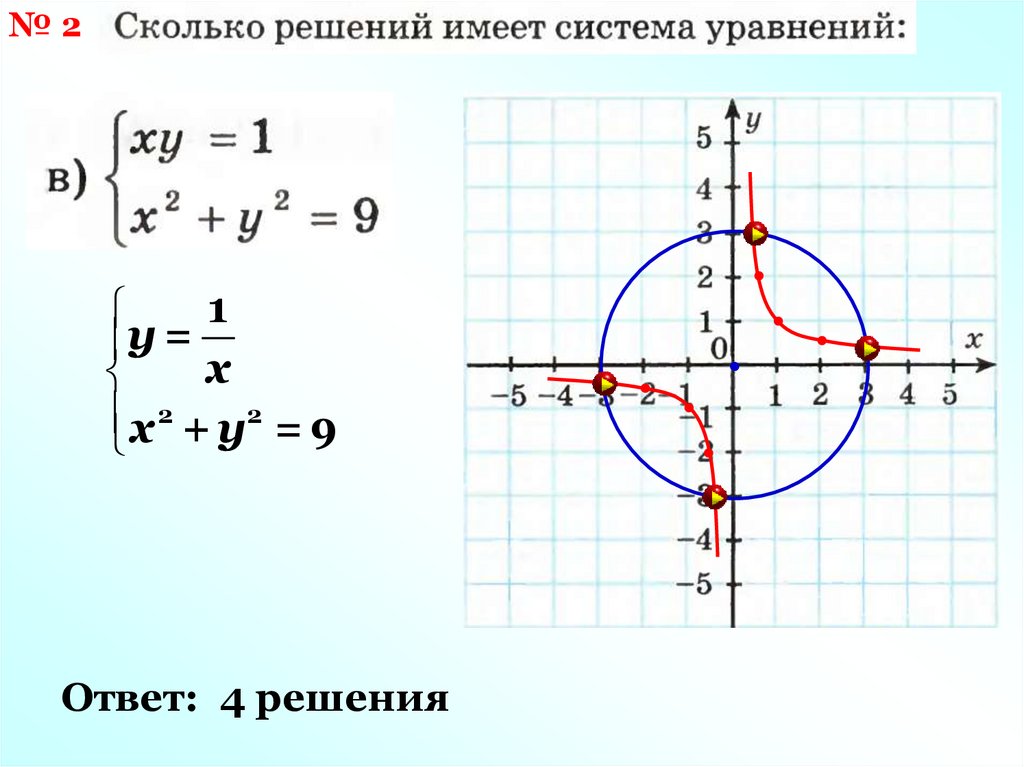
21.
№21
у =
х
х 2 + у2 = 9
Ответ: 4 решения
22.
№2Ответ: 2 решения
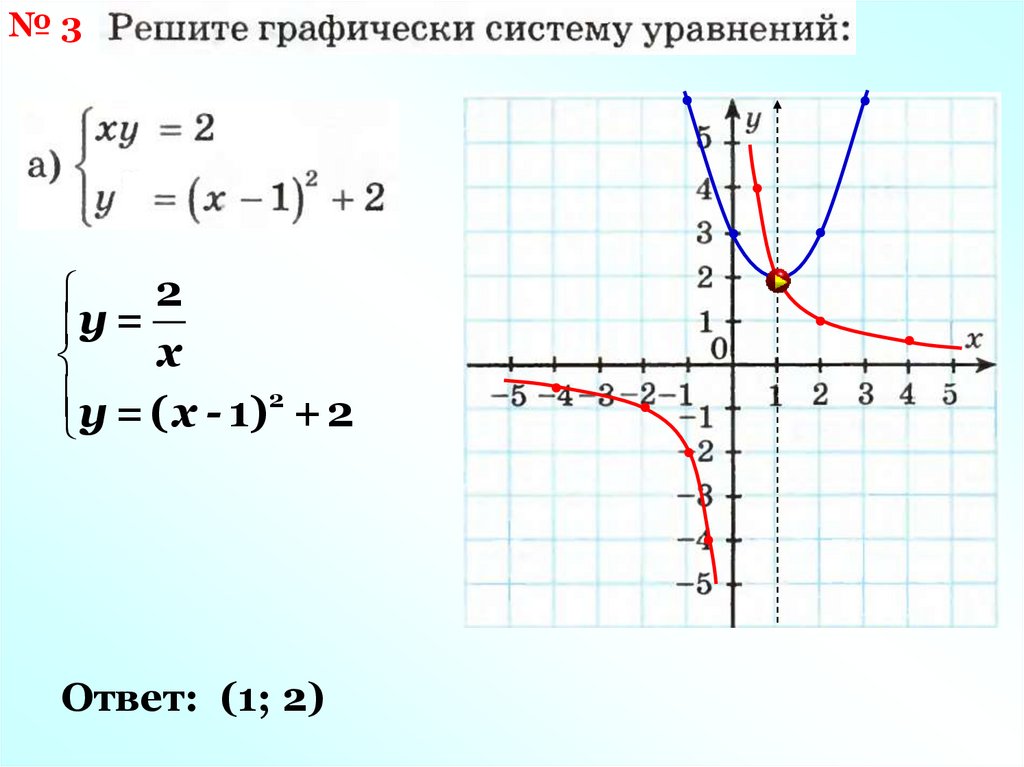
23.
№32
у =
х
у = ( х - 1)2 + 2
Ответ: (1; 2)
24.
№3х 2 +у2 = 4
у = -х - 2
Ответ: (- 2; 0), (0; - 2)
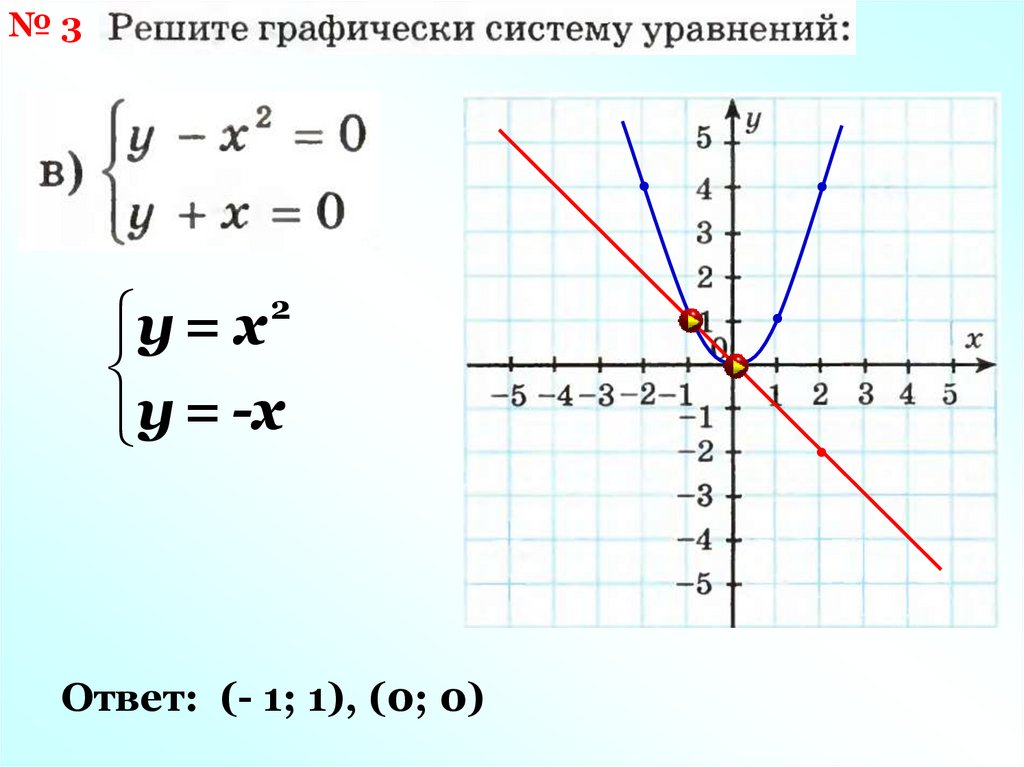
25.
№3у = х
у = -х
2
Ответ: (- 1; 1), (0; 0)
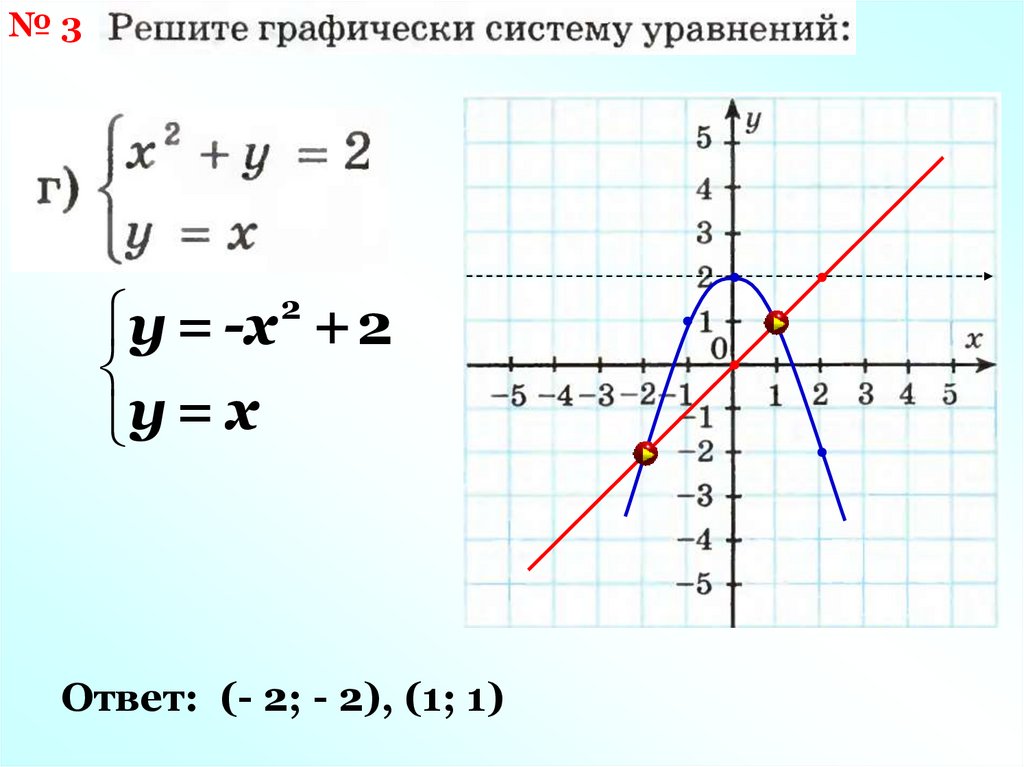
26.
№3у = -х + 2
у = х
2
Ответ: (- 2; - 2), (1; 1)














 mathematics
mathematics








