Терема Пифагора. Древнегреческий философ и математик

1.

Решение задач по теме:
«Терема Пифагора»

2.

Древнегреческий философ
и математик
( VI в до н.э.)-
Пифагор – едва ли не самый
популярный ученый за всю
историю человечества. Вокруг
личности Пифагора
образовалась множество
легенд. Одни называли его
математиком, пророком,
философом, другие
шарлатаном. Судить о
правдивости высказываний
сложно.
Пифагор много
путешествовал, после
возвращения на родину- в
Кротон, начинается самый
славный период его
биографии.

3.

Пифагор основывает школу – пифагорейский союз, состоявший из
молодых представителей аристократии, куда принимались с большими
церемониями после долгих испытаний. Каждый вступающий
отрекался от своего имущества и давал клятву хранить в тайне учения
основателя.

4.

Пифагорейцы занимались математикой, философией, естественными
науками, сделали много важных открытий в арифметике и геометрии. Но
в школе существовал Декрет, по которому авторство всех математических
работ приписывалось Пифагору.

5.

РАЗЛИЧНЫЕ ФОРМУЛИРОВКИ ТЕОРЕМЫ ПИФАГОРА
«В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
(общепризнанная)
Евклид (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над
прямым углом, равен квадратам на сторонах, заключающих прямой
угол".
«Квадрат, построенный на гипотенузе прямоугольного
треугольника, равновелик сумме квадратов, построенных на
катетах». (во времена Пифагора)
В первом русском переводе евклидовых "Начал", сделанном Ф. И.
Петрушевским: "В прямоугольных треугольниках квадрат из
стороны, противолежащей прямому углу, равен сумме квадратов из
сторон, содержащих прямой угол".
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.
): "Во всяком прямоугольном треугольнике квадрат, образованный
на стороне, натянутой над прямым углом, равен сумме двух
квадратов, образованных на двух сторонах, заключающих прямой
угол".

6.

2.
Устный опрос
1. Какой треугольник называется прямоугольным?
2. Чему равна сумма углов прямоугольного треугольника?
3.Чему равна сумма острых углов в прямоугольном треугольнике?
4. Сформулируйте свойство катета, лежащего против угла в 30
градусов.
5. Сформулируйте теорему Пифагора.
6. Как называется сторона противолежащая прямому углу?
7. Как называется сторона прилежащая к прямому углу?

7.

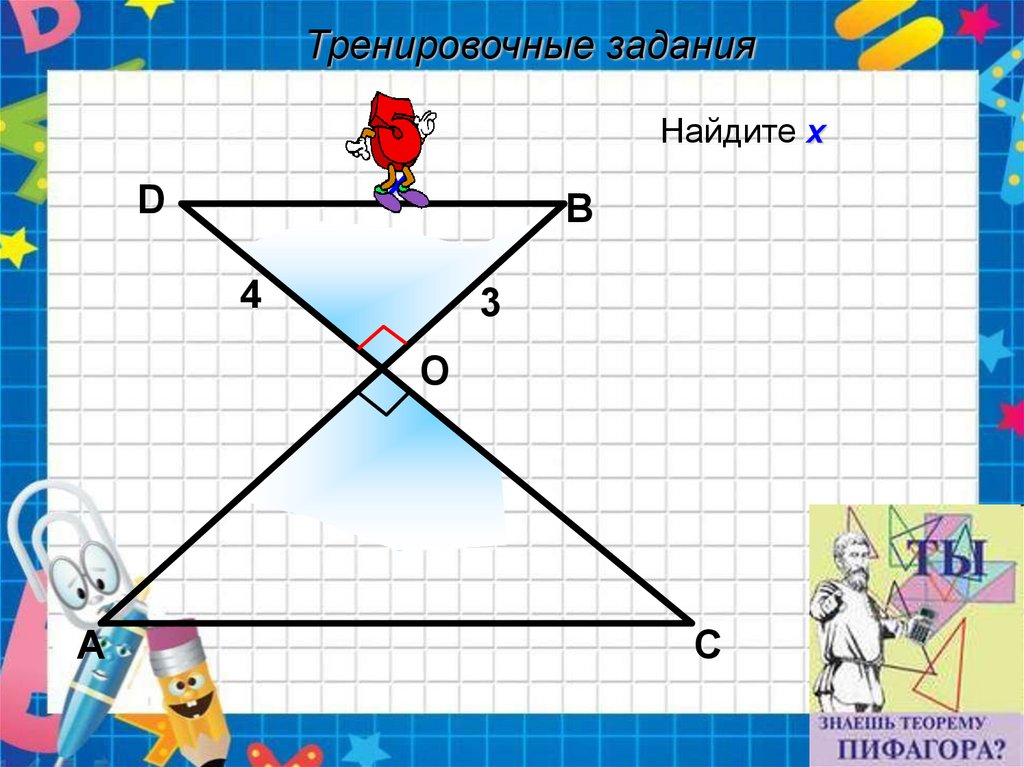
Тренировочные задания
Найдите х
х
D
В
4
3
О
А
С

8.

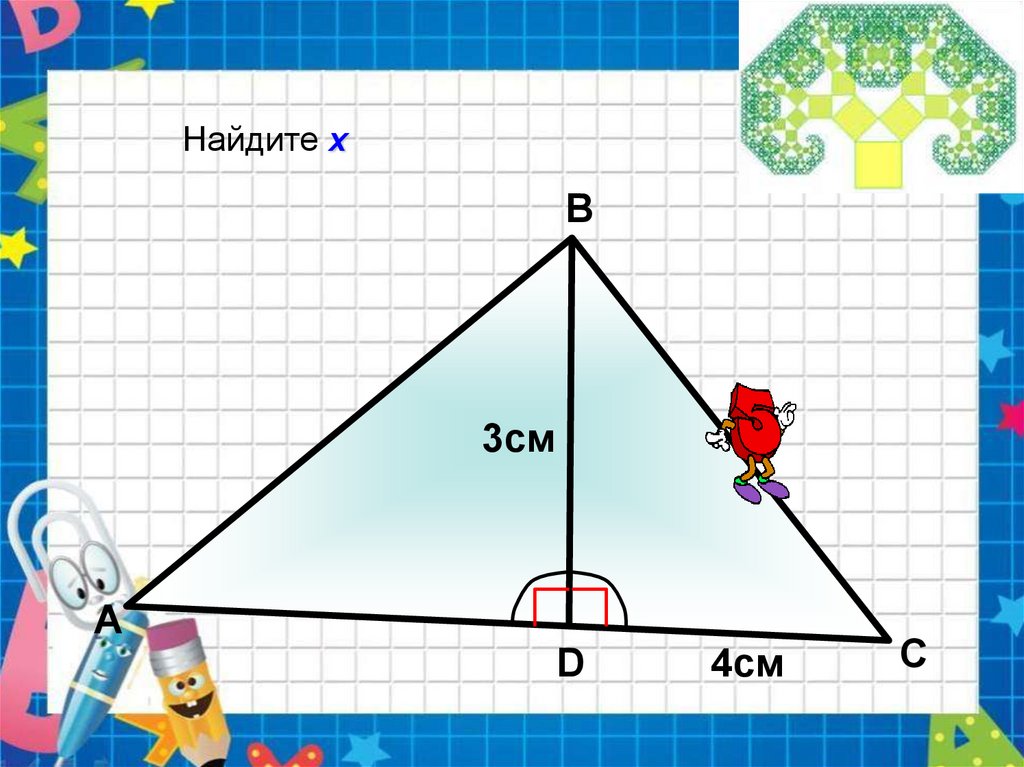
Найдите х
В
х
3см
А
D
4см
С

9.

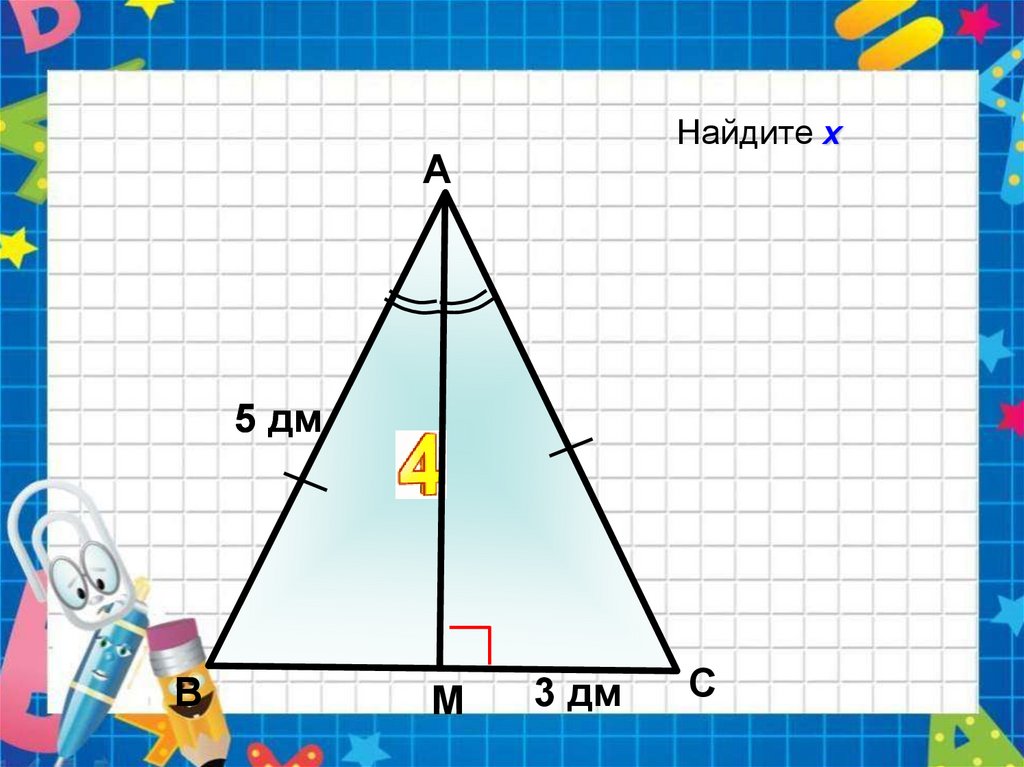
Найдите х
А
5 дм
х
В
М
3 дм
С

10.

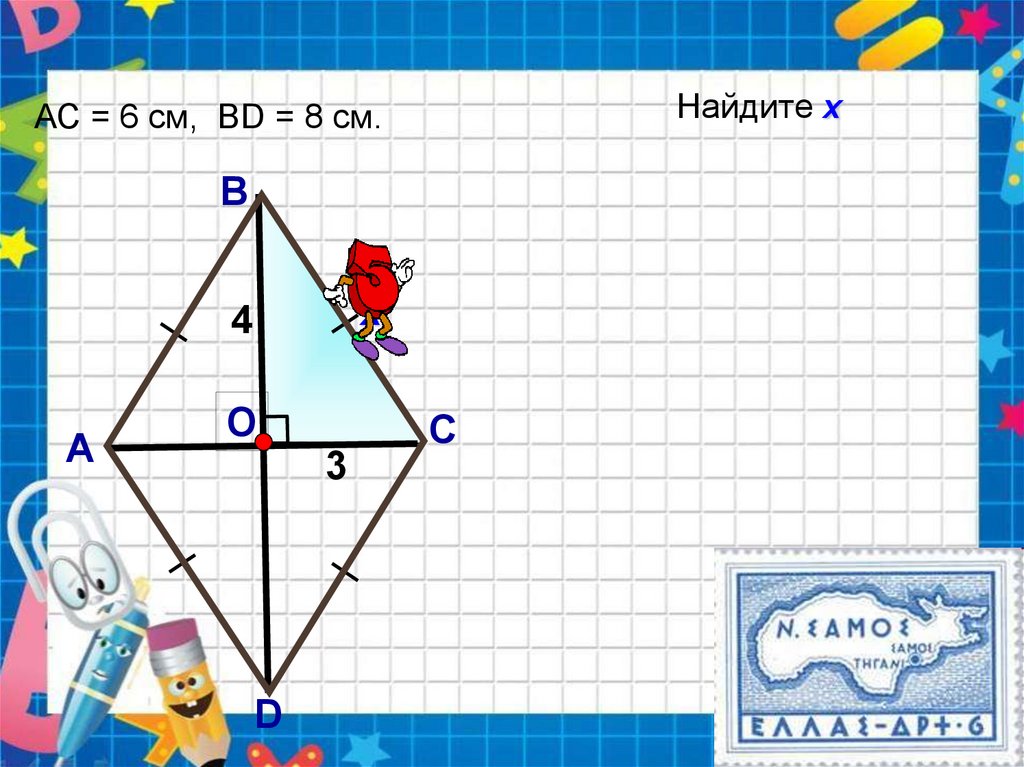
Найдите х
АС = 6 см, ВD = 8 см.
В
х
4
А
О
3
D
С

11.

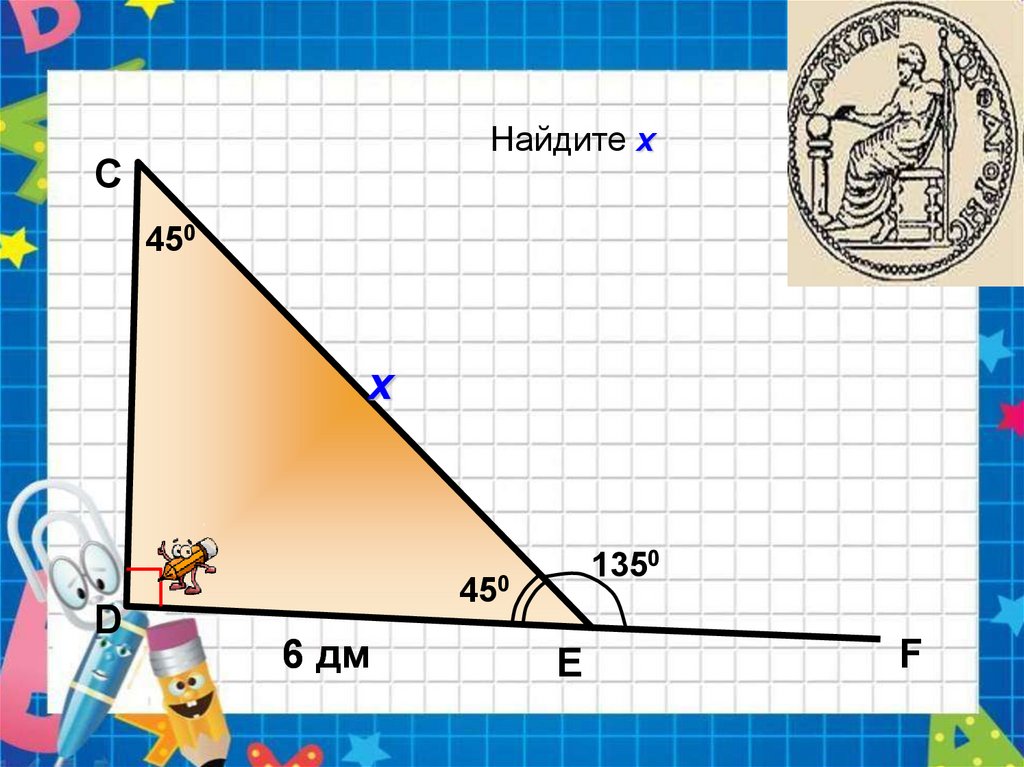
Найдите х
С
450
х
D
1350
450
6 дм
E
F

12.

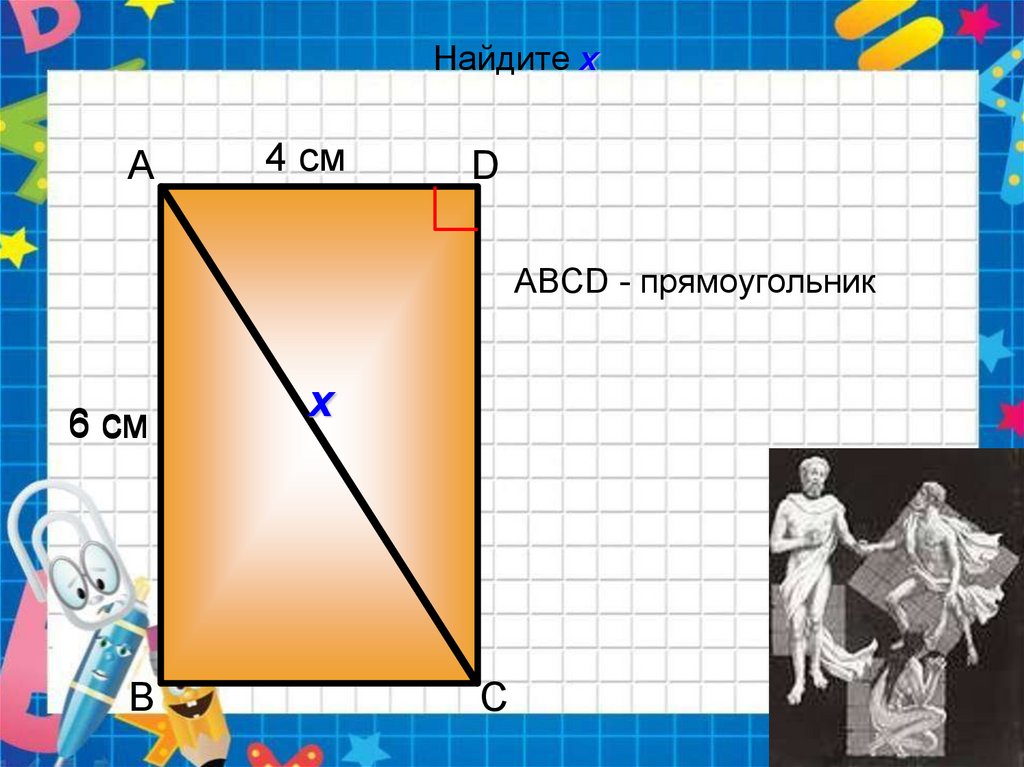
Найдите х
A
4 см
D
АBCD - прямоугольник
6 см
B
х
C

13.

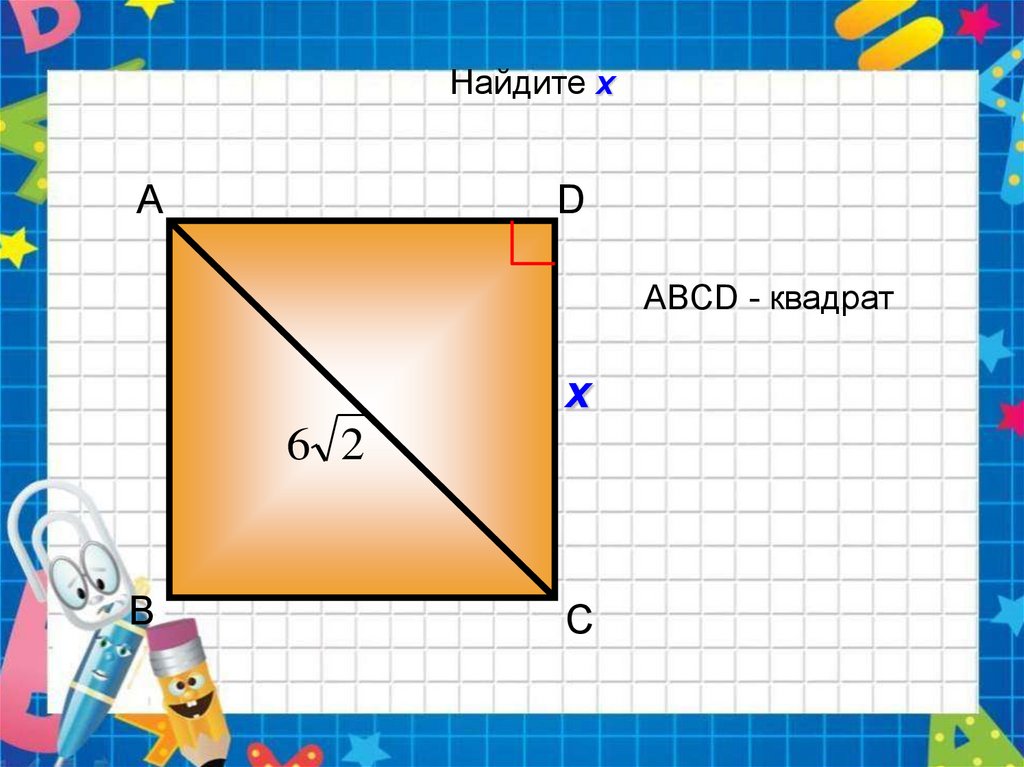
Найдите х
A
D
АBCD - квадрат
х
6 2
B
х
C

14.

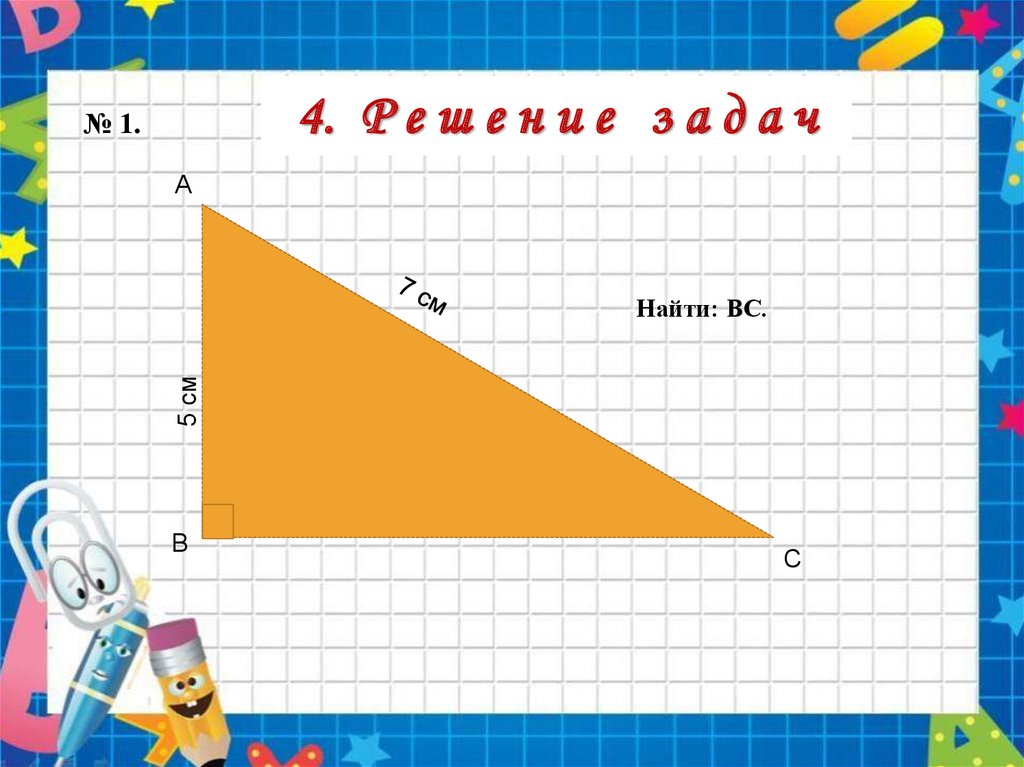
4. Р е ш е н и е з а д а ч
№ 1.
А
5 см
Найти: ВС.
В
С

15.

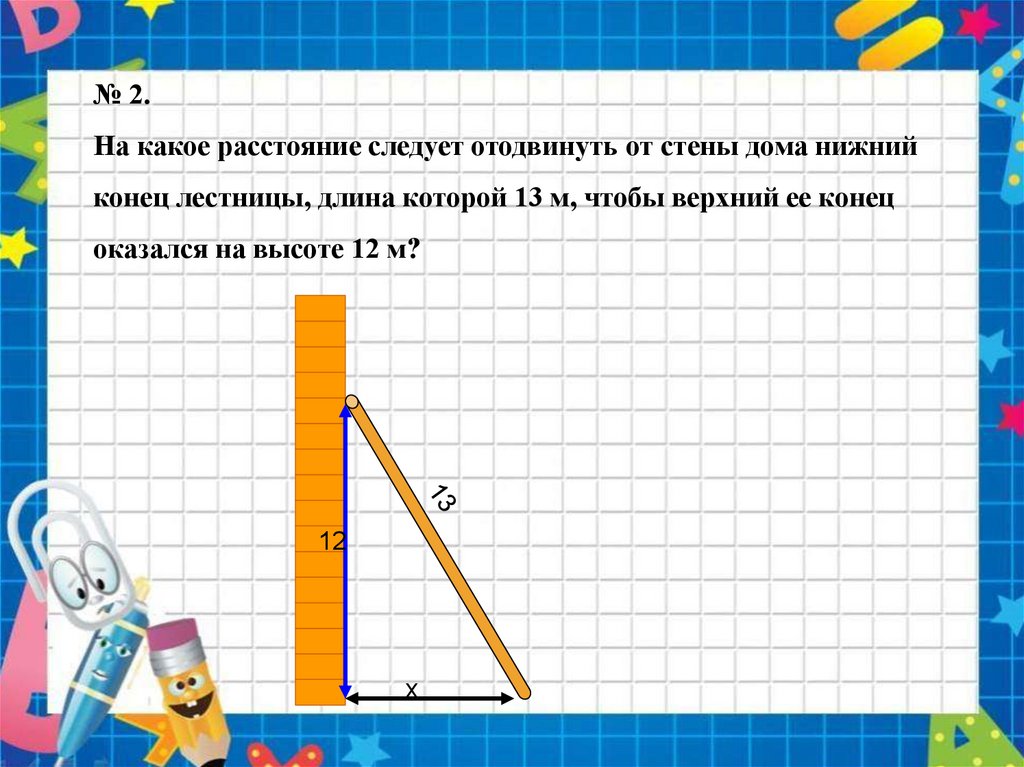
№ 2.
На какое расстояние следует отодвинуть от стены дома нижний
конец лестницы, длина которой 13 м, чтобы верхний ее конец
оказался на высоте 12 м?
12
х

16.

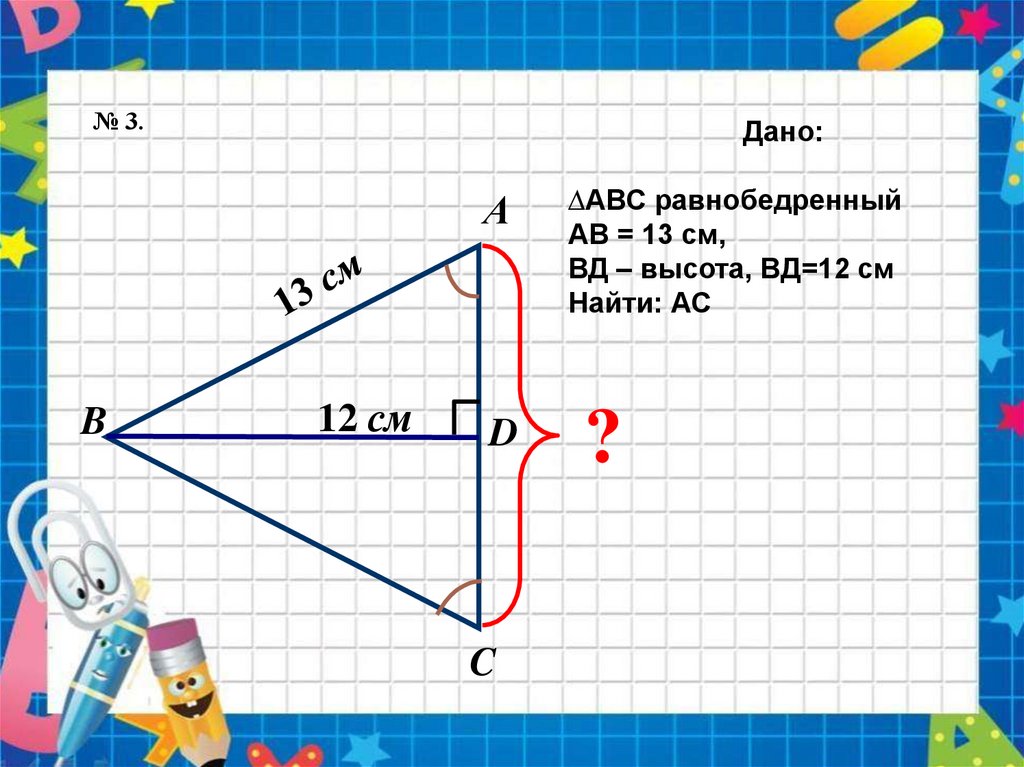
№ 3.
Дано:
А
B
12 см
D
C
∆АВС равнобедренный
АВ = 13 см,
ВД – высота, ВД=12 см
Найти: АС
?

17.

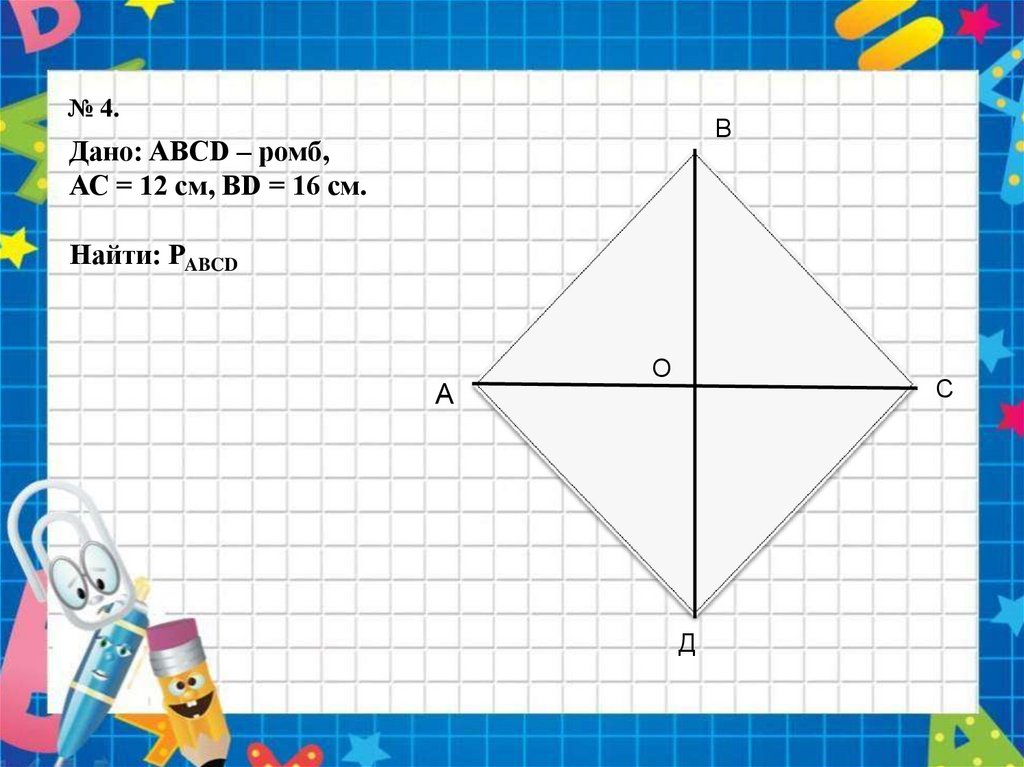
№ 4.
В
Дано: ABCD – ромб,
АС = 12 см, BD = 16 см.
Найти: PABCD
А
О
С
Д

18.

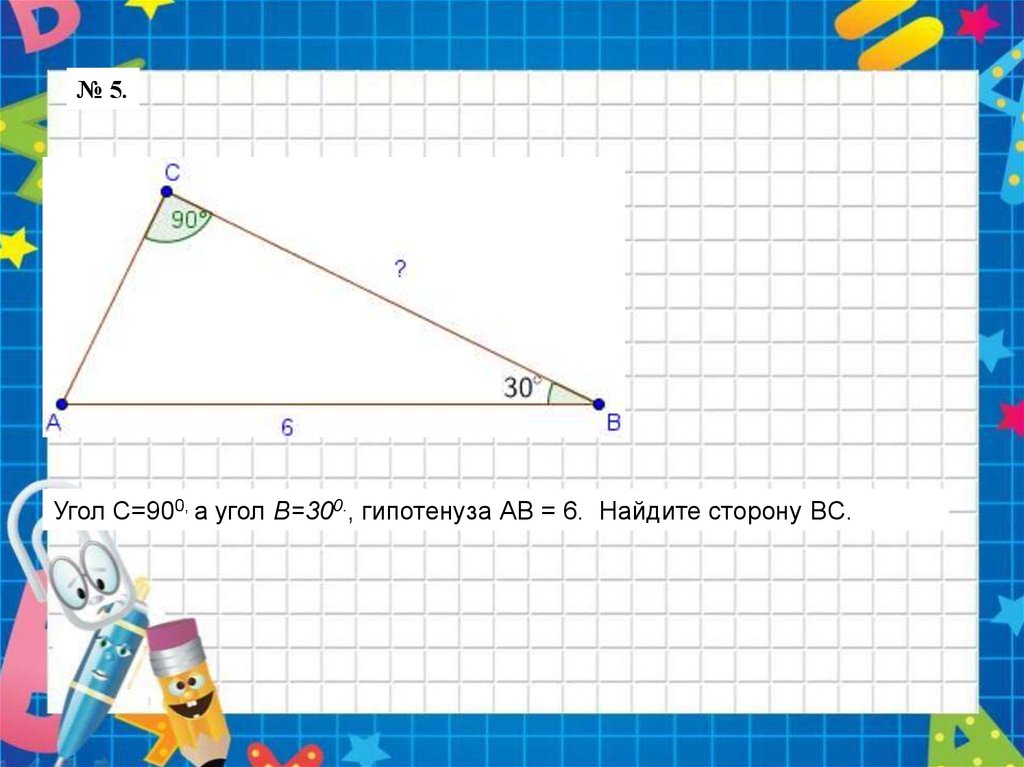
№ 5.
Угол С=900, а угол B=300., гипотенуза АВ = 6. Найдите сторону BC.

19.

IV. Тест
1. Теорему какого учёного мы применяли сегодня на уроке?
а) Демокрита; б) Магницкого; в) Пифагора; г) Ломоносова.
2. Что открыл этот математик
а) теорему; б) рукопись; в) древний храм; г) задачу.
3. Как называется большая сторона в прямоугольном треугольнике?
а) медиана; б) катет; в) биссектриса; г) гипотенуза.
4. Почему теорему назвали «теоремой невесты»
а)потому, что она была написана для невесты;
б) потому, что она была написана невестой;
в) потому, что чертеж похож на «бабочку», а «бабочка»
переводится как «нимфа» или» невеста»;
г) потому, что это загадочная теорема.

20.

5. Почему теорему назвали «мостиком ослов»
а) она применялась для дрессировки осликов;
б) только умный и упрямый мог преодолеть этот мостик и
доказать эту теорему;
в) написали ее «ослики»;
г) очень сложное доказательство теоремы.
6. В теореме Пифагора квадрат гипотенузы равен
а) сумме длин сторон треугольника;
б) сумме квадратов катетов;
в) площади треугольника;
г) площади квадрата.
7. Чему равны стороны египетского треугольника?
а) 1, 2, 3; б) 3,4,5; в) 2,3,4; г) 6, 7, 8.

21.

8. Домашнее задание:
№ 491, № 492, № 493.

22.

8. ИТОГ УРОКА
Теорема Пифагора издавна широко применялась в
разных областях науки, техники и практической
жизни. О ней писали в своих произведениях
римский архитектор и инженер Витрувий, греческий
писатель-моралист Плутарх, математик v века
Прокл и другие.
«Как хорошо, когда благоденствие человека
основано на законах разума».
Будьте благоразумными.