Similar presentations:
Аксиомы стереометрии. Основные фигуры в пространстве
1.
Государственное бюджетное общеобразовательноеучреждение школа №543
Московского района Санкт-Петербурга
Аксиомы стереометрии
Учитель математики
высшей категории
Чагина Юлия Анатольевна
2020
2.
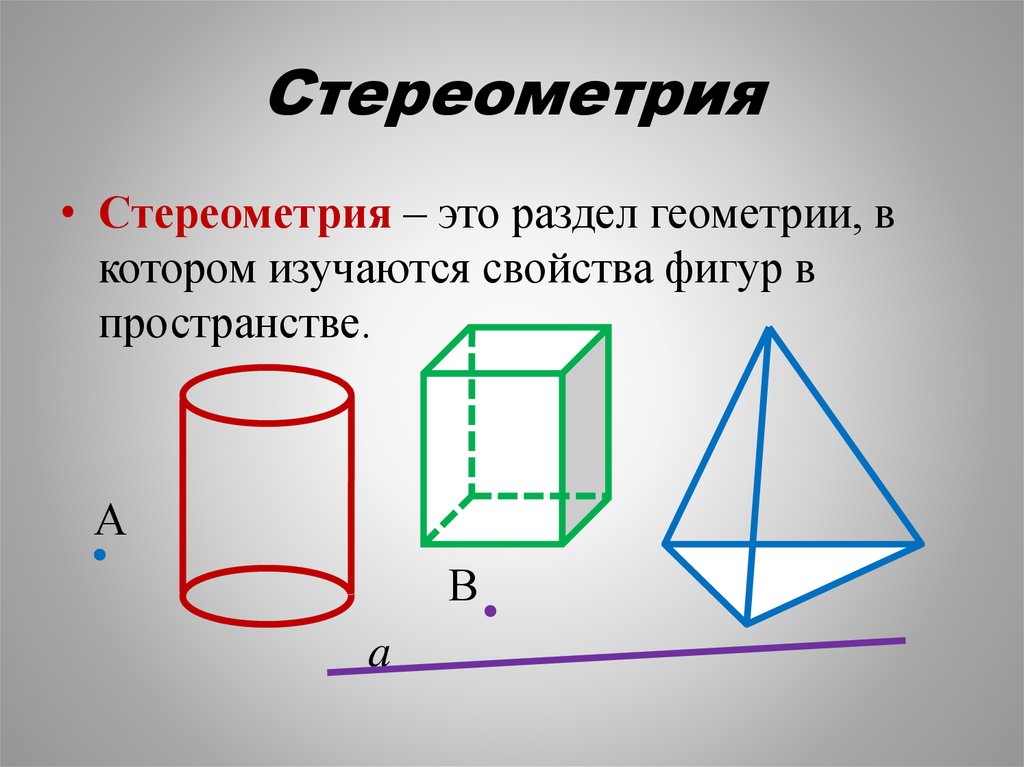
Стереометрия• Стереометрия – это раздел геометрии, в
котором изучаются свойства фигур в
пространстве.
А
В
a
3.
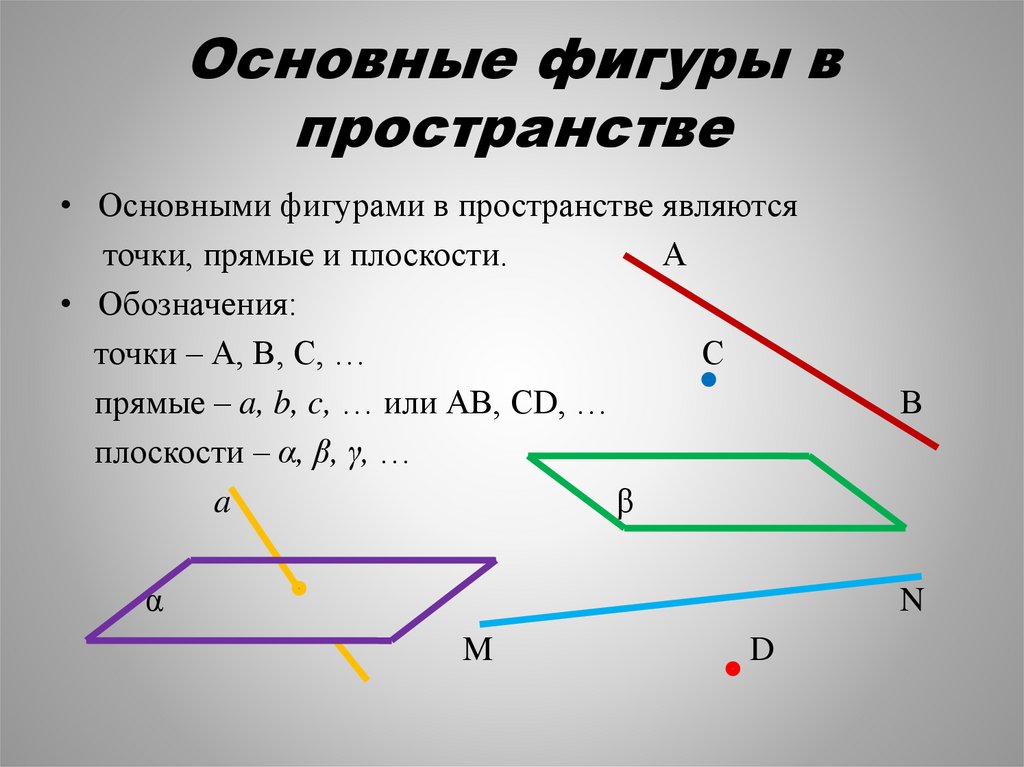
Основные фигуры впространстве
• Основными фигурами в пространстве являются
точки, прямые и плоскости.
А
• Обозначения:
точки – А, В, С, …
С
прямые – a, b, c, … или АВ, СD, …
плоскости – α, β, γ, …
a
β
α
В
N
M
D
4.
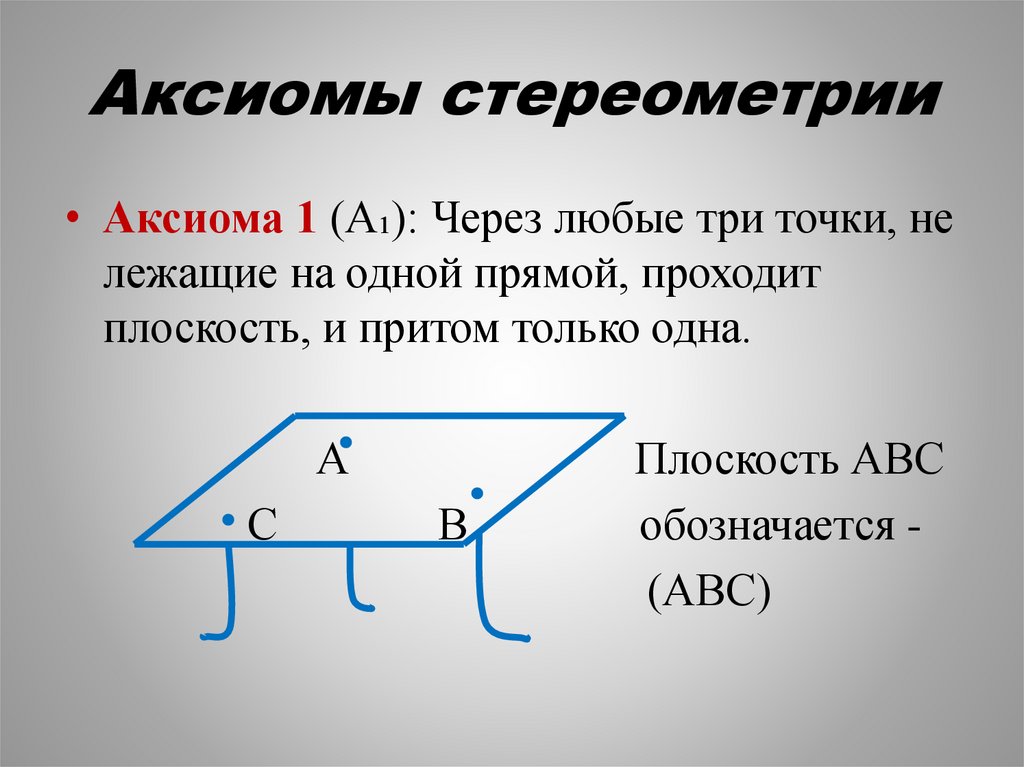
Аксиомы стереометрии• Аксиома 1 (А₁): Через любые три точки, не
лежащие на одной прямой, проходит
плоскость, и притом только одна.
А
С
В
Плоскость АВС
обозначается (АВС)
5.
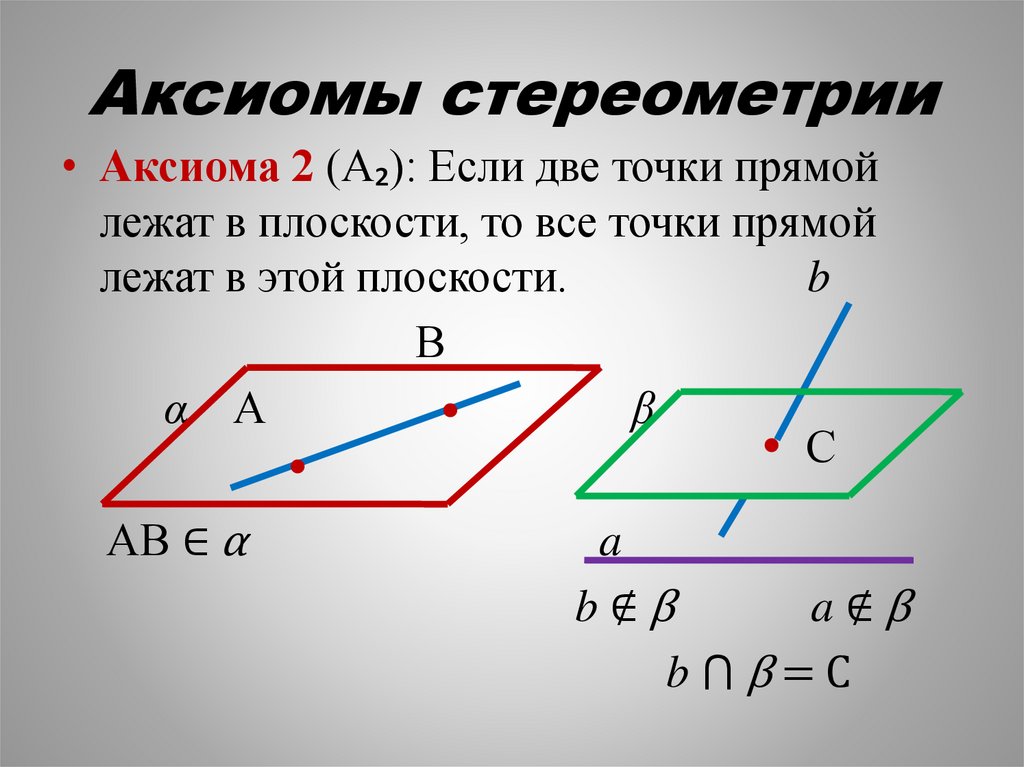
Аксиомы стереометрии• Аксиома 2 (А₂): Если две точки прямой
лежат в плоскости, то все точки прямой
лежат в этой плоскости.
b
В
α А
β
С
АВ ∈ α
a
b∉β
a∉β
b⋂β=C
6.
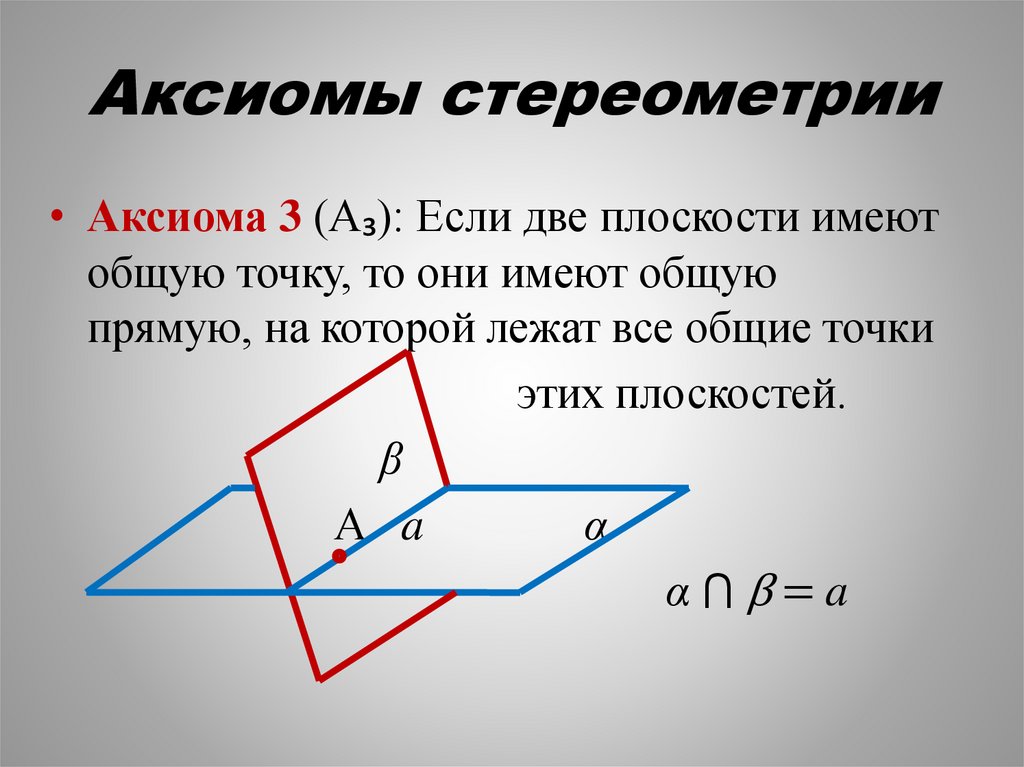
Аксиомы стереометрии• Аксиома 3 (А₃): Если две плоскости имеют
общую точку, то они имеют общую
прямую, на которой лежат все общие точки
этих плоскостей.
β
А a
α
α⋂β=a
7.
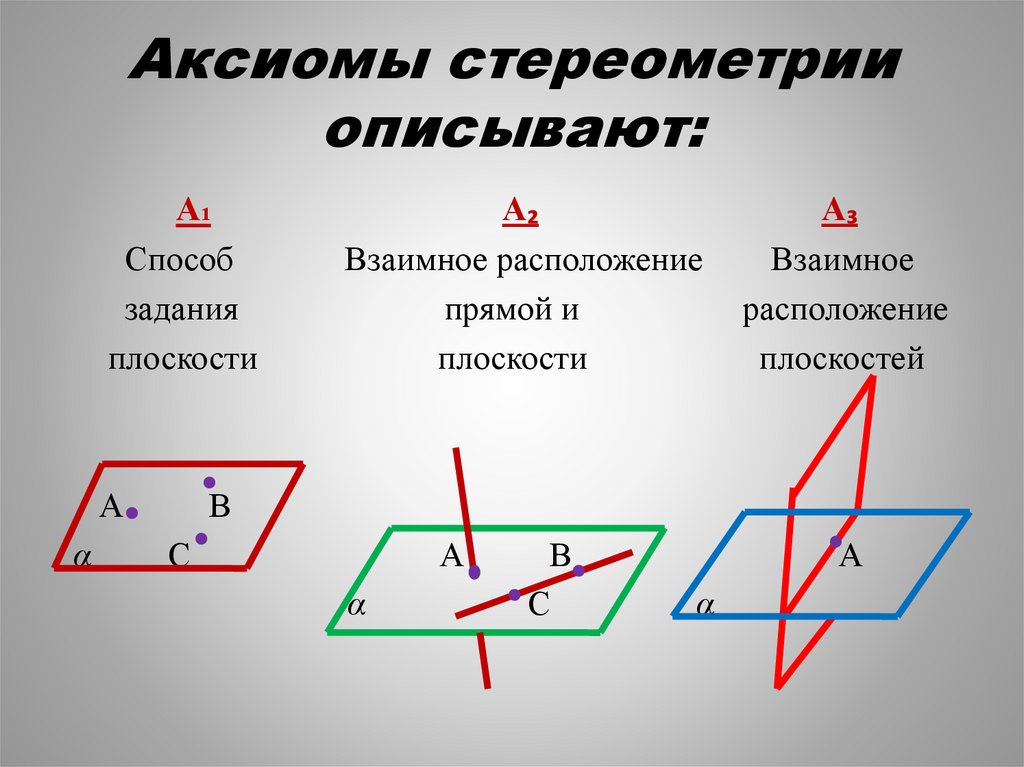
Аксиомы стереометрииописывают:
А₁
Способ
задания
плоскости
А
α
А₂
Взаимное расположение
прямой и
плоскости
А₃
Взаимное
расположение
плоскостей
В
С
А
α
В
С
А
α
8.
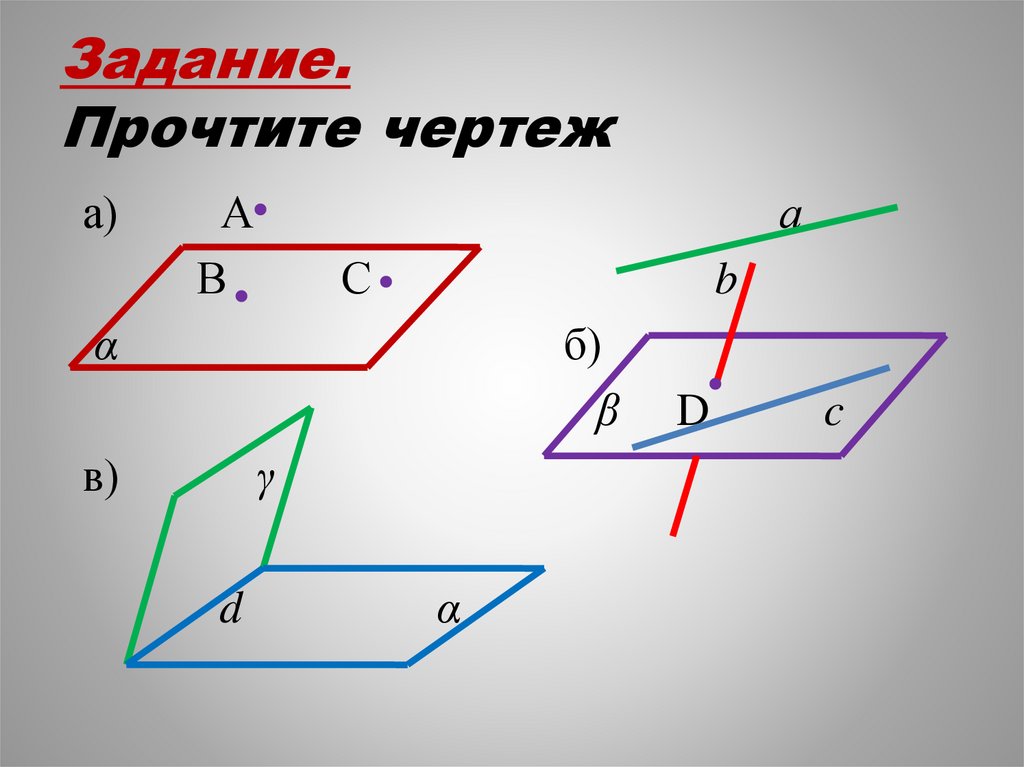
Задание.Прочтите чертеж
а)
А
В
а
С
b
α
б)
β
в)
γ
d
α
D
c
9.
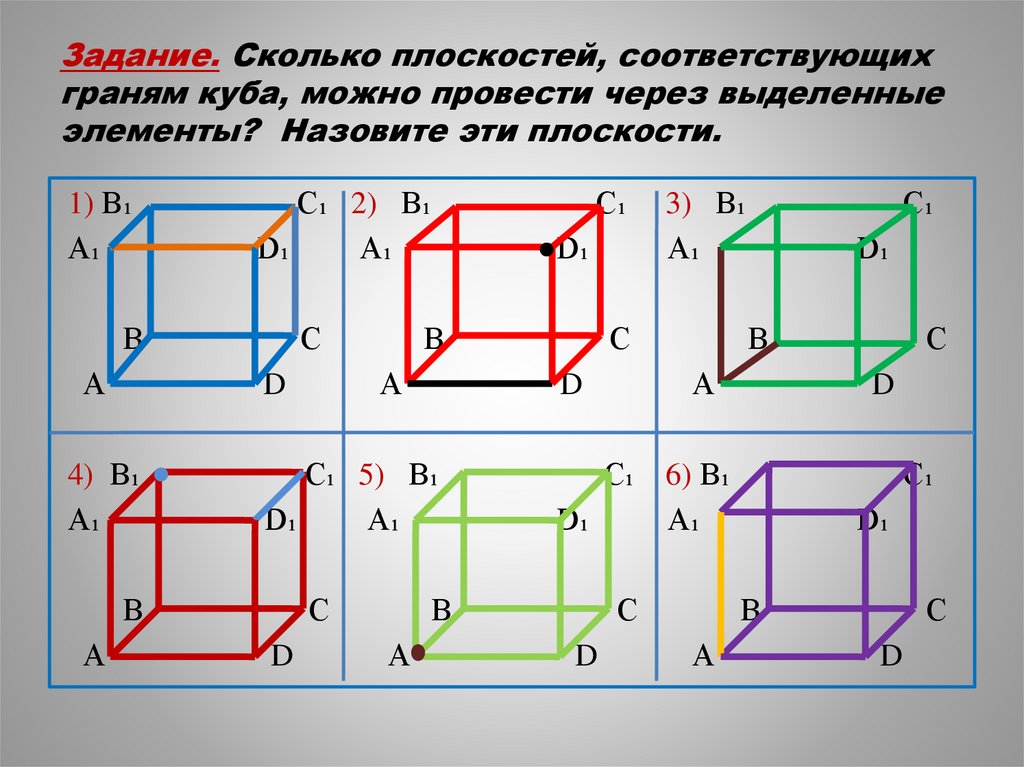
Задание. Сколько плоскостей, соответствующихграням куба, можно провести через выделенные
элементы? Назовите эти плоскости.
1) В₁
А₁
С₁ 2) В₁
D₁
А₁
В
А
С
В
С
D
D₁
D₁
В
С
D
6) В₁
А₁
С
D
С₁
А
С₁
В
А
3) В₁
А₁
С
D
С₁ 5) В₁
D₁
А₁
В
А
D₁
А
D
4) В₁
А₁
С₁
С₁
D₁
В
А
С
D
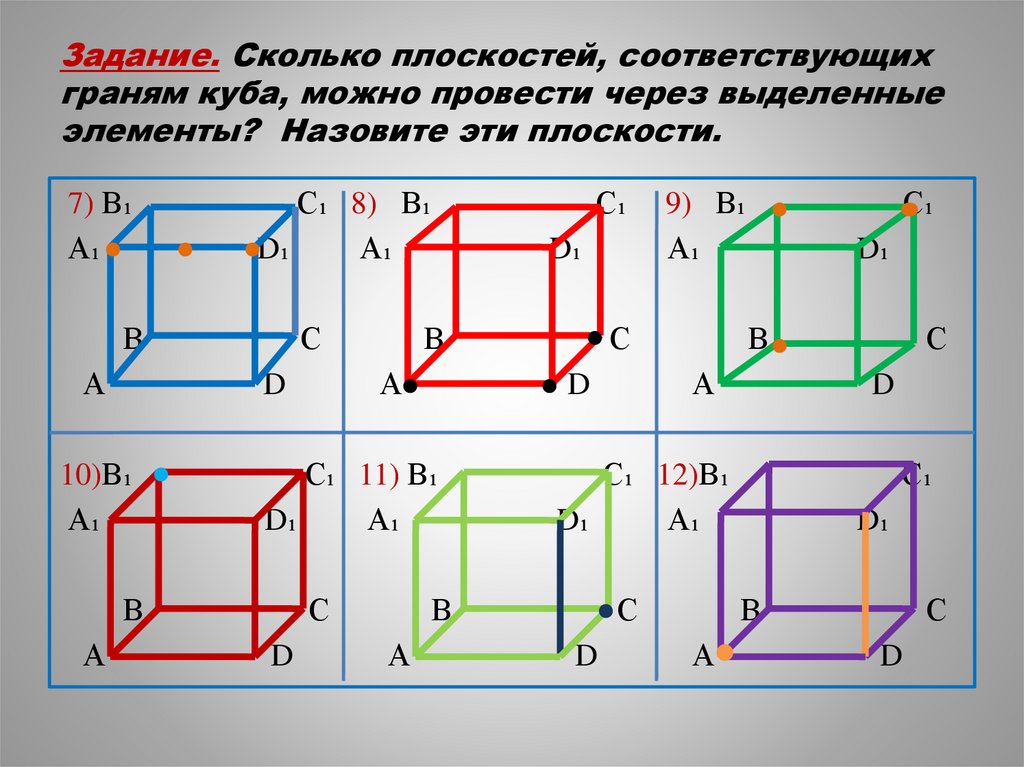
10.
Задание. Сколько плоскостей, соответствующихграням куба, можно провести через выделенные
элементы? Назовите эти плоскости.
7) В₁
А₁
С₁ 8) В₁
D₁
А₁
В
А
С
В
С
D
С₁
D₁
В
А
С
D
С
D
С₁ 12)В₁
D₁
А₁
В
А
9) В₁
А₁
С
D
С₁ 11) В₁
D₁
А₁
В
А
D₁
А
D
10)В₁
А₁
С₁
С₁
D₁
В
А
С
D
11.
ЗадачиРешите устно, постройте чертеж
• 1) Точки А, В и С лежат на одной прямой,
точка D не лежит на ней. Через каждые три
точки проведена плоскость. Тогда число
различных плоскостей равно…
• 2) Плоскости α и β пересекаются по прямой
m. Точка А лежит в плоскости α, точка В –
в плоскости β. Тогда прямая АВ лежит в
плоскости β, если…
12.
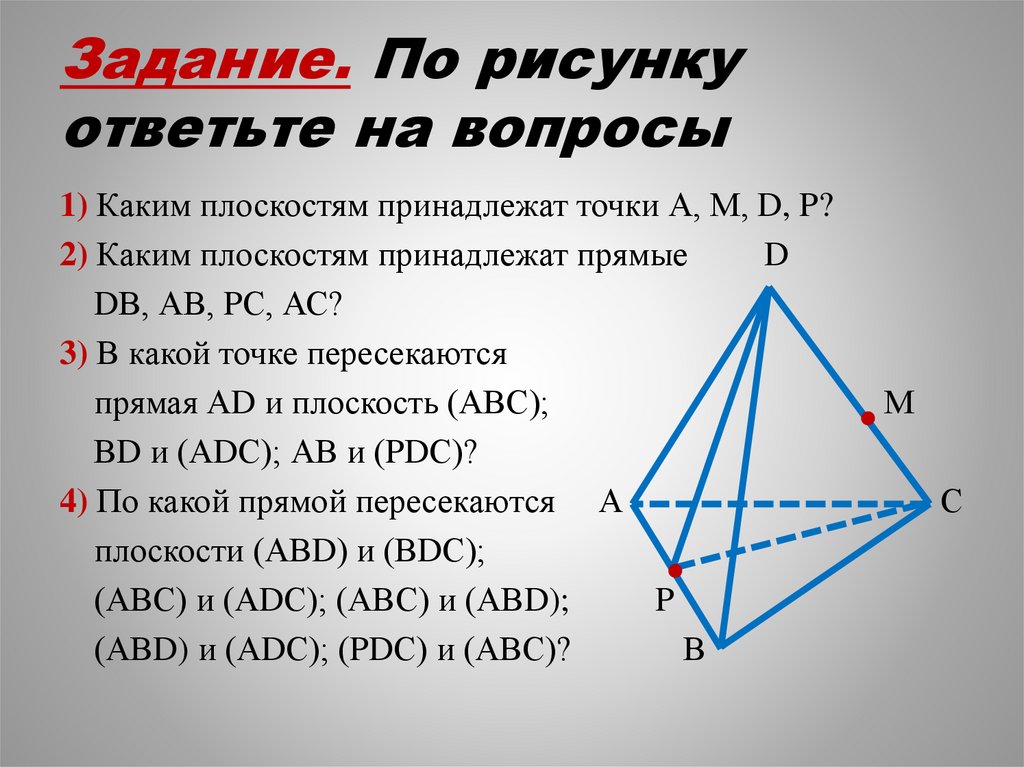
Задание. По рисункуответьте на вопросы
1) Каким плоскостям принадлежат точки А, М, D, P?
2) Каким плоскостям принадлежат прямые
D
DВ, АВ, PС, АС?
3) В какой точке пересекаются
прямая АD и плоскость (АВС);
ВD и (АDС); АВ и (PDС)?
4) По какой прямой пересекаются А
плоскости (АВD) и (ВDС);
(АВС) и (АDС); (АВС) и (АВD);
P
(АВD) и (АDС); (PDС) и (АВС)?
В
М
С
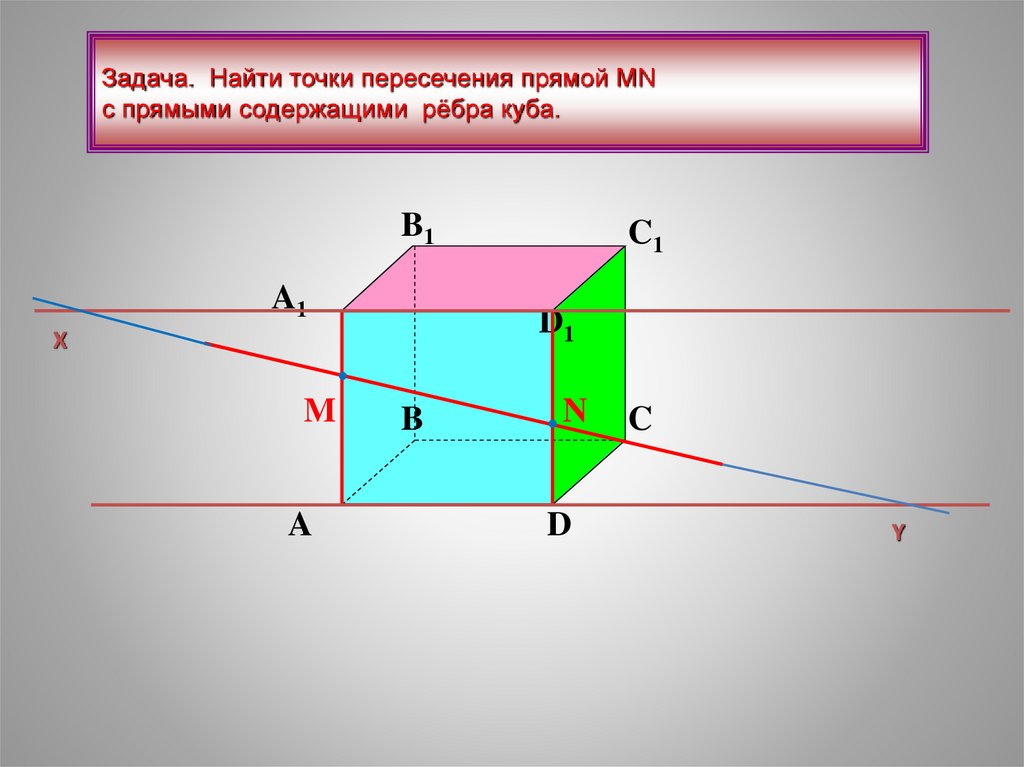
13.
Задача. Найти точки пересечения прямой МNс прямыми содержащими рёбра куба.
B1
A1
C1
D1
Х
M
A
B
•N
D
C
Y
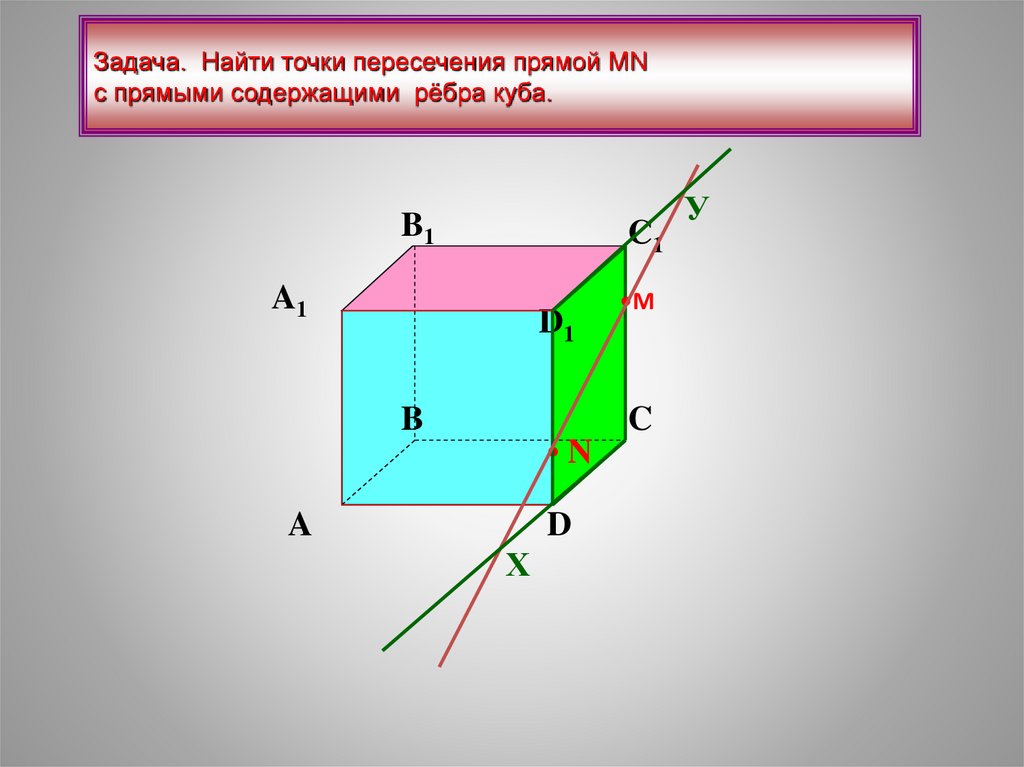
14.
Задача. Найти точки пересечения прямой МNс прямыми содержащими рёбра куба.
B1
C1
A1
D1
B
•N
A
D
Х
•M
C
У
15.
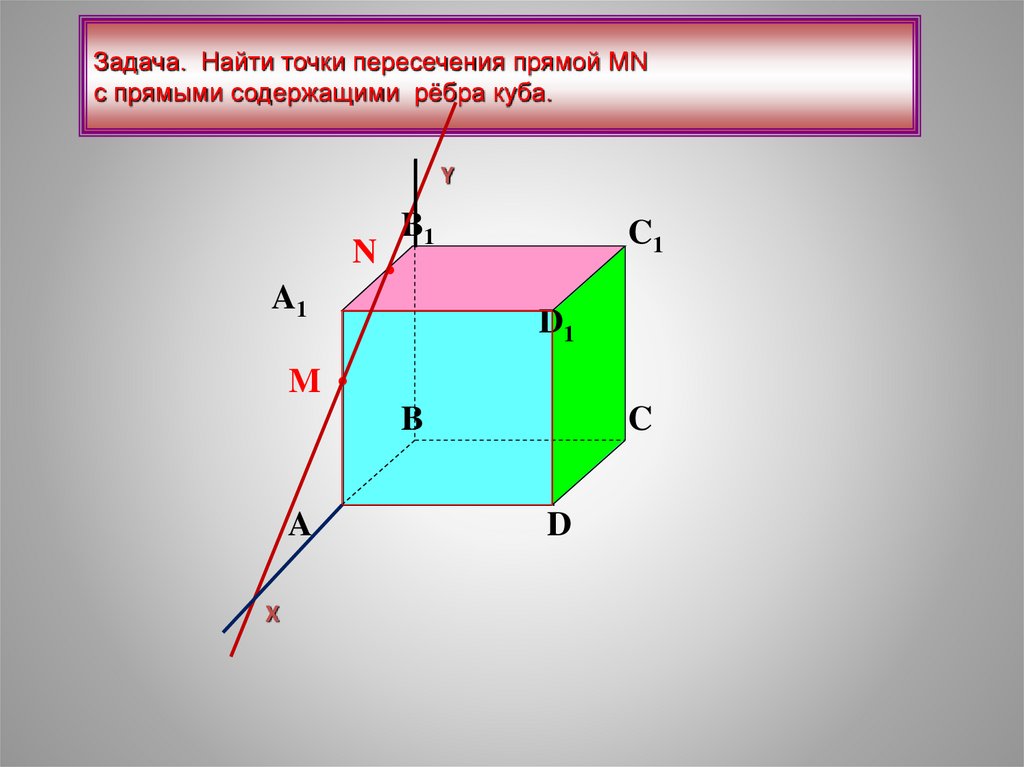
Задача. Найти точки пересечения прямой МNс прямыми содержащими рёбра куба.
Y
N
A1
B1
C1
D1
M
B
A
Х
C
D
16.
Задача. Найти точки пересечения прямой МNс прямыми содержащими рёбра тетраэдра.
D
•М
А
N
В
С
X



 mathematics
mathematics








