Арифметический корень натуральной степени и его свойства

1.

27.11.2023

2.

3.

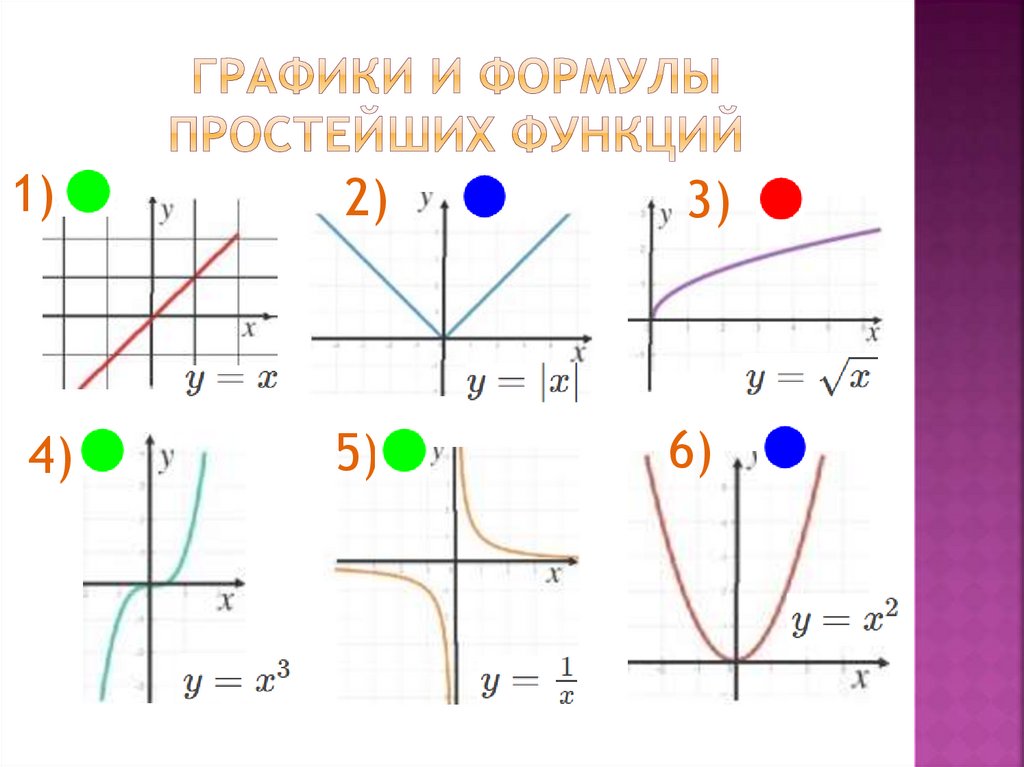
1)
2)
3)
4)
5)
6)

4.

5.

Анализ ошибок
контрольной работы № 2.
Презентация 2.

6.

Арифметический корень
натуральной степени
и его свойства

7.

Площадь квадрата S=16 м².
Обозначим сторону квадрата а, м.
Тогда, а² = 16.
a=4 и а= –4.
Проверим решение:
4² = 16;
(–4)² = 16.
Ответ: длина стороны квадрата равна 4 м.
Определение.
Квадратным корнем из числа a называют такое число, квадрат
которого будет равен a.
Определение.
Арифметическим квадратным корнем из числа
неотрицательное число, квадрат которого равен а.
Обозначение:
.
а
называют

8.

Определение.
Кубический корень из а — это такое число, которое при
возведении в третью степень дает число а.
Обозначение:
.
Примеры:
На основании определений квадратного и кубического корней,
можно сформулировать определения корня n-ой степени и
арифметического корня n-ой степени.
Определение.
Корнем n-ой степени из числа a называют такое число, n-ая
степень которого будет равна a.
Обозначение:
Примеры:
– корень n-й степени, где
n – степень арифметического корня;
a – подкоренное выражение.
т.к.
значит,

9.

На основании этих примеров, можно сделать
вывод:
при условии, что n –нечетное число.
Свойства арифметического корня
натуральной степени:
Если а ≥ 0, b ≥ 0 и m , n – натуральные числа, причем m ≥ 2, n ≥ 2, то
справедливо следующее:

10.

11.

Выберите верные утверждения:

12.

Выделите самое маленькое число: