Similar presentations:
Математическое моделирование
1.
Умные словаОбъект
То, на что направлена человеческая
деятельность
лат. Objectum ‒ предмет
Максимова Оксана Геннадьевна
2.
Умные словаМодель
Объект-заместитель объекта-оригинала
(прототипа), служащий для изучения
некоторых свойств оригинала
лат. modulus ‒ мера
Максимова Оксана Геннадьевна
3.
Умные мыслиНаилучшей моделью
кота является другой
кот, а ещё лучше ̶ тот
самый кот.
Норберт Винер
Максимова Оксана Геннадьевна
4.
МоделированиеИзучение объекта путём построения и исследования
его модели, которое состоит в замене эксперимента с
оригиналом экспериментом на модели,
осуществляемое с определённой целью
5.
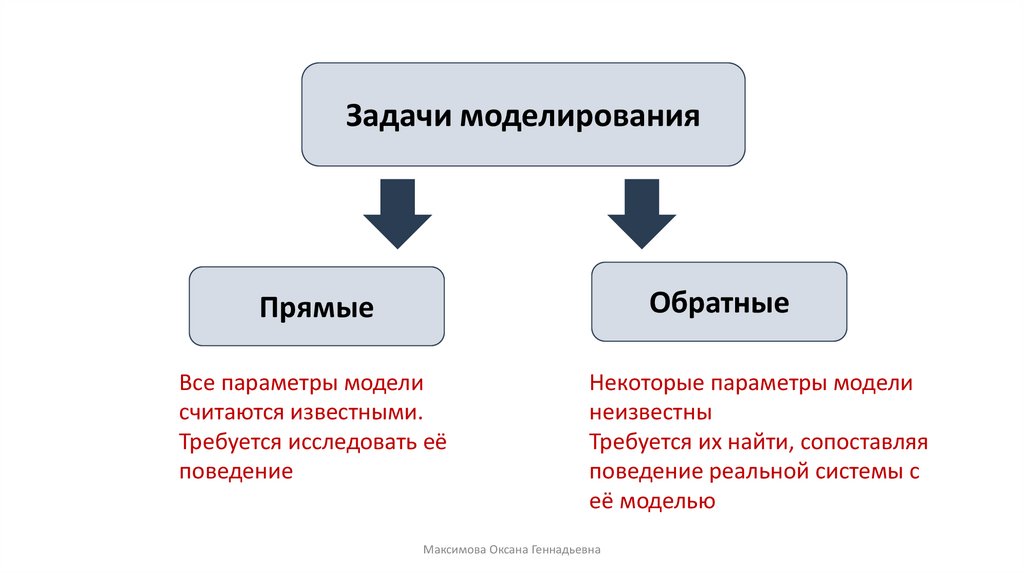
Задачи моделированияОбратные
Прямые
Все параметры модели
считаются известными.
Требуется исследовать её
поведение
Некоторые параметры модели
неизвестны
Требуется их найти, сопоставляя
поведение реальной системы с
её моделью
Максимова Оксана Геннадьевна
6.
Умные словаМатематическая модель
Описание объекта моделирования,
выраженное через математические объекты
An equation representing an idea
Уравнение, выражающее идею
Максимова Оксана Геннадьевна
7.
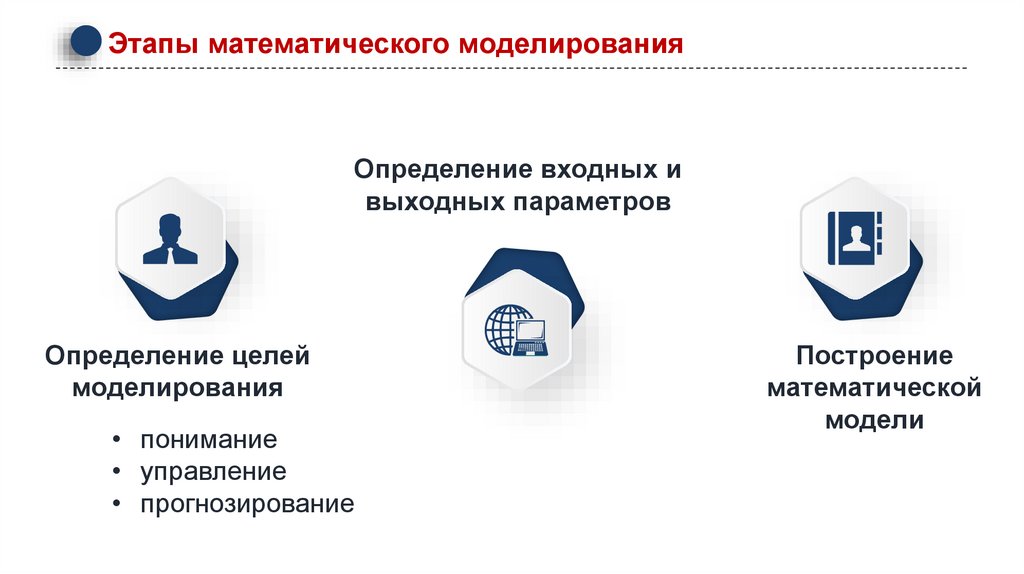
Этапы математического моделированияОпределение входных и
выходных параметров
Определение целей
моделирования
• понимание
• управление
• прогнозирование
Построение
математической
модели
8.
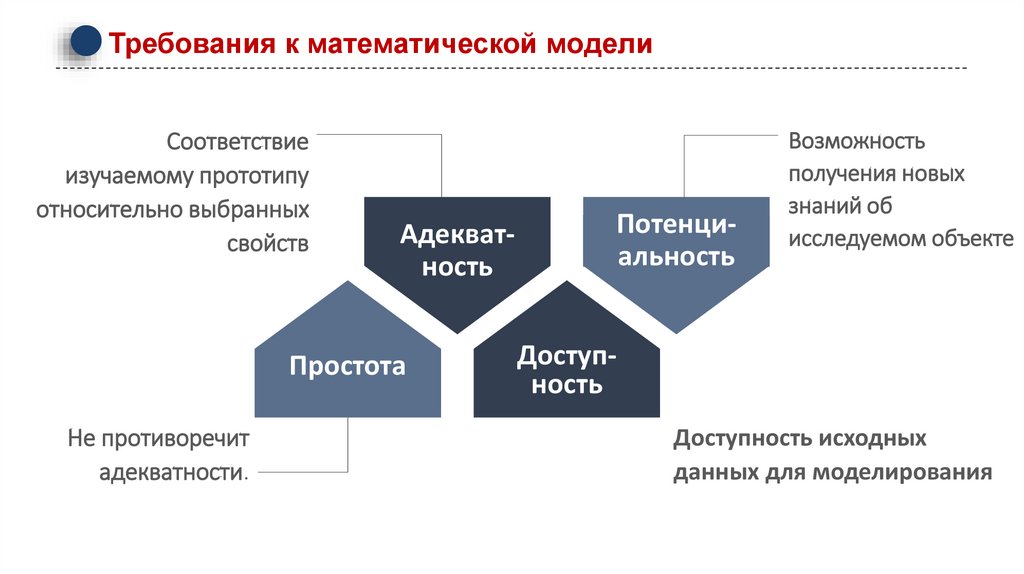
Требования к математической моделиСоответствие
изучаемому прототипу
относительно выбранных
свойств
Адекватность
Простота
Не противоречит
адекватности.
Потенциальность
Возможность
получения новых
знаний об
исследуемом объекте
Доступность
Доступность исходных
данных для моделирования
9.
Классификацияматематических моделей
Математическое моделирование в
теплоэнергетике
10.
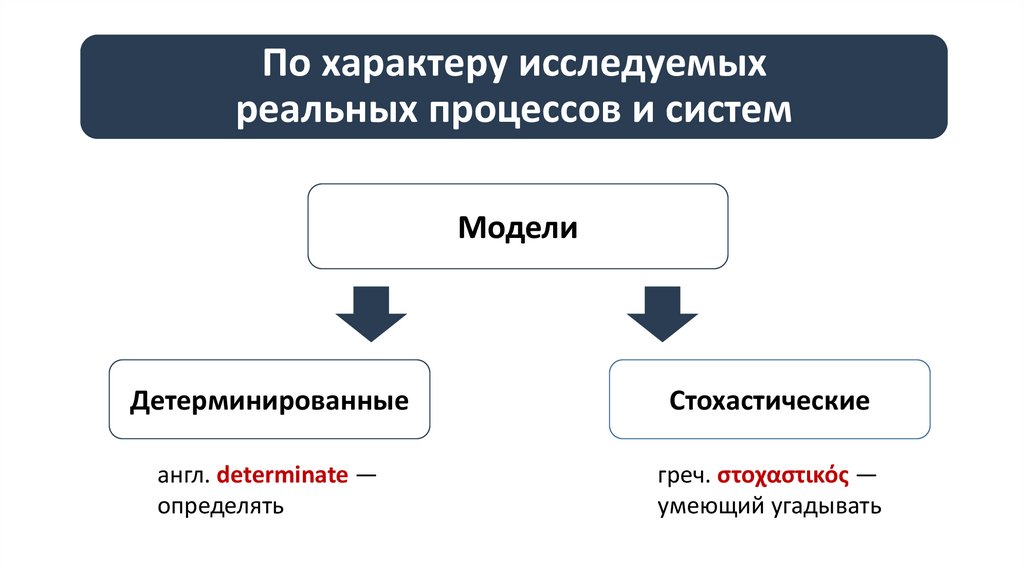
По характеру исследуемыхреальных процессов и систем
Модели
Детерминированные
Стохастические
англ. determinate —
определять
греч. στοχαστικός —
умеющий угадывать
11.
Детерминированныемодели
Стохастические
модели
• Отсутствие случайных
воздействий
• Элементы модели достаточно
точно установлены
• Поведение системы можно точно
определить
• Используются алгебраические
уравнения, интегральные
уравнения, матричная алгебра
• Случайный характер
процессов в исследуемых
объектах и системах
• Описываются методами
теории вероятностей и
математической статистики
12.
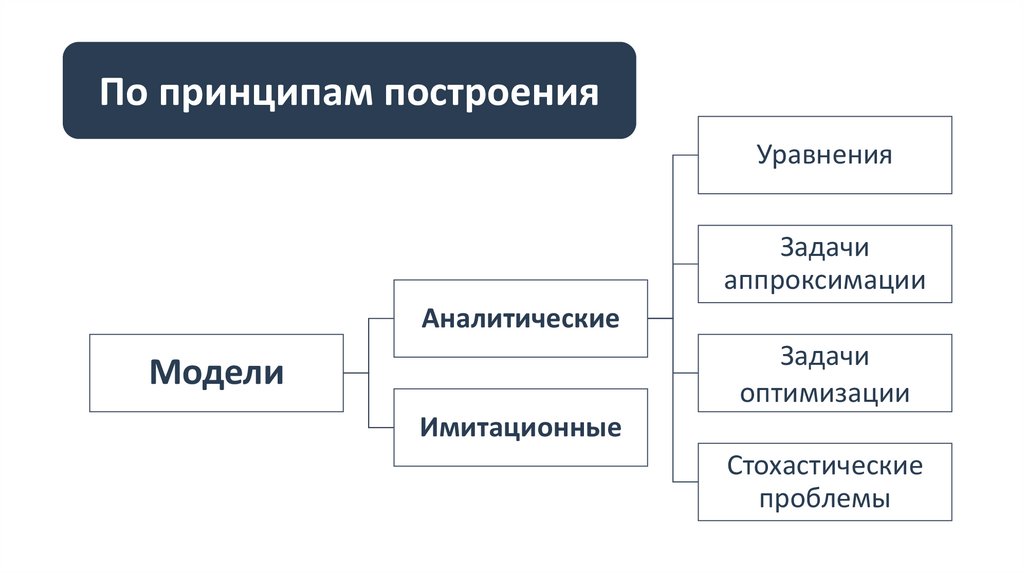
По принципам построенияУравнения
Задачи
аппроксимации
Аналитические
Задачи
оптимизации
Модели
Имитационные
Стохастические
проблемы
13.
Аналитическиемодели
Имитационные
модели
• Записываются в виде
функциональных зависимостей
• По мере усложнения объекта
моделирования построение
аналитической модели
превращается в трудноразрешимую
проблему
• Описываются набором алгоритмов,
имитирующих реальные явления,
составляющие систему, с
сохранением логической структуры
и временной последовательности
• Позволяют по исходным данным
получить сведения о состояниях
системы в определённые моменты
времени
14.
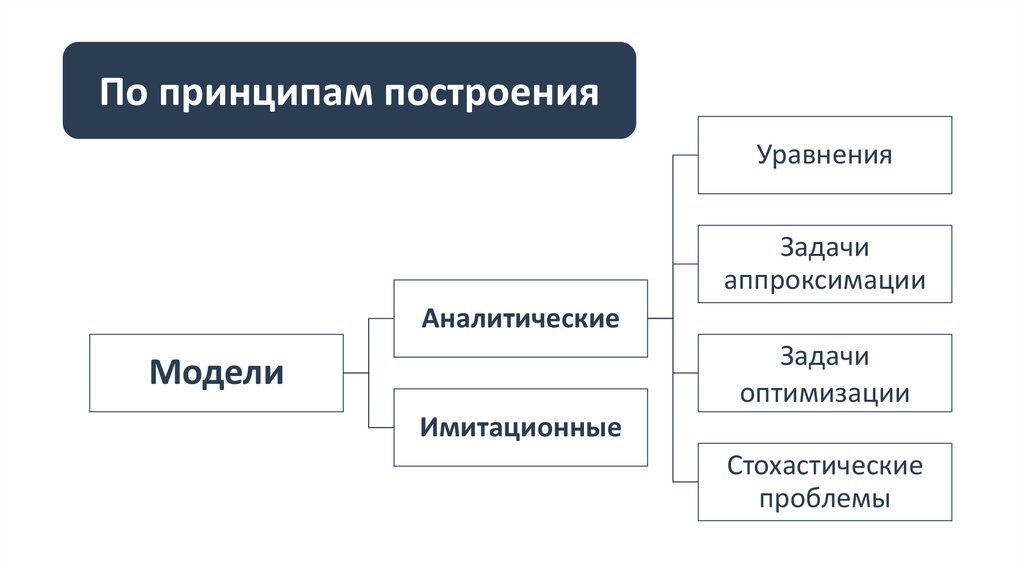
По принципам построенияУравнения
Задачи
аппроксимации
Аналитические
Задачи
оптимизации
Модели
Имитационные
Стохастические
проблемы








 mathematics
mathematics








