Общие сведения о математическом моделировании

1.

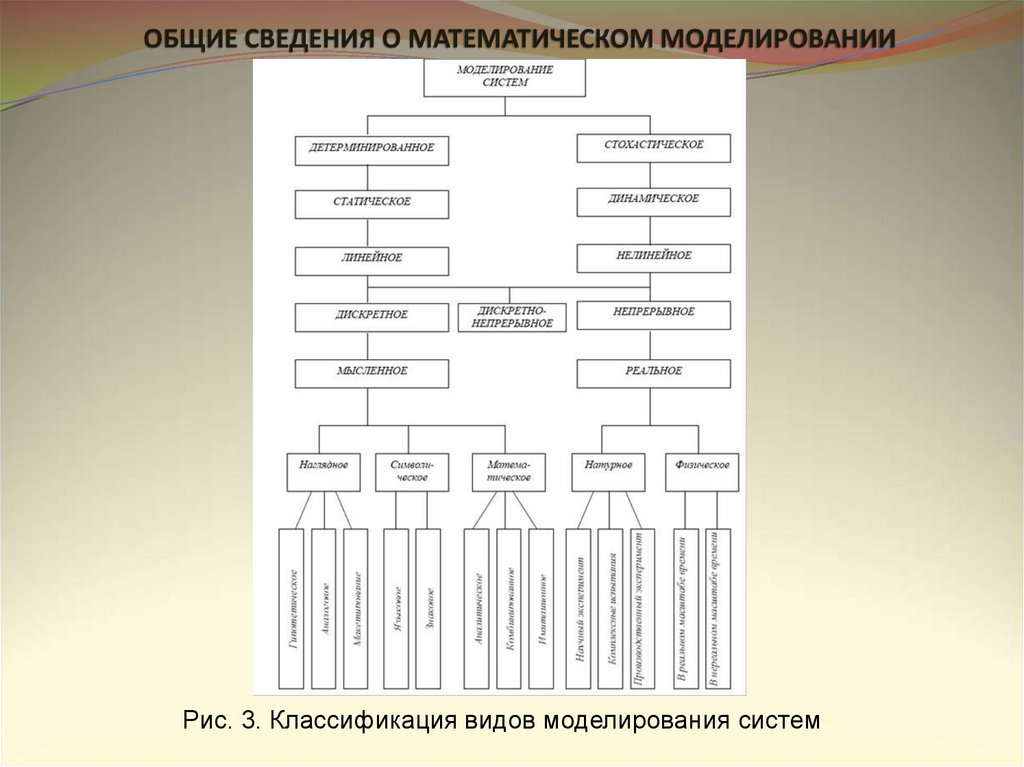
ОБЩИЕ СВЕДЕНИЯ О МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ
Рис. 3. Классификация видов моделирования систем

2.

ОБЩИЕ СВЕДЕНИЯ О МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ
Математические модели
Аналитические
Имитационные
Теоретические
Эмпирические
Теоретические
Линейные
Нелинейные
Нелинейные
Статические
Динамические
Динамические
Детерминированные
Стохастические
Детерминированные
Аналитически
разрешимые
Численно
разрешимые
Численно
разрешимые
Рис. 4. Классификация математических моделей

3.

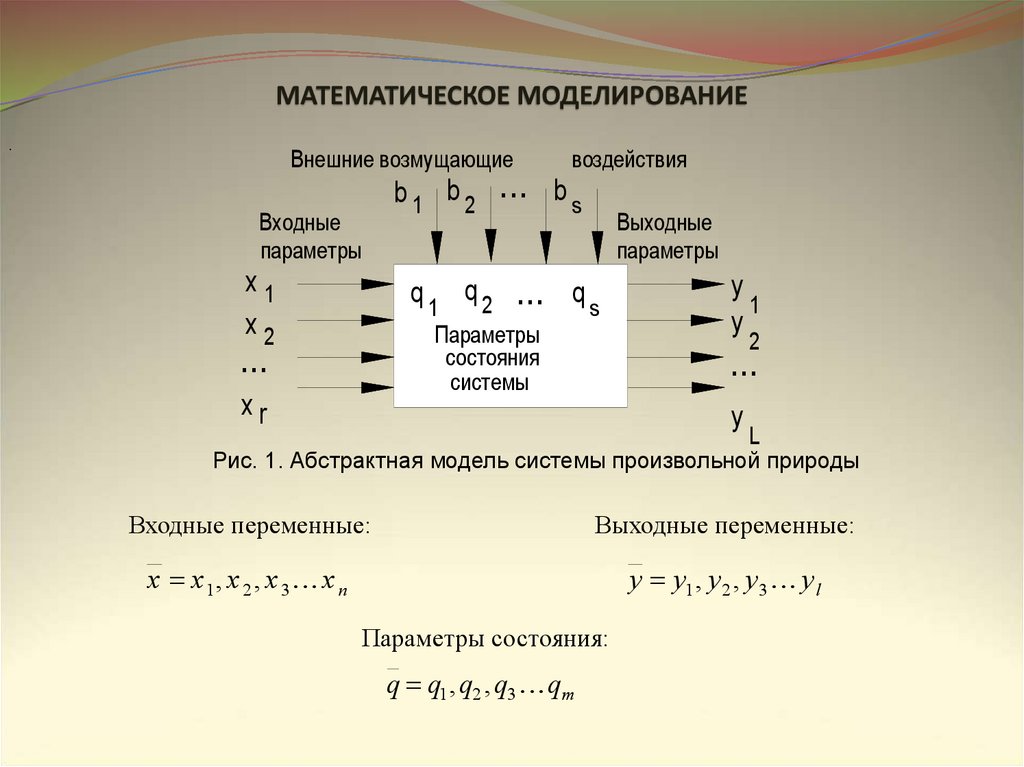
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
.
Внешние возмущающие
Входные
параметры
x1
x2
воздействия
b1 b2
... b s
q1 q2
... q s
Выходные
параметры
Параметры
состояния
системы
...
xr
y
1
y
2
...
y
L
Рис. 1. Абстрактная модель системы произвольной природы
Входные переменные:
Выходные переменные:
x x 1, x 2 , x 3 x n
y y1 , y2 , y3 y l
Параметры состояния:
q q1 , q2 , q3 qm

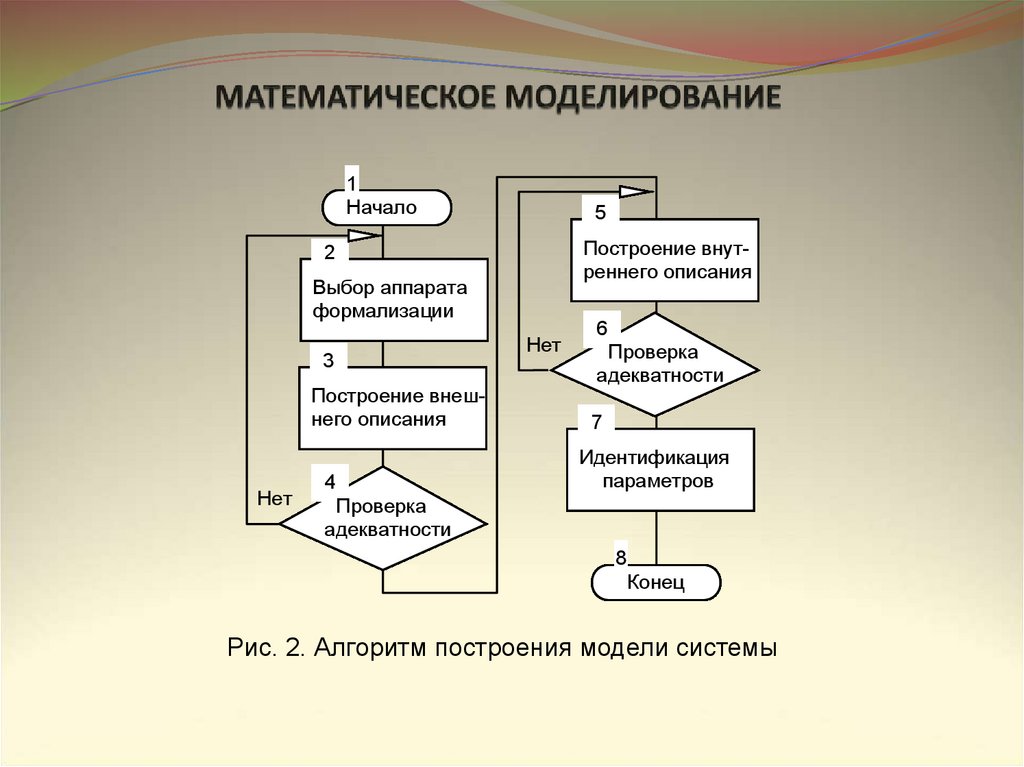
4.

1
Начало
5
Построение внутреннего описания
2
Выбор аппарата
формализации
3
Нет
Нет
6
Проверка
адекватности
Построение внешнего описания
7
4
Идентификация
параметров
Проверка
адекватности
8
Конец
Рис. 2. Алгоритм построения модели системы

5.

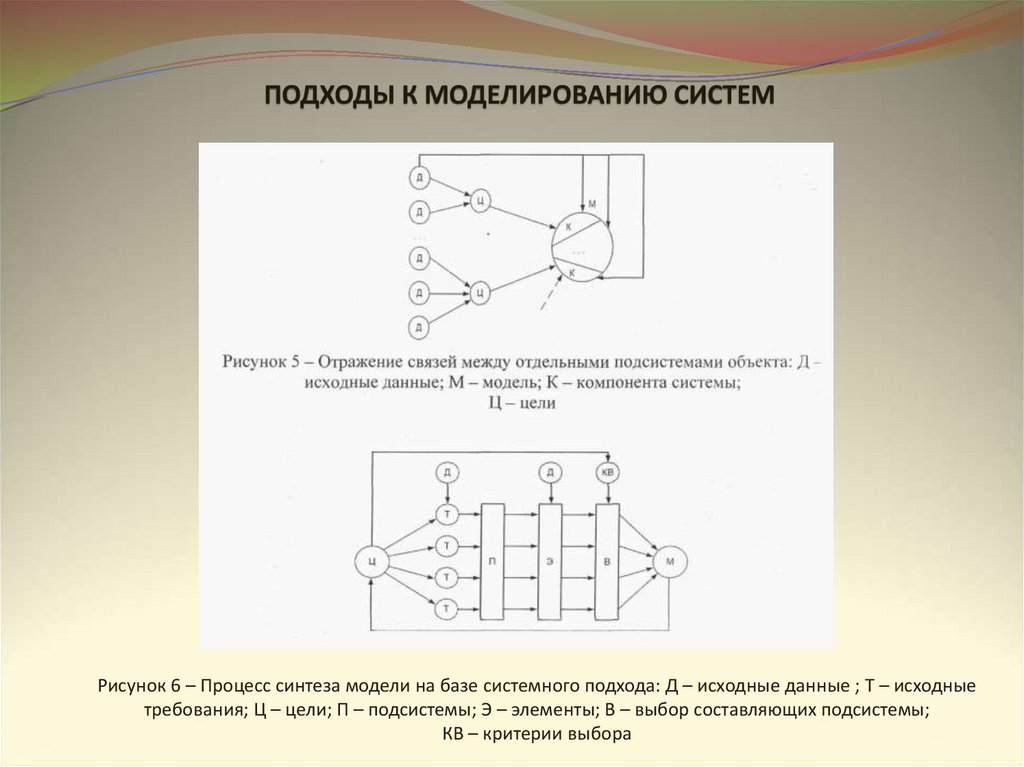
ПОДХОДЫ К МОДЕЛИРОВАНИЮ СИСТЕМ

6.

ПОДХОДЫ К МОДЕЛИРОВАНИЮ СИСТЕМ
Рисунок 6 – Процесс синтеза модели на базе системного подхода: Д – исходные данные ; Т – исходные
требования; Ц – цели; П – подсистемы; Э – элементы; В – выбор составляющих подсистемы;
КВ – критерии выбора

7.

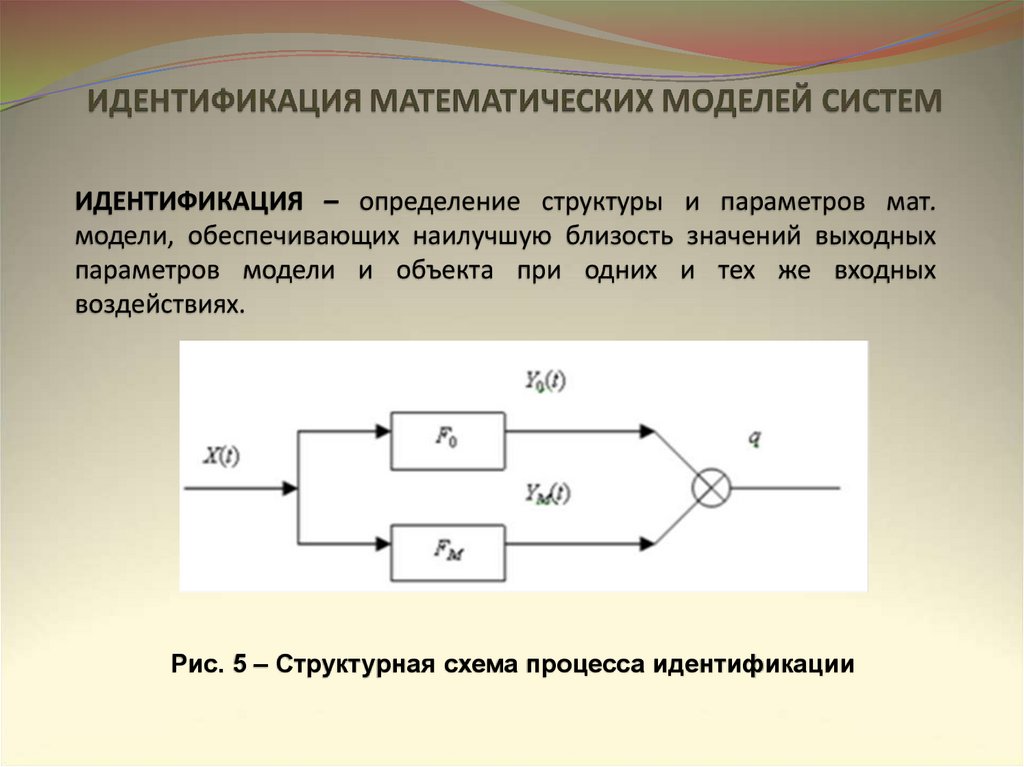
ПОДХОДЫ К МОДЕЛИРОВАНИЮ СИСТЕМ

8.

ИДЕНТИФИКАЦИЯ – определение структуры и параметров мат.
модели, обеспечивающих наилучшую близость значений выходных
параметров модели и объекта при одних и тех же входных
воздействиях.
Рис. 5 – Структурная схема процесса идентификации

9.

Критерий идентичности модели – минимум ее
ошибки q:
Задача идентификации ставится как задача
оптимизации:

10.

11.

12.

13.

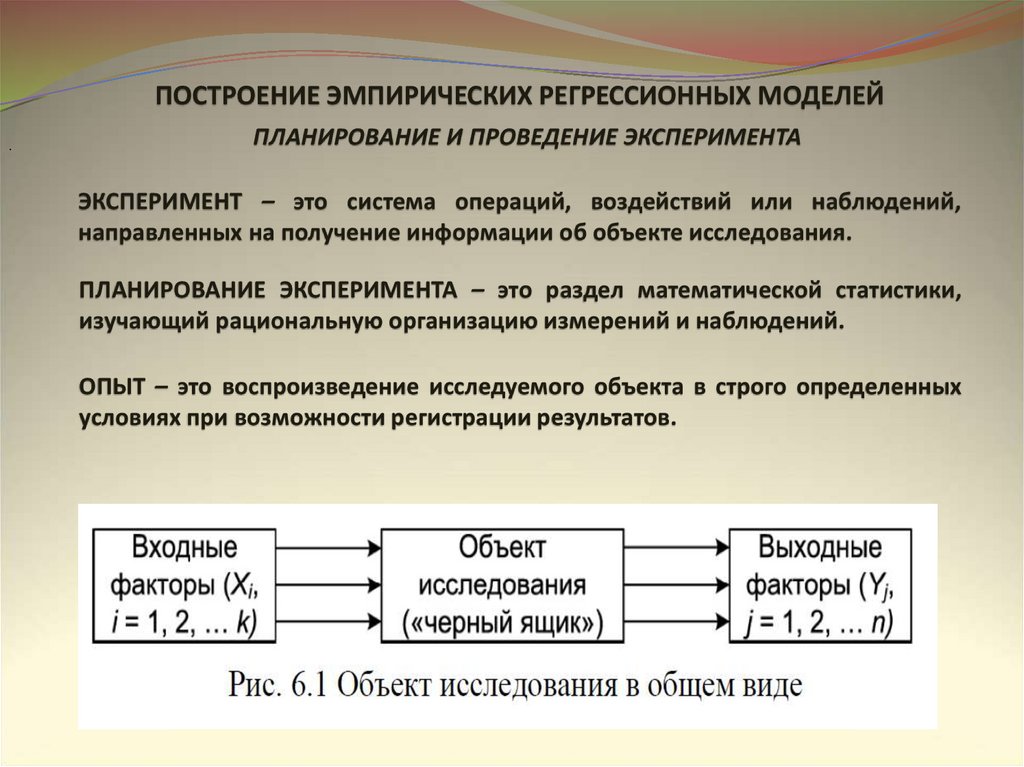
ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
.
ПЛАНИРОВАНИЕ И ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА
ЭКСПЕРИМЕНТ – это система операций, воздействий или наблюдений,
направленных на получение информации об объекте исследования.
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА – это раздел математической статистики,
изучающий рациональную организацию измерений и наблюдений.
ОПЫТ – это воспроизведение исследуемого объекта в строго определенных
условиях при возможности регистрации результатов.

14.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
Количество опытов в эксперименте:
где p э – число уровней каждого входного фактора; k э – число входных факторов,
исследуемых в эксперименте
Если исследуемая зависимость Y j =f (X 1, X 2, … X k) является линейной, то
достаточно реализовать эксперимент, в котором каждый входной фактор
имеет в эксперименте только два уровня, т. е.
Если исследуемая зависимость Y j =f (X 1, X 2, … X k) является нелинейной, то
достаточно реализовать эксперимент, в котором каждый входной фактор
имеет в эксперименте три уровня:

15.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ

16.

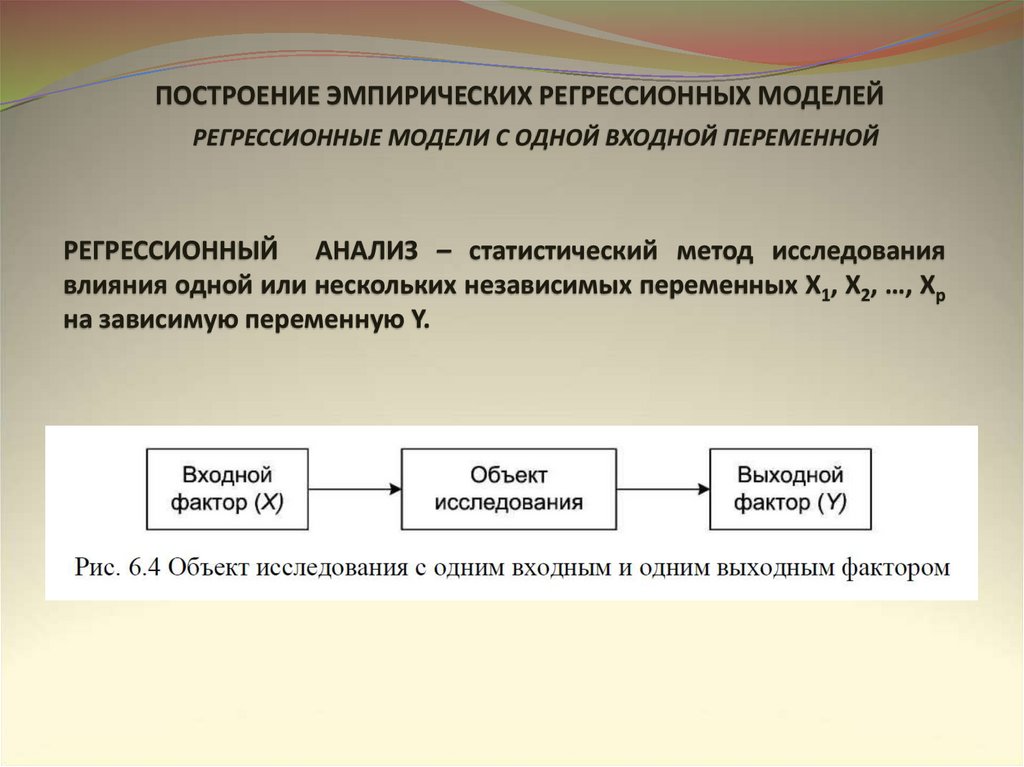
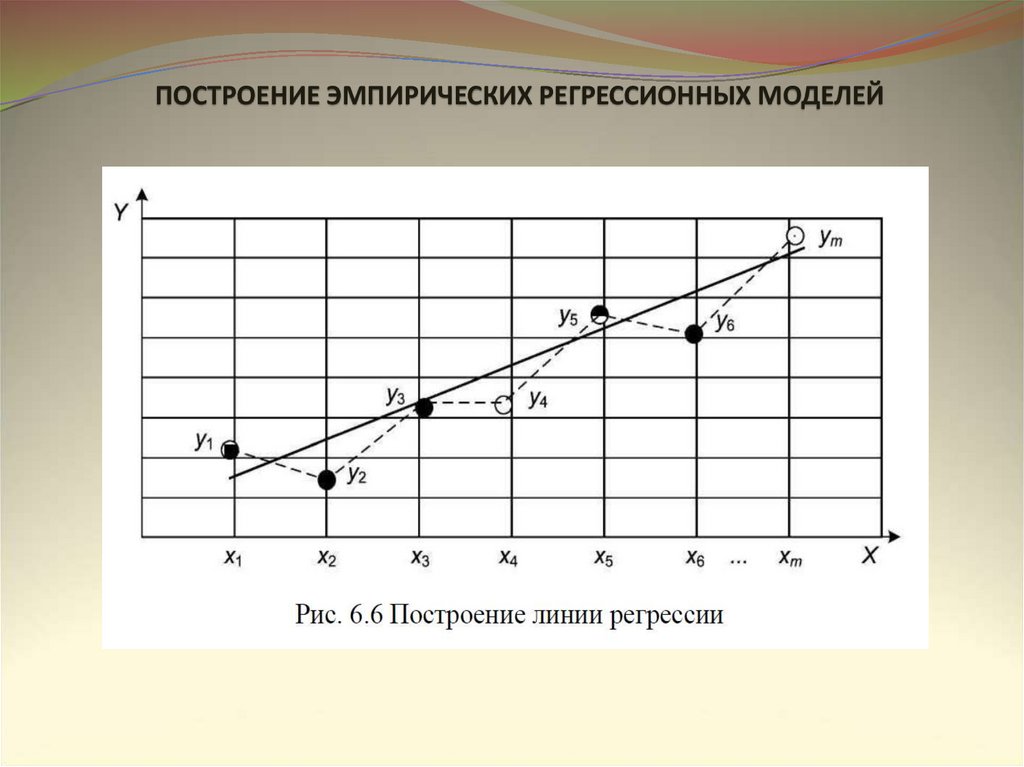
ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ

17.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
РЕГРЕССИОННЫЕ МОДЕЛИ С ОДНОЙ ВХОДНОЙ ПЕРЕМЕННОЙ
РЕГРЕССИОННЫЙ АНАЛИЗ – статистический метод исследования
влияния одной или нескольких независимых переменных Х1, Х2, …, Хр
на зависимую переменную Y.

18.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ

19.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ

20.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
Если имеется неограниченно большое количество
экспериментальных точек, то линейная регрессионная
модель имеет вид:

21.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ

22.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
ОДНОФАКТОРНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ:

23.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
КОЭФФИЦИЕНТ РЕГРЕССИИ:

24.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
Адекватность регрессионных моделей оценивается коэффициентом Фишера:
Точность регрессионных моделей:

25.

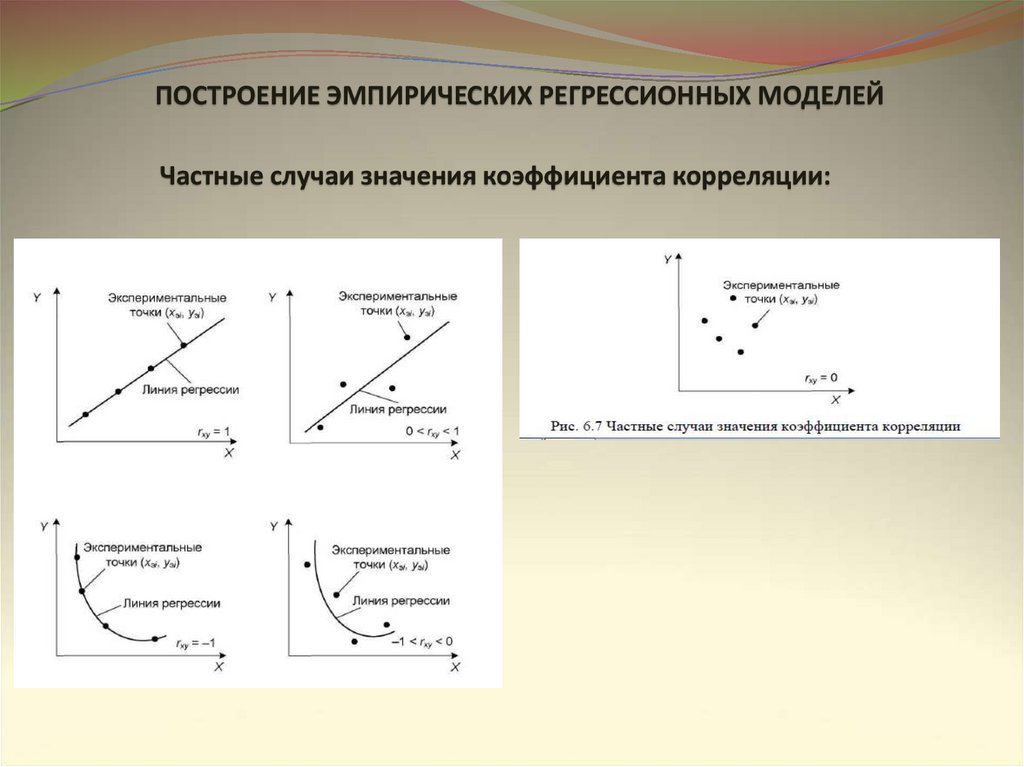
ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
Частные случаи значения коэффициента корреляции:

26.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
РЕГРЕССИОННЫЕ МОДЕЛИ С НЕСКОЛЬКИМИ ВХОДНЫМИ ПЕРЕМЕННЫМИ
Многофакторная (множественная) линейная регрессия

27.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ

28.

ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ РЕГРЕССИОННЫХ МОДЕЛЕЙ
МНОЖЕСТВЕННЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ:

29.

ПОСТАНОВКА И КЛАССИФИКАЦИЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ
.
ОПТИМИЗАЦИЯ – это процесс выбора наилучшего варианта из возможных;
процесс приведения системы/процесса в наилучшее (оптимальное)
состояние.
КРИТЕРИЙ
ОПТИМАЛЬНОСТИ
(КРИТЕРИЙ
ОПТИМИЗАЦИИ)
–
это
количественный или порядковый показатель, выражающий предельную
меру экономического эффекта принимаемого решения для сравнительной
оценки возможных решений (альтернатив) и выбора наилучшего.

30.

ПОСТАНОВКА И КЛАССИФИКАЦИЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ

31.

ПОСТАНОВКА И КЛАССИФИКАЦИЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ
Запись ограничений
2 типа ограничений:
1) Ограничения на диапазон проектных переменных (геометрические
ограничения)
2) Функциональные ограничения, связанные с работоспособностью
проектируемой системы.
Ограничения записываются в стандартной форме:

32.

ПОСТАНОВКА И КЛАССИФИКАЦИЯ ЗАДАЧ УСЛОВНОЙ ОПТИМИЗАЦИИ
Численные методы оптимизации
2 этапа алгоритма решения задачи оптимизации:
1) Вычисление характеристик задачи;
2) По полученной информации строится приближение к решению.
Для задания алгоритма нужно указать способ выбора точек
приближения

33.

ЗАДАЧИ ДИСКРЕТНОЙ ОПТИМИЗАЦИИ И ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ

34.

ЗАДАЧИ ДИСКРЕТНОЙ ОПТИМИЗАЦИИ И ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Динамическое программирование – это математический метод для
нахождения оптимальных решений многошаговых (многоэтапных)
задач оптимизации.
Аддитивная функция:
Принцип оптимальности и уравнение Беллмана: