Постановка и возможные подходы к решению задачи об определении движения точек механической системы

1.

Постановка и возможные подходы к решению задачи
об определении движения точек механической системы
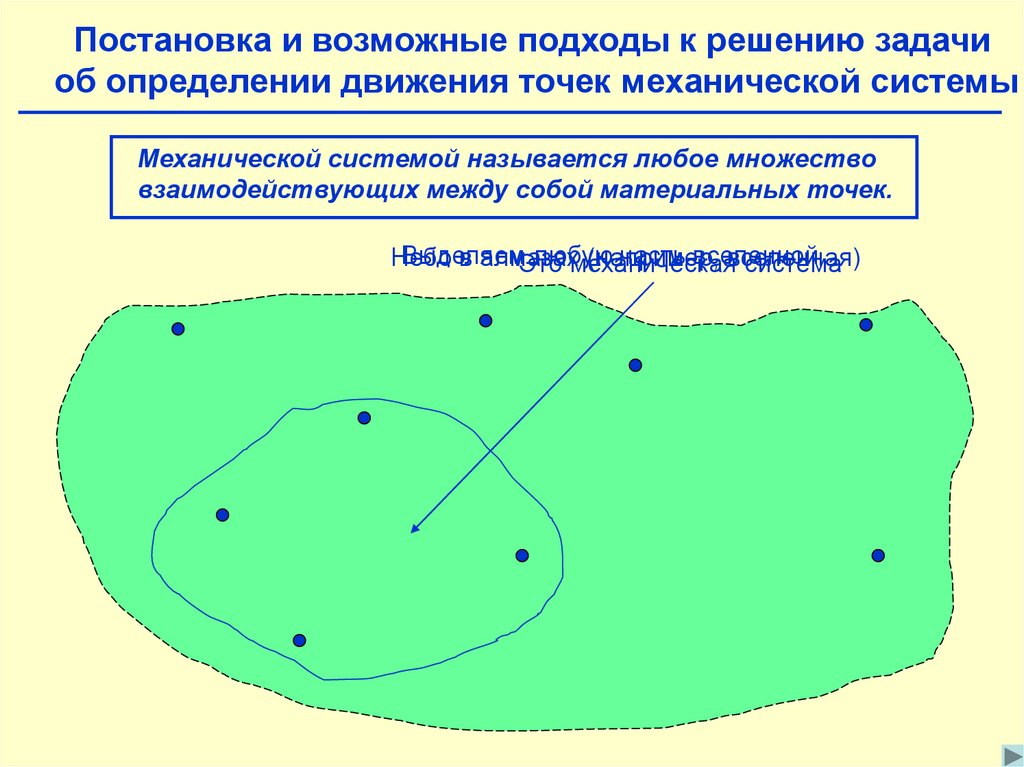
Механической системой называется любое множество
взаимодействующих между собой материальных точек.
Выделяем
любую
часть вселенной
Небо
в алмазах
(например,
вселенная)
Это
механическая
система

2.

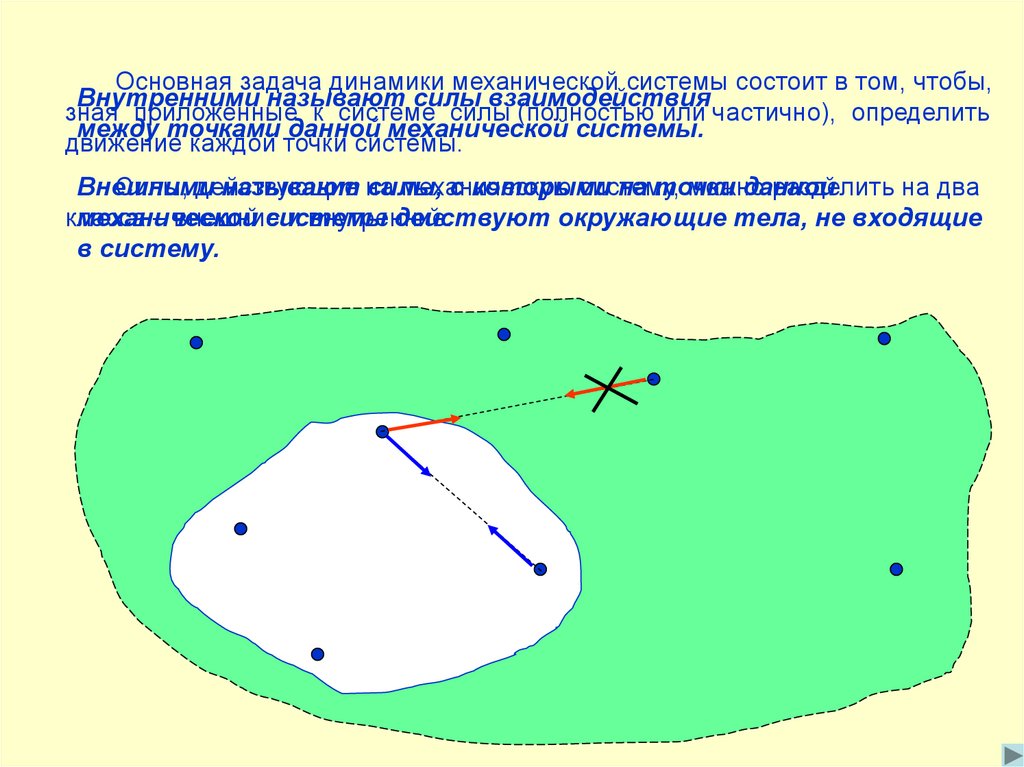
Основная задача динамики механической системы состоит в том, чтобы,
Внутренними называют силы взаимодействия
зная приложенные к системе силы (полностью или частично), определить
между точками данной механической системы.
движение каждой точки системы.
Силы, действующие
механическую
систему,
можно
разделить на два
Внешними
называют на
силы,
с которыми
на точки
данной
класса
– внешние
и внутренние.
механической
системы
действуют окружающие тела, не входящие
в систему.

3.

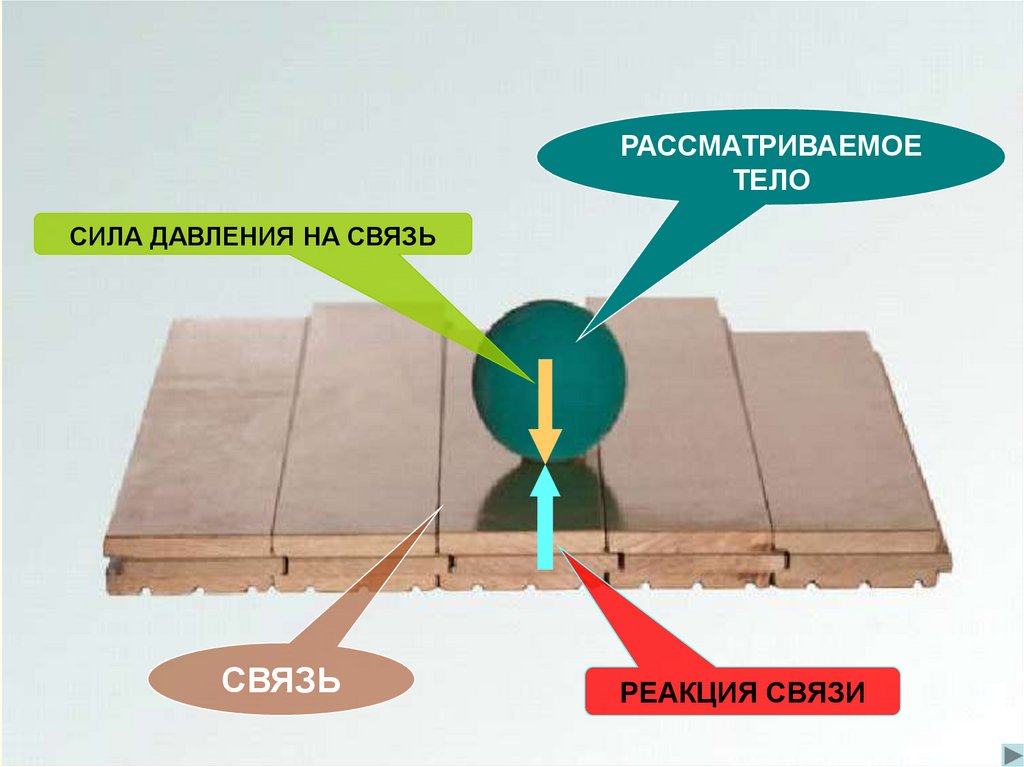
С другой стороны силы разделяют на активные и реакции связей.
Реакциями связей называют силы, с которыми на точки
механической системы действуют наложенные на них связи.
Силы, не являющиеся реакциями связей,
называют активными силами или заданными силами.

4.

РАССМАТРИВАЕМОЕ
ТЕЛО
СИЛА ДАВЛЕНИЯ НА СВЯЗЬ
СВЯЗЬ
РЕАКЦИЯ СВЯЗИ

5.

Рассмотрим механическую систему, состоящую из n материальных точек.
Пусть система движется относительно некоторой инерциальной системы
отсчета. Для любой точки механической системы справедлив второй закон
Ньютона:
d 2 rk
mk 2 Fke Fki
dt
k 1 2 n
(1)
где
mk – масса точки с номером k :
rk
– её радиус–вектор;
Fke – равнодействующая всех внешних сил, как активных,
Fki
так и реакций внешних связей, действующих на точку с номером k;
– равнодействующая всех внутренних сил, действующих на точку с
номером k .
Система уравнений (1) называется системой дифференциальных
уравнений движения точек механической системы.