Similar presentations:
Булеві функції
1. Булеві функції
12. Як задавати функції
аналітичнотаблично
2
y=x
X
1
2
3
Y=X2
1
4
9
x
1
2
3
y=(x-1)(x-2)(x+1.5)+
+(x-1)(x-3)(x-6)+(x-2)(x-3)(x-⅟2)
1
4
9
3.
Означення Булева функціяn-арною (залежною від n змінних)
булевою функцією Fn будемо називати функцію, яка діє з
n-го декартового степеню множини булевих значень
{0;1}
в множину булевих значень {0;1}
n
Fn:{0;1} {0;1}
Означення Елементи множини {0;1}n будемо
називати булевими векторами або булевими
наборами (x1,x2,…xn), де xi {0;1} довжини n.
3
4.
nЛема. Існує 2 булевих наборів
довжини n.
( x1 , x2 , ..... xn )
0,1
0,1
0,1
2 2 ........ 2 2
n разів
n
4
5. Лема 3.4. Існує 22n різних булевих ф-й n змінних.
n2
Лема 3.4. Існує 2 різних булевих
ф-й n змінних.
2n
x1
x2
…
xn
f
0
0
…
0
{0,1}
0
0
…
1
{0,1}
…
…
…
…
…
1
1
…
1
{0,1}
2 2 ...... 2 2
n
2 разів
n
2
5
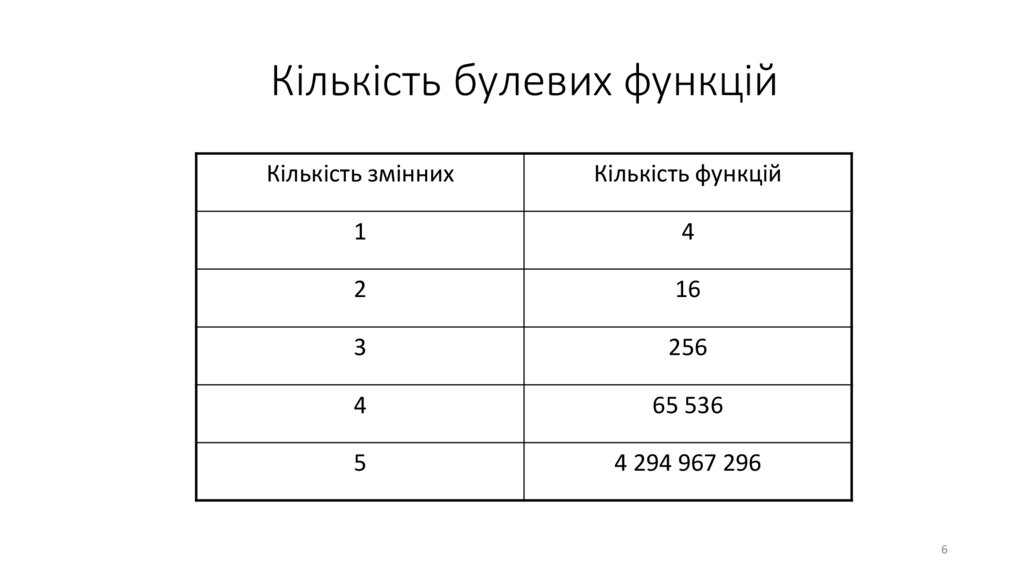
6. Кількість булевих функцій
Кількість зміннихКількість функцій
1
4
2
16
3
256
4
65 536
5
4 294 967 296
6
7. Означення Суперпозиція булевих функцій
Функція F(x1,x2,..xn) називаєтьсясуперпозицією функції f0(z1,z2,…zk), та
функцій fi(x1,x2,…xn) i=1…k якщо вона є
результатом підстановки значень
функцій fi(x1,x2,…xn) замість значень
змінних zi функції f0(z1,.z2,…zk):
F(x1,x2,..xn) =
= f0(f1(x1,x2,…xn),… ,fk(x1,x2,…xn))
7
8. Суттєва залежність функції від змінних
f(x)=(x+2)2-4x-x2 начебто залежить від x. Насправді, післяелементарних перетворень маємо:
f(x)=(x+2)2-4x-x2 =x2+4x+4-4x-x2 =4
f(x) насправді незалежить від x
g(x,y)=(2x+y)2-4xy-y2=4x2
залежить від x, не залежить від y
10/17/20
9. Означення. Суттєва змінна
Змінна xk суттєва для f(x1,x2,…xn),якщо існують 2 набори
( 1, 2,… k,… n) та ( 1, 2,… k,… n),
такі що k ≠ k та
f( 1, 2,… k,… n) ≠ f( 1, 2,… k,… n)
Означення Функція, в якої є несуттєві змінні
називається виродженою
9
10. Задання функції таблицею
АргументиФункція
Значення аргументів 1
Значення функції для аргументів 1
Значення аргументів 2
Значення функції для аргументів 2
Значення аргументів 3
Значення функції для аргументів 3
…………………………
…………………………
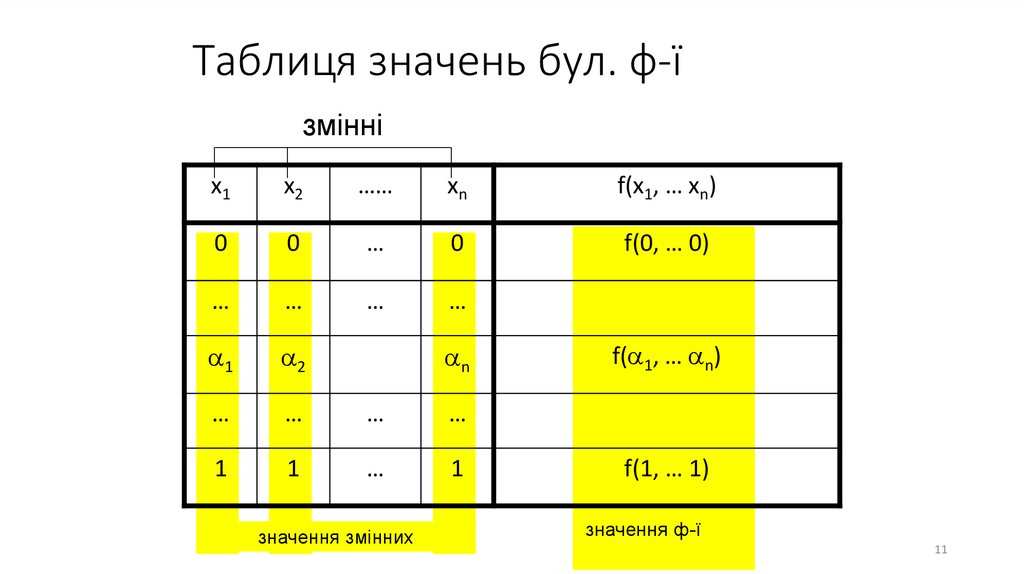
11. Таблиця значень бул. ф-ї
змінніx1
x2
……
xn
f(x1, … xn)
0
0
…
0
f(0, … 0)
…
…
…
…
1
2
…
…
…
…
1
1
…
1
n
значення змінних
f( 1, … n)
f(1, … 1)
значення ф-ї
11
12. Ф-ї однієї змінної
Функції двох змінних*
*
*
*
*
*
x y 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
000000000011111111
010000111100001111
100011001100110011
110101010101010101
* - вироджені функції
13
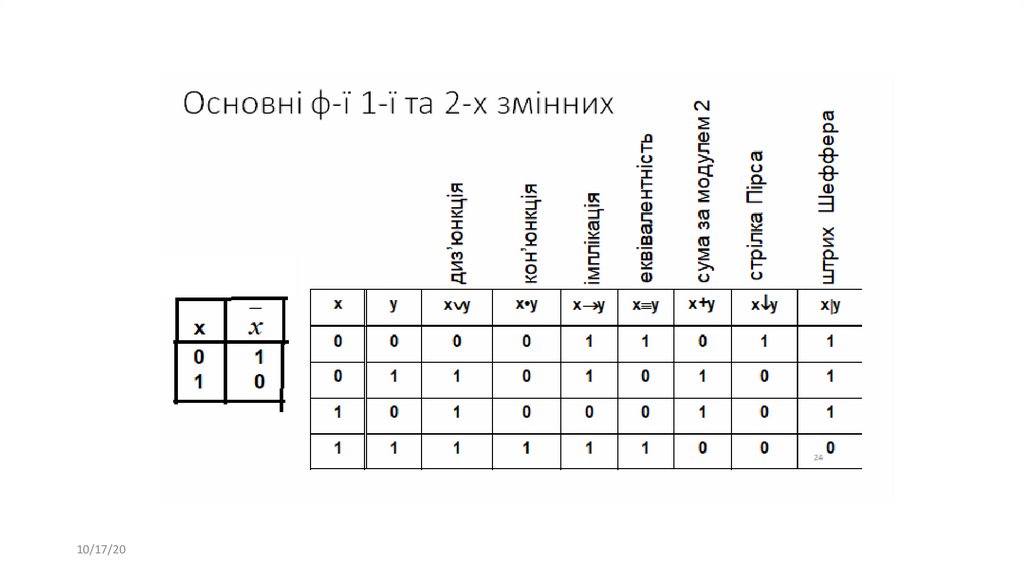
13. Функції двох змінних
Невироджені ф-ї 2-х змінних,
1-кон‘юнкція &,
7-диз‘юнкція
11,13-імплікація
9-еквівалентність
6-сума за модулем 2 ,
8-стрілка Пірса
14-штрих Шефера
2,4-функції заборони
(заперечення імплікації)
14
14. Невироджені ф-ї 2-х змінних
10/17/2015.
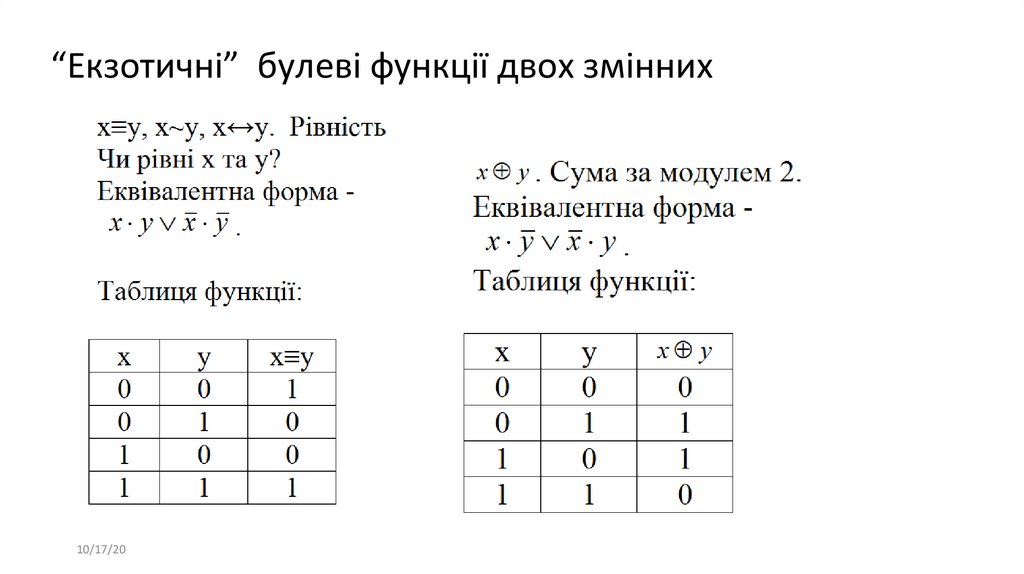
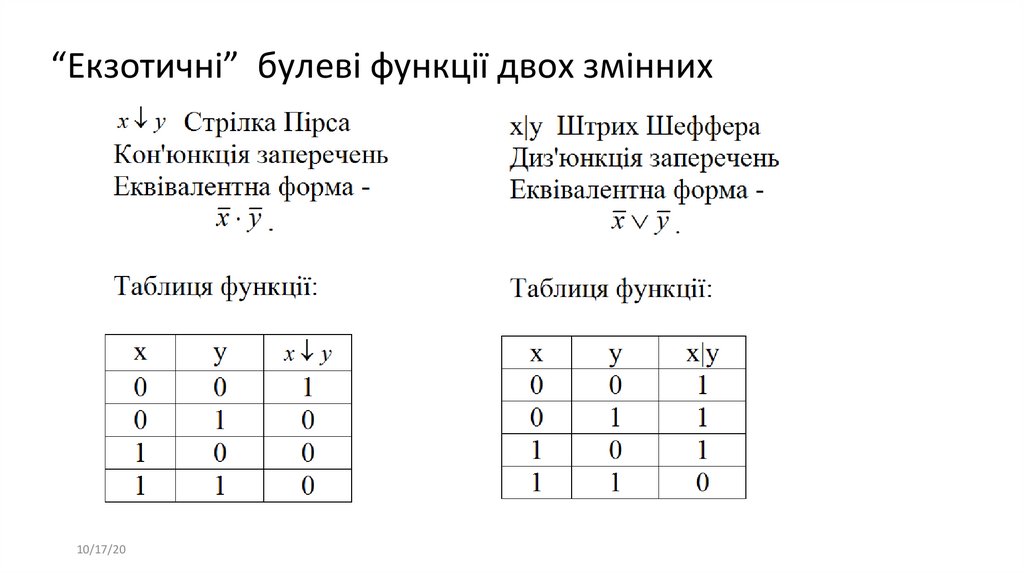
“Екзотичні” булеві функції двох змінних10/17/20
16.
“Екзотичні” булеві функції двох змінних10/17/20
17.
“Екзотичні” булеві функції двох змінних10/17/20
18.
Зводна таблиця10/17/20
19.
Тотожності для бул. ф-йx y=y x, x y=y x перестановочність/комутативність
x (y z)=(x y) z - сполучність/асоциативність
x (y z)=(x y) z
x (y z)=x y x z - розподільність/дистрибутивність
x y z=(x y) (x z)
x x, 0 1, 1 0
x x x, x x x ідемпотемність
x y x y,
x y x y правила де Моргана
20
20. Тотожності для бул. ф-й
x x 1, x x 0, Правила поглинанняx 0 x, x 1 1
x 0 0, x 1 x
A A B A, A ( A B) A
A A B A B, A A B A B
21
21. Тотожності для бул. ф-й
Графічна інтерпретація булевих функційФункції двох змінних - квадрат
10/17/20
22. Графічна інтерпретація булевих функцій
Функції двох змінних - квадрат10/17/20
23. Графічна інтерпретація булевих функцій
Функції двох змінних – квадратДля булевої функції двох змінних виділимо на квадраті вершини, в
яких функція набуває значення 1:
10/17/20
24. Графічна інтерпретація булевих функцій
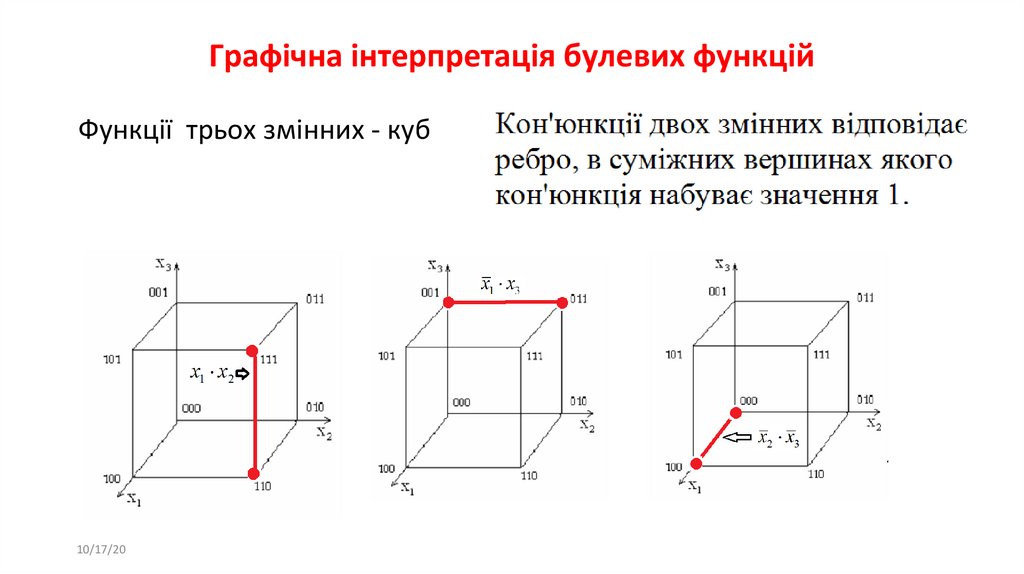
Функції трьох змінних - куб10/17/20
25. Графічна інтерпретація булевих функцій
Функції трьох змінних - куб10/17/20
26. Графічна інтерпретація булевих функцій
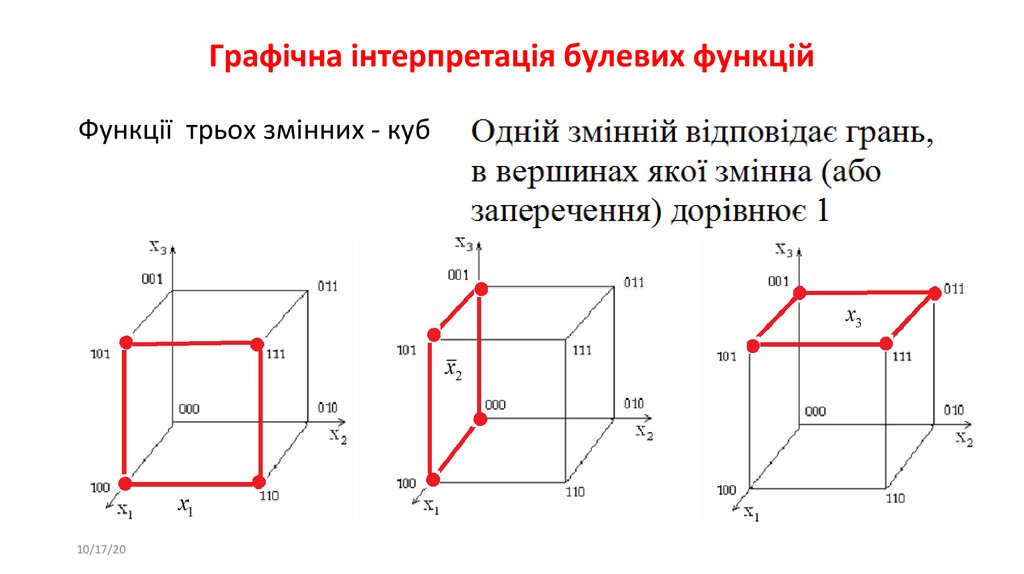
Функції трьох змінних - куб10/17/20
27. Графічна інтерпретація булевих функцій
Правило Заповненнятаблиці значень n змінних
• Таблиця має 2n рядків (без заголовку)
• 1-й зліва стовпчик ділиться навпіл. Верхня половина
заповнюється нулями, нижня – одиницями.
• Кожна частина попереднього стовпчика ділиться навпіл. В
утворені частини по черзі записуються нулі та одиниці.
28
28. Правило Заповнення таблиці значень n змінних
Правило 3.8. Заповненнятаблиці значень n змінних
• Таблиця має 2n рядків (без заголовку)
Або так:
• 1-й справа стовпчик 0-1-0-1,…
• 2-й справа стовпчик 00-11-00-11,…
• 3-й справа стовпчик 0000-1111-0000-1111
і т.д, далі нулі з 1 чергуються через 8, потім через 16, …
29
29. Правило 3.8. Заповнення таблиці значень n змінних
Диз’юнктивні такон’юнктивні
нормальні форми
булевих функцій
31
30. Побудова таблиці значень бул. ф-ї
Означення 3.9. Елементарні(диз’юнкції) кон’юнкції
ЕД (ЕК) будемо називати диз'юнкцію
(кон'юнкцію) попарно різних змінних або їх
заперечень
Елементарні диз’юнкції (ЕД)
0, x1 , x y, a b c
Елементарні кон’юнкції (ЕК)
1, x, x1 x3 , x yz
32
31. Диз’юнктивні та кон’юнктивні нормальні форми
Елементарні диз'юнкції та кон'юнкціїЧому попарно різні змінні?
xyzx xyzy xyz
xyzx xyzy 0
33
32. Означення 3.9. Елементарні (диз’юнкції) кон’юнкції
Елементарні диз'юнкції та кон'юнкціїx yz yzx xz y zx y
Домовленість ЕД (ЕК) які відрізняються
тільки порядком змінних будемо
вважати однаковими
(так само, як і добутки (суми) в алгебрі)
34
33. Елементарні диз'юнкції та кон'юнкції
Означення Диз'юнктивні (кон'юнктивні)нормальні форми
Диз'юнктивною нормальною формою булевої
ф-ї f (скорочено ДНФ)
будемо називати її представлення у вигляді
диз'юнкції попарно різних елементарних
кон'юнкцій.
Кон'юнктивною нормальною формою булевої ф-ї f
(скорочено КНФ) будемо називати її
представлення у вигляді кон'юнкції попарно різних
елементарних диз'юнкцій.
35
34. Елементарні диз'юнкції та кон'юнкції
x x y yzднф
( x y) ( y z) z
кнф
xy x z yx
x y x y x y x y
36
35. Означення Диз'юнктивні (кон'юнктивні) нормальні форми
Побудова ДНФ перетвореннями( x y) ( x y) ( x y ( y z ))
( x y) ( x y) ( x y ( y z ))
( x y) ( x y) x y ( y z)
xx y yx y x y y x y z
x y 0 x y x yz
xy xyz
днф
37
36.
Означення Повні елементарні кон'юнкції(диз'юнкції)
Елементарна кон'юнкція (диз'юнкція)
називається повною (скорочено ПЕК або
ПЕД) відносно множини змінних {x1,x2, … xn},
якщо до неї входять, з запереченням чи без,
всі змінні x1,x2, … xn.
38
37. Побудова ДНФ перетвореннями
Означення. Досконалі диз'юнктивні(кон'юнктивні) нормальні форми
Диз'юнктивну нормальну форму булевої
функції f(x1,x2, … xn) будемо називати
досконалою (скорочено ДДНФ), якщо
всі її елементарні кон'юнкції є повними
відносно множини змінних {x1,x2, … xn}
Кон'юнктивну нормальну форму булевої
функції f(x1,x2, … xn) будемо називати
досконалою (скорочено ДКНФ), якщо всі її
елементарні диз'юнкції є повними відносно
множини змінних {x1,x2, … xn}
39
38. Означення Повні елементарні кон'юнкції (диз'юнкції)
Побудова ДДНФ за таблицею41
39. Означення. Досконалі диз'юнктивні (кон'юнктивні) нормальні форми
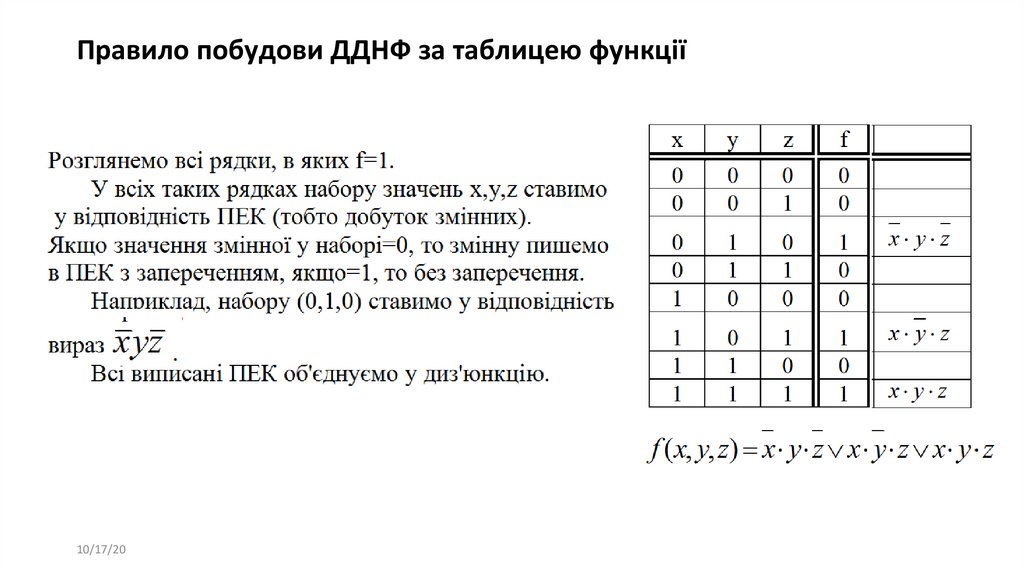
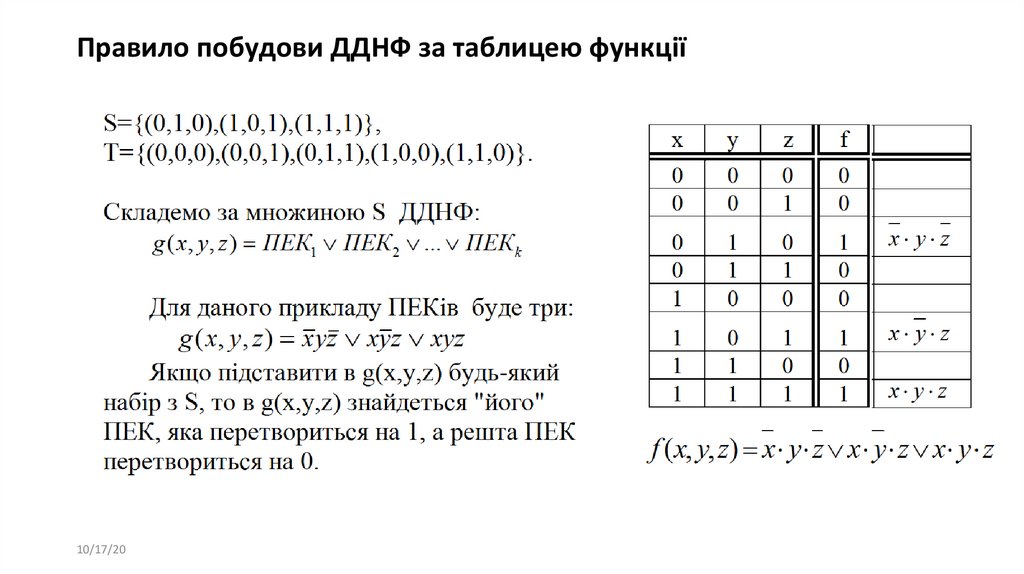
Правило побудови ДДНФ за таблицею функції10/17/20
40. Побудова ДДНФ перетвореннями
Правило побудови ДДНФ за таблицею функції10/17/20
41. Побудова ДДНФ за таблицею
Правило побудови ДДНФ за таблицею функції10/17/20
42. Правило побудови ДДНФ за таблицею функції
10/17/2043. Правило побудови ДДНФ за таблицею функції
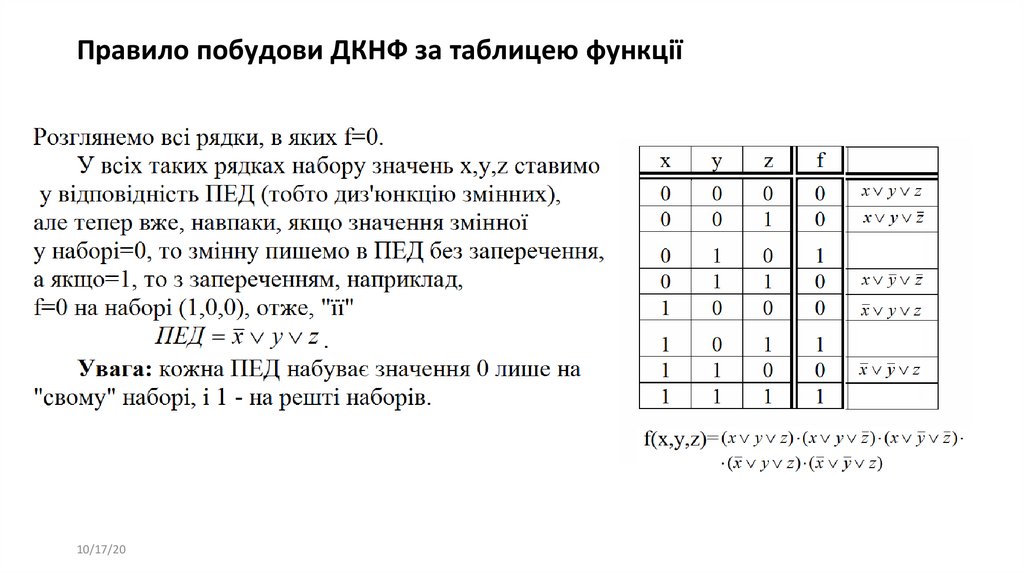
Правило побудови ДКНФ за таблицею функції10/17/20
44. Правило побудови ДДНФ за таблицею функції
Правило побудови ДКНФ за таблицею функції10/17/20
45. Правило побудови ДДНФ за таблицею функції
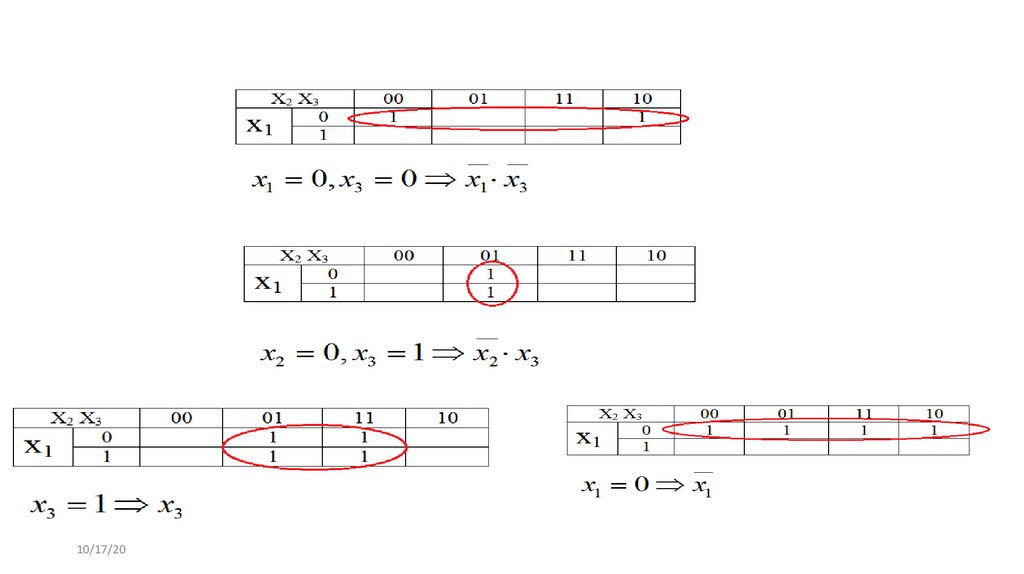
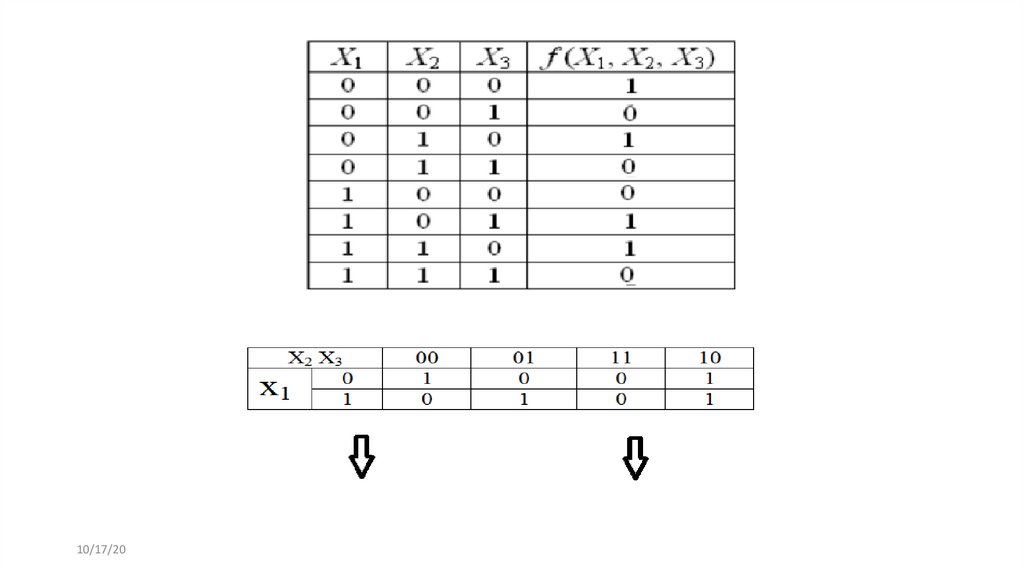
Карти Карно – це діаграми, за допомогою яких можна знайти записДНФ булевої функції у більш простому вигляді, ніж ДДНФ.
Карта Карно для Булевої функції трьох змінних
10/17/20
46. Правило побудови ДКНФ за таблицею функції
Основна ідея – перенести одинички булевої функції з таблиці на карту і об’єднувати сусідніодинички – по 2 або по 4.
Двом сусіднім одиничкам відповідає ДНФ від двох змінних, чотирьом- від однієї.
Прим. 1-й та 4-й стовпець вважаємо сусідніми,
наче карта згорнута в трубочку.
10/17/20






































 mathematics
mathematics








