Similar presentations:
Термины и определения теории фильтрации (лекция 5)
1.
Лекция №5 (к работе №4)Рассматриваемые темы:
Тема 11. Термины и определения теории фильтрации.
Тема 12. Закон Дарси для изотропных и анизотропных сред.
Тема 13. Уравнение неразрывности. Его физически смысл.
Тема 14. Математическая модель течения однофазной жидкости в пористой
среде.
Тема 15. Численная схема решения модели течения однофазной жидкости в
пористой среде.
1
2.
Тема 11. Термины и определения теории фильтрации.Пористая среда:
1) система с большим количеством твердых частиц, плотно прилегающих друг к
другу, сцементированных или нет;
2) пространство между частицами может быть заполнено жидкостью или газом;
3) ее можно рассматривать как систему с большим числом элементов слабо
связанных между собой .
Такие системы не выражаются через свойства составляющих их элементов, а
являются усредненными характеристиками больших объемов пористых сред –
это основная особенность ячеек.
2
3.
Тема 11. Термины и определения теории фильтрации.Пористость m – отношение объема, занятого порами к общему
объему образца. Повторимся – это интегральное или среднее для
объема образца (ячейки) значение. 0 < m < 1 .
Различают полную и эффективную пористость. Эффективная
пористость учитывает только открытые, т.е. проницаемые для
флюида поры. Эффективная пористость меньше полной пористости.
Зерна + поры
Поровое пространство
3
4.
Тема 11. Термины и определения теории фильтрации.Просветность n – характеристика сечения (двухмерного среза),
вычисляемая, как отношение площади пор Δwn к общей площади
среза Δw . 0 < n < 1
скелет
поры
поры
скелет
4
5.
Тема 11. Термины и определения теории фильтрации.Фильтрация – движение жидкости в пористой среде.
Скорость фильтрации un
un n
u
u
n
w
Q
lim
w 0 w
Q – объемный расход жидкости (м3);
Δw – площадь сечения (м2).
Размерность: un =[м/c]
ВАЖНО! Скорость фильтрации un не является действительной или
истинной скоростью движения жидкости, т.к. расход делится на
площадь всего сечения
Скорость фильтрации un всегда меньше
un
Q
vn lim
; vn
u n n vn
действительной скорости vn, т.к.
w
n
w 0
n
просветность n<1
5
6.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Закачка воды
Входное сечение
Напор Hin
Непроницаемая
стенка
Образец
ΔL
Непроницаемая
стенка
Напор Hout
Отбор воды, измерение
расхода Q
Выходное сечение с
площадью Ω
Установка для исследования течения воды через песчаные фильтры
Анри Дарси делал эксперименты для нужд водоснабжения города Дижона (Франция)
6
7.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Порядок проведения фильтрационного эксперимента:
1) Изготавливался образец песчаного фильтра, все эффективные поры
заполнялись водой;
2) Образец помещался в кожух с непроницаемыми внешними стенками, входная
и выходная торцевые границы являлись открытыми;
3) Между входной и выходной границами создавалась разность напоров
Hin– Hout > 0,на входное сечение подавалась вода и за счет разности напоров
фильтровалась через образец;
4) Жидкость отбиралась через выходное сечение площадью Ω, при этом
измерялся расход жидкости Q.
7
8.
Тема 12. Закон Дарси для изотропных и анизотропных сред.В результате многочисленных экспериментов была
установлена следующая зависимость:
Q kф
H
, H H out H in
L
Коэффициент фильтрации: k ф
k g
[м/с]
Коэффициент абсолютной проницаемости k – способность пористых сред
пропускать через себя флюид. Единицы измерения: [мкм2].
Вязкость – свойство жидкостей и газов оказывать сопротивление перемещению
одной их части относительно другой.
Различают динамическую вязкость μ [Па*с] и кинематическую вязкость η [м2/c].
Внесистемная единица:
1 сПз (сантипуаз) = 1мПа*с
μводы=1сПз
Их связь:
8
9.
Тема 12. Закон Дарси для изотропных и анизотропных сред.u
Q
g H
k
, g H p – перепад давления
L
u
k p
Это конечная форма закона Дарси
L
Крайне важные замечания:
1) коэффициент абсолютной проницаемости k является характеристикой только структуры порового
пространства и не зависит от свойств флюида;
2) внесистемной единицей измерения k является Дарси [Да]: 1 Да = 1 мкм2. Проницаемость
традиционных коллекторов находится в пределах от 10 мДа до 10 Да;
3) знак минус в законе Дарси говорит о том, что, поскольку Δp < 0, жидкость течет в сторону уменьшения
давления;
4) закон Дарси в данной форме пригоден только для однофазных течений, т.е. при абсолютном
совпадении свойств вытесняемой и вытесняющей жидкостей;
5) коэффициент фильтрации характеризует свойства и жидкости, и пористой среды. Он пригоден только
для исследования гидрогеологических процессов, т.е. при неизменности свойств жидкости (плотности и
вязкости). В остальных случаях, например, при нефтегазодобыче, им не пользуются.
9
10.
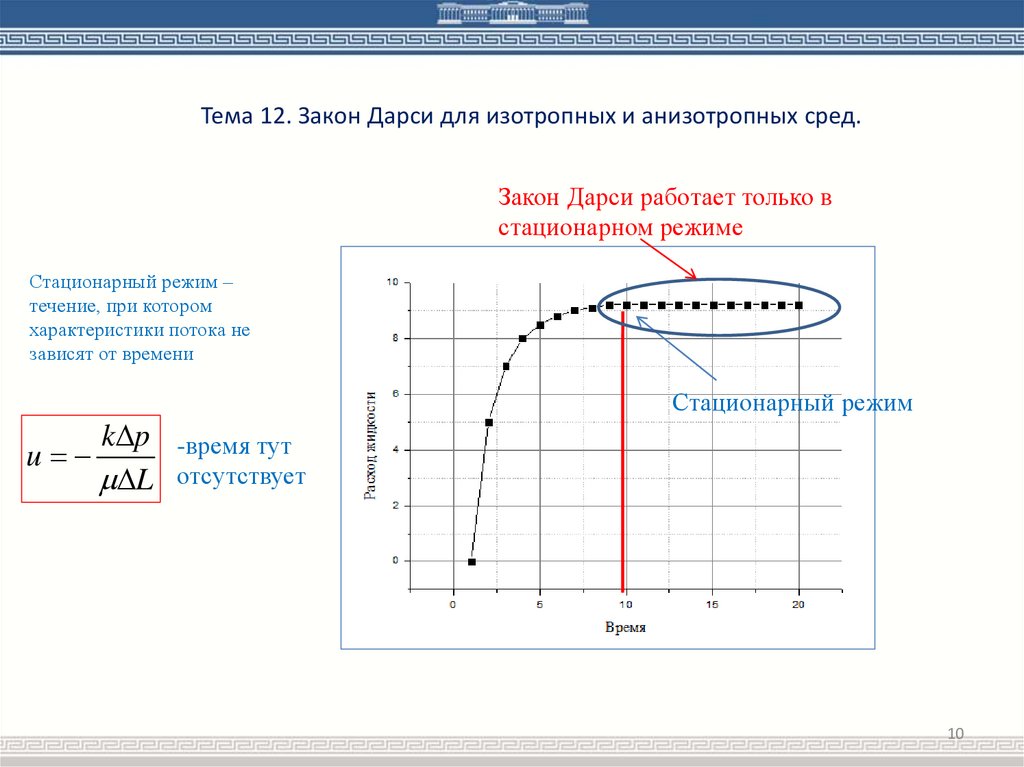
Тема 12. Закон Дарси для изотропных и анизотропных сред.Закон Дарси работает только в
стационарном режиме
Стационарный режим –
течение, при котором
характеристики потока не
зависят от времени
u
k p -время тут
L отсутствует
Стационарный режим
10
11.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Задача о проницаемости цилиндрического капилляра
(первый решивший получит 5 баллов).
Вычислить радиус цилиндрического капилляра, при
котором его проницаемость равна 1 Да?
11
12.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Обобщенный закон Дарси в трехмерном пространстве имеет
следующий вид:
k
P P P
u gradP; gradP
i
j
k
x
y
z
i, j, k – единичные базисные векторы системы координат.
Есть проблема! В общем случае скорость фильтрации не совпадает с
направлением градиента давления.
gradP
u
12
13.
Тема 12. Закон Дарси для изотропных и анизотропных сред.13
14.
Тема 12. Закон Дарси для изотропных и анизотропных сред.В такой ситуации коэффициент абсолютной проницаемости является
тензорной величиной.
k xx k xy k xz
k k yx k yy k yz
k k k
zx zy zz
k xx k xy k xz P / x
1
u k yx k yy k yz P / y
k k k P / z
zx zy zz
Закон Дарси в проекциях на декартову с/к будет иметь вид:
P
P
P
k xy
k xz
)
x
y
z
1
P
P
P
u y (k yx
k yy
k yz
)
x
y
z
ux
1
uz
1
(k xx
(k zx
P
P
P
k zy
k zz
)
x
y
z
14
15.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Тензор абсолютной проницаемости является симметричным, т.е.
kij=kji: kxy=kyx, kzx=kxz, kzy=kyz .
К счастью, существует такая теорема, согласно которой всегда
можно подобрать такую, в которой недиагональные
компоненты тензора будут равны нулю. Иными словами
любой тензор всегда можно привести к главным осям.
k 0 0
xx
k 0 k yy 0
0 0 k zz
kxx, kyy, kzz – компоненты тензора в главных
осях
15
16.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Закон Дарси можно записать в следующем виде:
ux
k yy P
k P
k xx P
.
; u z zz
; uy
z
y
x
Пористая среда изотропна?
да, kxx=kyy =kzz
нет, kxx≠kyy ≠kzz
Чаще всего kxx=kyy , kzz =γ kxx, γ<1.
16
17.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Примеры
Пористой средой с высокой весовой долей (более 80 %) изотропной
компоненты можно считать песчаники (без трещин).
Главные оси (XYZ)
8,95
0,00
0,00
0,00
8,12
0,00
0,00
0,00
8,56
17
18.
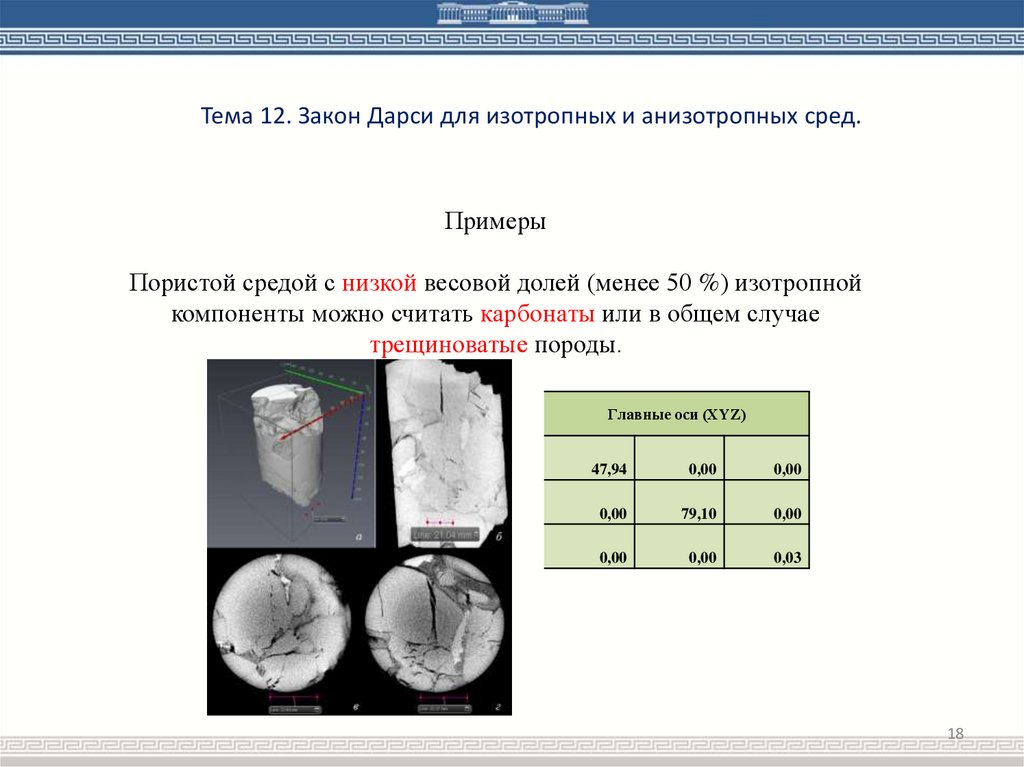
Тема 12. Закон Дарси для изотропных и анизотропных сред.Примеры
Пористой средой с низкой весовой долей (менее 50 %) изотропной
компоненты можно считать карбонаты или в общем случае
трещиноватые породы.
Главные оси (XYZ)
47,94
0,00
0,00
0,00
79,10
0,00
0,00
0,00
0,03
18
19.
Тема 12. Закон Дарси для изотропных и анизотропных сред.Есть фильтрационная установка, которая умеет мерить все, что
вы придумаете: перепады давлений между любыми гранями,
скорости течения в любых направлениях и т.д.
Задача на 15 баллов: придумать алгоритм эксперимента для
измерения тензора абсолютной проницаемости с учетом
недиагональных компонент.
k xx k xy k xz
k k yx k yy k yz
k k k
zx zy zz
19
20.
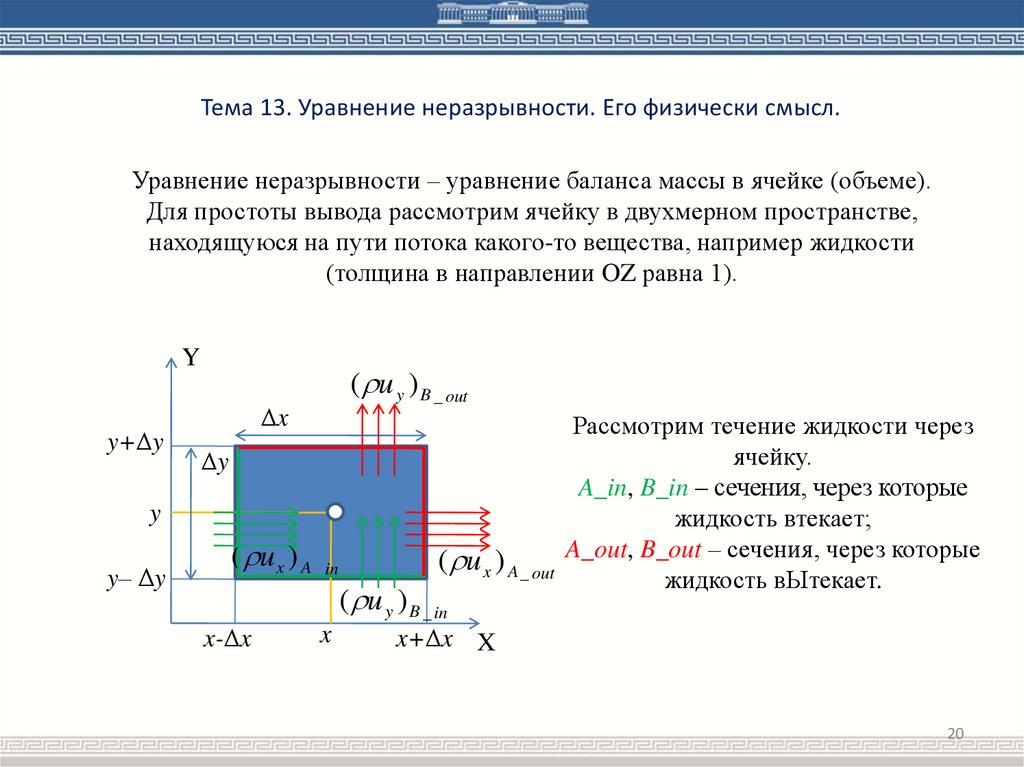
Тема 13. Уравнение неразрывности. Его физически смысл.Уравнение неразрывности – уравнение баланса массы в ячейке (объеме).
Для простоты вывода рассмотрим ячейку в двухмерном пространстве,
находящуюся на пути потока какого-то вещества, например жидкости
(толщина в направлении OZ равна 1).
Y
( u y ) B _ out
Δx
y+Δy
Δy
y
y– Δy
( u x ) A _ in
Рассмотрим течение жидкости через
ячейку.
A_in, B_in – сечения, через которые
жидкость втекает;
( u x ) A _ out A_out, B_out – сечения, через которые
жидкость вЫтекает.
( u y ) B _ in
x-Δx
x
x+Δx X
20
21.
Тема 13. Уравнение неразрывности. Его физически смысл.Y
( u y ) B _ out
Δx
y+Δy
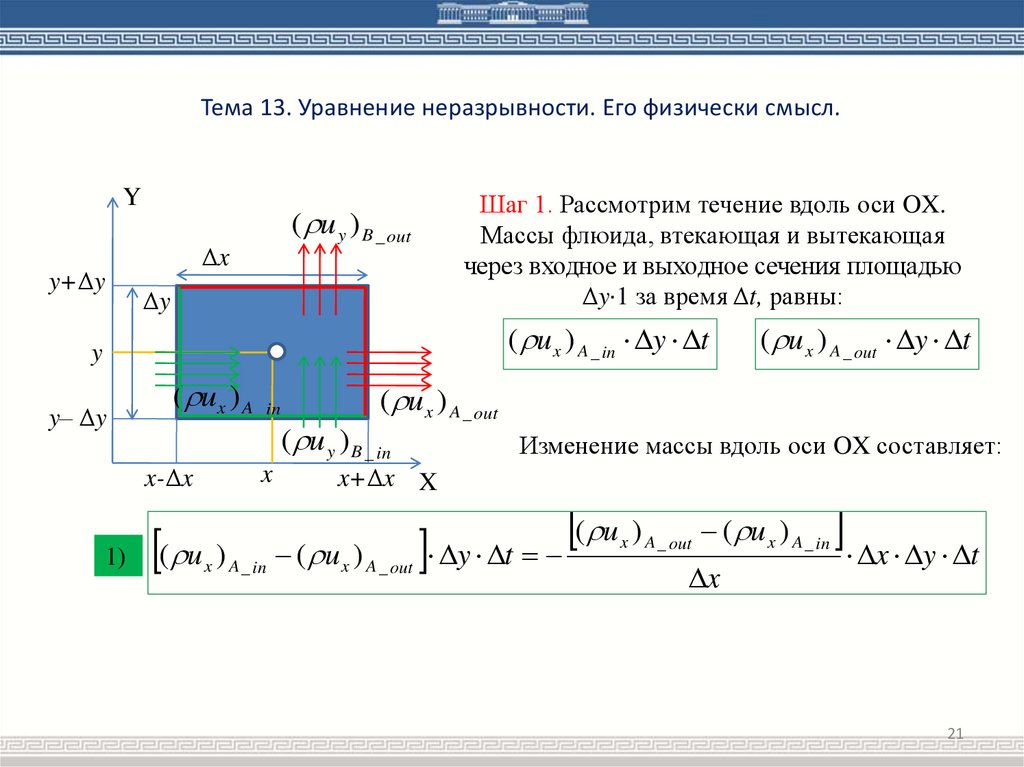
Шаг 1. Рассмотрим течение вдоль оси OX.
Массы флюида, втекающая и вытекающая
через входное и выходное сечения площадью
Δy·1 за время Δt, равны:
Δy
( u x ) A _ in y t
y
y– Δy
( ux ) A _ in
( u x ) A _ out
( u y ) B _ in
Изменение массы вдоль оси OX составляет:
x
x-Δx
1)
( u x ) A _ out y t
( u )
x A _ in
x+Δx X
( u x ) A _ out
( u )
y t
x A _ out
( u x ) A _ in
x
x y t
21
22.
Тема 13. Уравнение неразрывности. Его физически смысл.Y
( u y ) B _ out
Δx
y+Δy
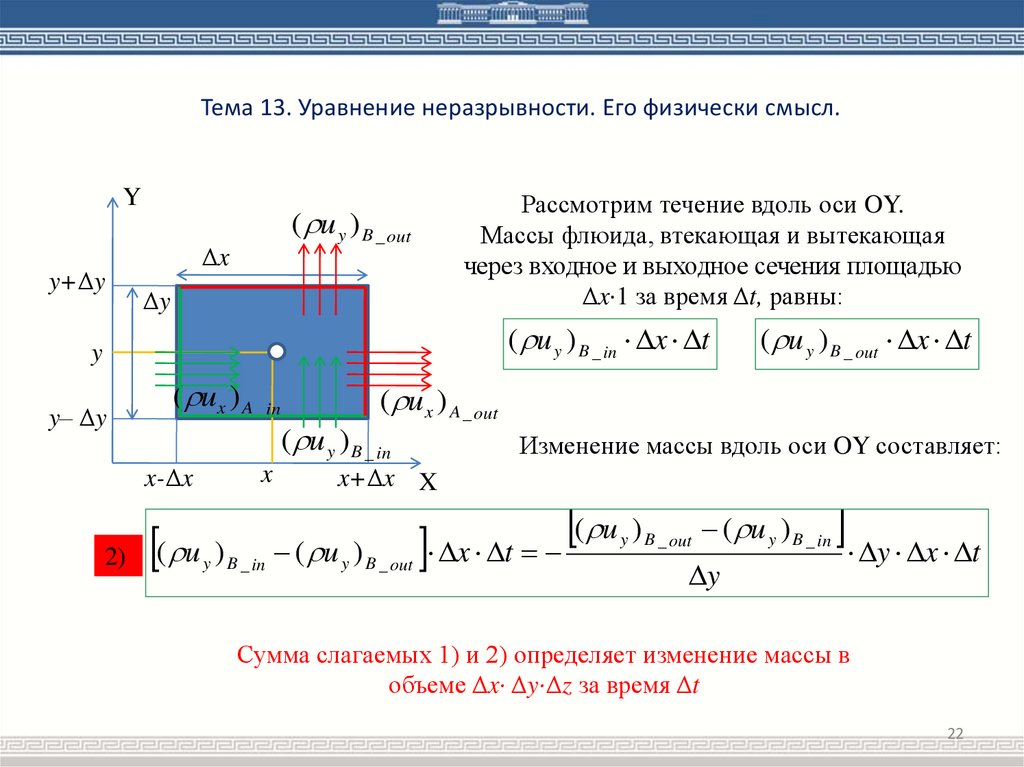
Рассмотрим течение вдоль оси OY.
Массы флюида, втекающая и вытекающая
через входное и выходное сечения площадью
Δx·1 за время Δt, равны:
Δy
( u y ) B _ in x t
y
y– Δy
( ux ) A _ in
( u x ) A _ out
( u y ) B _ in
Изменение массы вдоль оси OY составляет:
x
x-Δx
2)
( u y ) B _ out x t
( u )
y B _ in
x+Δx X
( u y ) B _ out
( u )
x t
y B _ out
( u y ) B _ in
y
y x t
Сумма слагаемых 1) и 2) определяет изменение массы в
объеме Δx· Δy·Δz за время Δt
22
23.
Тема 13. Уравнение неразрывности. Его физически смысл.Y
( u y ) B _ out
Δx
y+Δy
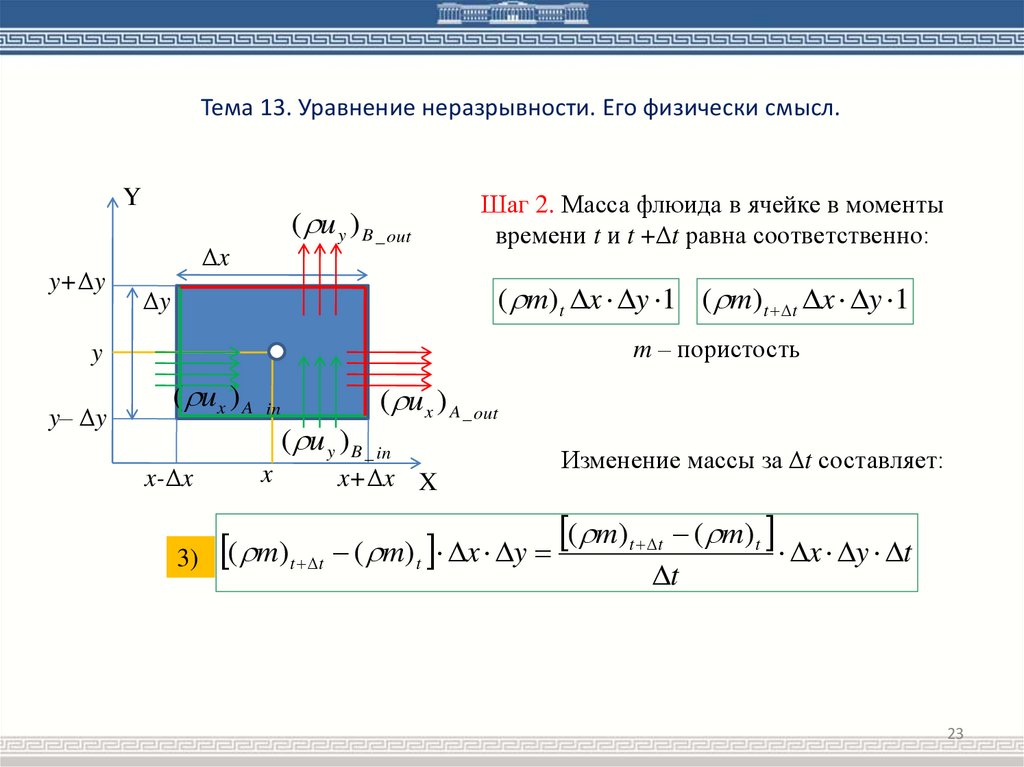
Шаг 2. Масса флюида в ячейке в моменты
времени t и t +Δt равна соответственно:
( m) t x y 1 ( m) t t x y 1
Δy
m – пористость
y
y– Δy
( ux ) A _ in
( u x ) A _ out
( u y ) B _ in
x-Δx
x
x+Δx X
Изменение массы за Δt составляет:
( m)t t ( m)t x y t
(
m
)
(
m
)
x
y
3)
t t
t
t
23
24.
Тема 13. Уравнение неразрывности. Его физически смысл.Шаг 3. Приравниваем сумму уравнений 1) и 2) к уравнению 3:
( u y ) B _ out ( u y ) B _ in
( u x ) A _ out ( u x ) A _ in
( m)t t ( m)t y x t
y x t
x
y
t
Устремляем Δx, Δy, Δt к нулю
div( u )
( m)
t
24
25.
Тема 13. Уравнение неразрывности. Его физически смысл.( m)
div( u )
0
t
Это уравнение неразрывности!
25
26.
Тема 13. Уравнение неразрывности. Его физически смысл.Замечания:
1) Данное уравнение справедливо, когда в ячейке нет источников и стоков
флюидов, т.е. скважин или контуров питания; если они есть то:
( m)
div( u )
q;
t
2) Если жидкость, как вода, несжимаема, то:
div(u ) 0;
3) Данное уравнение можно использовать не только для пористых сред, но и
в случае, когда ячейка является порой:
div( u )
q.
t
26
27.
Тема 13. Уравнение неразрывности. Его физически смысл.Рассмотрим двухмерную ячейку; жидкость течет вдоль оси
OX, остальные грани будем считать закрытыми
(непроницаемыми); жидкость несжимаема.
Распишем уравнение неразрывности для ячейки.
Y
u
u x (u x ) out (u x ) in
div(u ) x
0
x
x
x
y
(u x ) in
(u x ) out (u x ) in
(u x ) out
x
X
(u x ) out y 1 (u x ) in y 1
Сколько в ячейку втекает жидкости, столько и вытекает!
Справедливо только для несжимаемых жидкостей и в отсутствии
источников.
27
28.
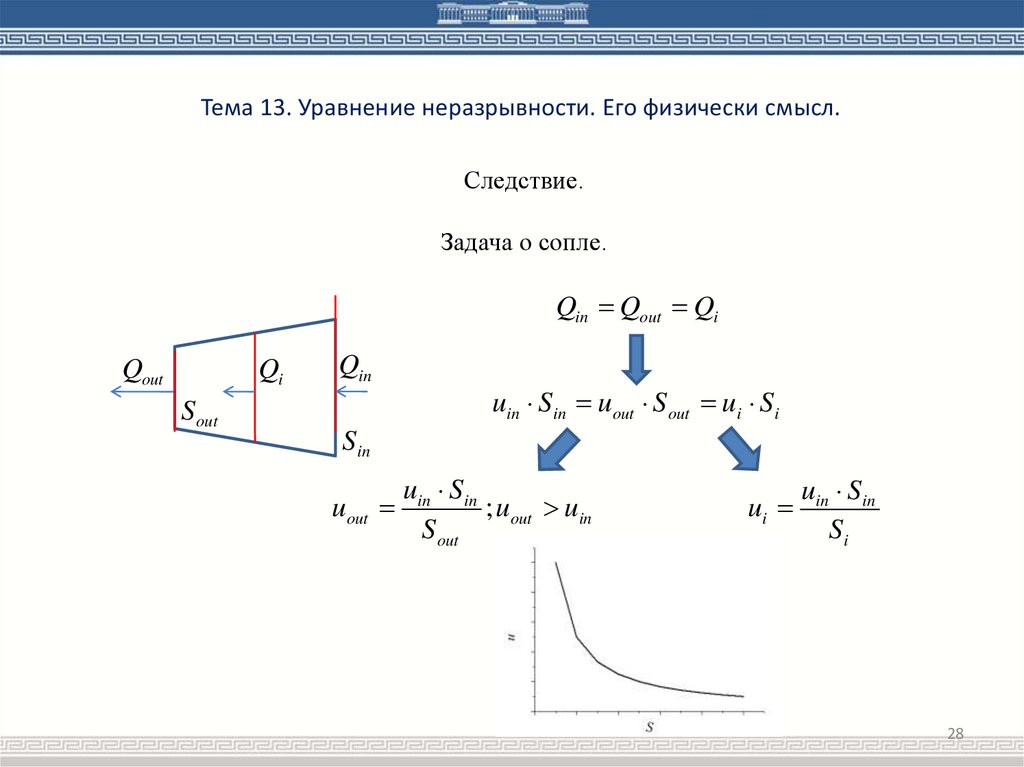
Тема 13. Уравнение неразрывности. Его физически смысл.Следствие.
Задача о сопле.
Qin Qout Qi
Qout
Qi
Qin
S out
uin Sin uout S out ui Si
Sin
uout
uin Sin
; uout uin
S out
ui
uin Sin
Si
28
29.
Тема 14. Математическая модель течения однофазной жидкостив пористой среде.
Вводные замечания
Есть элемент пористой среды, который насыщен жидкостью. Из
пористой проводится вытеснение жидкости путем нагнетания
жидкости с идентичными свойствами. Иными словами масло
вытесняет масло или вода вытесняет воду. Имеем дело только с
одной жидкостью. Такая фильтрация называется однофазной.
нагнетание
На вход подается вода
вытеснение
На выходе отбирается
тоже вода
29
30.
Тема 14. Математическая модель течения однофазной жидкостив пористой среде.
Рассмотрим простейший случай однофазной изотермической
фильтрации несжимаемой жидкости.
Математической моделью такого течения является:
а) система дифференциальных уравнений в частных
производных
+
б) граничные и начальные условия.
1)div(u ) 0
2)u x
*
3)u y
k xx P
x
k yy P
y
k P
4)u z zz
z
Уравнение неразрывности
Температура
скелета и
всех
жидкостей
одинакова и
не меняется
при
проведении
испытаний
Закон Дарси (если 3D)
30
31.
Тема 14. Математическая модель течения однофазной жидкостив пористой среде.
Задачи, в которых известны свойства флюидов,
геометрические характеристики области фильтрации и ее
фильтрационно-емкостные свойства, называют прямыми.
Такие задачи решаются в переменных «скорость-давление»:
u x ( x, y , z ) u y ( x, y , z ) u z ( x, y , z ) p ( x, y , z )
Задачи, в которых известны свойства флюидов, распределение
скорости и давления, а также геометрические характеристики
области фильтрации, называют обратными.
Для таких задач неизвестными считаются фильтрационные
свойства области фильтрации.
Мы будем рассматривать только ПРЯМЫЕ задачи.
31
32.
Тема 14. Математическая модель течения однофазной жидкостив пористой среде.
В представленной математической модели используется закон
Дарси. Он применим только для стационарных течений.
Поэтому система уравнений не содержит временной параметр
t и от времени не зависит.
Начальных условий в данной постановке задачи нет!
32
33.
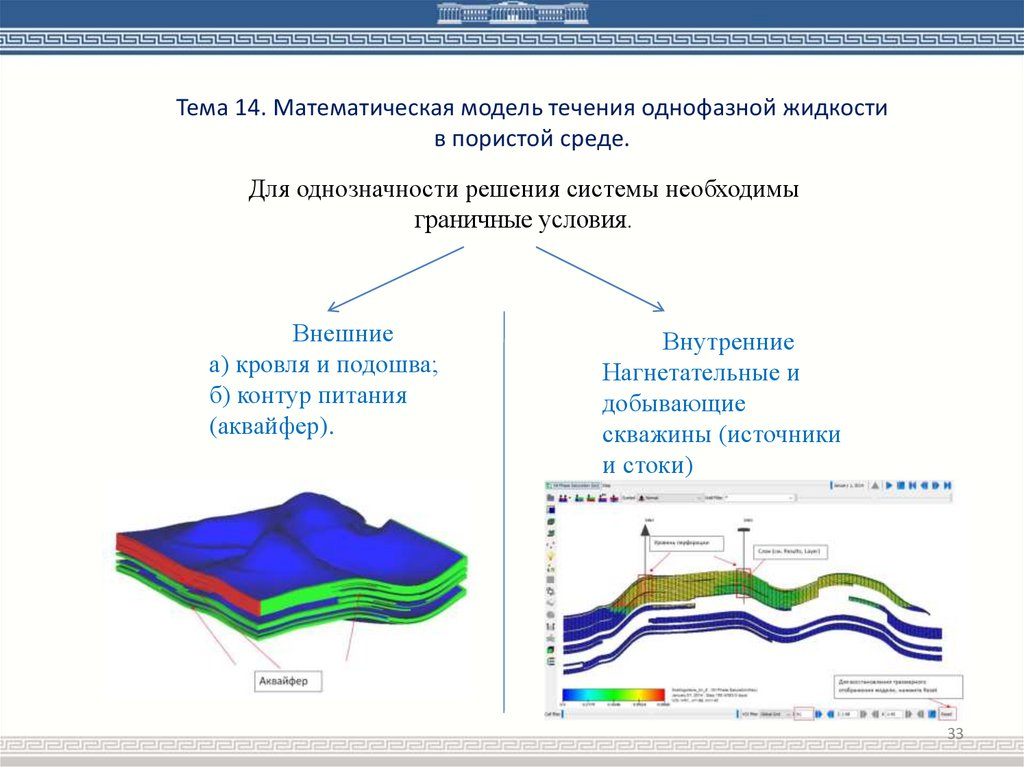
Тема 14. Математическая модель течения однофазной жидкостив пористой среде.
Для однозначности решения системы необходимы
граничные условия.
Внешние
а) кровля и подошва;
б) контур питания
(аквайфер).
Внутренние
Нагнетательные и
добывающие
скважины (источники
и стоки)
33
34.
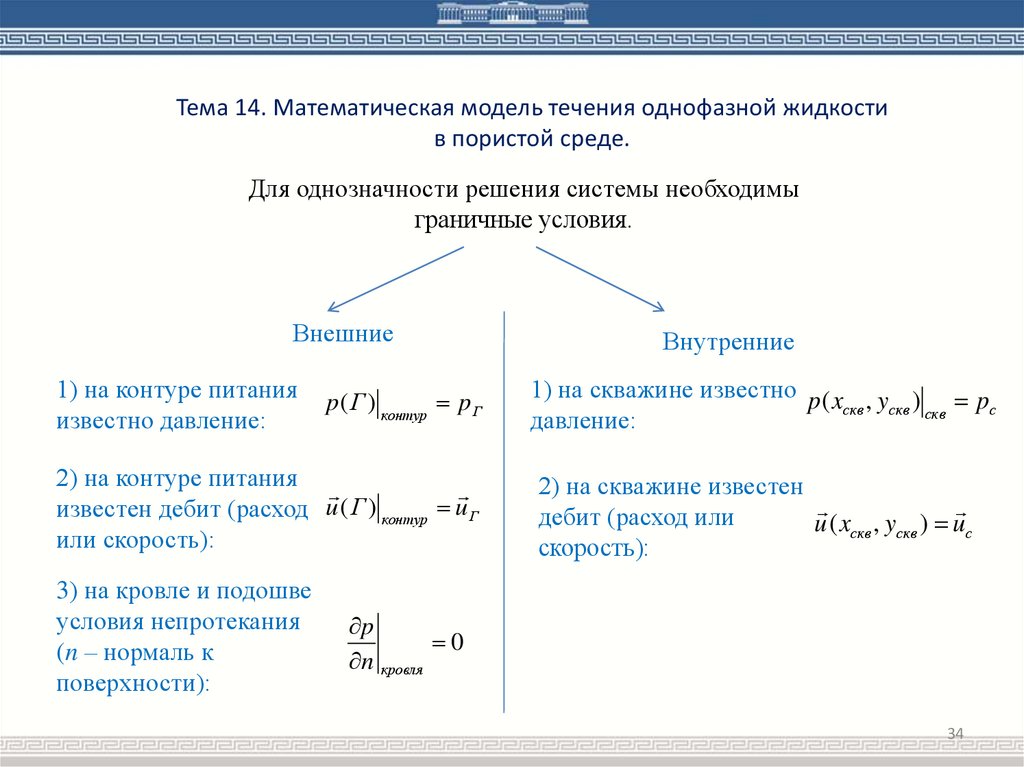
Тема 14. Математическая модель течения однофазной жидкостив пористой среде.
Для однозначности решения системы необходимы
граничные условия.
Внешние
1) на контуре питания
известно давление:
p ( Г ) контур p Г
2) на контуре питания
известен дебит (расход u ( Г ) контур u Г
или скорость):
3) на кровле и подошве
условия непротекания
(n – нормаль к
поверхности):
Внутренние
1) на скважине известно p( x , y ) p
скв
скв скв
с
давление:
2) на скважине известен
дебит (расход или
u ( xскв , yскв ) uс
скорость):
p
0
n кровля
34
35.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Аналитического решения системы (*) в общем случае не
существует!
Для решения системы (*) необходимо:
1) области фильтрации поставить в соответствие сетку;
2) записать систему уравнений (*) для каждого узла сетки;
3) для решения системы уравнений использовать численные
методы.
35
36.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №1. Создание сетки, нумерация узлов.
Для простоты мы будем рассматривать только двухмерный
случай с прямоугольной сеткой. Свойства коллектора и
флюидов известны.
y
Пусть известны:
1) геометрические размеры
области течения:Lx· Ly;
2) количество узлов Nx и Ny.
Lx
Ly
Шаг сетки: hx=Lx/(Nx -1), hy=Ly/(Ny -1)
x
36
37.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
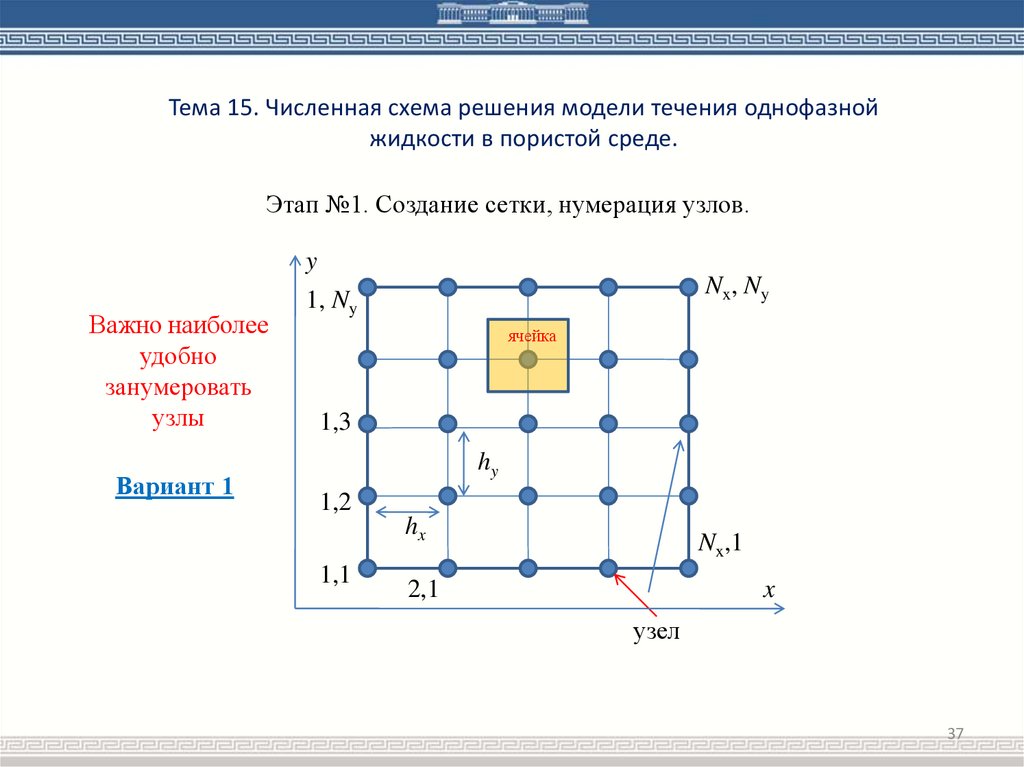
Этап №1. Создание сетки, нумерация узлов.
y
Важно наиболее
удобно
занумеровать
узлы
Вариант 1
Nx, Ny
1, Ny
ячейка
1,3
hy
1,2
hx
1,1
Nx,1
2,1
x
узел
37
38.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №1. Создание сетки, нумерация узлов.
y
Важно наиболее
удобно
занумеровать
узлы
Вариант 2
15
25
5
ячейка
4
3
2
1
7
hx
6
hy
11
узел
Можно придумать свою систему
нумерации, но далее мы будем
использовать именно эту.
x
38
39.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №2. Расположение переменных на сетке, их ассоциация с узлами.
Давление определяется в центре ячейки или узле, а компоненты
скорости в середине ее боковых граней или в полушаге от соседних
узлов
Y
(i,j+1)
uy(i,j+1/2)
(i-1,j) u (i-1/2,j)
x
P(i,j)
ux(i+1/2,j) (i+1,j)
узел
ячейка
uy(i,j-1/2)
(i,j-1)
39
40.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №3. Численная схема решения.
Метод конечных разностей.
1. Распишем уравнение 1) из системы
(*) для узла (i+1/2, j)
и применим метод конечно-разностной
аппроксимации производных
(производная вперед):
**
u x u y u x (i 1 / 2, j ) u x (i 1 / 2, j ) u y (i, j 1 / 2) u y (i, j 1 / 2)
div(u )
0
x
y
hx
hy
Все компоненты скорости в уравнении (**)
ассоциированы с ячейкой для узла (i,j).
40
41.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №3. Численная схема решения.
Метод конечных разностей.
2. Распишем каждую компоненту
скорости в уравнении (**) по
закону Дарси:
u x (i 1 / 2, j )
k {P(i 1, j ) P(i, j )}
k xx P(i, j )
xx
hx
x
u x (i 1 / 2, j )
k {P(i, j ) P(i 1, j )}
k xx P(i, j )
xx
hx
x
***
Снова применим метод
конечно-разностной
аппроксимации производных
(производная вперед)
u y (i, j 1 / 2)
u y (i, j 1 / 2)
k yy P(i, j )
y
k yy P(i, j )
y
k yy {P(i, j 1) P(i, j )}
hy
k yy {P(i, j ) P(i, j 1)}
hy
41
42.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №3. Численная схема решения.
Метод конечных разностей.
3. Подставляем (***) в (**)
k xx {P(i 1, j ) P(i, j )} k xx {P(i, j ) P(i 1, j )} k yy {P(i, j 1) P(i, j )} k yy {P(i, j ) P(i, j 1)}
0
hx2
hx2
hy2
hy2
(0)
k yy
k yy
k yy
k yy
k xx
k xx
k xx
k xx
P
(
i
1
,
j
)
P
(
i
1
,
j
)
P
(
i
,
j
1
)
P
(
i
,
j
1
)
(
) P(i, j ) 0
hx2
hx2
hy2
hy2
hx2 hx2 hy2 hy2
Это рабочее уравнение для узла сетки (i, j)
Замечания:
1) количество уравнений равно количеству узлов сетки;
2) сумма всех коэффициентов при давлениях равна 0. Это следствие
физического смысла уравнения неразрывности – сколько в ячейку
втекает, столько и вытекает.
42
43.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №4. Составление матричного уравнения и его
решение.
Итак, мы получили систему из (Nx·Ny) линейных
алгебраических уравнений (СЛАУ):
k yy
k yy
k yy
k yy
k xx
k xx
k xx
k xx
P
(
i
1
,
j
)
P
(
i
1
,
j
)
P
(
i
,
j
1
)
P
(
i
,
j
1
)
(
) P(i, j ) 0
hx2
hx2
hy2
hy2
hx2 hx2 hy2 hy2
Мы будем решать одним из точных методов – матричным.
43
44.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №4. Составление матричного уравнения и его
решение.
k yy
k yy
k yy
k yy
k xx
k xx
k xx
k xx
P
(
i
1
,
j
)
P
(
i
1
,
j
)
P
(
i
,
j
1
)
P
(
i
,
j
1
)
(
) P(i, j ) 0
hx2
hx2
hy2
hy2
hx2 hx2 hy2 hy2
A P B
A
a11
a12
a13
a14
a15
…
a1,Nx·Ny
a21
a22
a23
a24
a25
…
a2,Nx·Ny
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
aNx·Ny,,Nx·Ny
aNx·Ny,1 aNx·Ny,2 aNx·Ny,3 aNx·Ny,4 aNx·Ny,5
P1
b1
P2
b2
.
.
B
P
.
.
.
.
PN N
bN N
x y
x y
44
45.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №4. Составление матричного уравнения и его
решение.
Для решения матричного уравнения необходимо:
1) найти обратную матрицу A-1 ;
2) умножить обе части уравнения на A-1 слева(!!!), не справа.
1
1
A AP A B
P A 1 B
Решением данного уравнения будет поле давления.
45
46.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №5. Граничные условия.
Рассмотрим условие, при котором на скважине известно
давление Pc. Пусть скважина расположена в узле 5. Значит,
справедливо следующее уравнение:
P 5 = Pc
Как отразить это условие в матричном уравнении?
A
a11
a12
a13
a14
a15 столбец
…
a1,Nx·Ny
5-ый
a21
a22
a23
a24
a25
…
a2,Nx·Ny
…
…
…
…
…
…
…
0
0
0
0
1
…
0
5-ая строчка
aNx·Ny,1 aNx·Ny,2 aNx·Ny,3 aNx·Ny,4 aNx·Ny,5
…
aNx·Ny,,Nx·Ny
0
0
.
B
Pc
.
0
5-ая строчка
46
47.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №5. Граничные условия.
Если на скважине известен дебит, то:
div(u ) q
k yy
k yy
k yy
k yy
k xx
k xx
k xx
k xx
P
(
i
1
,
j
)
P
(
i
1
,
j
)
P
(
i
,
j
1
)
P
(
i
,
j
1
)
(
) P(i, j ) qi , j
hx2
hx2
hy2
hy2
hx2 hx2 hy2 hy2
47
48.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Этап №6. Нахождение компонент скорости.
Неизвестные компоненты скорости находятся на основе
полученного на предыдущем этапе поля давления:
u x (i 1 / 2, j )
k {P (i 1, j ) P (i, j )}
k xx P(i, j )
xx
hx
x
u x (i 1 / 2, j )
k {P (i, j ) P (i 1, j )}
k xx P(i, j )
xx
hx
x
u y (i, j 1 / 2)
u y (i, j 1 / 2)
k yy P(i, j )
y
k yy P(i, j )
y
k yy {P (i, j 1) P (i, j )}
hy
k yy {P (i, j ) P(i, j 1)}
hy
48
49.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Самым трудоемким этапом является составление матрицы А.
Простые правила для проверки:
1) строчка матрицы A соответствует узлу сетки;
2) ненулевые коэффициенты матрицы в данной строке будут расположены в
столбцах, номера которых соответствуют узлам, соседствующим с данным
узлом сетки (за исключением диагональных соседей); остальные
коэффициенты в данной строчке равны нулю;
3) наибольшее по модулю число будет расположено по диагонали матрицы;
4) сумма всех коэффициентов в данной строке (за исключением тех, где есть
скважина) равна нулю.
49
50.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Примеры
1. Девятиточечная система заводнения
Доб. скв.
Доб. скв.
Наг. скв.
Доб. скв.
Поле давления
50
51.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Примеры
2. Добывающая скважина (по центру) с контуром питания
Контур питания
Контур питания
Поле давления
51
52.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
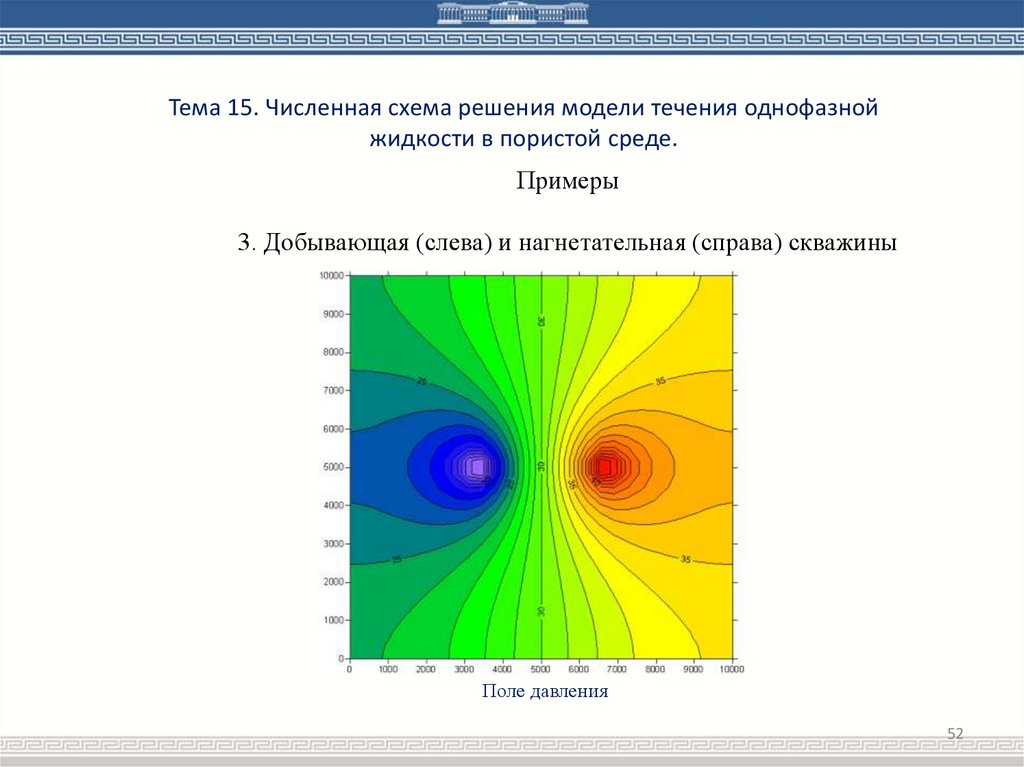
Примеры
3. Добывающая (слева) и нагнетательная (справа) скважины
Поле давления
52
53.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Примеры
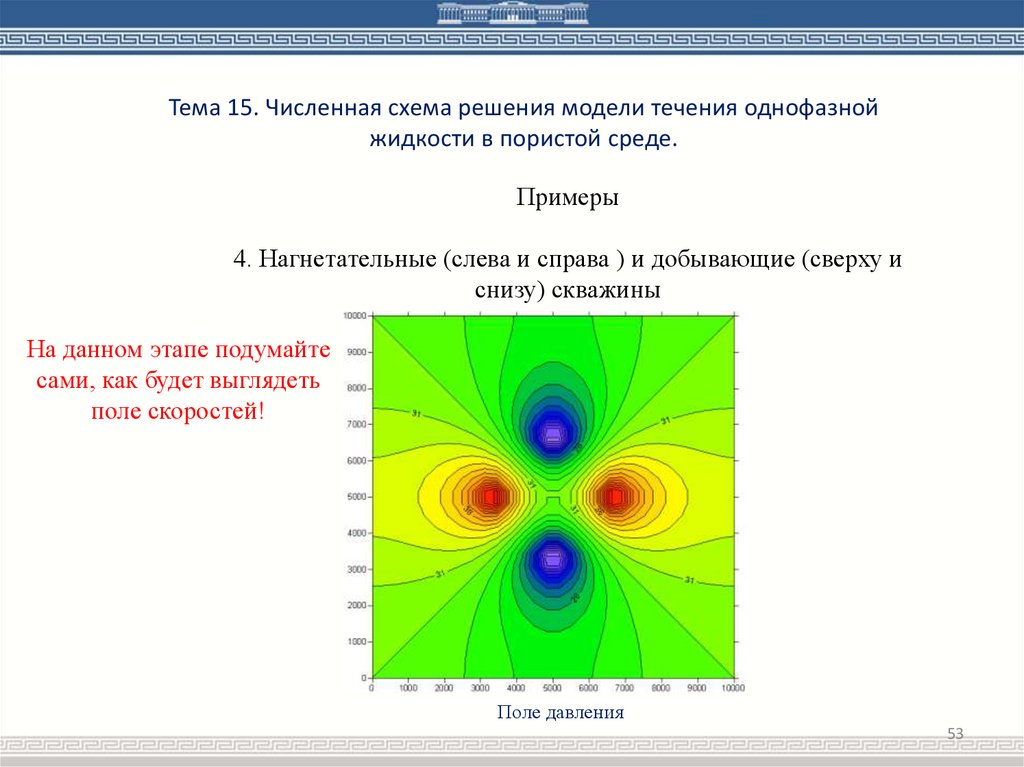
4. Нагнетательные (слева и справа ) и добывающие (сверху и
снизу) скважины
На данном этапе подумайте
сами, как будет выглядеть
поле скоростей!
Поле давления
53
54.
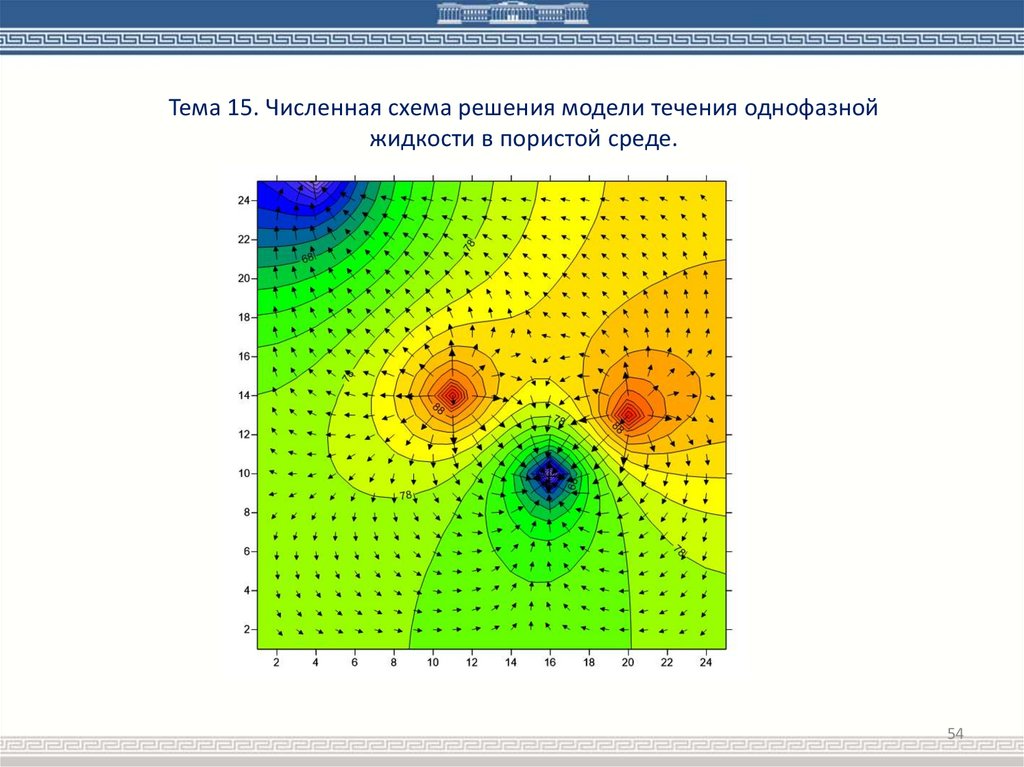
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
54
55.
Тема 15. Численная схема решения модели течения однофазнойжидкости в пористой среде.
Заключительное замечание
k
u gradP
div(u ) 0
с
div(
k
gradP) 0
Если область течения однородна, т.е. коэффициент
проницаемости k является одинаковым в любой точке, то
div( gradP) P 0
Оператор Лапласа
P 0 Это уравнение Лапласа!
55
56.
Спасибо за внимание!56









































 physics
physics








