Трапеция. Средняя линия трапеции. 8 класс

1.

ГОУ ЛНР СГ № 7
Трапеция.
Средняя линия трапеции
Урок геометрии в 8 классе
Учитель:
Ильина Е.И.

2.

На уроке мы узнаем, что такое средняя линия
трапеции, как связана средняя линия трапеции с её
основаниями.
В результате изучения материала учащиеся должны:
знать определения трапеции, равнобедренной и
прямоугольной трапеций, свойство средней линии
трапеции;
уметь применять полученные знания при решении
задач

3.

Вспомним определение параллелограмма:
Параллелограммом называется четырехугольник, у
которого
противоположные
стороны
попарно
параллельны.
Сегодня
познакомимся
с
новым четырёхугольником трапецией

4.

Основание
Основание
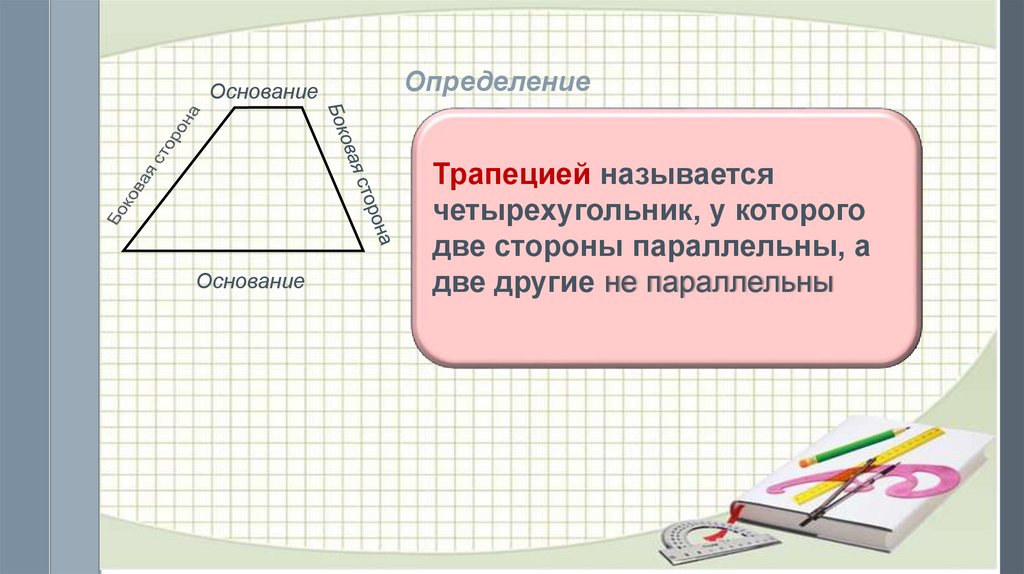
Определение
Трапецией называется
четырехугольник, у которого
две стороны параллельны, а
две другие не
непараллельны
параллельны

5.

Проверим:
В
А
С
1. В четырехугольнике АВСD ВС ∥
АD, АВ ∥ CD
Значит,
АВСD -
трапеция
АD АВ CD ВС -
основание
боковая сторона
боковая сторона
основание
D

6.

2. Какие четырехугольники являются трапециями?
Назовите их основания и боковые стороны
В
С
А
100⁰
В
80⁰
А
F
К
D
D
А1
В
М
C
В1
С

7.

С
В
D
Прямоугольной трапецией
называется трапеция, у которой
одна из боковых сторон
перпендикулярна основаниям
А
ВС ⊥ АВ, ВС ⊥ CD
ВС- высота трапеции

8.

В
С
Равнобедренной трапецией
называется трапеция, у которой
боковые стороны равны
А
D
АВ = СD – боковые стороны

9.

В
K
А
С
Отрезок, соединяющий середины
боковых сторон, называется
средней линией трапеции
L
D
К – середина АВ, L – середина CD
KL – средняя линия трапеции АВCD

10.

Теорема (свойство средней линии трапеции).
Средняя линия трапеции параллельна основаниям и равна
их полусумме
В
K
С
Дано: АВСD – трапеция, АD ⃦ВС,
KL – средняя линия трапеции АВCD
Доказать: KL ∥ ВС, KL ∥ АD,
L
1
KL= (АD + ВС)
2
Доказательство:
А
М
D
1. Дополнительное построение: отрезок ВМ
2. △ВСL = △MDL по стороне и двум прилежащим углам. Из
равенства треугольников следует равенства BL=LM, ВС= MD.
3. KL – средняя линия △АВМ
1
4. Вывод: KL ∥ АD, KL= (АD + ВС)
2

11.

Решаем:
В
K
А
С
N
L
D
1. Основания трапеции равны 7,4 см и 10,6 см.
Чему равна средняя линия трапеции?
2. Средняя линия трапеции равна 8 см, а одно
из оснований
равно 5 см. Чему равно
другое основание?
3. Основания трапеции равны 5 см и 9 см.
Чему равны отрезки, на которые диагональ
трапеции делит ее среднюю линию?

12.

Рефлексия
- Что нового я узнал на уроке?
- Смогу ли я самостоятельно доказать
теорему о свойстве средней линии
трапеции?
- Смогу ли я применять полученные знания?

13.

Домашнее задание:
1. Выучить определения п.45
2. Повторить доказательство теоремы (свойство
средней линии трапеции) по плану, записанному в
тетради
3. Решить №№ 793, 794 (с. 208)