Similar presentations:
Правильные многоугольники
1.
ПРАВИЛЬНЫЕМНОГОУГОЛЬНИКИ
2.
ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИКПравильным многоугольником называется
выпуклый многоугольник, у которого все
углы равны и все стороны равны.
3.
Сумма углов правильного n-угольника(n 2) 180
0
n
(n 2) 180
n
n
0
4.
Вписанная и описанная окружностьОкружность называется вписанной в
многоугольник,
если все стороны многоугольника
касаются этой окружности.
Окружность называется описанной
около многоугольника, если все его
вершины лежат на этой
окружности.
5.
Вписанная и описанная окружностьОкружность, вписанная в
правильный многоугольник,
касается сторон многоугольника
в их серединах.
Центр окружности, описанной
около правильного многоугольника,
совпадает с центром окружности,
вписанной в тот же многоугольник.
6.
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯПлощадь правильного многоугольника
1
S
Pr
2
Сторона правильного многоугольника
180
a n 2 R sin
n
0
Радиус вписанной окружности
180
r R cos
n
0
7.
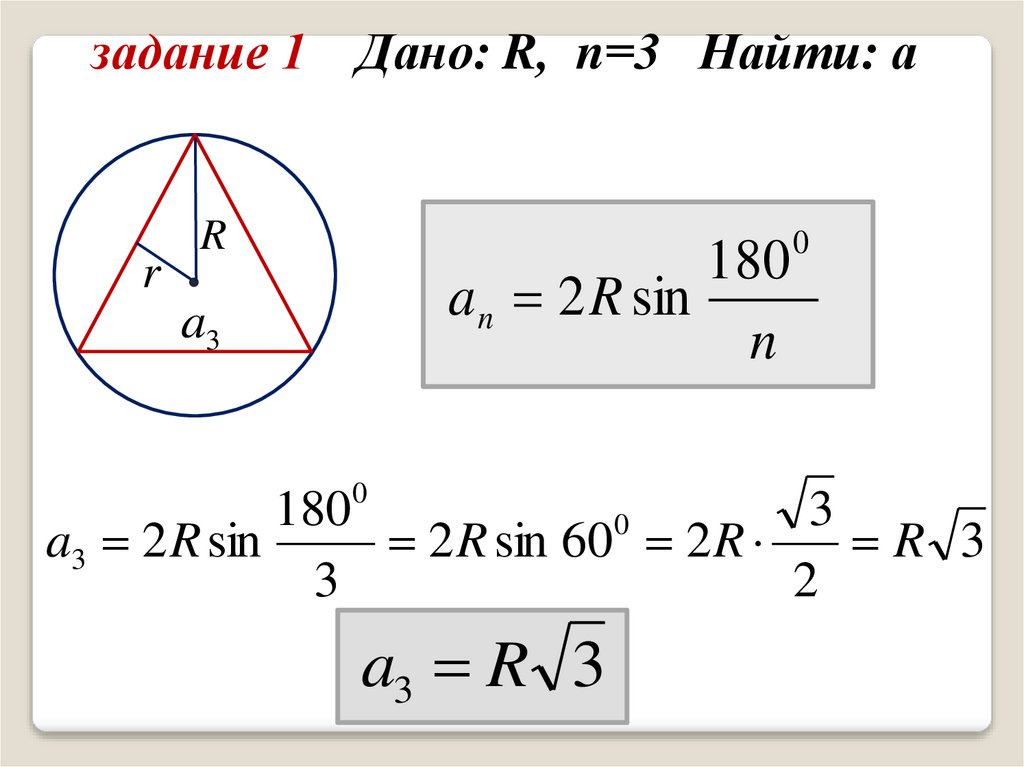
задание 1Дано: R, n=3
Найти: а
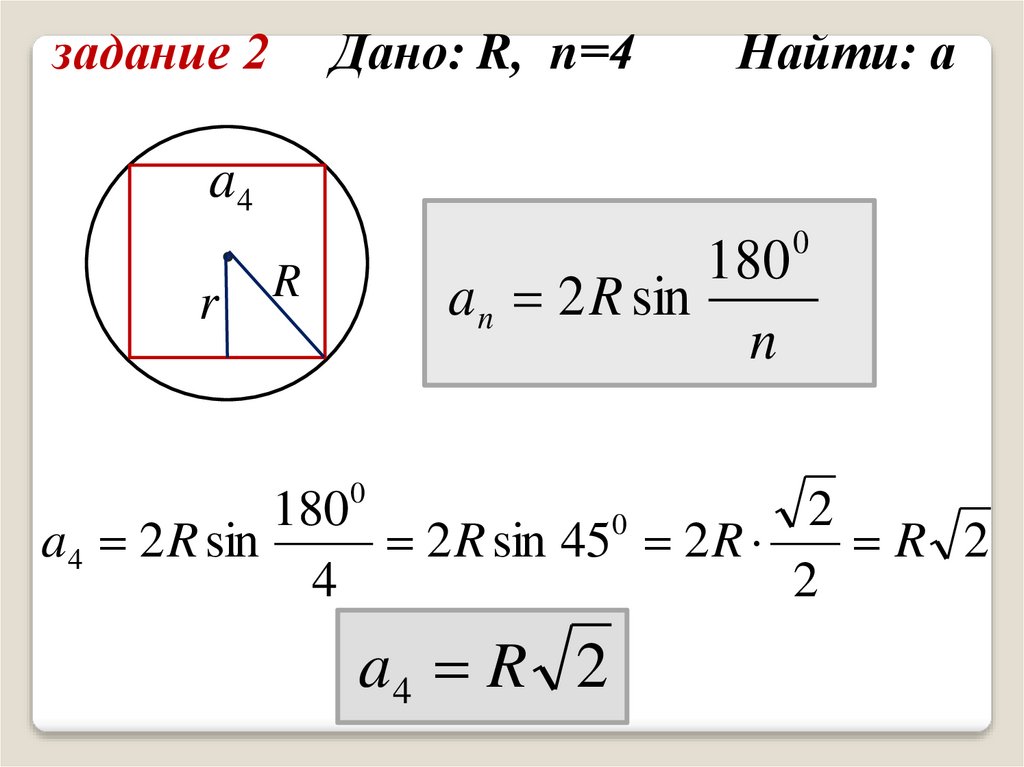
задание 2
Дано: R, n=4
Найти: а
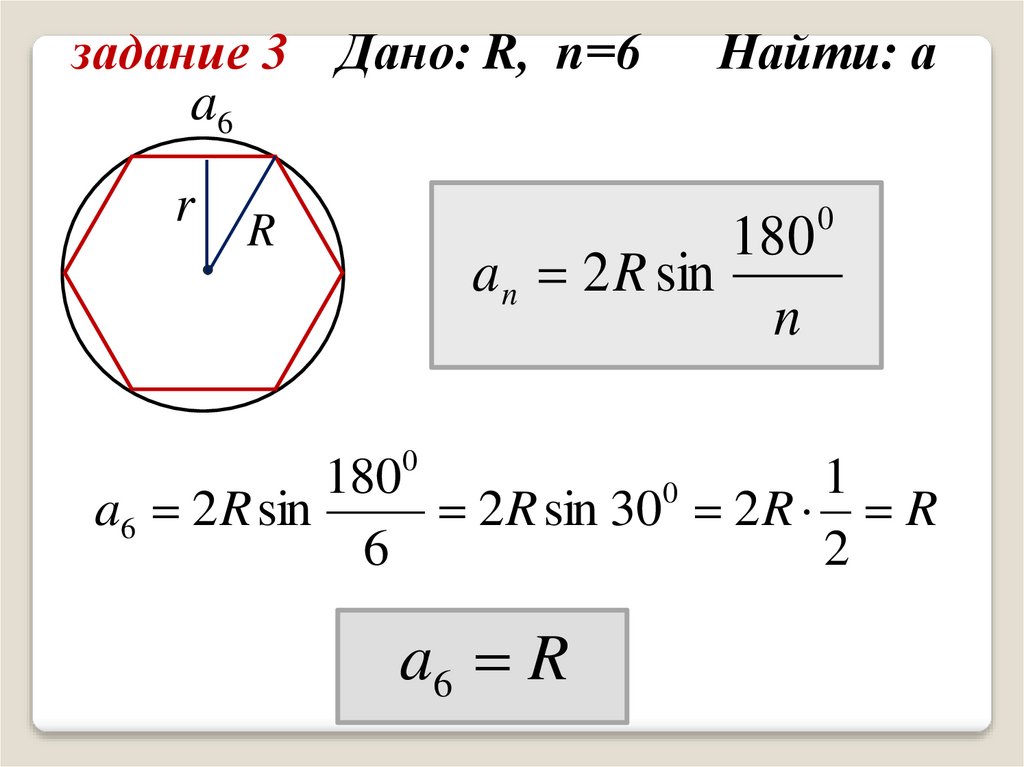
задание 3
Дано: R, n=6
Найти: а
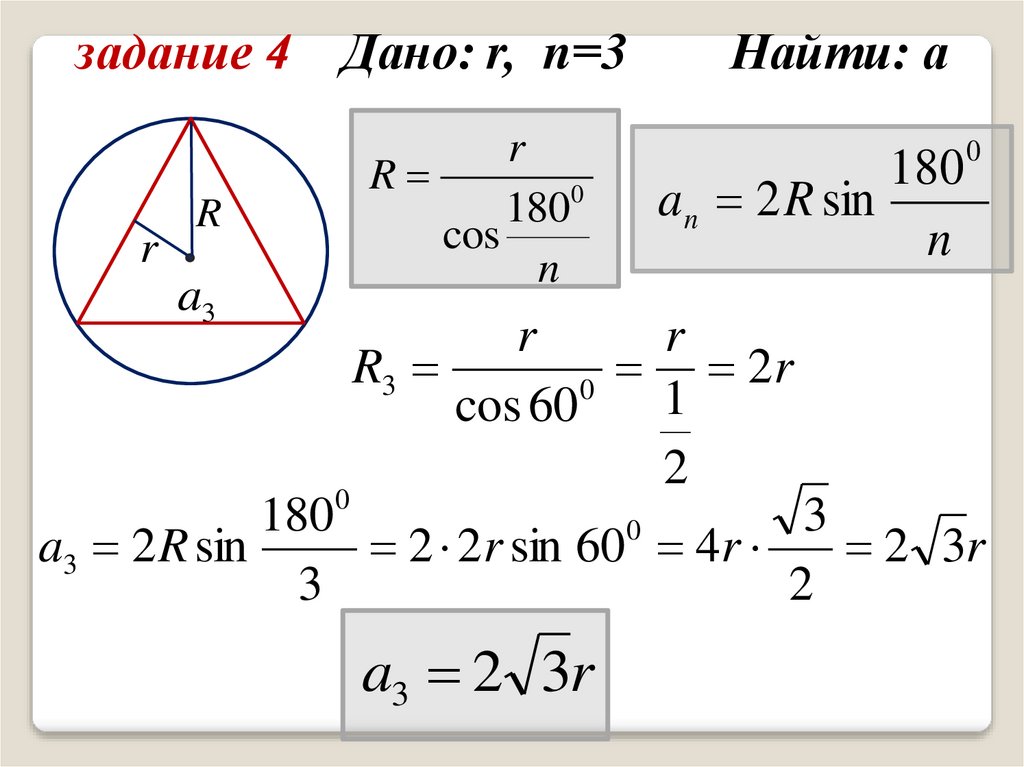
задание 4 Дано: r, n=3
Найти: а
задание 5 Дано: r, n=4
Найти: а
задание 6
Найти: а
Дано: r, n=6
8.
задание 1 Дано: R, n=3 Найти: аr
R
180
a n 2 R sin
n
a3
0
0
180
3
0
a3 2 R sin
2 R sin 60 2 R
R 3
3
2
a3 R 3
9.
задание 2Дано: R, n=4
Найти: а
a4
r
180
a n 2 R sin
n
R
0
0
180
2
0
a4 2 R sin
2 R sin 45 2 R
R 2
4
2
a4 R 2
10.
задание 3 Дано: R, n=6Найти: а
a6
r
R
180
a n 2 R sin
n
0
0
180
1
0
a6 2 R sin
2 R sin 30 2 R R
6
2
a6 R
11.
задание 4 Дано: r, n=3r
r
R
0
180
cos
n
R
a3
0
Найти: а
180
a n 2 R sin
n
0
r
r
R3
2r
0
1
cos 60
2
180
3
0
a3 2 R sin
2 2r sin 60 4r
2 3r
3
2
a3 2 3r
12.
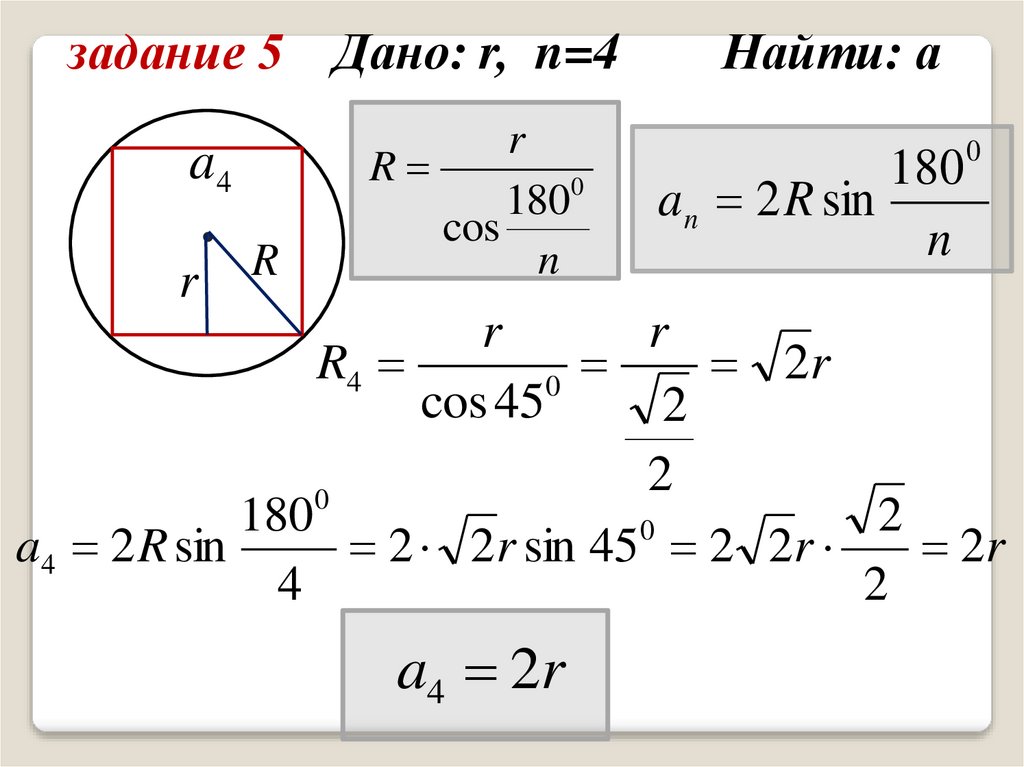
задание 5 Дано: r, n=4a4
r
R
r
R
1800
cos
n
Найти: а
180
a n 2 R sin
n
0
r
r
R4
2r
0
cos 45
2
2
0
180
2
0
a4 2 R sin
2 2r sin 45 2 2r
2r
4
2
a4 2r
13.
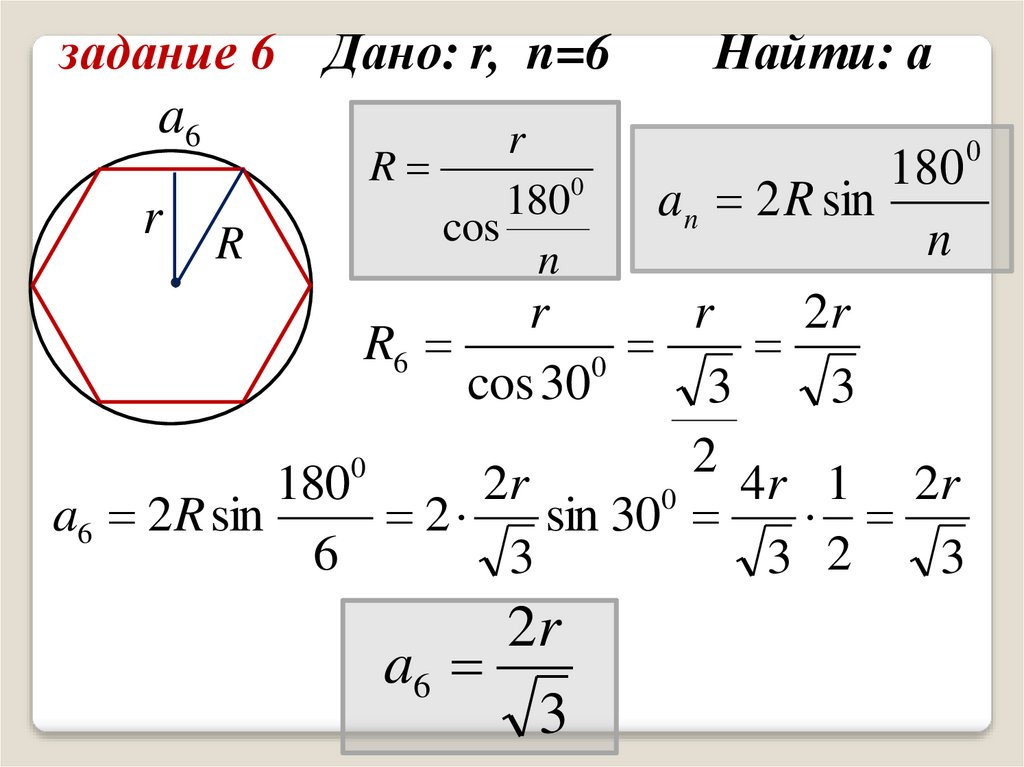
задание 6 Дано: r, n=6a6
r
R
1800
cos
n
Найти: а
180
a n 2 R sin
r R
n
r
r
2r
R6
0
cos 30
3
3
2
0
180
2r
4r 1 2 r
0
a6 2 R sin
2
sin 30
6
3
3 2
3
2r
a6
3
0
14.
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯа3 R 3
a3 2 3r
a4 R 2
a4 2r
a6 R
2r
a6
3
15.
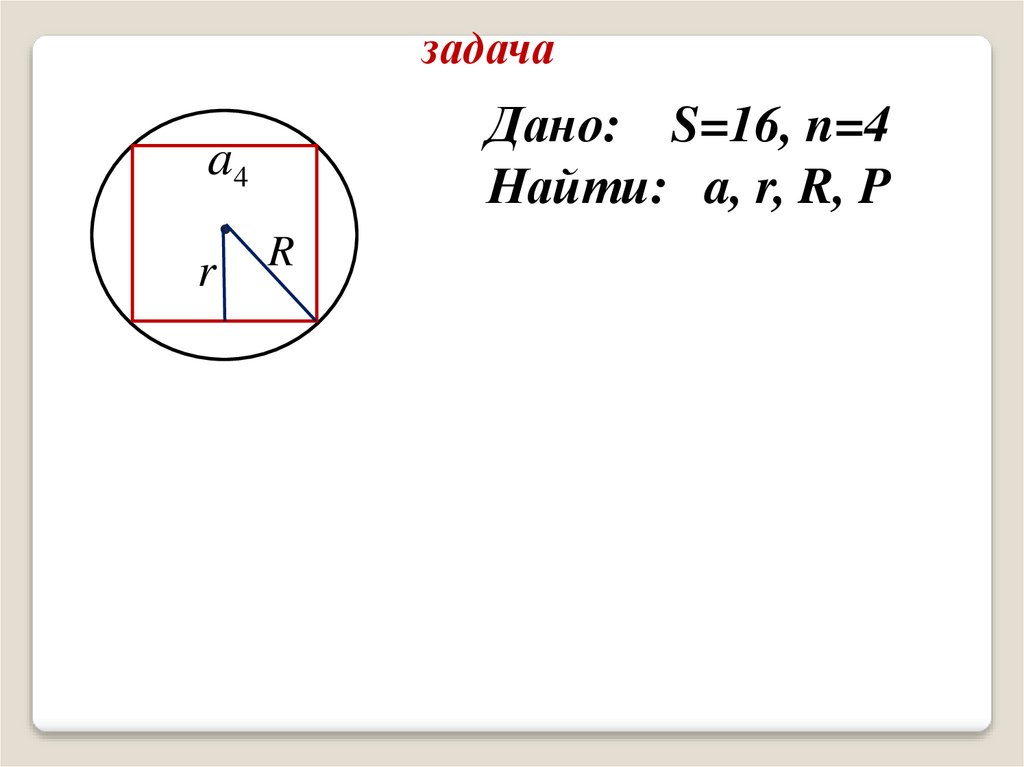
задачаДано: S=16, n=4
Найти: a, r, R, P
a4
r
R








 mathematics
mathematics








