Similar presentations:
Интерференция света. Подготовка к ЕГЭ
1. Подготовка к ЕГЭ
Повторение темыинтерференция света,
11 класс
Рыбицкий В.Л.
учителя физики МБОУ «Лицей №124»
г. Барнаул
2. Теория
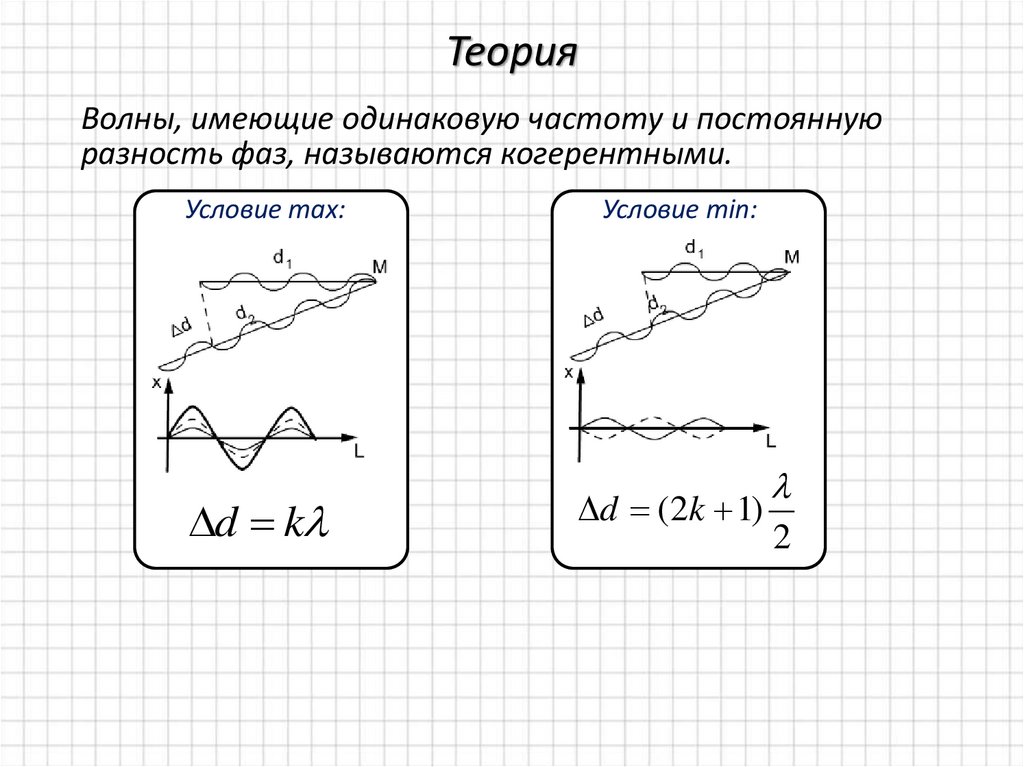
Волны, имеющие одинаковую частоту и постояннуюразность фаз, называются когерентными.
Условие max:
d k
Условие min:
d (2k 1)
2
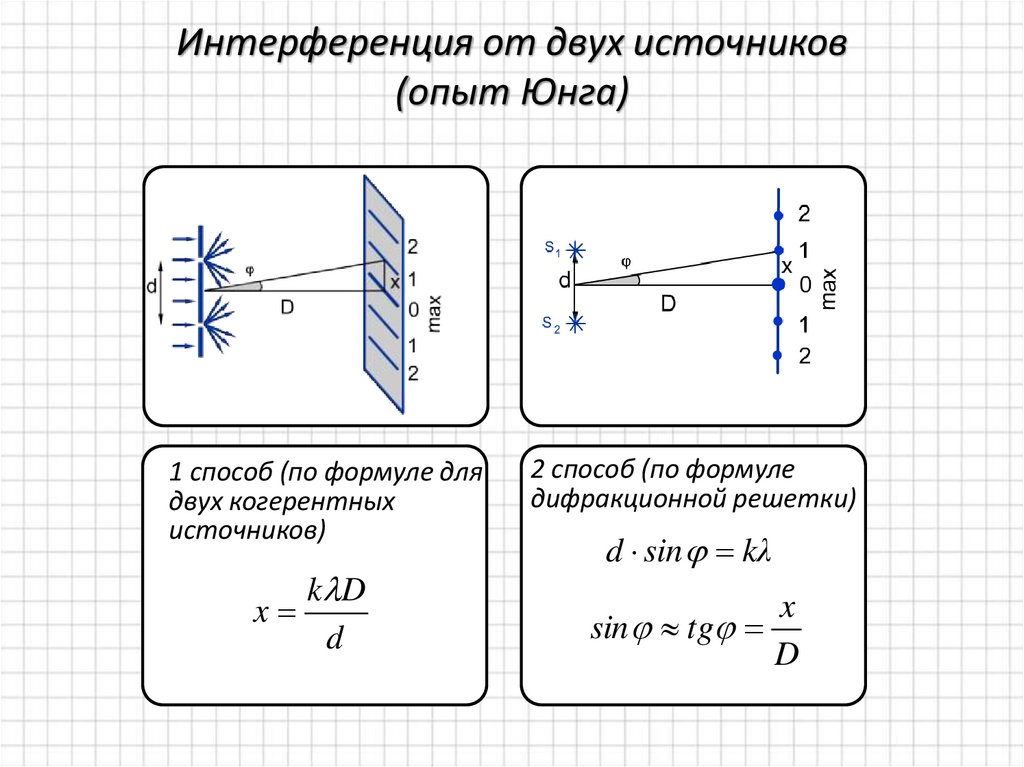
3. Интерференция от двух источников (опыт Юнга)
1 способ (по формуле длядвух когерентных
источников)
k D
x
d
2 способ (по формуле
дифракционной решетки)
d sin kλ
x
sin tg
D
4. Интерференция на тонких пленках
Волны 2, 3 когерентны, т.к. полученыразделением волны 1 при отражении от
поверхностей тонкой пленки.
h
Пленки на поверхности стекла
Воздушные пленки
(в отраженном),
(в проходящем свете)
мыльные пленки (в проходящем)
Условие max:
Условие max:
d 2 h k
d 2h k
Условие min:
d 2h (2k 1)
2
nпленки
Условие min:
d 2h (2k 1)
2nпленки
5.
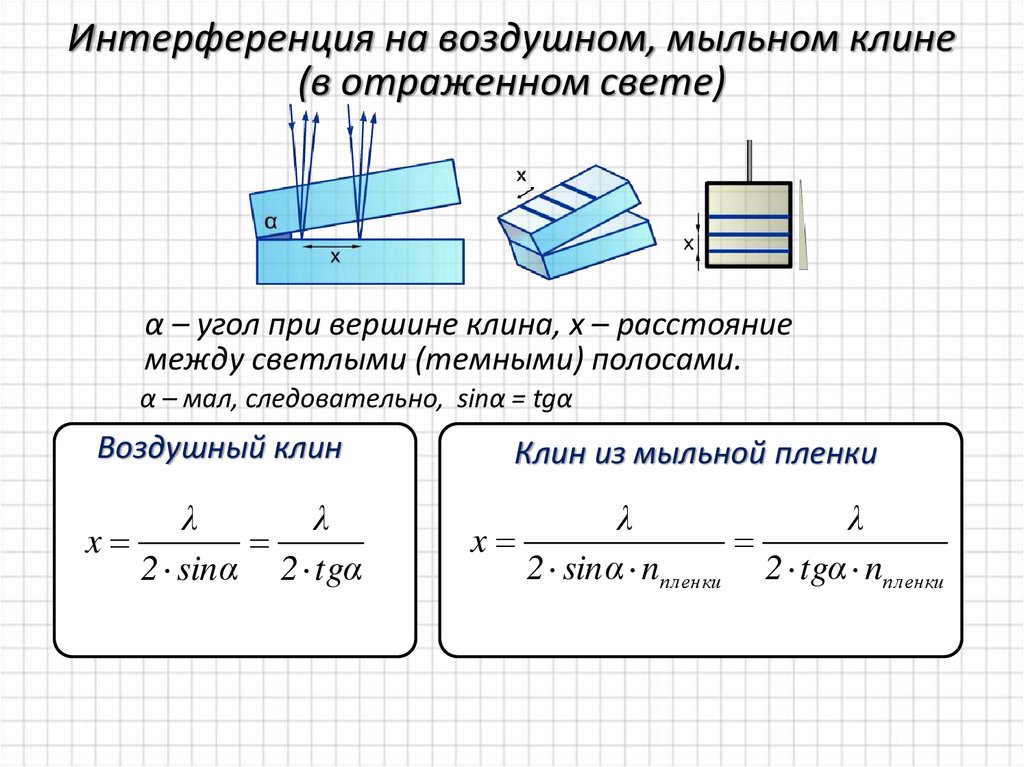
Интерференция на воздушном, мыльном клине(в отраженном свете)
α – угол при вершине клина, x – расстояние
между светлыми (темными) полосами.
α – мал, следовательно, sinα = tgα
Воздушный клин
λ
λ
x
2 sinα 2 tgα
Клин из мыльной пленки
x
λ
λ
2 sinα nпленки 2 tgα nпленки
6.
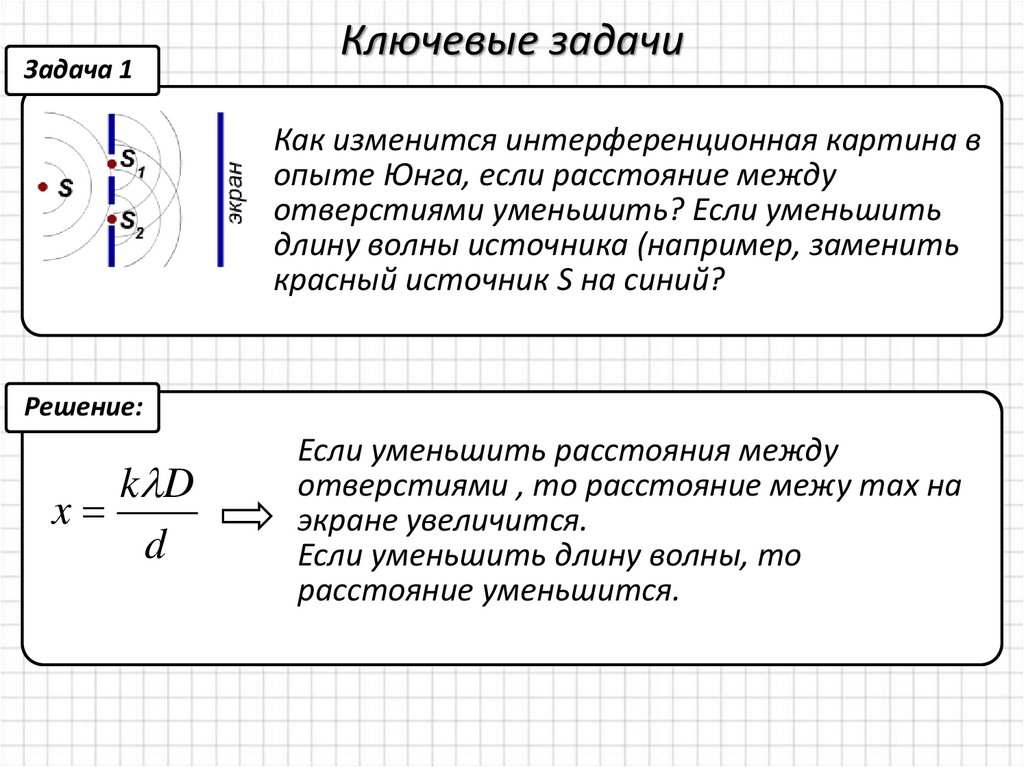
Задача 1Ключевые задачи
Как изменится интерференционная картина в
опыте Юнга, если расстояние между
отверстиями уменьшить? Если уменьшить
длину волны источника (например, заменить
красный источник S на синий?
Решение:
k D
x
d
Если уменьшить расстояния между
отверстиями , то расстояние межу max на
экране увеличится.
Если уменьшить длину волны, то
расстояние уменьшится.
7.
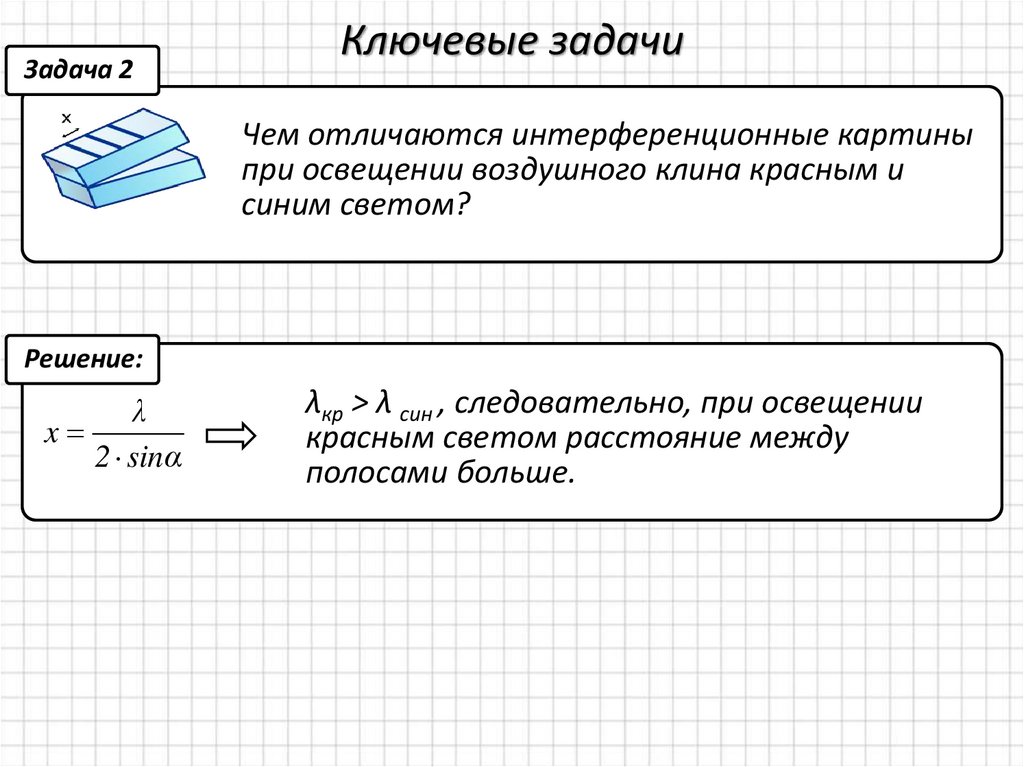
Задача 2Ключевые задачи
Чем отличаются интерференционные картины
при освещении воздушного клина красным и
синим светом?
Решение:
λ
x
2 sinα
λкр > λ син , следовательно, при освещении
красным светом расстояние между
полосами больше.
8.
Задача 3Ключевые задачи
Две когерентные световые волны приходят в точку с
разностью хода 2,25 мкм. Каков результат
интерференции для света с длиной волны 500 нм?
Решение:
6
Δd 2,25 10 м
Δd kλ k
4,5
9
λ
500 10 м
k = 4,5 следовательно, в точке min.
9.
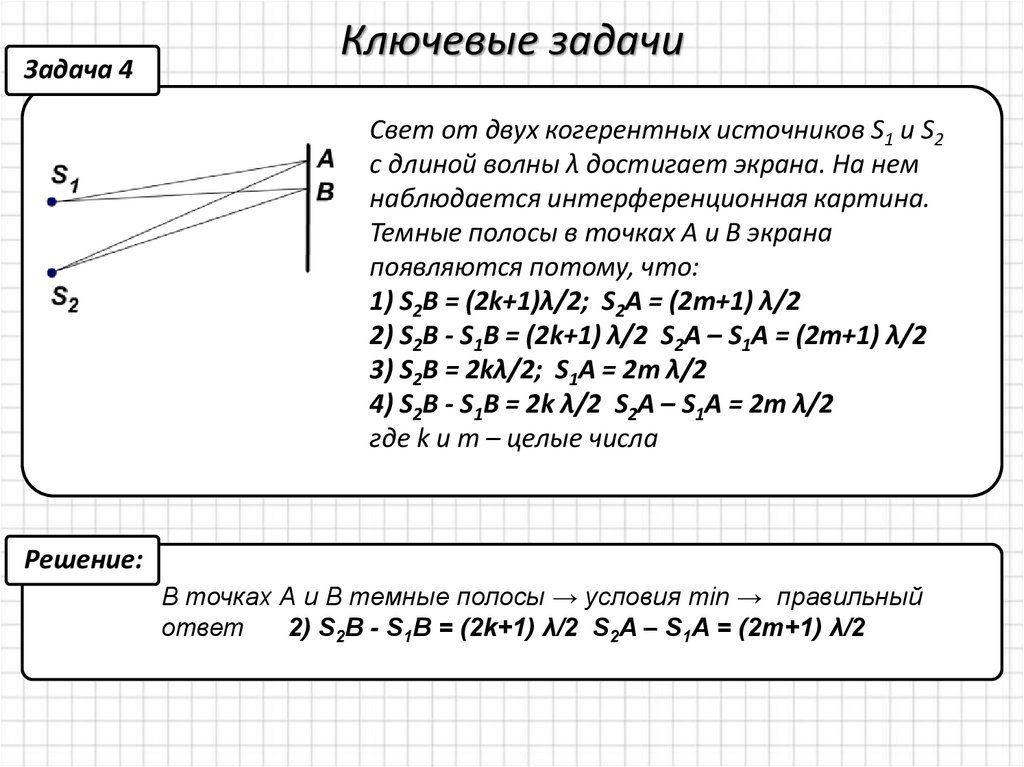
Задача 4Ключевые задачи
Свет от двух когерентных источников S1 и S2
с длиной волны λ достигает экрана. На нем
наблюдается интерференционная картина.
Темные полосы в точках А и В экрана
появляются потому, что:
1) S2B = (2k+1)λ/2; S2A = (2m+1) λ/2
2) S2B - S1B = (2k+1) λ/2 S2A – S1A = (2m+1) λ/2
3) S2B = 2kλ/2; S1A = 2m λ/2
4) S2B - S1B = 2k λ/2 S2A – S1A = 2m λ/2
где k и m – целые числа
Решение:
В точках А и В темные полосы → условия min → правильный
ответ
2) S2B - S1B = (2k+1) λ/2 S2A – S1A = (2m+1) λ/2
10.
Ключевые задачиЗадача 5
На поверхность пластинки из стекла с показателем
преломления 1,70 нанесена тонкая пленка с показателем
преломления 1,50. При какой минимальной толщине
пленки (в «нм») свет с длиной волны 600 нм, падающий
нормально, будет максимально отражаться?
Решение:
1) По условию: nпленки < nстекла и для отраженных
волн выполняется условие max, →
d 2 h k
nпленки
h k
λ
2nпленки
600нм
k
k 200нм
2 1,5
2) Минимальная толщина пленки → k = 1 → h = 200 нм
11.
Задача 6Ключевые задачи
Два полупрозрачных зеркала расположены параллельно
друг другу. На них перпендикулярно плоскости зеркал
падает монохроматический свет. Первый
интерференционный минимум в отраженном свете
наблюдается при расстоянии между зеркалами 150 нм.
Какова длина световой волны (в «нм»)
Решение:
1) Между зеркалами воздушная пленка
2) Первый min в отраженном свете → k = 1
λ λ
d 2h (2k 1)
2 2
3) → λ 4h 4 150нм 600нм
12.
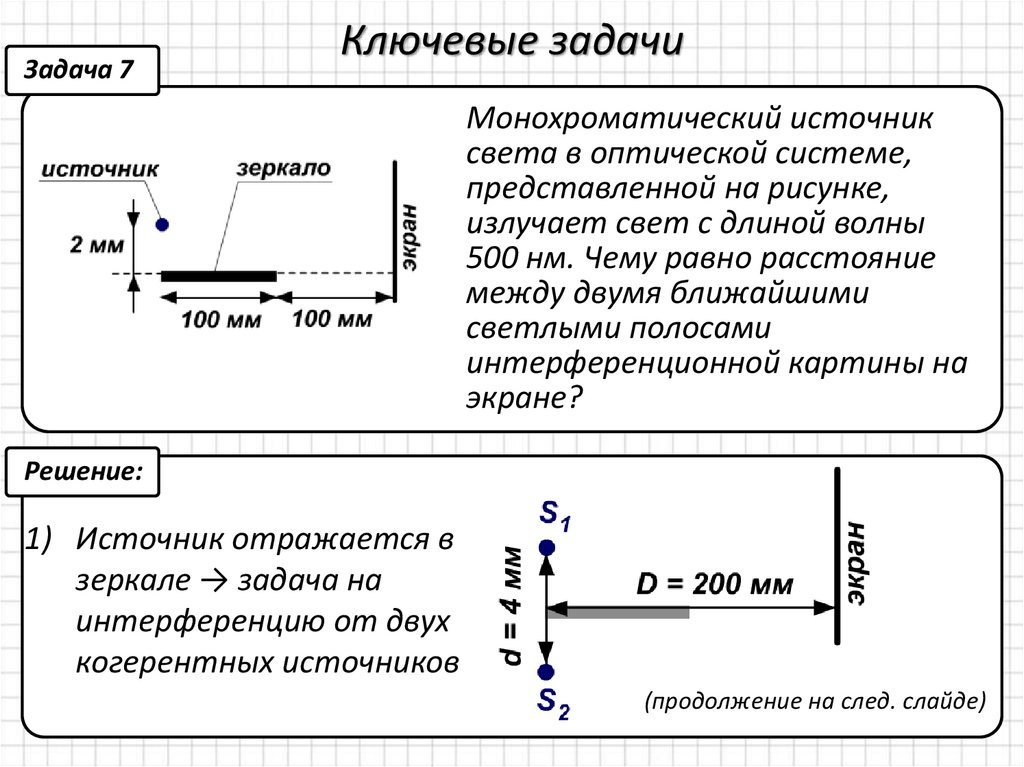
Задача 7Ключевые задачи
Монохроматический источник
света в оптической системе,
представленной на рисунке,
излучает свет с длиной волны
500 нм. Чему равно расстояние
между двумя ближайшими
светлыми полосами
интерференционной картины на
экране?
Решение:
1) Источник отражается в
зеркале → задача на
интерференцию от двух
когерентных источников
(продолжение на след. слайде)
13.
Ключевые задачиРешение:
2) Между max на экране одинаковое
расстояние x, которое находим по
формуле для интерференции от
двух когерентных источников:
k D 1 500 10 9 м 0,2м
5
x
2,5
10
м
3
d
4 10 м
14.
Задача 8Ключевые задачи
Мыльная плёнка образует клин. Пучок
монохроматического света, падая на клин нормально,
создает в проходящем свете интерференционную
картину чередующихся темных и светлых полос. В месте,
где находится первая, считая от ребра клина, темная
полоса, толщина пленки составляет 120 нм. Показатель
преломления мыльной пленки n =4/3 . Определите длину
волны света.
(продолжение на след. слайде)
15.
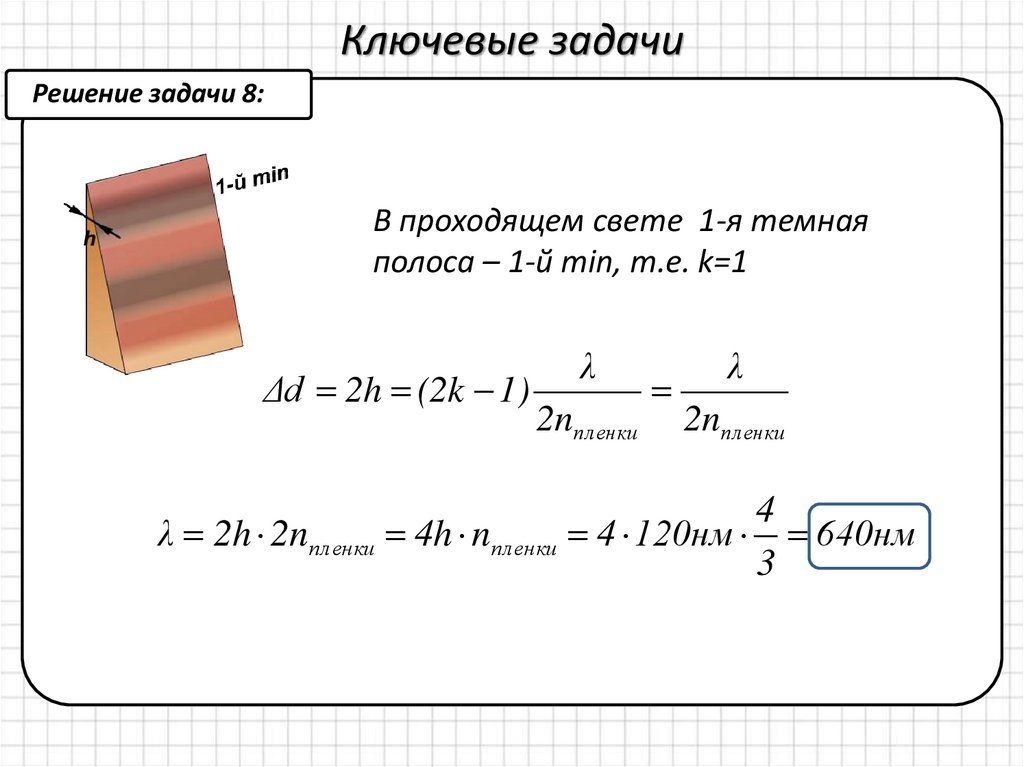
Ключевые задачиРешение задачи 8:
В проходящем свете 1-я темная
полоса – 1-й min, т.е. k=1
Δd 2h (2k 1)
λ
2nпленки
λ
2nпленки
4
λ 2h 2nпл енки 4h nпл енки 4 120нм 640нм
3
16.
Задача 9Ключевые задачи
Мыльная плёнка натянута на
квадратную рамку со стороной d = 2,5 см.
Под действием силы тяжести пленка
приняла форму клина с углом при вершине
α = 2.10-4 рад. Пленка освещается светом
с длиной волны λ = 666 нм (в воздухе).
Сколько светлых полос наблюдается на
пленке в проходящем свете? Показатель
преломления пленки 4/3.
(продолжение на след. слайде)
17.
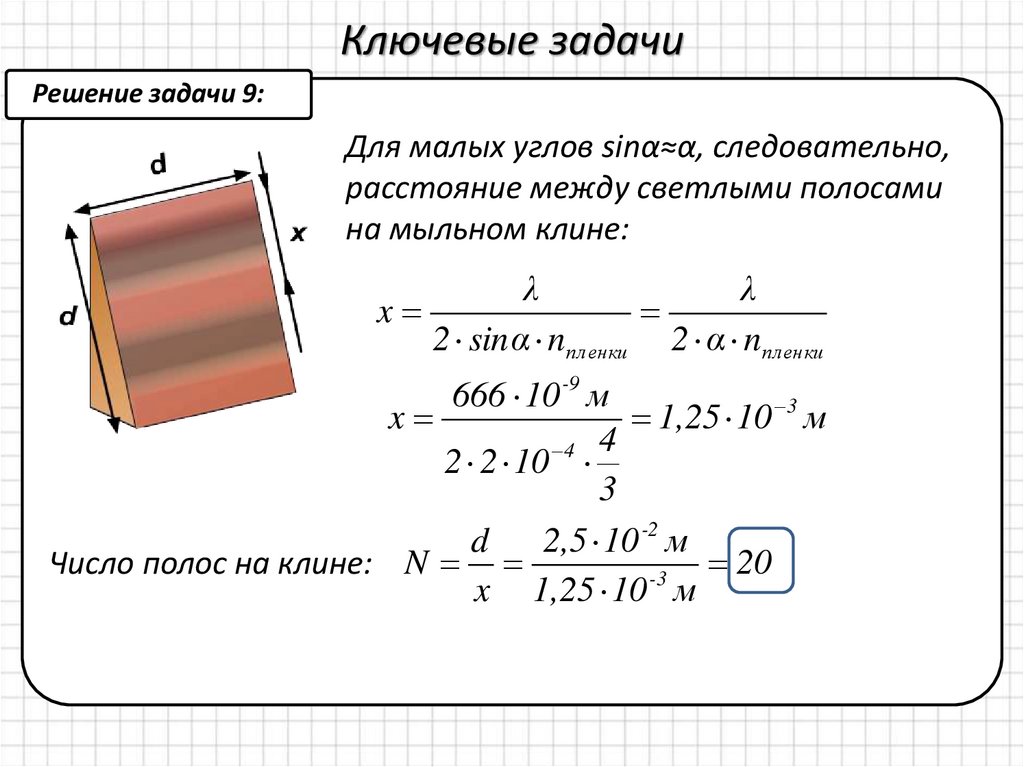
Ключевые задачиРешение задачи 9:
Для малых углов sinα≈α, следовательно,
расстояние между светлыми полосами
на мыльном клине:
λ
λ
x
2 sinα nпленки 2 α nпленки
666 10 -9 м
x
1,25 10 3 м
4 4
2 2 10
3
d
2,5 10 -2 м
Число полос на клине: N
20
-3
x 1,25 10 м








 physics
physics








