Similar presentations:
Кинематика. Решение задач
1.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра строительной физики и химии
Физика
Тема
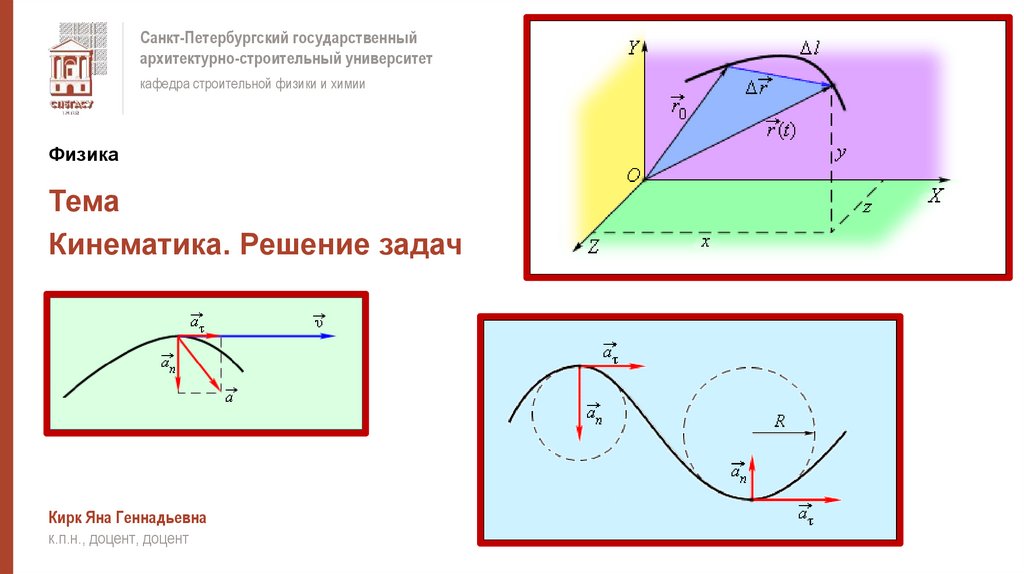
Кинематика. Решение задач
Кирк Яна Геннадьевна
к.п.н., доцент, доцент
2.
3.
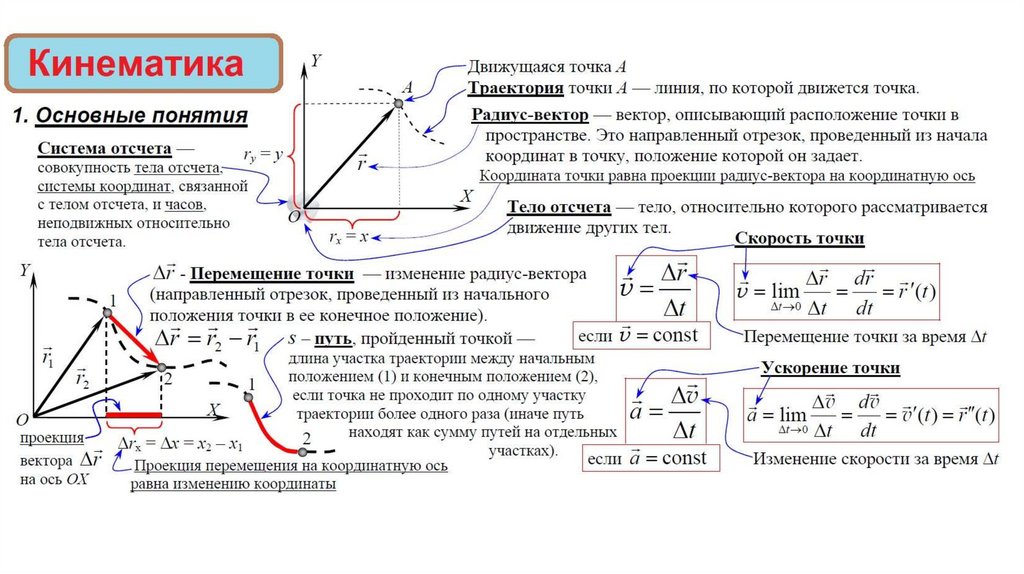
Механическое движение – изменение положения тела относительно других тел с течением времени.Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду
траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).
4.
Относительность движения – различие скорости, направления и траектории движения в различных системахотсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.
5.
6.
7.
8.
9.
1. Тело брошено вертикально вверх с начальной скоростью V0 = 4 м/с. Когда оно достигло верхней точки полетаиз того же начального пункта, с той же начальной скоростью V0 вертикально вверх брошено второе тело. На
каком расстоянии H от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
Дано:
V0 = 4 м/с
Найти:
H=?
Запишем уравнение движения первого тела:
Скорость тела подчиняется уравнению V = V0 – g×t. Когда через время T тело достигает
верхней точки (y=H0), его скорость становится равной V= 0, поэтому 0=V0 –g×T. Откуда
время подъема равно
Тогда высота подъема равна
Когда первое тело начинает падать (при движении вниз) уравнение его движения
принимает вид:
В это же время второе тело начинает подниматься. И его уравнение движения
Когда тела встретились их координаты y1 и y2 стали равными.
10.
То есть y1=y2, откудаИз этого уравнения находим время, через которое тела встретятся:
Нам уже известно, что ,
Поэтому
Высоту найдем подстановкой этого времени t в уравнение
То есть
Подставляем числа
11.
2. Тело брошено под углом α=30° к горизонту со скоростью V0 = 30м/с. Каковы будут нормальное аn итангенциальное аτ ускорения тела через время t=1с после начала движения?
Дано:
V0=30 м/с
α=30°
t=1с
Найти:
1) an = ?
2) aτ = ?
Проекции начальной скорости на оси X и Y равны соответственно
Уравнение изменения скорости со временем записывается в виде
Через время t1 тело находится на максимальной высоте Vy=0. Поэтому
Откуда время подъема равно
Момент времени t=1c меньше t1. Поэтому на этапе t=1c происходит еще подъем. При подъеме скорость тела вдоль оси
X не изменяется (постоянна) и равна
Скорость же вдоль оси Y изменяется со временем по закону
12.
Из рисунка видно, чтопоэтому
Поэтому искомые ускорения равны (см. рис.)
Аналогично находим:
13.
3. Материальная точка движется по окружности с постоянной угловой скоростью ω=π/6 рад/с. Во сколько разпуть ΔS, пройденный точкой за время T=4 с, будет больше модуля ее перемещения Δr-? Принять, что в момент
начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного
положения был повернут на угол φ0 = π/3рад.
Дано:
ω=π/6 рад/с
T=4 с
Зависимость угла поворота от времени записывается в
виде:
Тогда через время T=4c точка повернется на угол
φ0 = π/3рад
Найти:
ΔS/Δr = ?
Из рисунка видно, что пройденный путь равен
ΔS=Δφ×R.
Перемещение найдем из треугольника (см. рис.).
Поэтому
14.
Тогда искомое отношение равноПодставляем числа
15.
4. Материальная точка движется в плоскости ху согласно уравнениям х=A1+B1t+C1t2 и y=A2+B2t+C2t2, гдеB1=7 м/с, С1=– 2м/с2, B2= – 1м/с, С2 =0,2 м/с2. Найти модули скорости и ускорения точки в момент времени t = 5с.
Дано:
х=A1+B1t+C1t2
Запишем радиус-вектор. Он равен , где i – орт оси X, а j – орт оси Y. Поэтому получаем
y=A2+B2t+C2t2
B1=7 м/с
С1=– 2м/с2
B2= – 1м/с
С2 =0,2 м/с2
t = 5с
Найти:
V(t) = ?
a(t) = ?
Скорость есть производная перемещения по времени. Поэтому
Эта величина является вектором. Проекция скорости V на ось X равна
Vx=B1+2C1t,
на ось Y равна
Vy= B2+2C2t.
Тогда модуль скорости равен
Подставляем числа.
16.
По определению ускорение это производная скорости по времени. ПоэтомуПроекция ускорения a на ось X равна ax=2C1, на ось Y равна ay= 2C2.
Поэтому
Подставляем числа.
17.
5. По краю равномерно вращающейся с угловой скоростью ω=1 рад/с платформы идет человек и обходитплатформу за время t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли?
Принять радиус платформы R = 2м.
Дано:
ω=1 рад/с
По определению центростремительное ускорение равно
Так как человек обходит платформу по краю, то его скорость относительно платформы равна
t = 9,9 с
R = 2м
Найти:
Если человек обходит платформу по направлению вращения, скорость человека относительно
земли будет максимальна:
V=V1+V2.
a=?
Где V2=ω×R – скорость вращения края платформы. Поэтому
Подставляем
Подставляем числа
18.
6. Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением ε. Определитьтангенциальное ускорение аτ точки, если известно, что за время T = 4 с она совершила три оборота и в конце
третьего оборота ее нормальное ускорение аn=2,7 м/с2.
Дано:
R = 30 см
aτ = const
T= 4 с
N(T) = 3
аn=2,7 м/с2
Найти:
aτ = ?
На рисунке показаны направления тангенциального aτ, нормального an ускорений и полного
ускорений точки.
По определению нормальное ускорение
, где ω – угловая скорость точки, R - радиус.
Откуда
Угловая скорость с другой стороны равна ω=ω0+εt. Откуда
По определению тангенциальное ускорение
Зависимость угла поворота от времени:
Поэтому число оборотов равно
Подставляем сюда
и получаем
, где ε – угловое ускорение точки.
19.
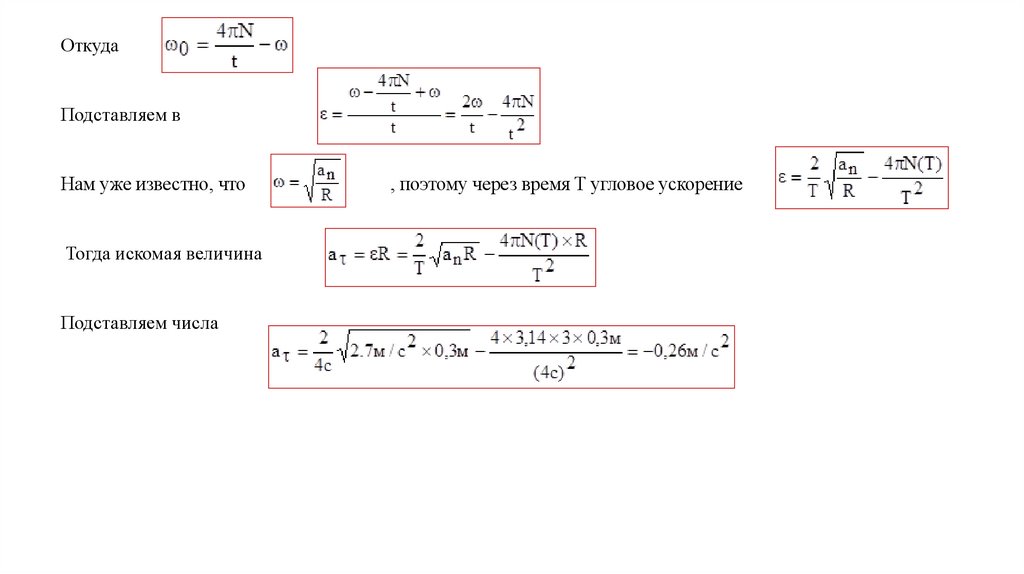
ОткудаПодставляем в
Нам уже известно, что
Тогда искомая величина
Подставляем числа
, поэтому через время T угловое ускорение
20.
Кинематика1. Частица массой m = 2 кг движется со скоростью
V a t 2 i b t 2 j c k (м/с).
Найти:
а) модуль перемещения r частицы за первые 2 секунды ее движения,
б) модуль скорости v в момент t = 2 с,
в) приближенное значение пути S, пройденного частицей за 12-ю секунду
движения,
г) модуль результирующей всех сил, действующих на частицу в момент t = 2
с.
ВАРИАНТ 1
a = 3, b = 2, c = 1.
ВАРИАНТ 2
a = 5, b = 2, c = 4.
ВАРИАНТ 3
a = 3, b = 1, c = 2.
ВАРИАНТ 4
a = 4, b = 3, c = 1.
ВАРИАНТ 5
a = 3, b = 5, c = 2.
ВАРИАНТ 6
a = 4, b = 4, c = 2.
ВАРИАНТ 7
a = 4, b = 5, c = 1.
ВАРИАНТ 8
a = 2, b = 3, c = 2.
ВАРИАНТ 9
a = 4, b = 3, c = 2.
ВАРИАНТ 10
a = 3, b = 3, c = 2.
21.
2. Небольшое тело (материальнаяточка) брошено из точки О под
углом α к горизонту с начальной
скоростью v0 (рис.). Пренебрегая
сопротивлением воздуха, найти:
а) время полета τ,
б) дальность полета L,
в) наибольшую высоту поднятия
тела h,
г) радиус кривизны R траектории в точке О, наивысшей точке подъема тела и
в момент времени t1.
Точки бросания и падения считать лежащими на одном уровне.
ВАРИАНТ 1
v0 = 20 м/с, α = 450, t1 = 2 с.
ВАРИАНТ 2
v0 = 45 м/с, α = 300, t1 = 3 с.
ВАРИАНТ 3
v0 = 30 м/с, α = 600, t1 = 1,5 с.
ВАРИАНТ 4
v0 = 30 м/с, α = 450, t1 = 2 с.
ВАРИАНТ 5
v0 = 25 м/с, α = 350, t1 = 2 с.
ВАРИАНТ 6
v0 = 35 м/с, α = 400, t1 = 3,5 с.
ВАРИАНТ 7
v0 = 30 м/с, α = 500, t1 = 2,5 с.
ВАРИАНТ 8
v0 = 15 м/с, α = 450, t1 = 1 с.
ВАРИАНТ 9
v0 = 30 м/с, α = 250, t1 = 1,5 с.
ВАРИАНТ 10
v0 = 40 м/с, α = 350, t1 = 3 с.
22.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра строительной физики и химии
Авторы:
Кирк Яна Геннадьевна
sfh@spbgasu.ru

















 physics
physics








