Similar presentations:
Временные характеристики линейных стационарных автоматических систем
1.
Автоматика и управлениеТема 3. Временные
характеристики линейных
стационарных автоматических
систем
ПЗ 4. Аналитическое вычисление весовой и
переходной функций.
2.
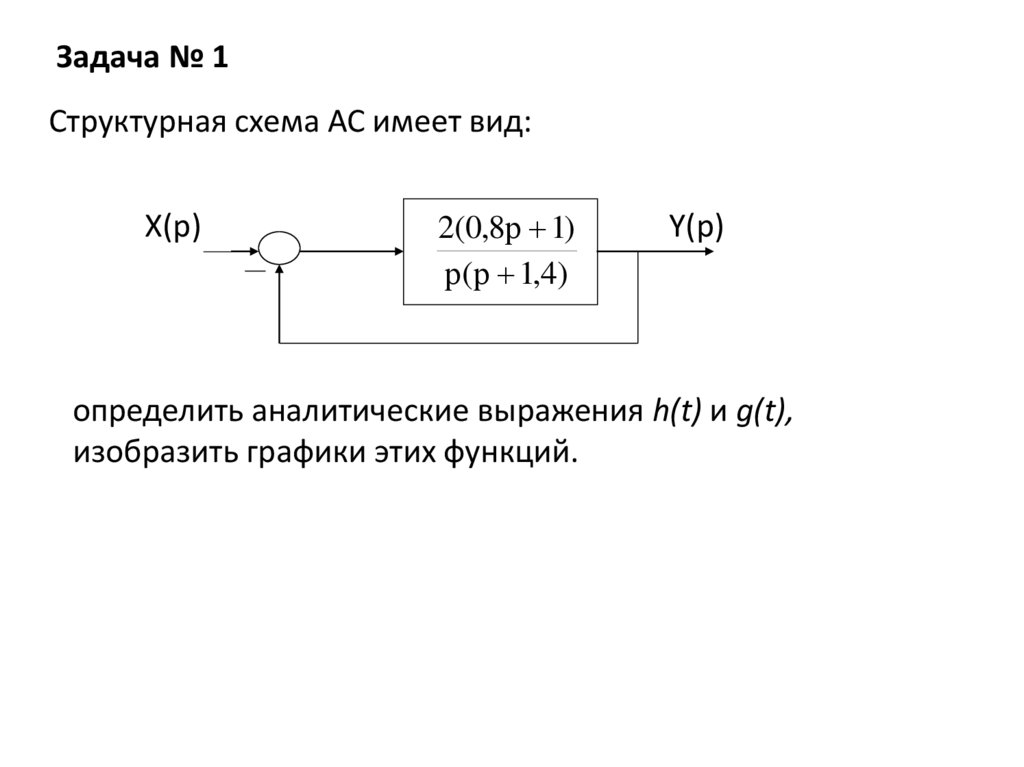
Задача № 1Структурная схема АС имеет вид:
X(p)
2(0,8р 1)
р(р 1,4)
Y(p)
определить аналитические выражения h(t) и g(t),
изобразить графики этих функций.
3.
X(p)1,6 p 2
H( p )
;
2
p( p 3 p 2 )
2(0,8р 1)
р(р 1,4)
G( p )
Y(p)
1,6 p 2
p2 3 p 2
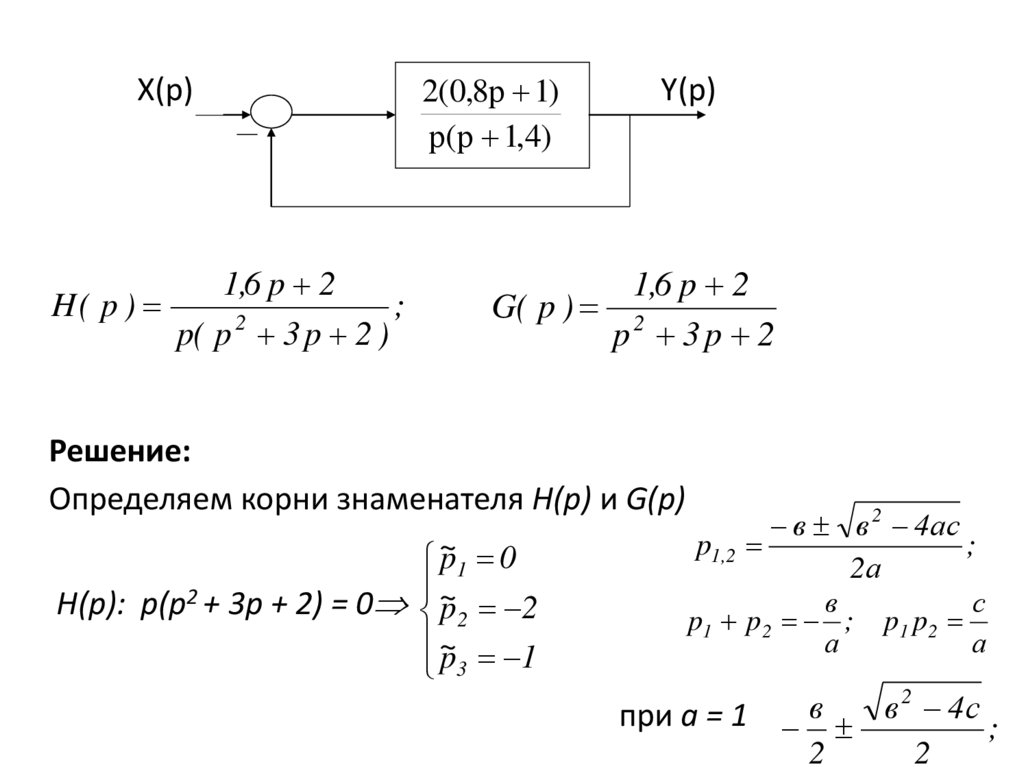
Решение:
Определяем корни знаменателя Н(р) и G(p)
в в 2 4 ас
p1,2
;
~p1 0
2а
в
с
H(p): p(p2 + 3p + 2) = 0 ~p2 2
p1 p2 ; p1 p2
а
а
~p 1
3
2
в
в
4с
при а = 1
;
2
2
4.
G(p): p2 + 3p + 2 = 0p1 2
p 2 1
в
в 2 4с
;
2
2
Определяем коэффициент С0, Сi разложения функций h(t) и g(t)
g (t ) C (t ) n C e p t , t 0;
0
i
i 1
bn
C
Ф( ), m n
0
a
n
C0 0,
m n
i
Ci
A’(p) : (p2+3p+2)’= 2p+3
g (t ) : С1
Определяем оригинал
С2
2 t
t
1
,
2
e
0
,
4
e
g(t) =
B( p )
A(1) ( p) p pi
1,6 p 2
1,2
1,2;
p 2
2p 3
1
1
1,6 p 2
0,4
0,4
p 1
2p 3
1
2
5.
1,6 p 2n
Ф
(
p
)
~
~
p2 3 p 2
h(t ) C0 1 t Ci e Pit , t 0;
i 1
~ b0
1,6 p 2
H( p )
;
C0 Ф(0),
2
а0
p( p 3 p 2 )
~
В( pi )
2
2
С
.
p
(
p
3
p
2
)
'
3
p
6 p 2
[pA(p)]’:
i
'
[ pi A( pi )]
~p1 0
~
p2 2
~p 1
3
~ 2
h(t ) : С0 1
2
~
С1
1,6 p 2
1,2
0,6;
~
p 2 2
2
3p 6 p 2
2
~
С2
h(t) = 1
1,6 p 2
0,4
0,4;
~
p 3 1
2
3p 6 p 2
1
( 0,6)e 2t ( 0,4)e t 1 0,6e 2t 0,4e t
6.
Проверка:g(t) = h(1)(t)
g(t) = ( 1 0 ,6 e
2 t
0 ,4e t )' 1,2e 2t 0 ,4e t
Проверить h(0) и g(0); h( ) и g( )
7.
Задача № 2На вход системы
X(p)
1
р
действует входной сигнал
Y(p)
x(t) = 2 (t – 1) - 3 (t – 2) + 4 (t – 4)
Изобразить график выходного сигнала.
Если на вход системы действует –импульс, то выход системы
есть весовая функция g(t). Если на вход ЛС АС действует
комбинация –импульсов, сдвинутых по времени, то в силу
линейности системы её выход будет также линейная
комбинация весовых функций с соответствующим сдвигом.
выходной сигнал системы
Весовая функция системы
(интегрирующего звена)
y(t) = 2g(t-1) – 3g(t – 2) + 4g(t – 4)
1 1
g( t ) L G( p ) L W ( p ) L 1( t ),
p
1
1
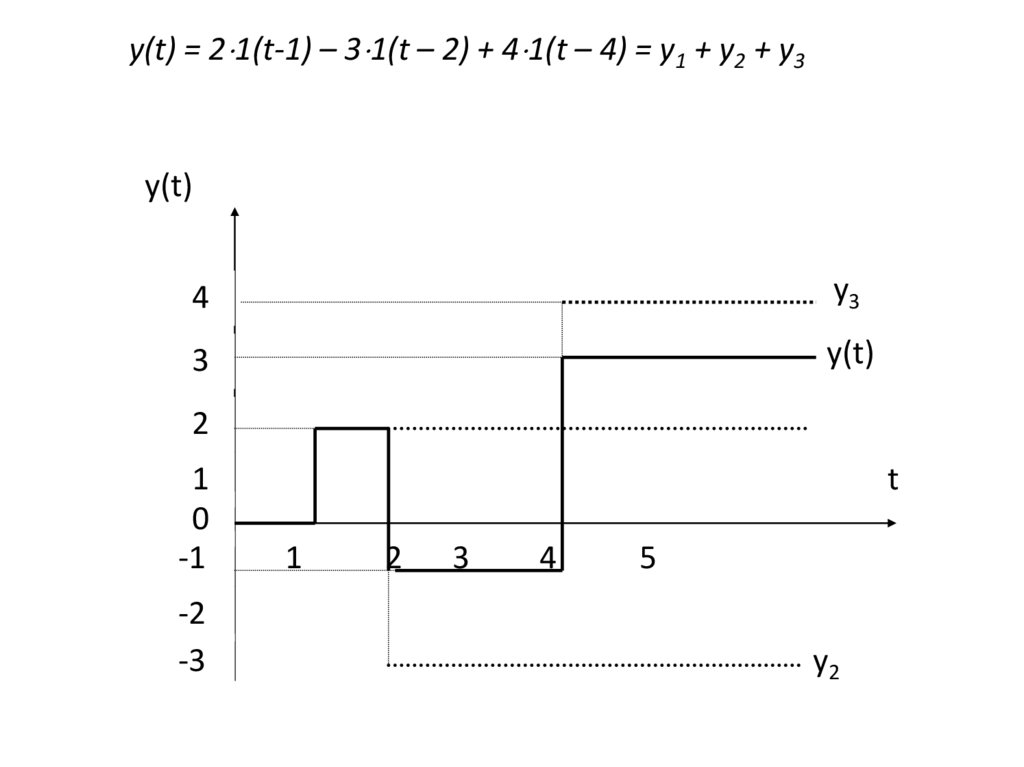
y(t) = 2 1(t-1) – 3 1(t – 2) + 4 1(t – 4) = y1 + y2 + y3
8.
y(t) = 2 1(t-1) – 3 1(t – 2) + 4 1(t – 4) = y1 + y2 + y3y(t)
4
y3
3
y(t)
2
1
0
-1
-2
-3
t
1
2
3
4
5
y2
9.
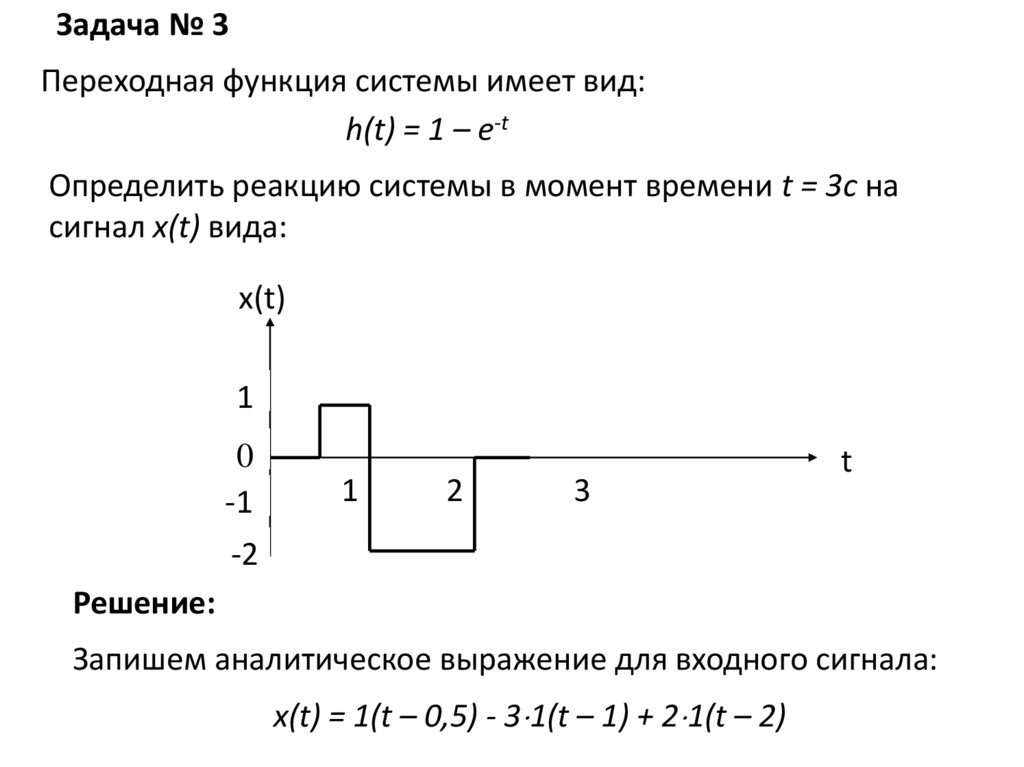
Задача № 3Переходная функция системы имеет вид:
h(t) = 1 – e-t
Определить реакцию системы в момент времени t = 3с на
сигнал x(t) вида:
x(t)
1
0
-1
1
2
3
t
-2
Решение:
Запишем аналитическое выражение для входного сигнала:
x(t) = 1(t – 0,5) - 3 1(t – 1) + 2 1(t – 2)
10.
x(t) = 1(t – 0,5) - 3 1(t – 1) + 2 1(t – 2)h(t) = 1 – e-t
Если вход системы есть единичная ступенчатая функция, то ,
по определению, выход – переходная функция.
y(t) = h(t – 0,5) – 3h(t – 1) + 2h(t – 2) =1 – e-(t-0,5)- 3 + 3 e-(t-1)+ 2 - 2 e-(t-2)=
= 3 e-(t-1)- 2 e-(t-2)- e-(t-0,5)
y(3) = 3 e-2- 2e-1- e-2,5.
11.
12( p 1) 2
H ( p ) Ф( р )
p
p( p 3)3
2
1 2
(
1
)
2
p 2( p 1)
p
p
h(0) lim p H ( p) lim
0
lim
3
3
p
p
p
p( p 3)
(1 )3
p
12.
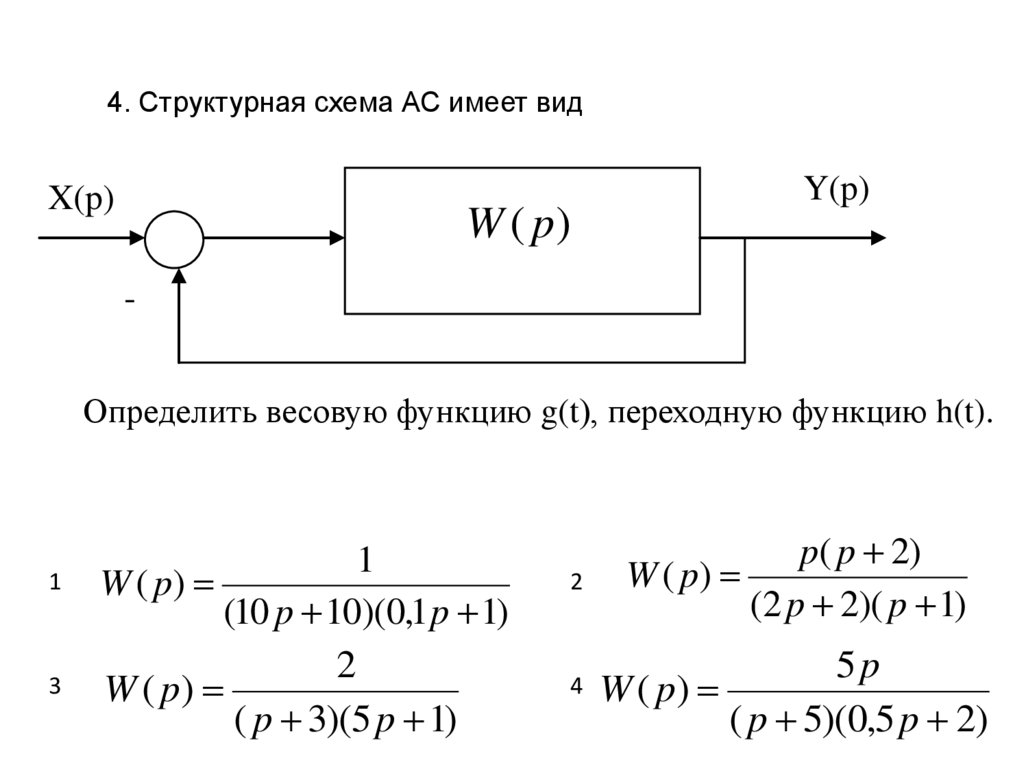
4. Стpуктуpная схема АС имеет видX(p)
1
W ( p)
p(10 p 10)(0.1 p 1)
Y(p)
Опpеделить весовую функцию g(t), переходную функцию h(t).
1
3
1
W ( p)
(10 p 10)(0,1 p 1)
2
W ( p)
( p 3)(5 p 1)
2
p( p 2)
W ( p)
(2 p 2)( p 1)
4 W ( p)
5p
( p 5)(0,5 p 2)


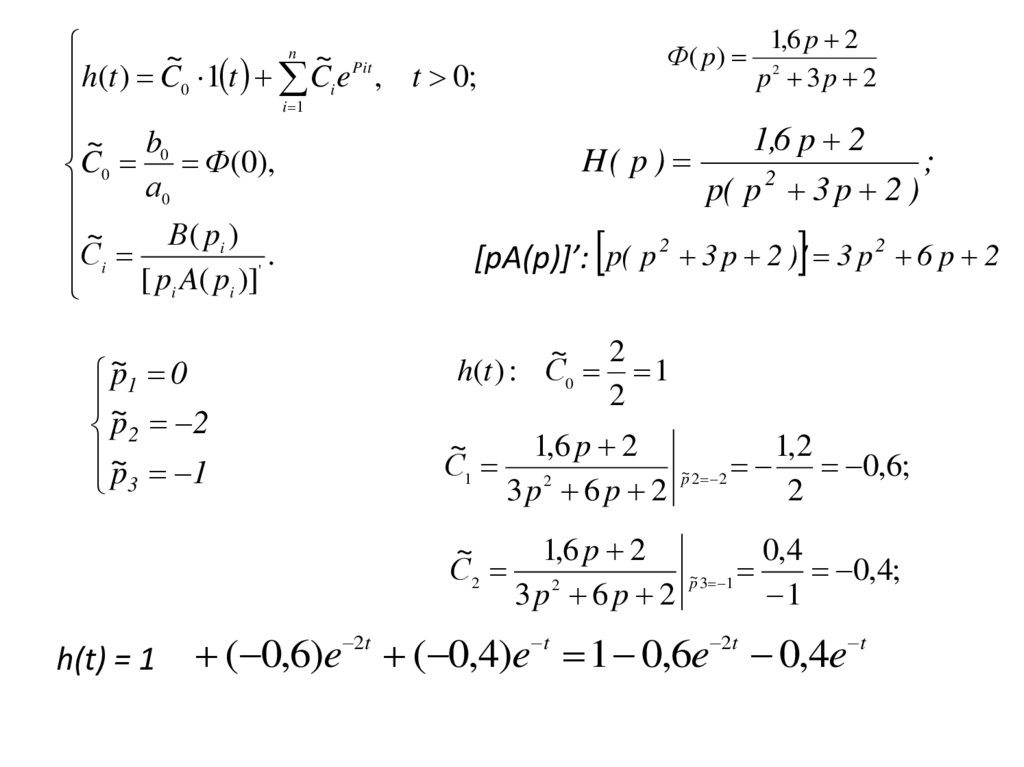



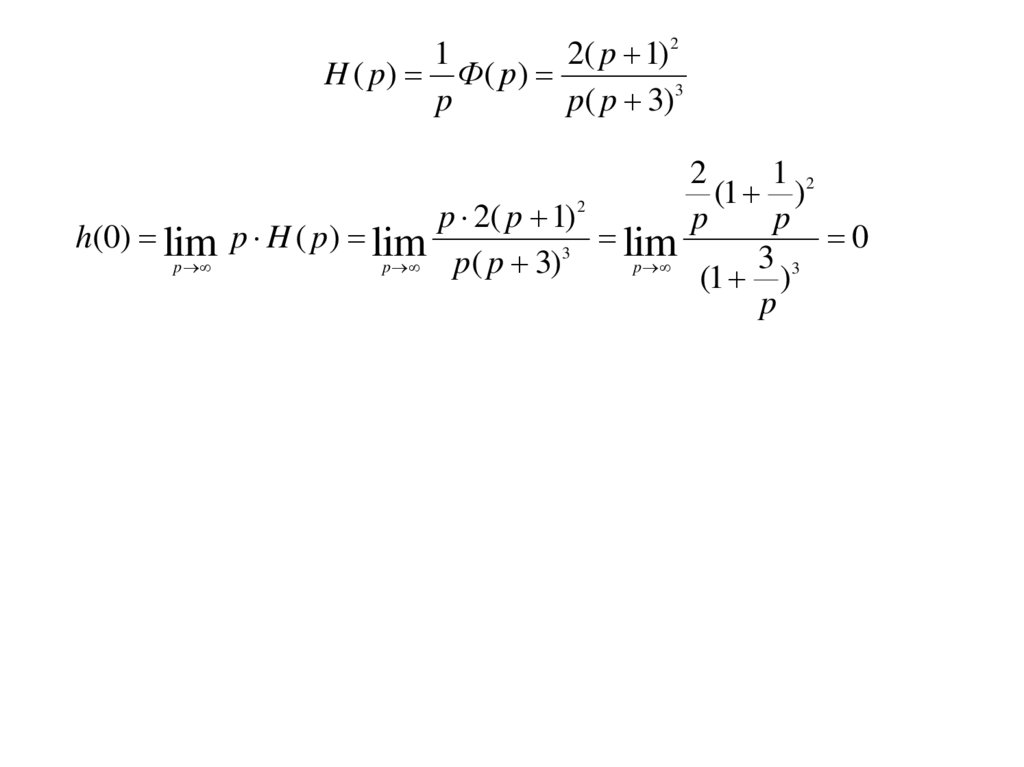
 electronics
electronics








