Similar presentations:
Трапеция
1.
2.
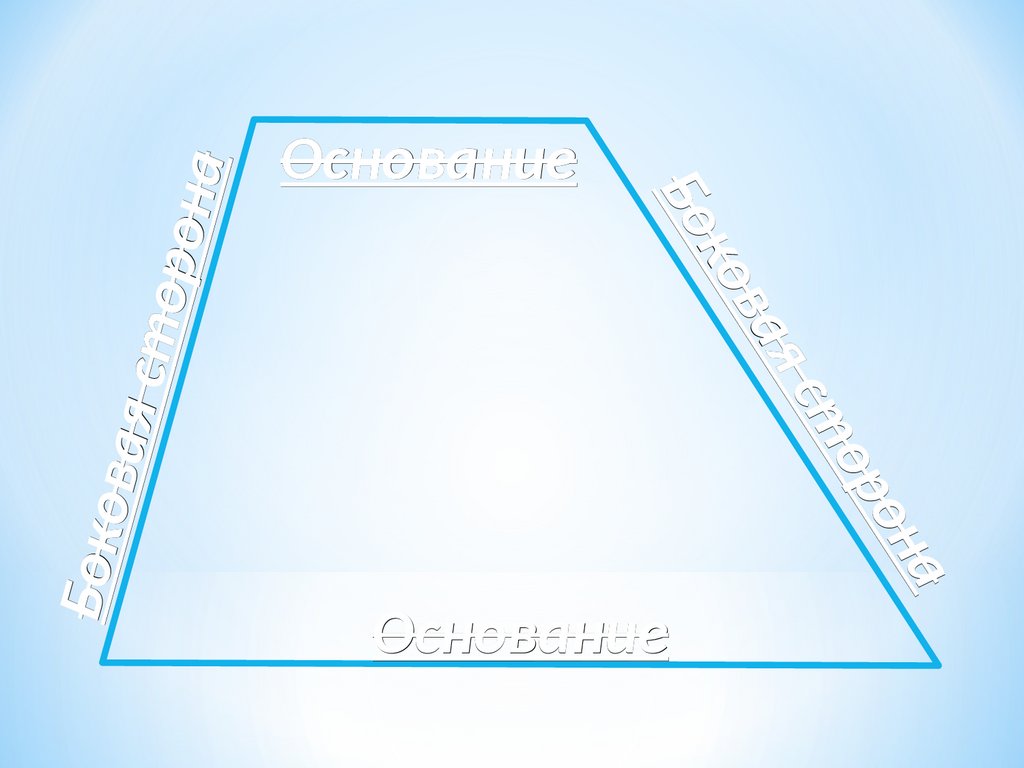
Трапецией называетсячетырёхугольник, у которого две
стороны параллельны, а две
другие стороны не параллельны
(Трапе́ ция от др.-греч. τραπέζιον—
«столик» от τράπεζα— «стол»)
3.
аон
ор
ст
Боко
ва я с
то р о
на
я
ва
ко
Бо
Основание
Основание
4.
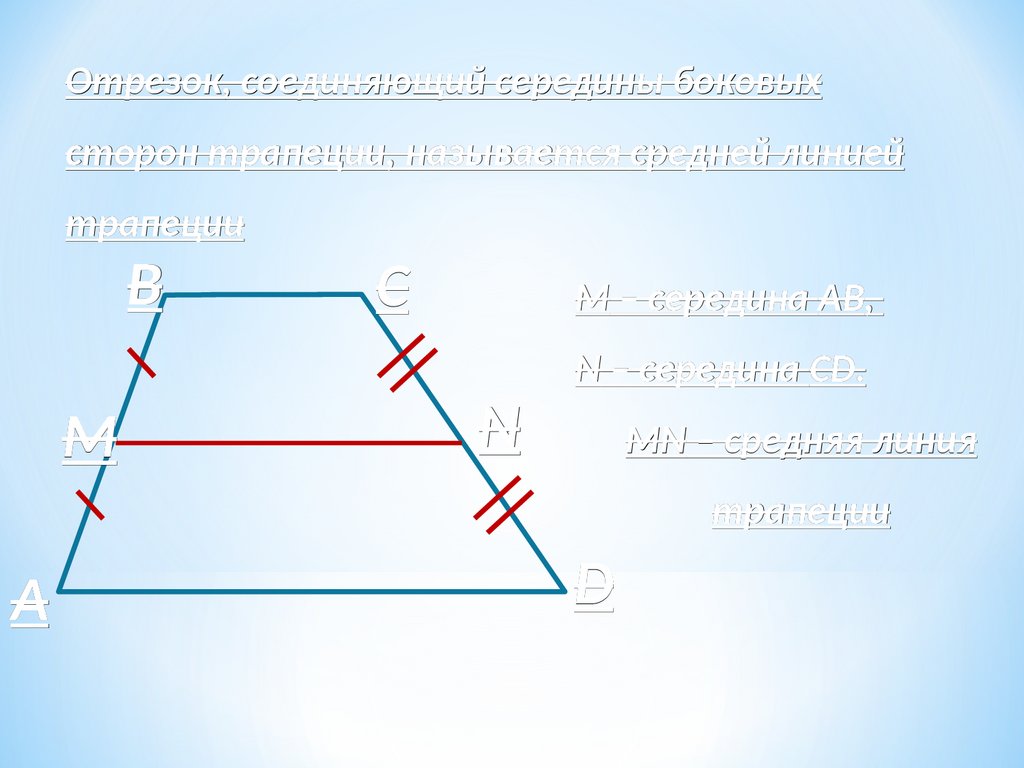
Отрезок, соединяющий середины боковыхсторон трапеции, называется средней линией
трапеции
B
M
C
M – середина АВ,
АВ,
N
N – середина CD.
MN – средняя линия
трапеции
A
D
5.
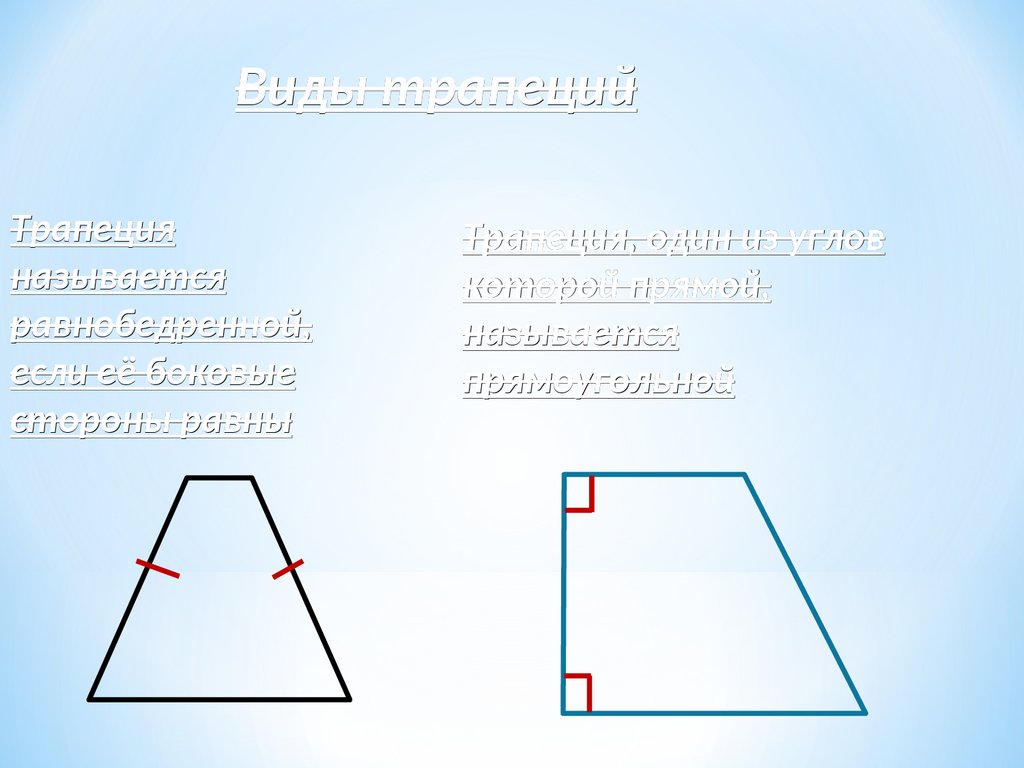
Виды трапецийТрапеция
называется
равнобедренной,
если её боковые
стороны равны
Трапеция, один из углов
которой прямой,
прямой,
называется
прямоугольной
6.
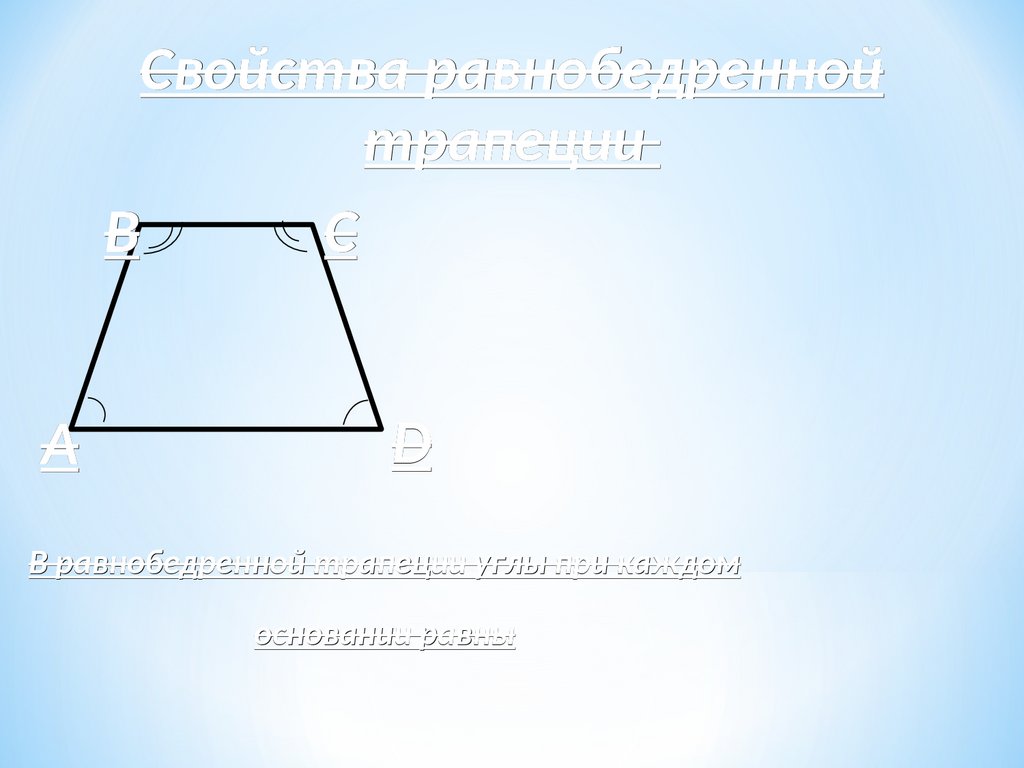
Свойства равнобедреннойтрапеции
B
C
A
D
В равнобедренной трапеции углы при каждом
основании равны
7.
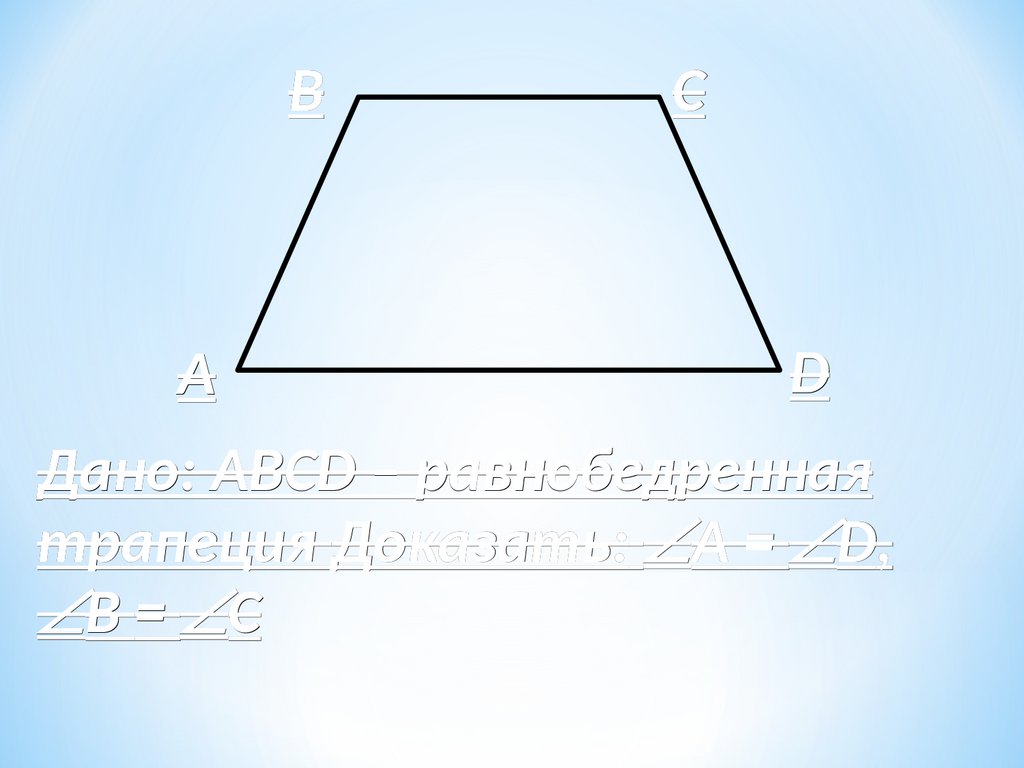
BA
C
D
Дано: ABCD – равнобедренная
трапеция Доказать: A = D,
B = C
8.
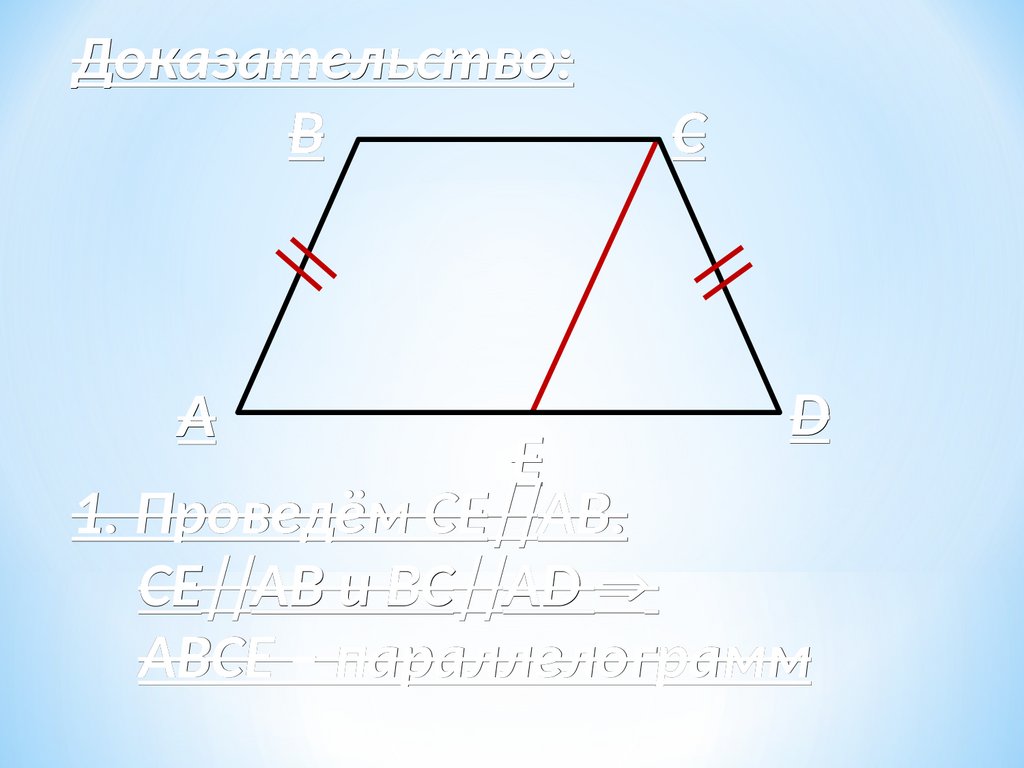
Доказательство:B
A
C
D
E
1. Проведём СЕ АВ.
СЕ АВ и ВС АD
ABCЕ – параллелограмм
9.
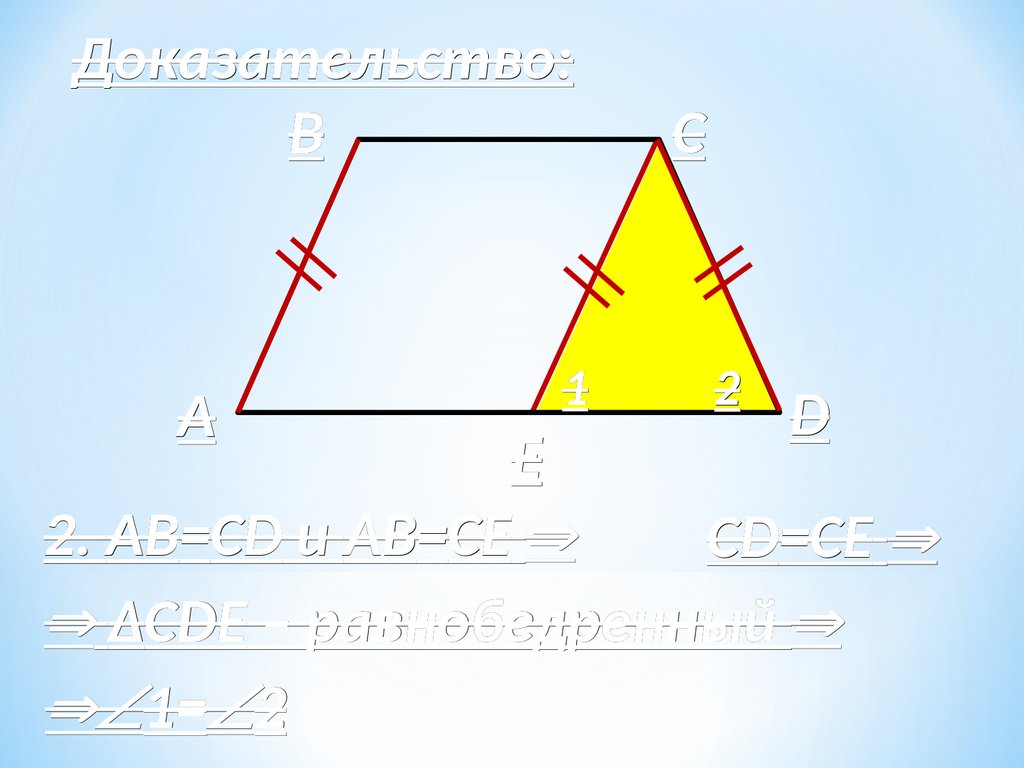
Доказательство:B
A
1
C
2
D
E
2. АВ=
АВ=CD и АВ=
АВ=СЕ
CD=
CD=СЕ
ΔCDЕ – равнобедренный
1= 2
10.
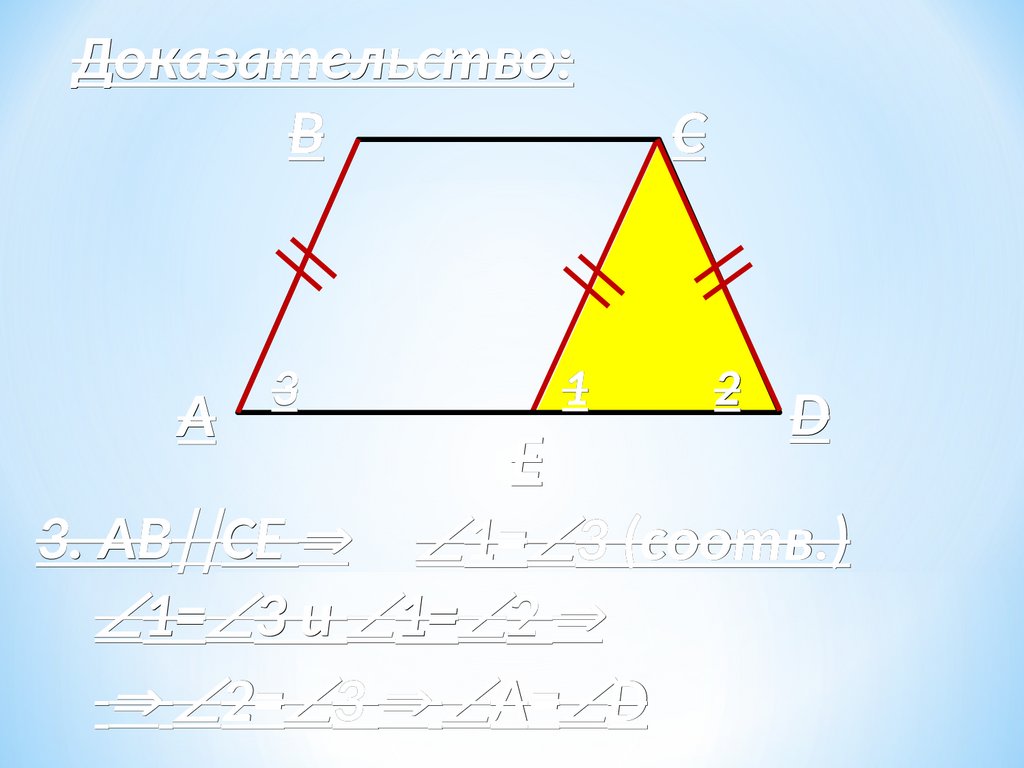
Доказательство:B
A
3
1
C
2
D
E
3. АВ CЕ 1= 3 (соотв.)
1= 3 и 1= 2
2= 3 А= D
11.
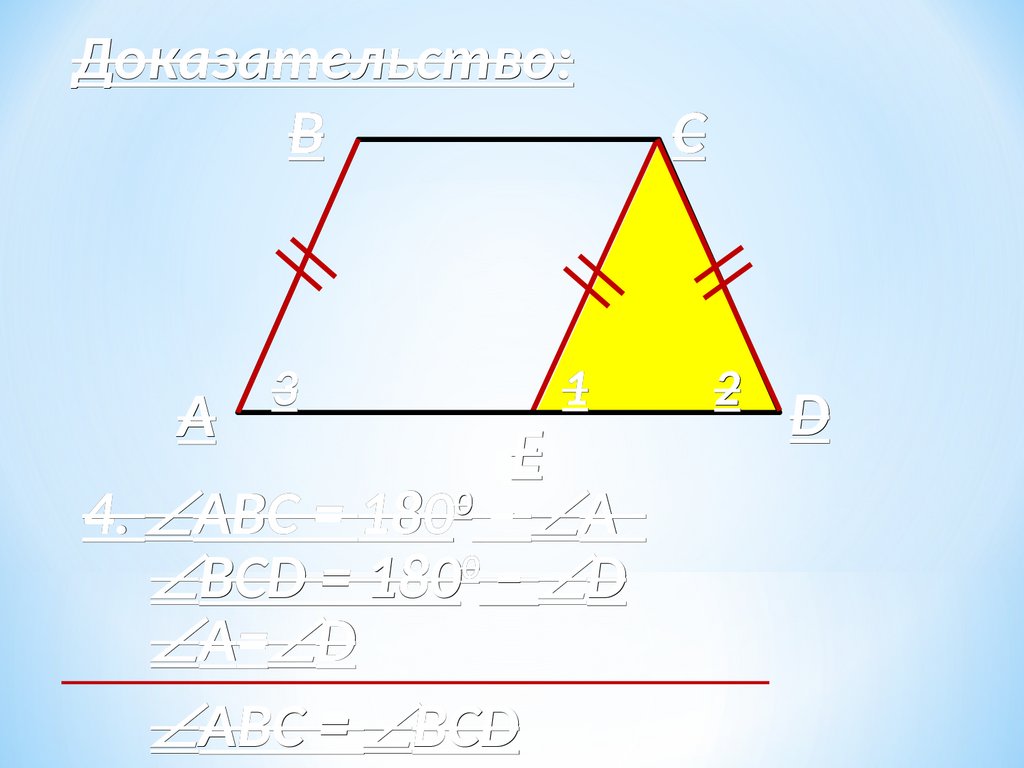
Доказательство:B
A
3
1
E
4. АВC = 1800 – А
0
ВCD = 180 – D
А= D
АВC = ВCD
C
2
D
12.
BA
C
D
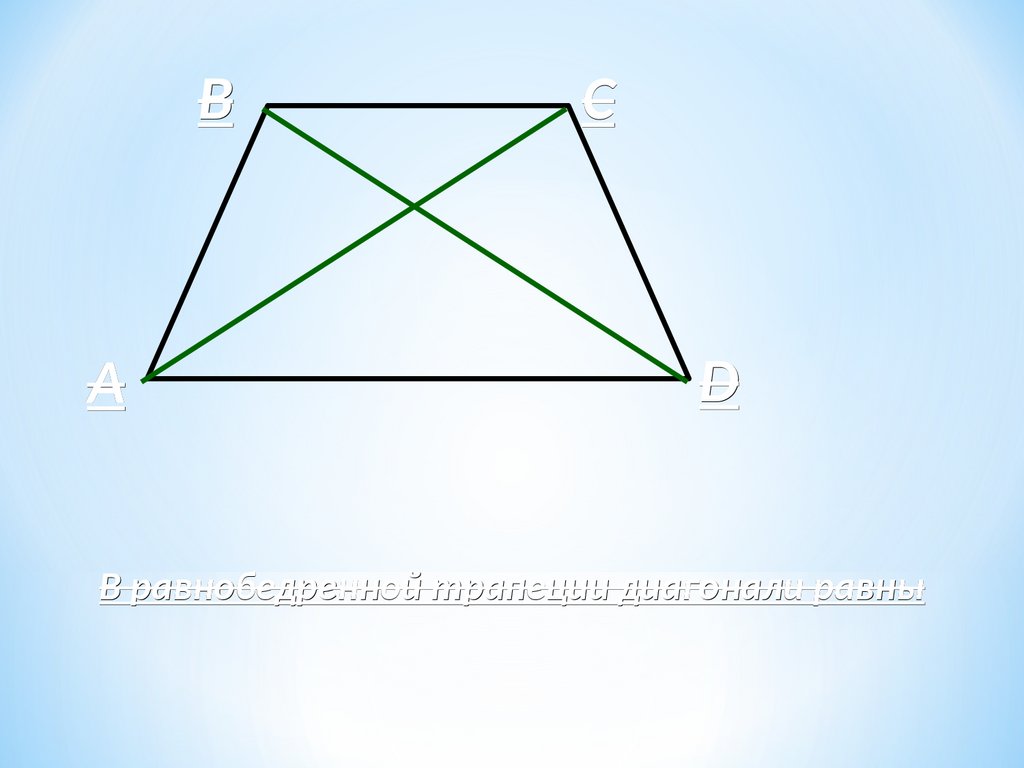
В равнобедренной трапеции диагонали равны
13.
BA
C
D
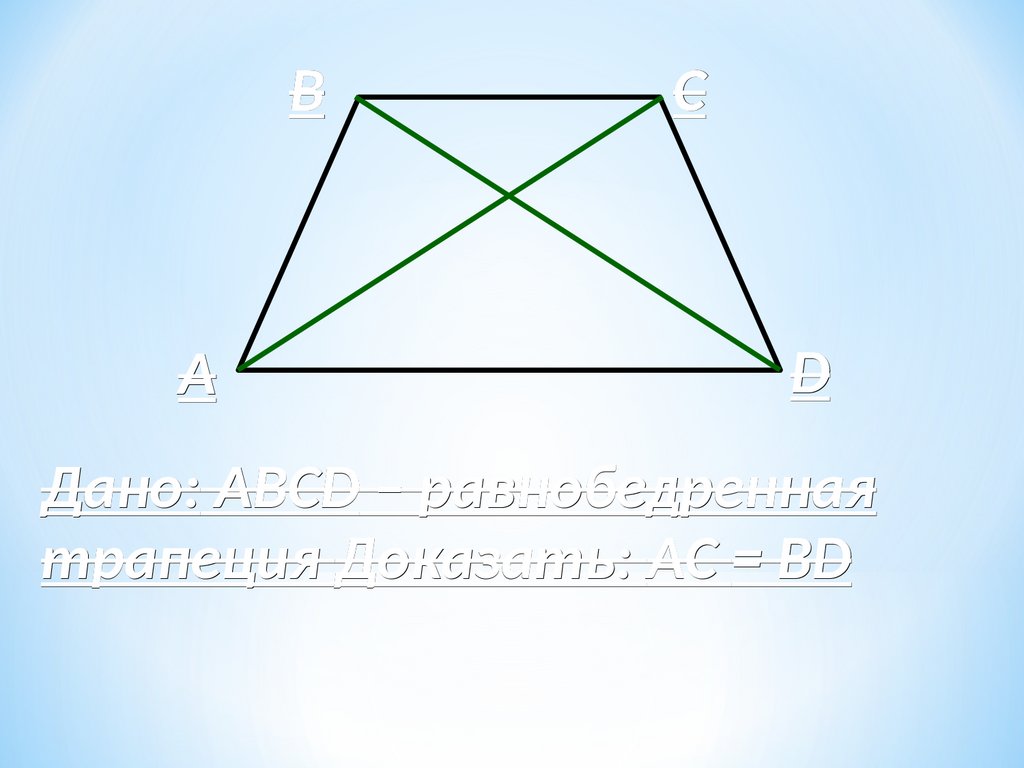
Дано: ABCD – равнобедренная
трапеция Доказать: АС = ВD
14.
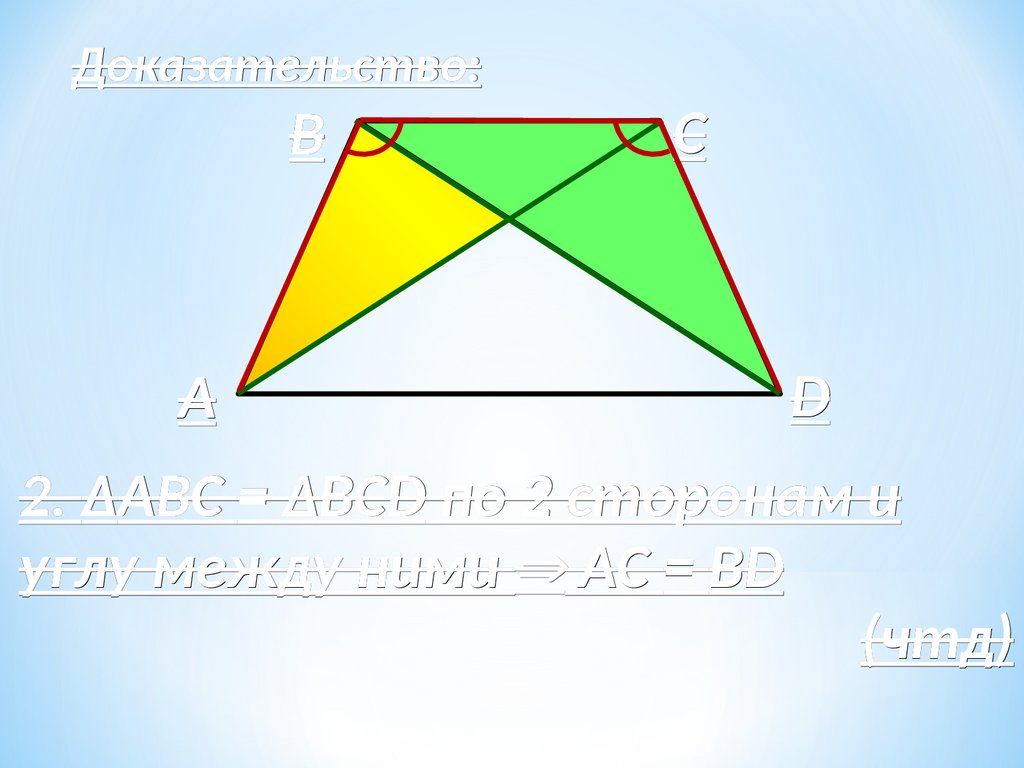
Доказательство:B
A
C
D
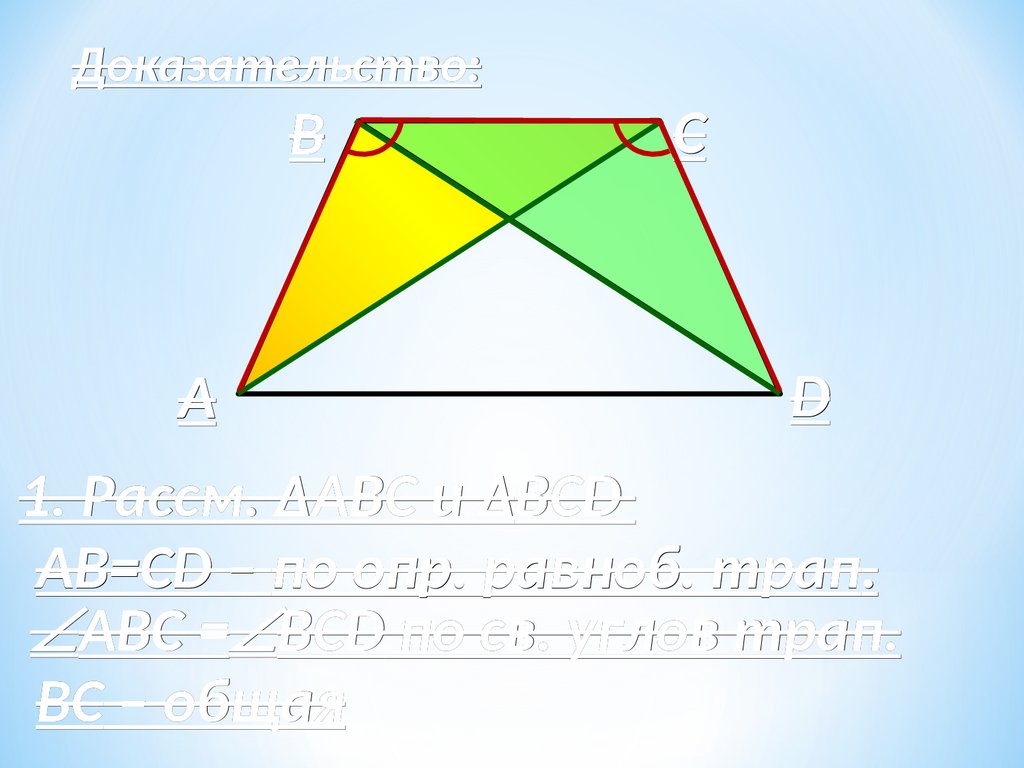
1. Рассм. ΔАВС
ΔАВС и ΔВCD
ΔВCD
АB=CD – по опр. равноб. трап.
трап.
АВС = BCD по св. углов трап.
ВС – общая
15.
Доказательство:B
A
C
D
2. ΔАВС = ΔВCD по 2 сторонам и
углу между ними АC = BD
(чтд)
16.
Свойства равнобедреннойтрапеции
1. В равнобедренной трапеции
углы при каждом основании
равны
2. В равнобедренной трапеции
диагонали равны
17.
Признаки равнобедреннойтрапеции
1. Если углы при каждом
основании трапеции равны,
то она равнобедренная
2. Если диагонали трапеции
равны, то она
равнобедренная
18.
Задача 1Найдите углы М и Р
трапеции MNPQ с
основаниями MQ и NP, если
N = 1090, а Q = 370
19.
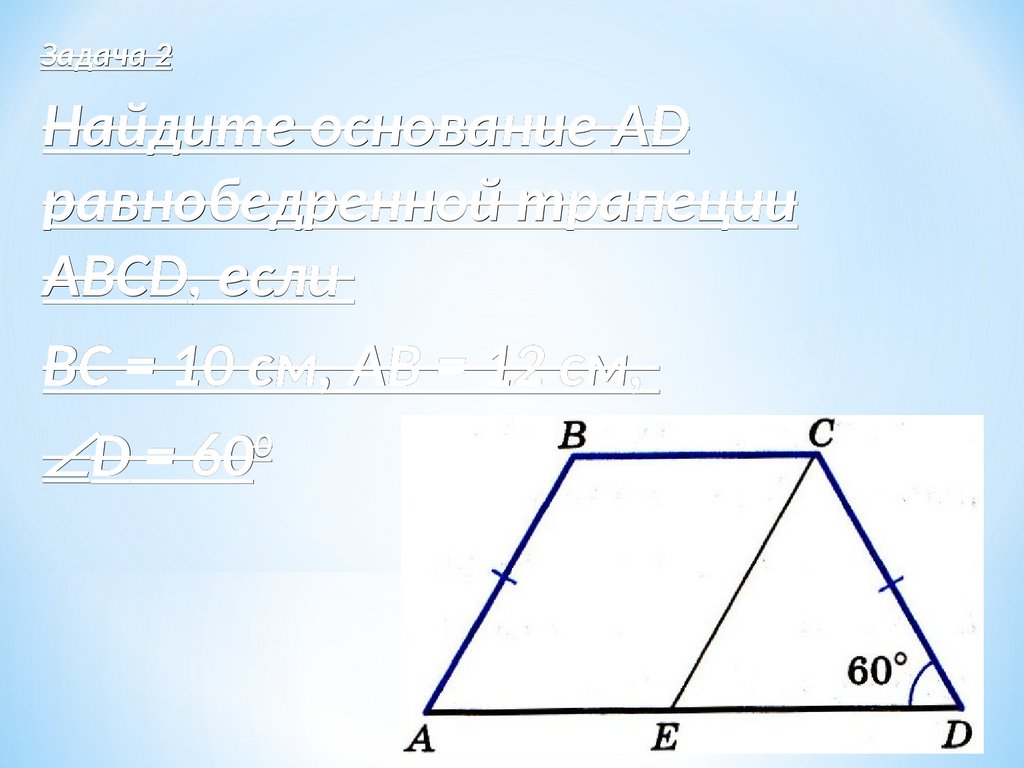
Задача 2Найдите основание AD
равнобедренной трапеции
ABCD,
ABCD, если
ВС = 10 см, АВ = 12 см,
D = 600
20.
Домашнее задание1. Определение, свойства и признаки
параллелограмма и трапеции
выучить
2. Решить задачи из учебника:
№ 387, № 390
21.
Список литературы1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Геометрия: Учебник для 7-9 кл. средней школы.
Москва, 2014 г.
2. Гаврилова Н.Ф. Поурочные разработки по
геометрии: 8 класс.– М.: ВАКО, 2010. (В помощь
школьному учителю).







 mathematics
mathematics








