Применение интегралов для решения физических задач

1. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ДЛЯ РЕШЕНИЯ ФИЗИЧЕСКИХ ЗАДАЧ

2.

b
S f ( x)dx F х ba F (b) F (a)
a

3.

Исаак Ньютон
(1643-1727)

4. Лейбниц Готфрид Вильгельм (1646-1716)

« Общее искусство знаков
представляет чудесное пособие,
так как оно разгружает
воображение… Следует
заботиться о том, чтобы
обозначения были удобны для
открытий. Обозначения коротко
выражают и отображают
сущность вещей. Тогда
поразительным образом
сокращается работа мысли.»
Лейбниц

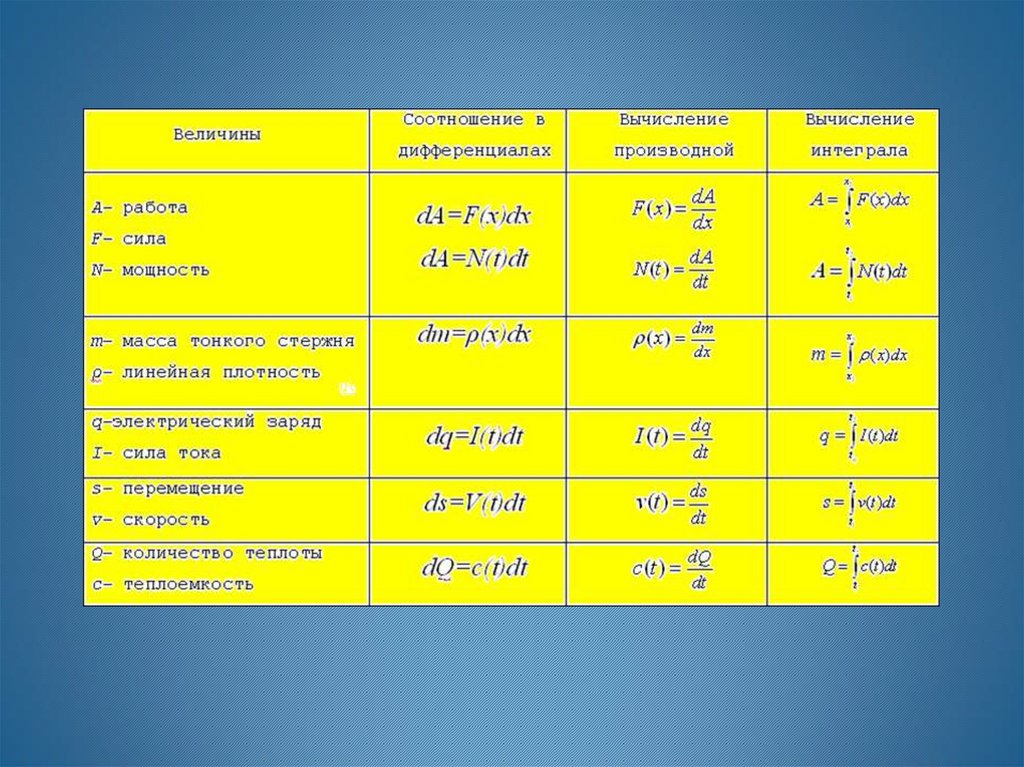
5. Физические приложения определенного интеграла

6. Схема решения физических задач с использованием определенного интеграла

А) сделать чертеж, соответствующий условию задачи,
Б) выбрать систему координат,
В) выбрать независимую переменную,
Г) выбрать формулу классической физики,
соответствующую условию задачи,
Д) найти дифференциал искомой величины на основании
этой формулы,
Е) установить промежуток интегрирования,
Ж) вычислить интеграл, т.е. найти искомую величину.

7.

8. Пример 1. Нахождение пути по заданной скорости.

Пусть точка движется со скоростью V(t). Нужно найти путь s, пройденный точкой от
момента t=a до момента t=b. Обозначим s(t) путь, пройденный точкой за время t от
момента a. Тогда s’(t)=V(t), т.е. s(t) – первообразная для функции V(t). Поэтому по
формуле Ньютона - Лейбница найдём:
s= V(t)dt.
Например, если точка движется со скоростью V(t)=2t+1(м/с), то путь, пройденный
точкой за первые 10 с, по формуле равен
10
2
10
S= ∫ (2t+1)dt = (t + t)| = 110(м)

9. Пример 2.Вычисление кинетической энергии

10. Пример 3.Нахождение силы.

11. Масса стержня

Пусть плотность ρ ( x ) стержня с
постоянным сечением S зависит от
расстояния до начала стержня. Тогда
масса стержня равна:
где L – длина стержня, а центр масс стержня
находится на расстоянии: