Similar presentations:
Комплексные числа. Изображение комплексных чисел на координатной плоскости. Тема 4
1.
Государственное бюджетное профессиональноеобразовательное учреждение города Москвы
«Московский колледж архитектуры и градостроительства»
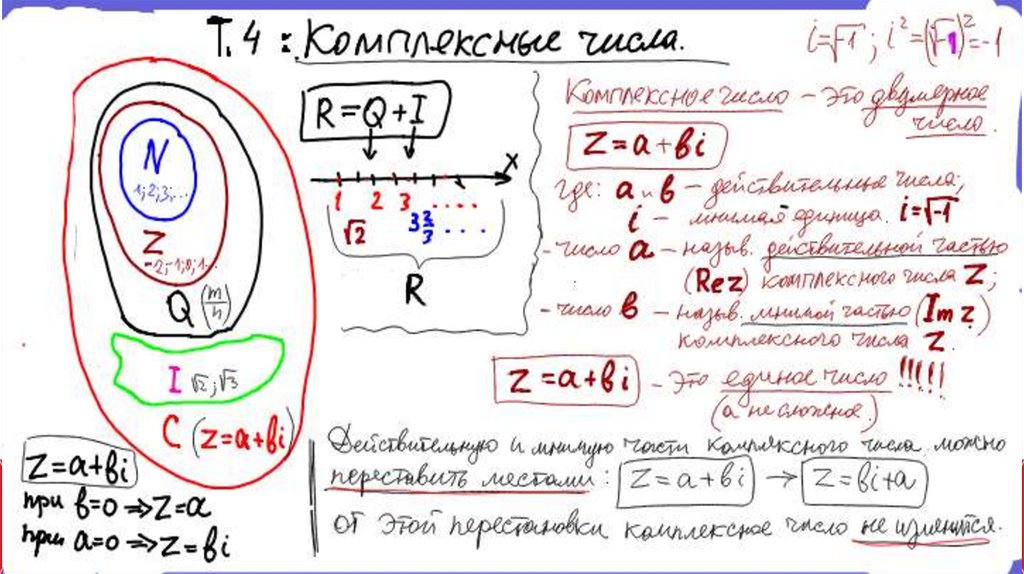
Тема-4: Комплексные числа. Изображение комплексных чисел
на координатной плоскости
Москва 2022 г.
2.
Историческая справкаПонятие комплексного числа возникло из практики и теории решения
алгебраических уравнений.
Вплоть до ХVI века математики всего мира комплексные корни,
возникавшие при решении квадратных уравнений, объявляли ложными и
не принимали их во внимание.
Смысл комплексных чисел
разъяснил
итальянский
математик
Рафаэль Бомбелли (1526-1572). В своей книге «Алгебра» (1572 г.) он
впервые изложил правила действий над комплексными числами в
современной форме.
Вместе с тем, вплоть до XVIII века, комплексные числа считались
«воображаемыми» и бесполезными.
Лишь в XVIII веке многие задачи математического анализа, геометрии,
механики требовали широкого применения операций над комплексными
числами, что создало условия для разработки их геометрического
истолкования.
3.
Большой вклад в исследование комплексных чиселвнесли немецкие математики: Леонард Эйлер (1707-1783),
который ввёл обозначение i для мнимой единицы ,
а также Карл Фридрих Гаусс (1777 -1855), который в
1831 году ввёл в науку термин «комплексное число».
Л. Эйлер
К. Гаусс
4.
5.
Геометрическая интерпретациякомплексного числа XVIII-XIX вв.
В начале XIX века К. Гаусс разработал геометрическую
интерпретацию, позволившую уяснить геометрический смысл
операций над комплексными числами.
Im z – (мнимая ось)
С
(комплексная плоскость)
М(a, b)
b
0
z = a + bi
a
Re z
(действительная ось)
К. Гаусс
(1777 -1855)
6.
Два комплексных числа: z1 = a1 + b1 i и z2 = a2 + b2 iназываются равными (z1 = z2 ) тогда и только тогда, когда
равны их действительные части и равны их мнимые части:
a1 = a2 и
b1 = b2 .
В частности, комплексное число z = a + b i = 0 равно нулю
тогда и только тогда, когда a = b = 0.
Понятие «больше» и «меньше» для комплексных чисел
не вводится!!!
7.
8.
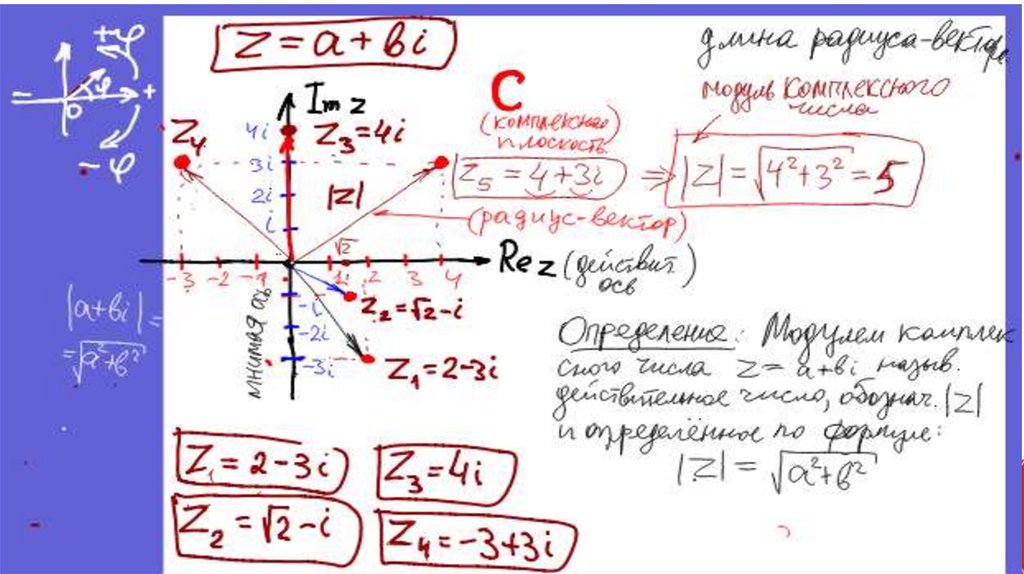
Модуль комплексного числа• Модулем комплексного числа z = a + bi
называется длина вектора | z |:
Im z (мнимая ось)
С
М (a, b)
zz
||
b
0
a
Re z
(действительная ось)
a 2 b2
9.
Пример-1: Найти модуль комплексного числа:z
|z|
a 2 b2
z1 2 i
z1
2 2 1
z 2 2 6 5i
z2
2 6 5 24 25 49 7
z3 i
z3
0 2 12
z 4 4
z4
4 2 0 2
2
2
4 1
2
1 1
16 4
5
10.
Аргумент комплексного числа• Аргументом комплексного числа называется угол ,
который образует вектор OM с положительным
направлением оси абсцисс: = arg z
Im z
М (a, b)
b
О
a
Re z
11.
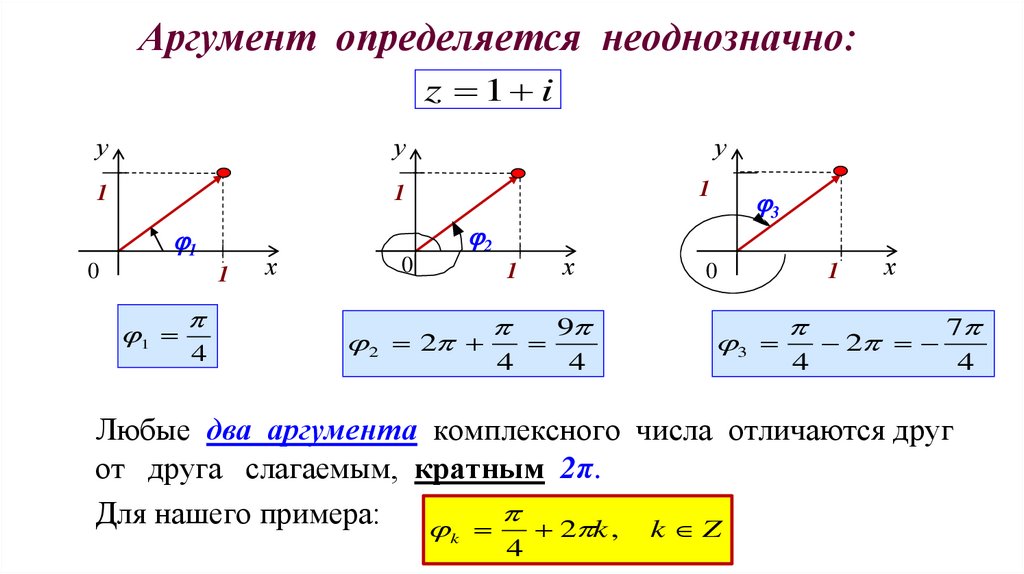
Аргумент определяется неоднозначно:z 1 i
у
у
1
1
1
0
1
1
4
х
у
1
2
0
1
2 2
4
3
х
0
9
4
3
1
4
х
2
7
4
Любые два аргумента комплексного числа отличаются друг
от друга слагаемым, кратным 2π.
Для нашего примера: 2 k , k Z
k
4
12.
Пример -2: Найти аргументы комплексного числа:z2 1
z1 i
Im z
arg z1
3
2 k , k Z
2
arg z2 0 2 k , k Z
Im z
0
Re z
-1
z3 1
Im z
-1
0
tan
tg
0
Re z
3
1
Re z
3 i
3
1
3
3
arg z3
3
4
3
4
2 k , k Z
3
13.
Пример – 3: Найти модуль и аргумент комплексного числа:3 i17
i18
z
Решение:
z
3 i17
i18
z
3 1 3 1 4 2
3 i
3 i
1
2
b
1
tan
tg
a
3
Im z
1
2
3
0
6
5
6
6
arg z
5
2 k , k Z
6
Re z
14.
Для комплексных чисел существуетнесколько форм записи:
- алгебраическая форма записи;
- тригонометрическая форма записи;
- показательная форма записи.
15.
Алгебраическая форма записикомплексного числа
16.
17.
18.
Пример - 4: Изобразить на комплексной плоскостиследующие числа:
Im z
z1 3 2 i
z 2 z1
2
z 3 z1
z 4 Re z1
-3
z5
z4
0
3
Re z
z 5 Im z1
-2
Два комплексных числа, отличающиеся только знаком мнимой части,
называются комплексно сопряженными:
z a i b, и z a i b,
19.
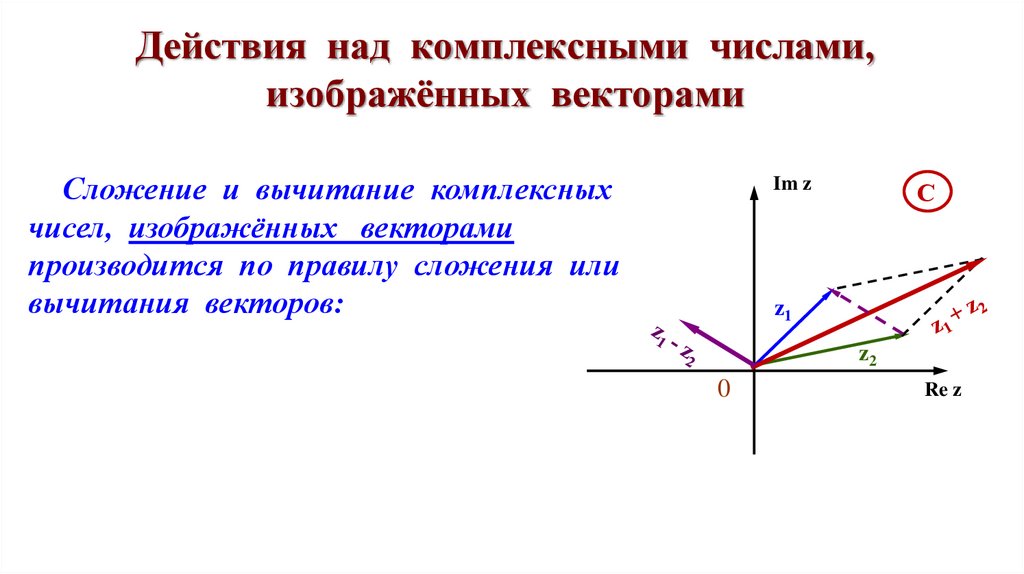
Действия над комплексными числами,изображённых векторами
Сложение и вычитание комплексных
чисел, изображённых векторами
производится по правилу сложения или
вычитания векторов:
Im z
С
z1
z2
0
Re z
20.
Тригонометрическая форма записикомплексного числа
21.
22.
23.
Пример – 3: Записать в тригонометрической формечисло:
z 2 2 3 i
z a bi r (cos i sin )
Решение:
r z
2 2 2 3
2
4 12
16 4
Im z
tg ∝ =
2 3
-2
Re z
2 3
=
|−2|
3
∝=
























 mathematics
mathematics








