Similar presentations:
Алгоритм. Свойства алгоритма
1.
Алгоритм. Свойства алгоритмаОднозначность алгоритма, под которой понимается единственность
толкования исполнителем правила построения действий и порядок их
выполнения. Чтобы алгоритм обладал этим свойством, он должен быть записан
командами из системы команд исполнителя.
Конечность алгоритма – обязательность завершения каждого из действий,
составляющих алгоритм, и завершимость выполнения алгоритма в целом.
Результативность алгоритма, предполагающая, что выполнение
алгоритма должно завершиться получением определённых результатов.
Массовость, т. е. возможность применения данного алгоритма для решения
целого класса задач, отвечающих общей постановке задачи. Для того чтобы
алгоритм обладал свойством массовости, следует составлять алгоритм,
используя обозначения величин и избегая конкретных значений.
Правильность алгоритма, под которой понимается способность алгоритма
давать правильные результаты решения поставленных задач.
Эффективность – для решения задачи должны использоваться
ограниченные ресурсы компьютера (процессорное время, объём оперативной
памяти и т. д.).
2.
Описание алгоритмов на естественном языке (Формульно-словесный).2, 3, +
1. Считать число a.
2. Считать число b.
3. Выполнить суммирование c := a + b.
4. Вывести число c.
а := а + 1
a=a+1
Пример 1. Cоставим алгоритм решения следующей задачи. Пусть заданы два
значения x и y. Необходимо сравнить эти значения и напечатать имя большей
переменной:
Ввести значение x.
Ввести значение y.
Если x < y, то напечатать «у», иначе напечатать «х».
3.
Пример 2. Найти y max( a, b, c). .Шаг 1. Положить y равным a .
Шаг 2. Если b y , то положить y равным b .
Шаг 3. Если c y , то положить y равным c . Конец.
Пример 3. Найти наибольший общий делитель двух целых чисел m n 0 .
Например, для m = 420 и n = 90 имеем
420 = 2 2 3 5 7; 90 = 2 3 3 5 .
Наибольший общий делитель в этом случае равен 2 3 5 = 30.
алгоритм Евклида.
d ( m, n ) . d ( m ,0 ) m .
Шаг 1. Если n = 0, то принять d m и закончить вычисления, иначе перейти к шагу 2.
Шаг 2. Вычислить q m / n и r m q n .
Шаг 3. Заменить значение m на n , а значение n - на значение r .
Перейти к шагу 1.
Здесь q - целая часть от деления m на n; r - остаток от деления.
4.
При m = 420, n = 90 имеем:Шаг 1. n = 90 0;
Шаг 2. q = [420/90] = 4; r = 420 - 4 90 = 60;
Шаг 3. m = 90; n = 60;
Шаг 1. n = 60 0;
Шаг 2. q = [90/60] = 1; r = 90 – 1 60 = 30;
Шаг 3. m = 60; n = 30;
Шаг 1. n = 30 0;
Шаг 2. q = [60/30] = 2; r = 60 – 2 30 = 0;
Шаг 3. m = 30; n = 0;
Шаг 1. n = 0 d = 30 .
5.
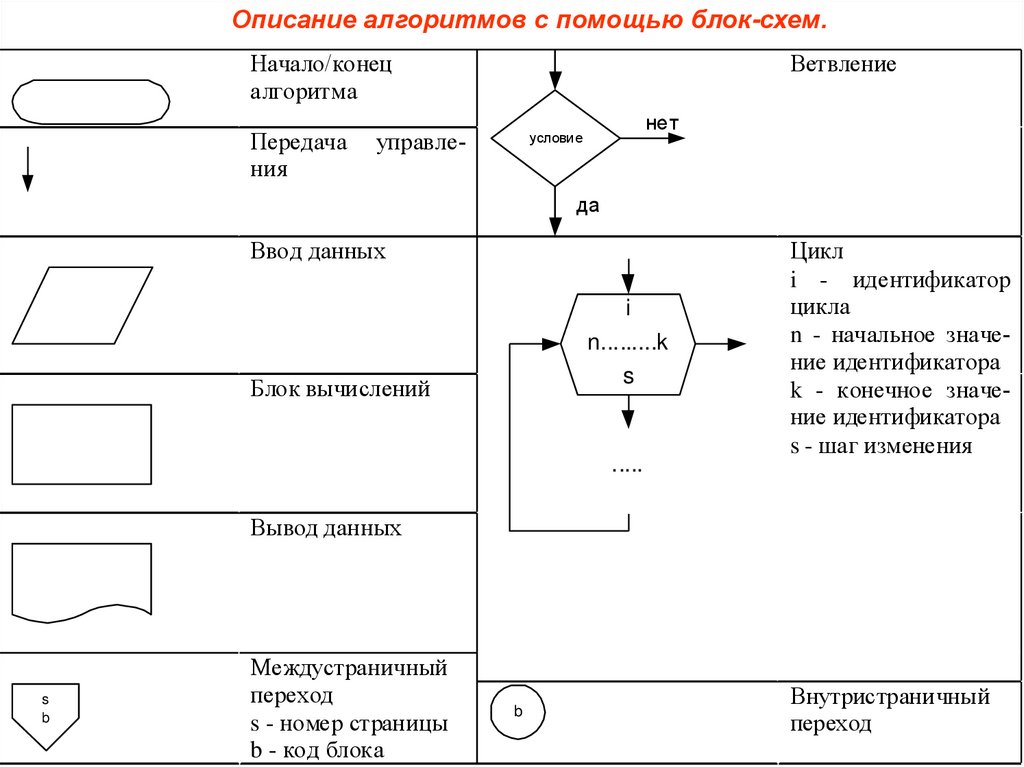
Описание алгоритмов с помощью блок-схем.Начало/конец
алгоритма
Передача
ния
Ветвление
управле-
нет
условие
да
Ввод данных
i
n.........k
s
Блок вычислений
.....
Цикл
i - идентификатор
цикла
n - начальное значение идентификатора
k - конечное значение идентификатора
s - шаг изменения
Вывод данных
s
b
Междустраничный
переход
s - номер страницы
b - код блока
b
Внутристраничный
переход
6.
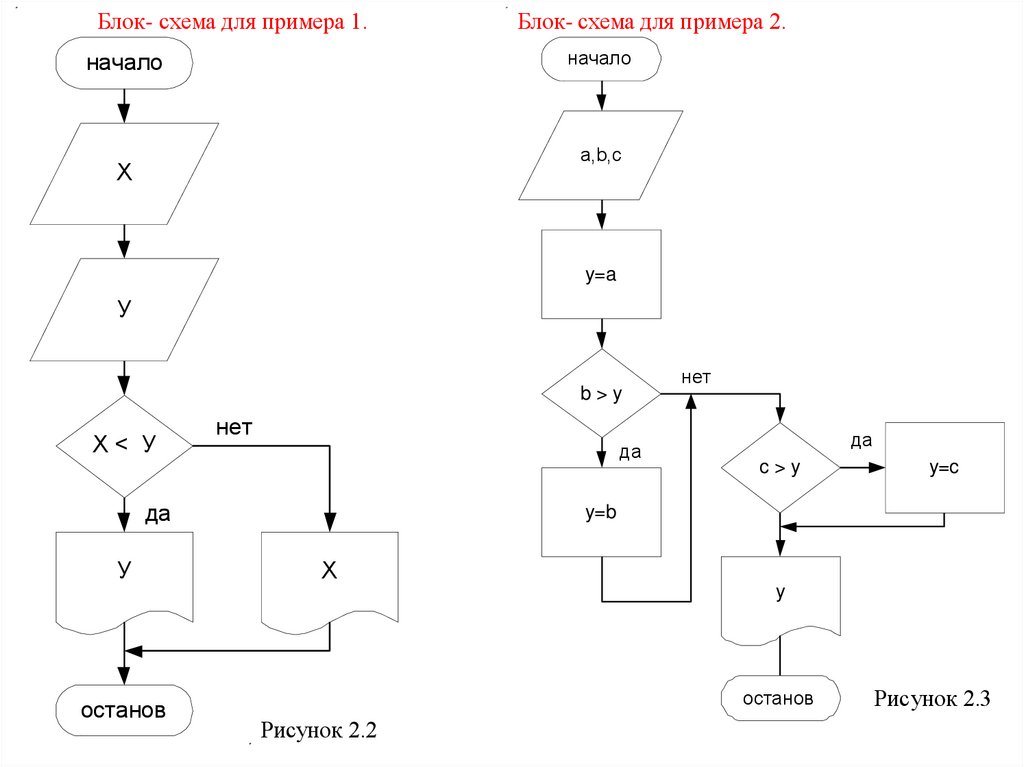
Блок- схема для примера 1.Блок- схема для примера 2.
начало
начало
а,b,c
Х
y=a
У
b>y
Х< У
нет
да
да
У
нет
да
c>y
y=c
y=b
Х
y
останов
останов
Рисунок 2.2
Рисунок 2.3
7.
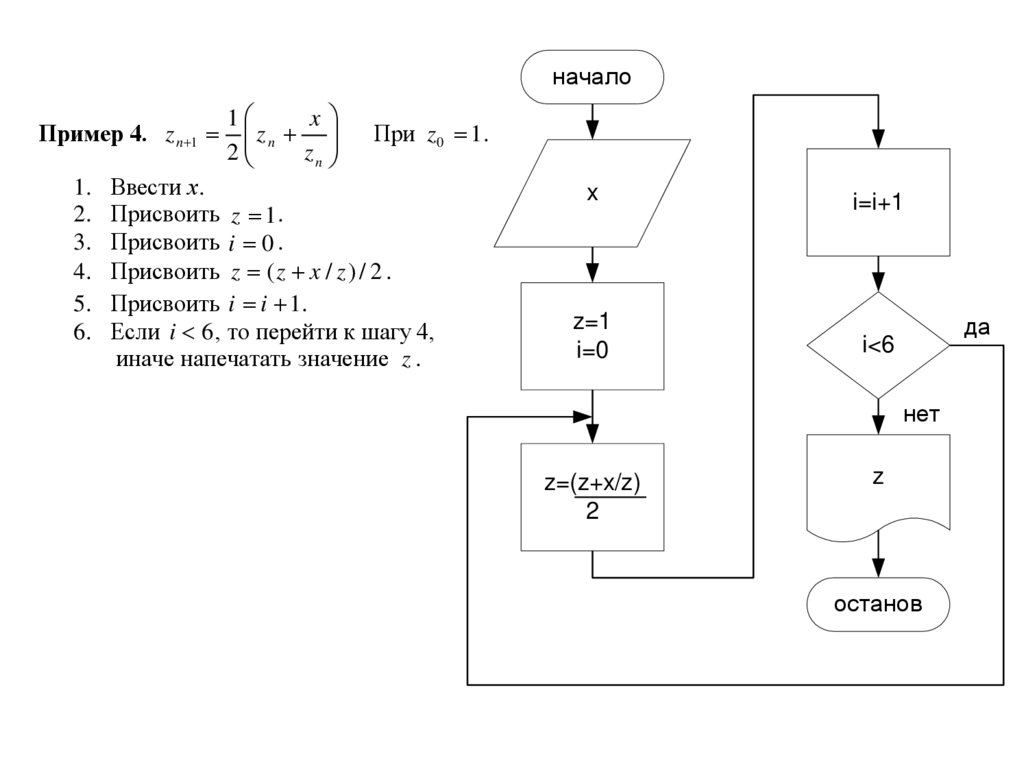
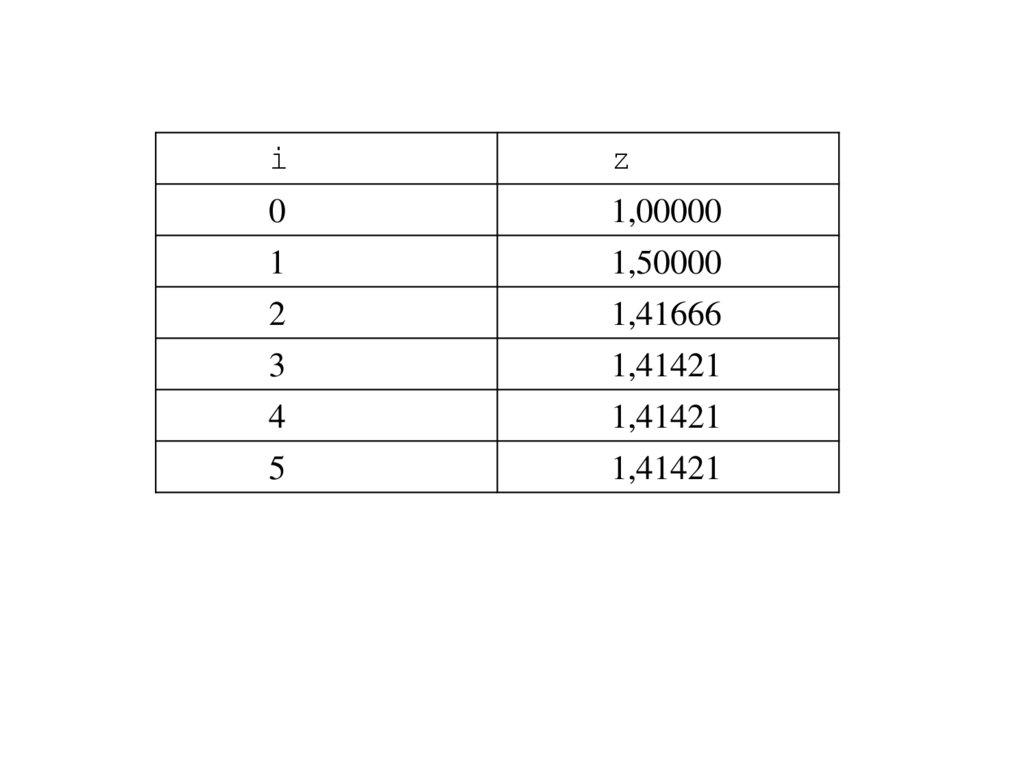
началоПример 4. z n 1
1.
2.
3.
4.
5.
6.
1
x
z n
2
zn
При z 0 1 .
Ввести х.
Присвоить z 1.
Присвоить i 0 .
Присвоить z ( z x / z ) / 2 .
Присвоить i i 1.
Если i 6 , то перейти к шагу 4,
иначе напечатать значение z .
x
z=1
i=0
i=i+1
да
i<6
нет
z=(z+x/z)
2
z
останов
8.
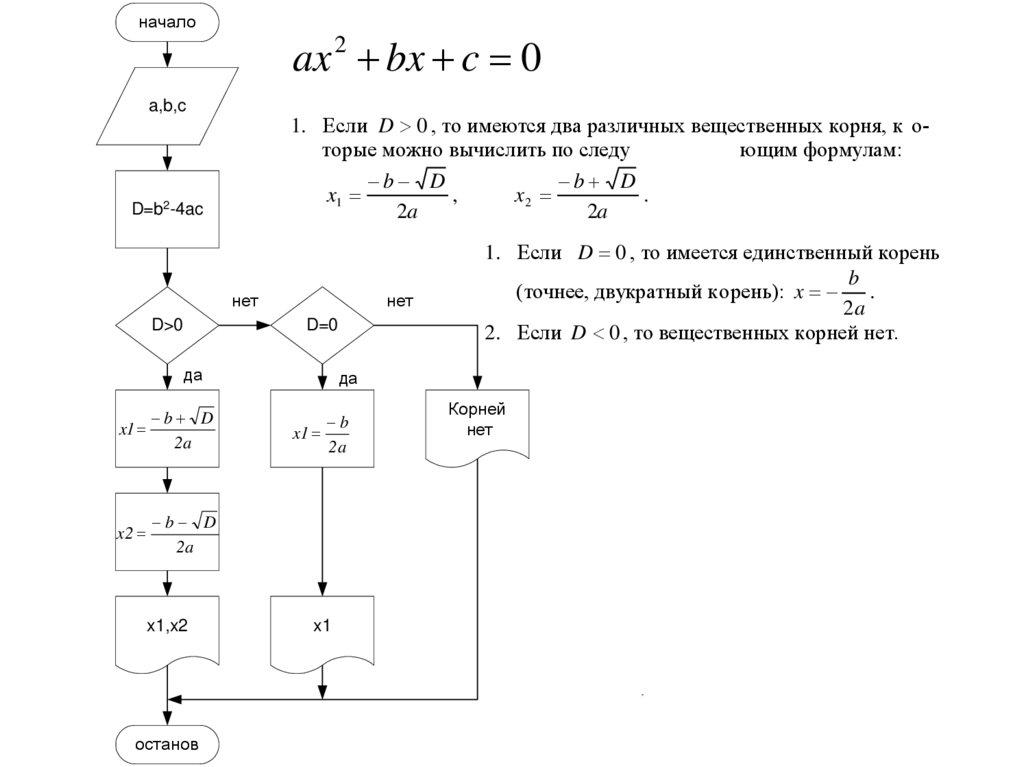
началоax 2 bx c 0
a,b,c
1. Если D 0 , то имеются два различных вещественных корня, к оторые можно вычислить по следу
ющим формулам:
b D
b D
x1
,
x2
.
2a
2a
D=b2-4ac
нет
D>0
нет
D=0
да
да
x1
b D
2a
b
x1
2a
x2
b D
2a
x1,x2
останов
x1
1. Если D 0 , то имеется единственный корень
b
(точнее, двукратный корень): x .
2a
2. Если D 0 , то вещественных корней нет.
Корней
нет
9.
началоa,b,c
да
a=0
b=0
нет
нет
c
x1
b
D=b2-4ac
да
c=0
да
нет
Корней
нет
Кореньлюбое
число
x1
Комплексные
корни
да
D<0
нет
да
D=0
b
2a
x1
b D
2a
x1,x2
x1
нет
x1
b D
2a
x2
останов
10.
iz
0
1
2
1,00000
1,50000
1,41666
3
4
5
1,41421
1,41421
1,41421





 mathematics
mathematics








